每日c/c++题 备战蓝桥杯(P2241 统计方形(数据加强版))
洛谷P2241 统计方形(数据加强版)题解
题目描述
给定一个 n × m n \times m n×m 的方格棋盘,要求统计其中包含的正方形数量和长方形数量(不包含正方形)。输入为两个正整数 n n n 和 m m m,输出两个整数分别表示正方形和长方形的数量。
输入输出样例
输入:
2 3
输出:
8 10
解题思路
方法一:枚举右下角坐标
核心思想:固定右下角坐标 ( i , j ) (i,j) (i,j),统计以该点为右下角的正方形和矩形数量。
-
正方形数量:
- 以 ( i , j ) (i,j) (i,j) 为右下角的正方形边长最大为 min ( i , j ) \min(i,j) min(i,j)。
- 例如,当 i = 2 , j = 3 i=2, j=3 i=2,j=3 时,最大边长为 2 2 2,可形成 2 2 2 个正方形(边长为 1 1 1 和 2 2 2)。
-
矩形数量:
- 以 ( i , j ) (i,j) (i,j) 为右下角的矩形数量为 i × j i \times j i×j(长为 i i i,宽为 j j j 的矩形)。
-
累加结果:
- 遍历所有右下角坐标 ( i , j ) (i,j) (i,j),累加正方形和矩形数量。
- 长方形数量 = 矩形总数 - 正方形总数。
代码实现:
#include <bits/stdc++.h>
using namespace std;int main() {long long n, m;cin >> n >> m;long long square = 0, rectangle = 0;for (int i = 1; i <= n; ++i) {for (int j = 1; j <= m; ++j) {square += min(i, j); // 累加正方形rectangle += i * j; // 累加矩形}}cout << square << " " << rectangle - square << endl;return 0;
}
方法二:数学公式法
核心思想:通过数学公式直接计算正方形和矩形总数。
-
正方形总数:
- 边长为 k k k 的正方形数量为 ( n − k + 1 ) × ( m − k + 1 ) (n-k+1) \times (m-k+1) (n−k+1)×(m−k+1)。
- 遍历 k k k 从 1 1 1 到 min ( n , m ) \min(n,m) min(n,m),累加所有可能边长的正方形数量:
square_total = ∑ k = 1 min ( n , m ) ( n − k + 1 ) ( m − k + 1 ) \text{square\_total} = \sum_{k=1}^{\min(n,m)} (n-k+1)(m-k+1) square_total=k=1∑min(n,m)(n−k+1)(m−k+1)
-
矩形总数:
- 从 n + 1 n+1 n+1 条横线中选 2 2 2 条,从 m + 1 m+1 m+1 条竖线中选 2 2 2 条,组合数为:
rectangle_total = n ( n + 1 ) 2 × m ( m + 1 ) 2 \text{rectangle\_total} = \frac{n(n+1)}{2} \times \frac{m(m+1)}{2} rectangle_total=2n(n+1)×2m(m+1)
- 从 n + 1 n+1 n+1 条横线中选 2 2 2 条,从 m + 1 m+1 m+1 条竖线中选 2 2 2 条,组合数为:
-
长方形数量:
- 长方形数量 = 矩形总数 - 正方形总数。
代码实现:
#include <bits/stdc++.h>
using namespace std;int main() {long long n, m;cin >> n >> m;long long square_total = 0, rectangle_total;// 计算正方形总数for (long long k = 1; k <= min(n, m); ++k) {square_total += (n - k + 1) * (m - k + 1);}// 计算矩形总数rectangle_total = (n * (n + 1) / 2) * (m * (m + 1) / 2);cout << square_total << " " << rectangle_total - square_total << endl;return 0;
}
复杂度分析
- 枚举法:时间复杂度为 O ( n × m ) O(n \times m) O(n×m),适用于 n , m ≤ 5000 n,m \leq 5000 n,m≤5000 的数据范围。
- 数学公式法:时间复杂度为 O ( min ( n , m ) ) O(\min(n,m)) O(min(n,m)),效率更高,适合处理更大规模的数据。
注意事项
- 数据类型:由于结果可能非常大,需使用
long long类型防止溢出。 - 输入范围:题目中 n n n 和 m m m 的范围为 1 ≤ n , m ≤ 5000 1 \leq n,m \leq 5000 1≤n,m≤5000,需确保代码能处理大数运算。
总结
本题可通过枚举法或数学公式法解决。枚举法直观易懂,适合初学者;数学公式法效率更高,适合处理大规模数据。实际编码中可根据需求选择合适的方法。
相关文章:
))
每日c/c++题 备战蓝桥杯(P2241 统计方形(数据加强版))
洛谷P2241 统计方形(数据加强版)题解 题目描述 给定一个 n m n \times m nm 的方格棋盘,要求统计其中包含的正方形数量和长方形数量(不包含正方形)。输入为两个正整数 n n n 和 m m m,输出两个整数分…...

Ota++框架学习
一:框架结构 这是一幅展现 Web 应用程序架构的示意图,以下是对图中各部分的详细解释: 外部交互部分 Request(请求):位于架构图的左上角,用黄色虚线框表示 。代表来自客户端(如浏览器…...

Chrome安装最新vue-devtool插件
本vue-devtool版本是官方的 v7.6.8版本,兼容性好、功能齐全且稳定。 操作步骤: 方法一: 打开谷歌浏览器 --> 右上角三个点 --> 扩展程序 --> 管理扩展程序 --> 加载已解压的扩展程序, 然后选择解压后的文件夹即可。…...

Android锁
引言 🔒 在 Android 应用的开发过程中,随着业务需求的复杂度不断提升,多线程并发场景层出不穷。为了保证数据一致性与线程安全,锁(Lock)成为了不可或缺的工具。本篇博客将深入剖析 Android 中常用的锁机制…...

bfs-最小步数问题
最小步长模型 特征: 主要是解决权值为1且状态为字符串类型的最短路问题,实质上是有向图的最短路问题,可以简化为bfs求最短路问题。 代表题目: acwing 845 八数码问题: 八数码题中由于每次交换的状态是由x进行上下左右…...

sqlalchemy库详细使用
SQLAlchemy 是 Python 中最强大、最受欢迎的 ORM(对象关系映射)库,它允许你使用 Python 对象来操作数据库,而不需要直接编写 SQL 语句。同时,它也提供了对底层 SQL 的完全控制能力,适用于从简单脚本到大型企…...
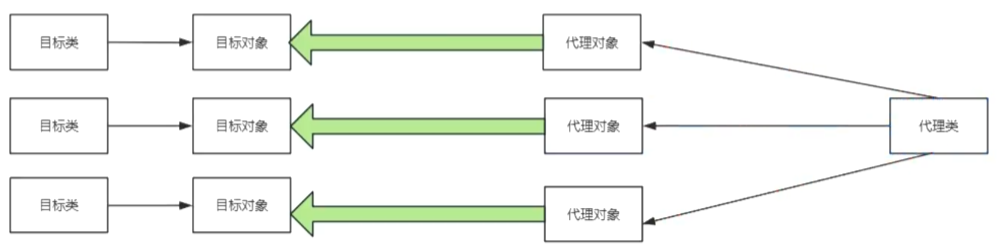
java----------->代理模式
目录 什么是代理模式? 为什么会有代理模式? 怎么写代理模式? 实现代理模式总共需要三步: 什么是代理模式? 代理模式:给目标对象提供一个代理对象,并且由代理对象控制目标对象的引用 代理就是…...
 分析)
ET ProcessInnerSender类(实体) 分析
ProcessInnerSender 作用是进程内部发送Actor消息 字段 TIMEOUT_TIME 超时时间RpcId 用来累加requestCallback 存储RPC的回调事件list 用来获取MessageQueue中的Actor消息 方法 Awake 初始化在MessageQueue中注册待处理的消息队列Destroy 移除在MessageQueue中的消息队列U…...

Untiy基础学习(十四)核心系统—物理系统之碰撞检测代码篇 刚体,碰撞体,材质
目录 一、碰撞器(Collider)与触发器(Trigger) 二、碰撞检测条件 三、碰撞事件与触发器事件,可以理解为特殊的生命周期函数。 四、讲讲如何选择 编辑 五、总结 一、碰撞/触发事件函数对照表 二、Collider 与 …...

SAP学习笔记 - 开发08 - Eclipse连接到 BTP Cockpit实例
有关BTP,之前学了一点儿,今天继续学习。 SAP学习笔记 - 开发02 - BTP实操流程(账号注册,BTP控制台,BTP集成开发环境搭建)_sap btp开发-CSDN博客 如何在Eclipse中连接BTP Cockpit开发环境实例。 1…...

如何用Redis实现分布式锁?RedLock算法的核心思想?Redisson的看门狗机制原理?
一、Redis分布式锁基础实现 public class RedisDistributedLock {private JedisPool jedisPool;private String lockKey;private String clientId;private int expireTime 30; // 默认30秒public boolean tryLock() {try (Jedis jedis jedisPool.getResource()) {// NX表示不…...

Java项目层级介绍 java 层级 层次
java 层级 层次 实体层 控制器层 数据连接层 Service : 业务处理类 Repository :数据库访问类 Java项目层级介绍 https://blog.csdn.net/m0_67574906/article/details/145811846 在Java项目中,层级结构(Layered Architecture…...
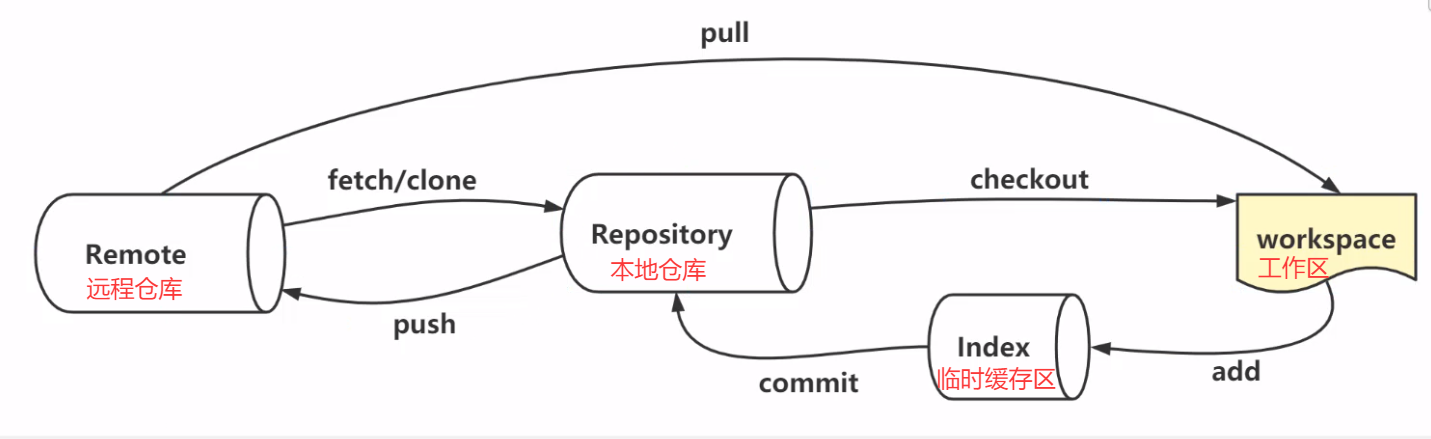
Git的安装和配置(idea中配置Git)
一、Git的下载和安装 前提条件:IntelliJ IDEA 版本是2023.3 ,那么配置 Git 时推荐使用 Git 2.40.x 或更高版本 下载地址:CNPM Binaries Mirror 操作:打开链接 → 滚动到页面底部 → 选择2.40.x或更高版本的 .exe 文件…...

【2025版】Spring Boot面试题
文章目录 1. Spring, Spring MVC, SpringBoot是什么关系?2. 谈一谈对Spring IoC的理解3. Component 和 Bean 的区别?4. Autowired 和 Resource 的区别?5. 注入Bean的方法有哪些?6. 为什么Spring 官方推荐构造函数注入?…...

火山引擎实时音视频 高代码跑通日志
实时音视频 SDK 概览--实时音视频-火山引擎 什么是实时音视频 火山引擎实时音视频(Volcengine Real Time Communication,veRTC)提供全球范围内高可靠、高并发、低延时的实时音视频通信能力,实现多种类型的实时交流和互动。 通…...

atoi函数,sprintf函数,memcmp函数,strchar函数的具体原型,功能,返回值;以及使用方法
以下是这四个C语言标准库函数的详细说明: 1. atoi() - 字符串转整数 **原型**: int atoi(const char *str); **功能**: 将字符串参数str转换为整数(int类型)。函数会跳过前面的空白字符(如空格、制表符&am…...

C++学习之打车软件git版本控制
目录 01 3-git的简介 02 4-git的下载和提交代码 03 5-git添加一个新文件 04 5-删除一个文件 05 6-git的批量添加和提交文件 06 7-git重命名文件名 07 8-git解决代码冲突 08 9-git的分支的概念 09 10-创建项目代码仓库 10 1-git提交代码复习 01 3-git的简介 1 --------…...

基于 PostgreSQL 的 ABP vNext + ShardingCore 分库分表实战
🚀 基于 PostgreSQL 的 ABP vNext ShardingCore 分库分表实战 📑 目录 🚀 基于 PostgreSQL 的 ABP vNext ShardingCore 分库分表实战✨ 背景介绍🧱 技术选型🛠️ 环境准备✅ Docker Compose(多库 & 读…...

jenkins 启动报错
java.lang.UnsatisfiedLinkError: /opt/application/jdk-17.0.11/lib/libfontmanager.so: libfreetype.so.6: cannot open shared object file: No such file or directory。 解决方案: yum install freetype-devel 安装完成之后重启jenkins。...

C++ 套接字函数详细介绍
目录 头文件1. 套接字创建与配置2. 绑定地址与端口3. 连接建立4. 数据传输5. 套接字选项6. 地址转换7. 套接字关闭8. 其他实用函数 C 套接字函数详细介绍 套接字(Socket)是网络通信的基本端点,C中通常使用BSD套接字API进行网络编程。以下是主要的套接字相关函数及其…...

【合新通信】无人机天线拉远RFOF(射频光纤传输)解决方案
无人机天线拉远RFOF方案通过光纤替代传统射频电缆,实现无人机与地面控制站之间的高保真、低损耗信号传输,尤其适用于高频段(如毫米波)、远距离或复杂电磁环境下的无人机作业场景。 核心应用场景 军事侦察与电子战 隐蔽部署&…...

程序设计语言----软考中级软件设计师(自用学习笔记)
目录 1、解释器和编译器 2、程序的三种控制结构 3、程序中的数据必须具有类型 4、编译、解释程序翻译阶段 5、符号表 6、编译过程 7、上下文无关文法 8、前、中、后缀表达式 9、前、后缀表达式计算 10、语法树中、后序遍历 11、脚本语言和动态语言 12、语法分析方法…...

火山RTC 7 获得远端裸数据
一、获得远端裸数据 1、获得h264数据 1)、远端编码后视频数据监测器 /*** locale zh* type callback* region 视频管理* brief 远端编码后视频数据监测器<br>* 注意:回调函数是在 SDK 内部线程(非 UI 线程)同步抛出来的&a…...

通过SMTP协议实现Linux邮件发送配置指南
一、环境准备与基础配置 1. SMTP服务开通(以qq邮箱为例) 登录qq邮箱网页端,进入「设置」-「POP3/SMTP/IMAP」 开启「SMTP服务」并获取16位授权码(替代邮箱密码使用) 记录关键参数: SMTP服务器地址&#…...

若依框架页面
1.页面地址 若依管理系统 2.账号和密码 管理员 账号admin 密码admin123 运维 账号yuwei 密码123456 自己搭建的地址方便大家学习,不要攻击哦,谢谢啊...

44、私有程序集与共享程序集有什么区别?
私有程序集(Private Assembly)与共享程序集(Shared Assembly)是.NET框架中程序集部署的两种不同方式,它们在部署位置、版本控制、访问权限等方面存在显著差异,以下是对二者的详细比较: 1. 部署…...

【Java面试题】——this 和 super 的区别
🎁个人主页:User_芊芊君子 🎉欢迎大家点赞👍评论📝收藏⭐文章 🔍系列专栏:【Java】内容概括 【前言】 在Java的世界里,this和 super是两个非常重要且容易混淆的关键字。无论是在日常…...
Linux下QFileDialog没反应))
记录 QT 在liunx 下 QFileDialog 类调用问题 ()Linux下QFileDialog没反应)
1. 2025.05.14 踩坑记录 因为QT 在 liunx 文件系统不同导致的 Windows : QString filePath QFileDialog::getOpenFileName(nullptr, "选择文件", ".", "文本文件 (*.txt);所有文件 (*.*)"); 没问题 liunx 下 打不开ÿ…...

CentOS 7 内核升级指南:解决兼容性问题并提升性能
点击上方“程序猿技术大咖”,关注并选择“设为星标” 回复“加群”获取入群讨论资格! CentOS 7 默认搭载的 3.10.x 版本内核虽然稳定,但随着硬件和软件技术的快速发展,可能面临以下问题: 硬件兼容性不足:新…...

【前端】:单 HTML 去除 Word 批注
在现代办公中,.docx 文件常用于文档编辑,但其中的批注(注释)有时需要在分享或归档前被去除。本文将从原理出发,深入剖析如何在纯前端环境下实现对 .docx 文件注释的移除,并提供完整的实现源码。最后&#x…...
