广度和深度优先搜索(BFS和DFS)
1. 广度和深度优先搜索(BFS和DFS)
1.1. Python实现BFS和DFS
from collections import dequeclass Graph:"""无向图类,支持添加边,并实现了 BFS(广度优先搜索)和 DFS(深度优先搜索)用于查找从一个顶点到另一个顶点的路径。"""def __init__(self, v):self.v = v # 顶点数self.adj = [[] for _ in range(v)] # 邻接表,初始化为空列表self.found = False # DFS 中用于标记是否已经找到目标节点def add_edge(self, s, t):self.adj[s].append(t)self.adj[t].append(s) # 因为是无向图,所以两个方向都要添加def bfs(self, s, t):if s == t:print(s)returnvisited = [False] * self.v # 标记每个节点是否访问过visited[s] = Truequeue = deque()queue.append(s)prev = [-1] * self.v # 用于记录路径,prev[i] 表示访问 i 节点的前一个节点while queue:w = queue.popleft()for q in self.adj[w]:if not visited[q]:prev[q] = wif q == t:self._print_path(prev, s, t)returnvisited[q] = Truequeue.append(q)print("No path found.")def dfs(self, s, t):self.found = Falsevisited = [False] * self.vprev = [-1] * self.vself._recur_dfs(s, t, visited, prev)if self.found:self._print_path(prev, s, t)else:print("No path found.")def _recur_dfs(self, w, t, visited, prev): # DFS的递归辅助函数if self.found:returnvisited[w] = Trueif w == t:self.found = Truereturnfor q in self.adj[w]:if not visited[q]:prev[q] = wself._recur_dfs(q, t, visited, prev)def _print_path(self, prev, s, t): # 打印从 s 到 t 的路径,基于 prev 反向回溯。if prev[t] != -1 and t != s:self._print_path(prev, s, prev[t])print(t, end=' ')
1.2. 广度优先搜索(BFS)
BFS的定义:
广度优先搜索(Breadth-First-Search),简称为 BFS。它其实就是一种“地毯式”层层推进的搜索策略,即先查找离起始顶点最近的,然后是次近的,依次往外搜索。
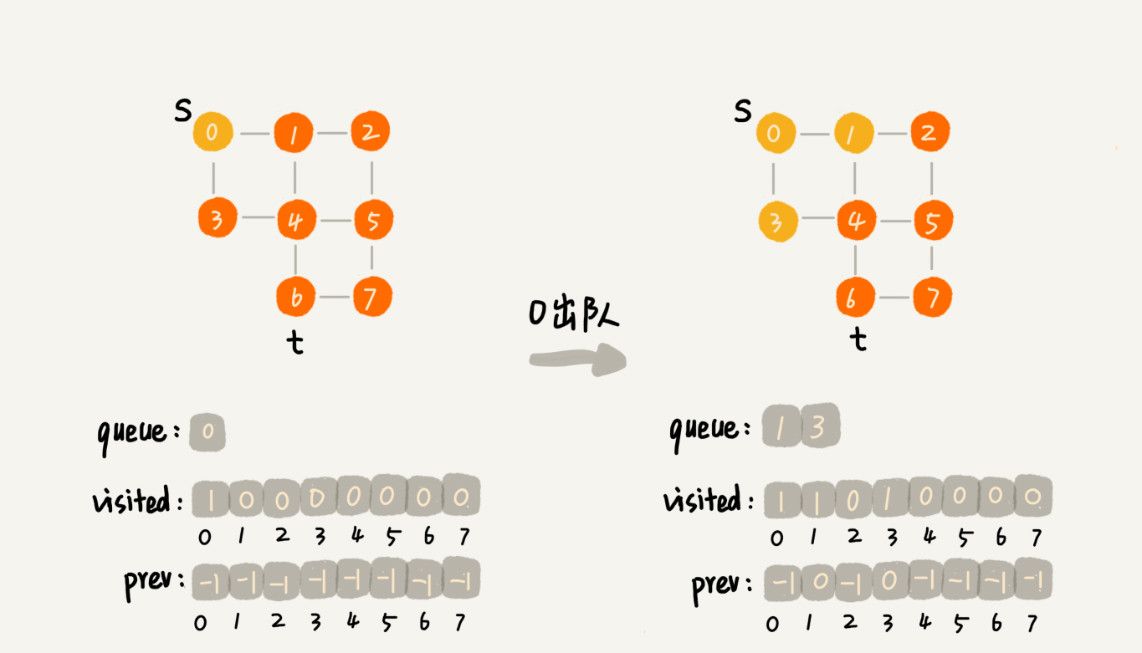
核心辅助变量:
- visited是用来记录已经被访问的顶点,用来避免顶点被重复访问。如果顶点 q 被访问,那相应的 visited[q] 会被设置为 true。
- queue是一个队列,用来存储已经被访问、但相连的顶点还没有被访问的顶点。因为广度优先搜索是逐层访问的,也就是说,我们只有把第 k 层的顶点都访问完成之后,才能访问第 k+1 层的顶点。当我们访问到第 k 层的顶点的时候,我们需要把第 k 层的顶点记录下来,稍后才能通过第 k 层的顶点来找第 k+1 层的顶点。所以,我们用这个队列来实现记录的功能。
- prev用来记录搜索路径。当我们从顶点 s 开始,广度优先搜索到顶点 t 后,prev 数组中存储的就是搜索的路径。不过,这个路径是反向存储的。prev[w] 存储的是,顶点 w 是从哪个前驱顶点遍历过来的。比如,我们通过顶点 2 的邻接表访问到顶点 3,那 prev[3] 就等于 2。为了正向打印出路径,我们需要递归地来打印,你可以看下 print() 函数的实现方式。
时间和空间复杂度:
V 表示顶点的个数,E 表示边的个数。
- 时间复杂度:O(V + E) ,简写为 O(E)
对于一个连通图来说,也就是说一个图中的所有顶点都是连通的,E 肯定要大于等于 V-1,所以,广度优先搜索的时间复杂度也可以简写为 O(E)。
- 空间复杂度:O(V)
1.3. 深度优先搜索(DFS)
DFS的概念:
- 类似“走迷宫”;
- 一路走到底,走不通就回退,再尝试其他路径;
- 非最短路径,但能遍历所有可能路径。
特点:
- 用递归方式实现,体现回溯思想;
- 辅助变量同 BFS,额外用 found 控制递归终止。
时间和空间复杂度:
- 时间复杂度: O(E)
- 空间复杂度:O(V)
BFS vs DFS:
| 特性 | BFS | DFS |
| 搜索策略 | 按层次,逐层推进 | 一路深入,回退再尝试 |
| 是否找最短路径 | ✅ 是 | ❌ 不一定 |
| 实现方式 | 通常用队列实现 | 通常用递归或栈实现 |
| 时间复杂度 | O(V + E) | O(V + E) |
| 空间复杂度 | O(V) | O(V) |
| 推荐使用场景 | 路径最短查找、三度好友推荐等 | 遍历所有可能路径、连通性检 |
相关文章:

广度和深度优先搜索(BFS和DFS)
1. 广度和深度优先搜索(BFS和DFS) 1.1. Python实现BFS和DFS from collections import dequeclass Graph:"""无向图类,支持添加边,并实现了 BFS(广度优先搜索)和 DFS(深度优先搜…...

【计算机视觉】OpenCV实战项目:Text-Extraction-Table-Image:基于OpenCV与OCR的表格图像文本提取系统深度解析
Text-Extraction-Table-Image:基于OpenCV与OCR的表格图像文本提取系统深度解析 1. 项目概述2. 技术原理与算法设计2.1 图像预处理流水线2.2 表格结构检测算法2.3 OCR优化策略 3. 实战部署指南3.1 环境配置3.2 核心代码解析3.3 执行流程示例 4. 常见问题与解决方案4.…...

嵌入式Linux Qt开发:1、搭建基于ubuntu18.04的Qt开发环境及测试(解决Qt creator输入法问题)
一、前言 基本在我职业生涯开始时就已经在使用Qt进行一些上位机开发了,后续也有一些嵌入式设备用Qt开发,但是一直没有完整和系列的总结,包括C也是,这里慢慢补上一些总结,防止很多经验总结和学习过程又遗忘了ÿ…...
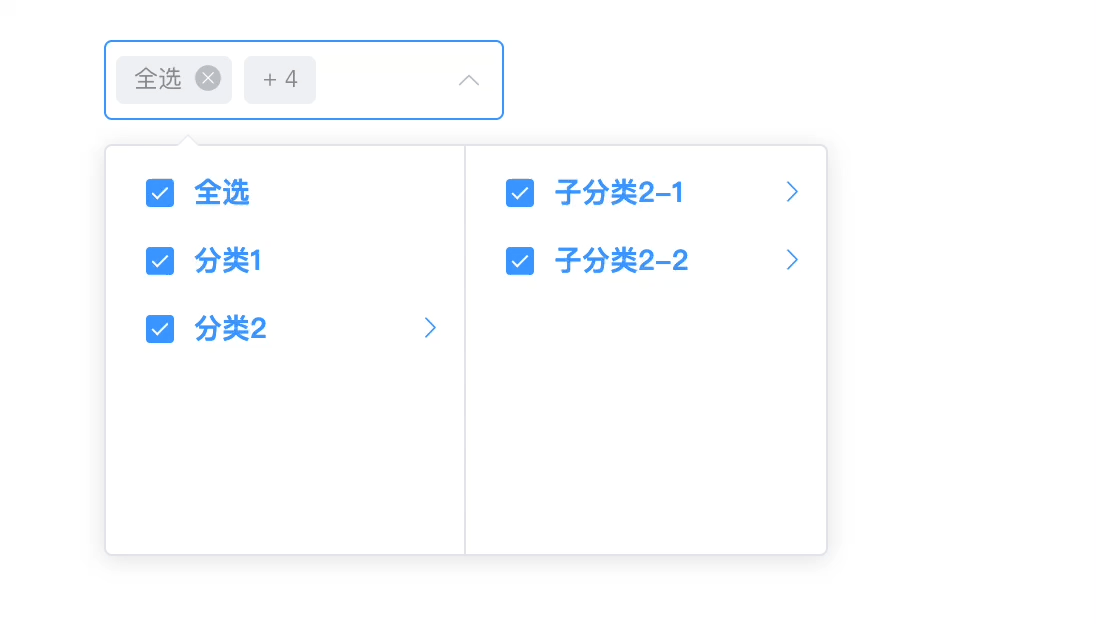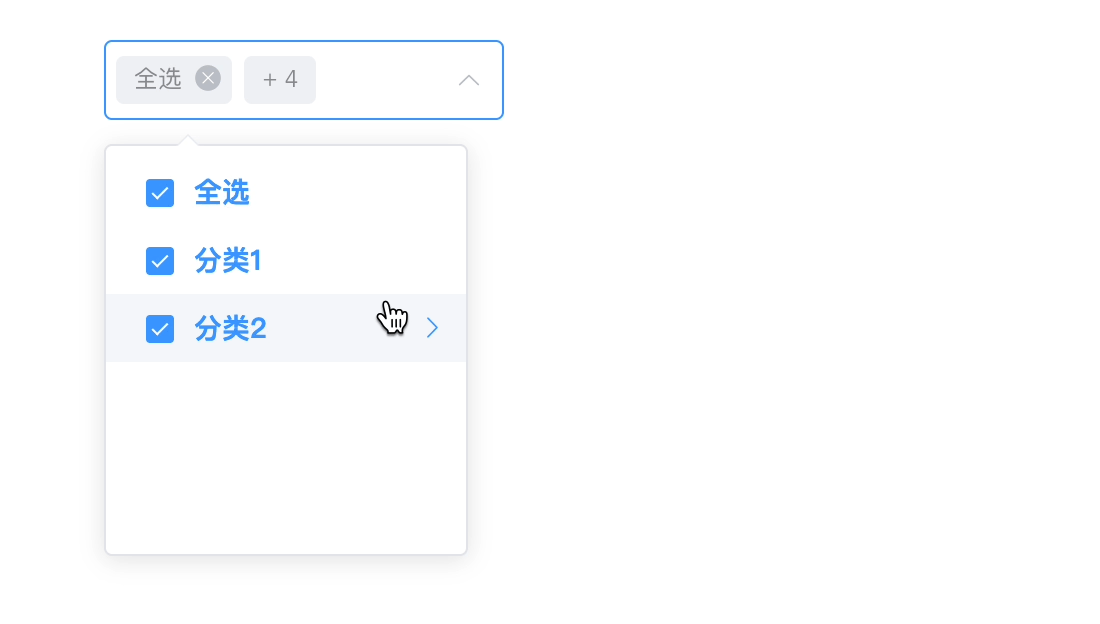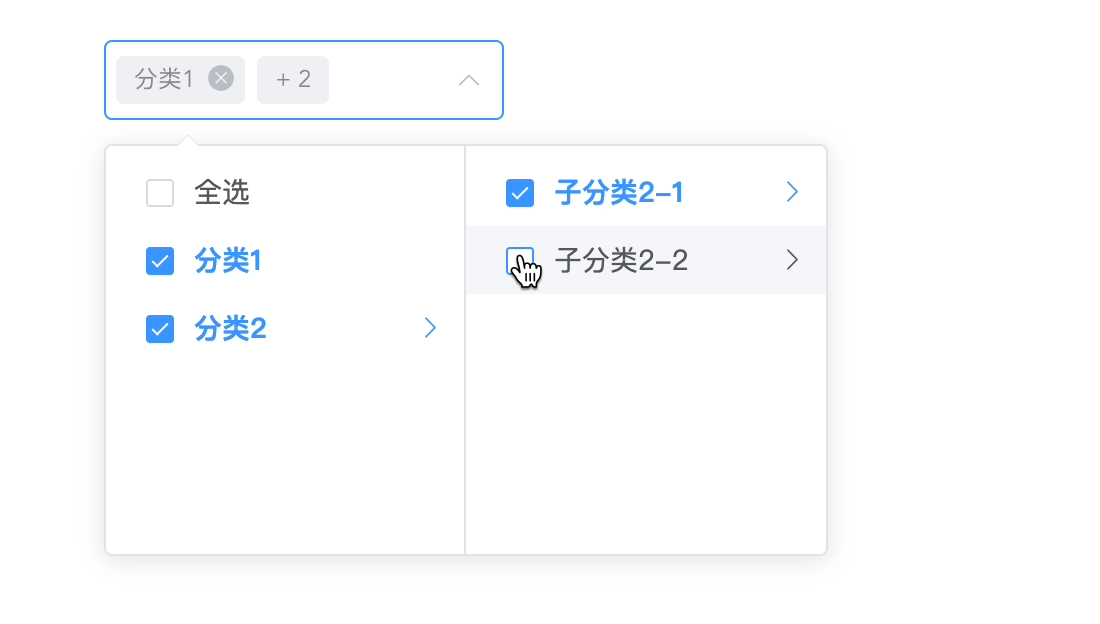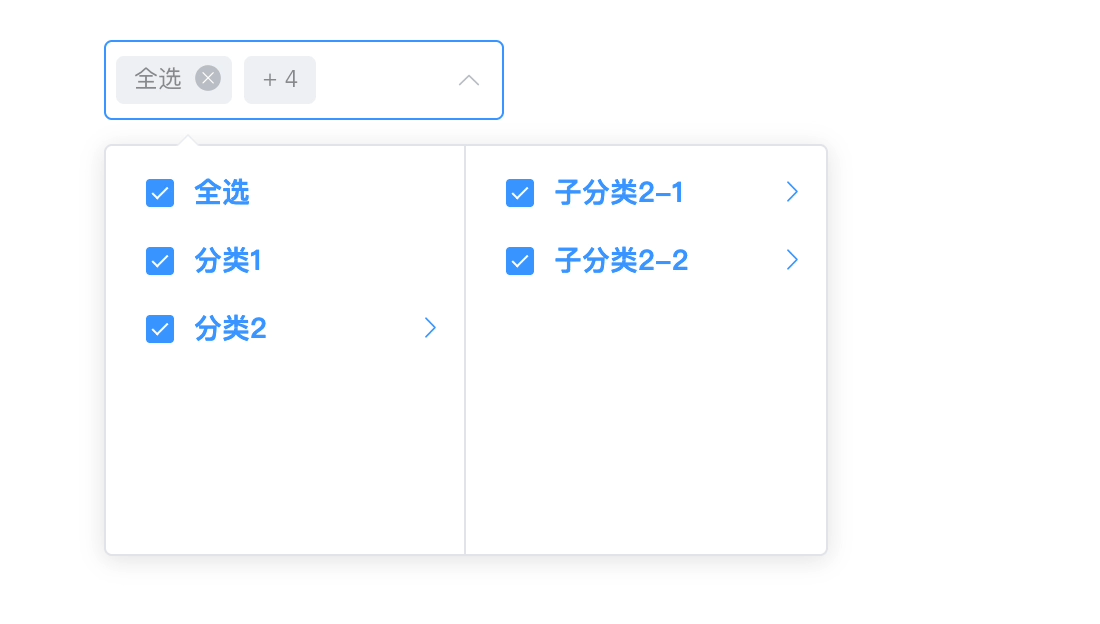
element-ui的el-cascader增加全选按钮实现(附源码)
最近遇到了在级联选择器上添加全选框的需求 ,但是项目使用的是Vue2 Element UI的架构,而我们都知道Element UI提供的级联选择器el-cascader是不支持全选框的,而我又没有在网上找到适合我项目的实现,索性自己实现一个组件…...

Scratch游戏 | 企鹅大乱斗
有没有过无聊到抓狂的时刻?试试这款 企鹅大乱斗 吧!超简单的玩法,让你瞬间告别无聊! 🎮 玩法超简单 等待屏幕出现 ”Go!” 疯狂点击,疯狂拍打企鹅! 💥 游戏特色 解压神器&#x…...

游戏行业DDoS攻击类型及防御分析
游戏行业作为DDoS攻击的高发领域,攻击类型复杂多样,结合多个来源的信息,以下是其主要攻击类型及特征分析: 1. 传统流量型DDoS攻击 UDP洪水攻击:通过大量UDP报文淹没服务器端口,消耗带宽资源,导…...

Uniapp中小程序调用腾讯地图(获取定位地址)
1、先配置权限: 这是上图的代码: "permission": { "scope.userLocation": { "desc": "你的位置信息将用于小程序位置接口的效果展示" } } 第二步:写代码: //下面是uniapp的模版代码 主…...
2025全网首发:ComfyUI整合GPT-Image-1完全指南 - 8步实现AI图像创作革命
ComfyUI整合GPT-Image-1完全指南:8步实现AI图像创作革命【2025最新】 OpenAI最新发布的GPT-Image-1模型(也就是ChatGPT-4o背后的图像生成技术)已经通过API开放使用,而令人惊喜的是,ComfyUI已经第一时间提供了完整支持&…...

利用SAP aATP产品分段策略应对订单关税挑战
本文探讨了如何通过在SAP S/4HANA系统中结合**产品分段(Product Segmentation)与高级可承诺性(aATP)**功能,帮助企业在全球化贸易中更有效地处理关税问题,并提升订单承诺的精准性。 产品分段与原产国&…...

工业4.0神经嫁接术:ethernet ip转profinet协议通信步骤图解
在现代工业自动化领域,不同品牌的设备和协议之间的兼容性问题一直是个挑战。我们的包装线项目就遇到了这样的难题:需要将Rockwell Allen-Bradley的EtherNet/IP伺服系统与西门子PLC的PROFINET主站进行无缝对接。为了解决这一问题,我们采用了et…...

深入理解反序列化攻击:原理、示例与利用工具实战
反序列化漏洞是现代 Web 安全中的一个高危攻击类型,常常导致远程代码执行(RCE)、文件读写、身份伪造等严重后果。本文将从基础原理讲起,结合实际代码和工具(PHPGGC、ysoserial)演示反序列化攻击的完整过程。…...

Qt原型模式实现与应用
在Qt中实现原型模式(Prototype Pattern)可以通过以下步骤完成。该模式的核心是通过克隆现有对象来创建新对象,而非通过传统的构造函数。以下是详细说明和示例: 1. 原型模式的核心概念 目的:避免重复初始化对象的高成本…...
:LeetCode 41. 缺失的第一个正数(First Missing Positive)详解)
Java详解LeetCode 热题 100(17):LeetCode 41. 缺失的第一个正数(First Missing Positive)详解
文章目录 1. 题目描述2. 理解题目3. 解法一:排序法(不满足题目要求)3.1 思路3.2 Java代码实现3.3 代码详解3.4 复杂度分析3.5 不足之处 4. 解法二:哈希表法4.1 思路4.2 Java代码实现4.3 代码详解4.4 复杂度分析4.5 不足之处 5. 解…...
)
[Java实战]Spring Boot + Netty 实现 TCP 长连接客户端及 RESTful 请求转发(二十六)
[Java实战]Spring Boot Netty 实现 TCP 长连接客户端及 RESTful 请求转发(二十六) 在现代微服务架构中,经常需要在不同服务之间进行高效、可靠的通信。本文将介绍如何使用 Spring Boot 结合 Netty 实现一个 TCP 长连接客户端,并…...

【Linux】动静态库的使用
📝前言: 这篇文章我们来讲讲Linux——动静态库的使用 🎬个人简介:努力学习ing 📋个人专栏:Linux 🎀CSDN主页 愚润求学 🌄其他专栏:C学习笔记,C语言入门基础&…...
Java基础(网络编程)
一、概述 目的:网络通信: 1、设备和设备 2、进程和进程 1)不同设备之间 2)本地设备之间 需要解决的问题: 如何准确地发送到对方的主机 - IP地址 - 唯一的定位网络中的一台主机 如何准确的发送到对方主机的进程 -…...

计量——异方差的检验及其修正
目录 1.异方差的检验 1 BP检验 2white检验 2.异方差的修正 1.异方差的检验 1 BP检验 选择检验方法:BP BP检验的实际步骤(非机器): 1.y对所有x进行回归,得到残差u。计算残差的平方u^2 2.u^2对所有x进行回归&#…...

学习C++的好书:C++编程之禅
历时四个月,把这本书看了一遍,受益匪浅,推荐给大家,系统的学习一遍C。...

OpenCV进阶操作:人脸检测、微笑检测
文章目录 前言一、OpenCV如何实现人脸检测1、haar特征2、级联分类器3、级联分类器的使用 二、人脸检测、微笑检测 案例实现1、预处理2、加载分类器3、标注人脸4、运行结果:4、微笑检测 总结 前言 要实现人脸识别首先要判断当前图像中是否出现了人脸,这就…...

车载诊断进阶篇 --- 车载诊断概念
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 钝感力的“钝”,不是木讷、迟钝,而是直面困境的韧劲和耐力,是面对外界噪音的通透淡然。 生活中有两种人,一种人格外在意别人的眼光;另一种人无论…...

制作一款打飞机游戏49:敌人抖动
蛇形敌人 如果你玩过一些射击游戏(shmups),尤其是老式的射击游戏,你可能会遇到一种敌人,它们像蛇一样移动。我想在我们的游戏中实现这种效果。这种动态的感觉非常棒,我们完全有能力通过动画来实现它。 方…...

elementplus el-tree 二次封装支持配置删除后展示展开或折叠编辑复选框懒加载功能
本文介绍了基于 ElementPlus 的 el-tree 组件进行二次封装的 TreeView 组件,使用 Vue3 和 JavaScript 实现。TreeView 组件通过 props 接收树形数据、配置项等,支持懒加载、节点展开/收起、节点点击、删除、编辑等操作。组件内部通过 ref 管理树实例&…...

Pycharm IDEA加载大文件时报错:The file size exceeds configured limit
解决方案:配置一下idea.properties文件 文件里面写入代码: idea.max.intellisense.filesize50000重启IDEA即可;...

free void* 指令
https://stackoverflow.com/questions/2182103/is-it-ok-to-free-void free(ptr) 仅释放指针指向的内存,不会修改指针变量本身的值。调用后,ptr 仍然指向原来的地址(称为 "悬空指针"),但该地址对应的内存已…...

PDA手持终端应用有哪些?
随着技术进步不断拓展,PDA手持终端其便携性与多功能特性使其成为多行业数字化转型的核心工具。主要包括物流与仓储管理、零售行业、医疗行业以及制造业等。 1.物流与仓储管理 在物流与仓储管理中,PDA手持终端主要用于物品的实时跟踪、库存管理和拣货作业…...

Python模块化编程
Python模块化编程 记得我刚学Python那会儿,特别喜欢把所有代码都写在一个文件里。直到有一天,我的项目膨胀到了2000多行代码,每次修改都要翻半天…这才痛定思痛,开始研究模块化编程。今天就跟大家聊聊这个让代码变得优雅的魔法。…...

Linux性能分析工具perf
perf 工具详解 perf(Performance Counters for Linux)是 Linux 系统上的一个强大的性能分析工具,用于监控和分析系统及应用程序的性能。它基于 Linux 内核的 Performance Event Subsystem(perf_events),能…...

Android开发-使用内容组件获取通讯信息
在Android开发中,访问和处理用户的通讯信息(如联系人、通话记录等)是一项常见的需求。通过使用Android的内容提供者(ContentProvider),开发者可以方便地查询这些数据,并将其集成到自己的应用中。…...

文件目录与检索综合练习题
文章目录 前言一、基础部分二、参数应用三、参数进阶四、组合应用五、归档压缩六、统计与分析总结 前言 这部分练习题帮助大家更好的掌握命令 一、基础部分 1.用grep在error.log中查找所有含"Timeout"的行 2.使用find在/var/log下搜索7天内修改过的.log文件 3.对da…...
Python+Selenium爬虫:豆瓣登录反反爬策略解析
1. 引言 在当今互联网时代,数据抓取(爬虫)技术广泛应用于数据分析、市场调研、自动化测试等领域。然而,许多网站采用动态加载技术(如Ajax、React、Vue.js等框架)来渲染页面,传统的**<font s…...
