合并两个有序数组的高效算法详解
合并两个有序数组的高效算法详解
- **合并两个有序数组的高效算法详解**
- **1. 问题描述**
- **2. 常见解法分析**
- **方法 1:合并后排序(暴力法)**
- **方法 2:双指针法(额外空间)**
- **3. 最优解法:双指针从后向前合并**
- **核心思路**
- **代码实现**
- **复杂度分析**
- **示例演示**
- **4. 关键点总结**
- **5. 扩展思考**
- **6. 总结**
合并两个有序数组的高效算法详解
1. 问题描述
给定两个按 非递减顺序 排列的整数数组 nums1 和 nums2,以及两个整数 m 和 n,分别表示 nums1 和 nums2 中的元素数目。
要求:
- 将
nums2合并到nums1中,使合并后的数组仍然保持 非递减顺序。 nums1的初始长度为m + n,其中后n个元素为0,表示应被nums2填充的位置。
示例:
输入:
nums1 = [1, 2, 3, 0, 0, 0], m = 3
nums2 = [2, 5, 6], n = 3输出:
[1, 2, 2, 3, 5, 6]
2. 常见解法分析
方法 1:合并后排序(暴力法)
思路:
- 将
nums2的所有元素直接放入nums1的末尾。 - 对整个
nums1进行排序。
代码:
public void merge(int[] nums1, int m, int[] nums2, int n) {for (int i = 0; i < n; i++) {nums1[m + i] = nums2[i];}Arrays.sort(nums1);
}
复杂度分析:
- 时间复杂度:
O((m+n) log(m+n))(排序的时间复杂度) - 空间复杂度:
O(1)(未使用额外空间)
缺点:
- 没有利用
nums1和nums2已经有序 的特性,导致时间复杂度较高。
方法 2:双指针法(额外空间)
思路:
- 创建一个临时数组
temp,用两个指针分别遍历nums1和nums2,按顺序选择较小的元素放入temp。 - 最后将
temp复制回nums1。
代码:
public void merge(int[] nums1, int m, int[] nums2, int n) {int[] temp = new int[m + n];int i = 0, j = 0, k = 0;while (i < m && j < n) {if (nums1[i] <= nums2[j]) {temp[k++] = nums1[i++];} else {temp[k++] = nums2[j++];}}while (i < m) temp[k++] = nums1[i++];while (j < n) temp[k++] = nums2[j++];System.arraycopy(temp, 0, nums1, 0, m + n);
}
复杂度分析:
- 时间复杂度:
O(m + n) - 空间复杂度:
O(m + n)(需要额外数组)
缺点:
- 需要额外的
O(m+n)空间,不符合题目对空间复杂度的优化要求。
3. 最优解法:双指针从后向前合并
核心思路
由于 nums1 的后面有足够的空间(填充 0),我们可以 从后向前 合并,避免覆盖 nums1 前面的数据。
步骤:
- 初始化三个指针:
i = m - 1(nums1有效部分的末尾)j = n - 1(nums2的末尾)k = m + n - 1(nums1最终合并后的末尾)
- 比较
nums1[i]和nums2[j],将较大的数放入nums1[k],并移动指针。 - 如果
nums2还有剩余元素,直接复制到nums1前面。
代码实现
public void merge(int[] nums1, int m, int[] nums2, int n) {int i = m - 1, j = n - 1, k = m + n - 1;while (j >= 0) { // 只需要处理 nums2 剩余元素if (i >= 0 && nums1[i] > nums2[j]) {nums1[k--] = nums1[i--];} else {nums1[k--] = nums2[j--];}}
}
复杂度分析
- 时间复杂度:
O(m + n)(只需遍历nums1和nums2各一次) - 空间复杂度:
O(1)(原地修改,无额外空间)
示例演示
输入:
nums1 = [1, 2, 3, 0, 0, 0], m = 3
nums2 = [2, 5, 6], n = 3
执行过程:
| 步骤 | i | j | k | nums1[i] | nums2[j] | 操作 | nums1 结果 |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 2 | 5 | 3 | 6 | nums1[5] = 6 | [1,2,3,0,0,6] |
| 2 | 2 | 1 | 4 | 3 | 5 | nums1[4] = 5 | [1,2,3,0,5,6] |
| 3 | 2 | 0 | 3 | 3 | 2 | nums1[3] = 3 | [1,2,3,3,5,6] |
| 4 | 1 | 0 | 2 | 2 | 2 | nums1[2] = 2 | [1,2,2,3,5,6] |
| 5 | 1 | -1 | 1 | - | - | j < 0 退出循环 | 合并完成 |
最终结果:
[1, 2, 2, 3, 5, 6]
4. 关键点总结
-
为什么从后向前合并?
nums1后面有足够的空间,不会覆盖未处理的元素。- 如果从前向后合并,需要额外空间存储被覆盖的数据。
-
为什么
while (j >= 0)就够了?- 只要
nums2合并完成,nums1剩余部分已经在正确位置,无需处理。
- 只要
-
边界情况处理:
nums1为空 → 直接复制nums2。nums2为空 →nums1保持不变。
5. 扩展思考
-
如果
nums1和nums2不是有序的,如何优化?
→ 先排序再合并,但时间复杂度会上升至O((m+n) log(m+n))。 -
如果要求返回新数组而不是修改
nums1?
→ 可以用 方法 2(双指针 + 额外空间)。
6. 总结
| 方法 | 时间复杂度 | 空间复杂度 | 适用场景 |
|---|---|---|---|
| 合并后排序 | O((m+n) log(m+n)) | O(1) | 简单但效率低 |
| 双指针(额外空间) | O(m+n) | O(m+n) | 需要新数组时 |
| 双指针(原地合并) | O(m+n) | O(1) | 最优解 |
推荐使用双指针从后向前合并,既高效又节省空间! 🚀
相关文章:

合并两个有序数组的高效算法详解
合并两个有序数组的高效算法详解 **合并两个有序数组的高效算法详解****1. 问题描述****2. 常见解法分析****方法 1:合并后排序(暴力法)****方法 2:双指针法(额外空间)** **3. 最优解法:双指针从…...
)
虚拟Python 环境构建器virtualenv安装(macOS版)
前提 之前我们使用pyenv安装好了Python 3.13.3,并且,全局都使用这个版本的python。现在我们来安装virtualenv。 pipx安装 brew install pipx pipx ensurepath sudo pipx ensurepath --global # optional to allow pipx actions with --global argumen…...

解决ubuntu20中tracker占用过多cpu,引起的风扇狂转
track是linux中的文件索引工具,ubuntu18之前是默认不安装的,所以在升级到20后会默认安装,它是和桌面程序gnome绑定的,甚至还有很多依赖项,导致无法删除,一旦删除很多依赖项都不能运行,禁用也很难…...

在线文档管理系统 spring boot➕vue|源码+数据库+部署教程
📌 一、项目简介 本系统采用Spring Boot Vue ElementUI技术栈,支持管理员和员工两类角色,涵盖文档上传、分类管理、公告发布、员工资料维护、部门岗位管理等核心功能。 系统目标是打造一个简洁高效的内部文档管理平台,便于员工…...
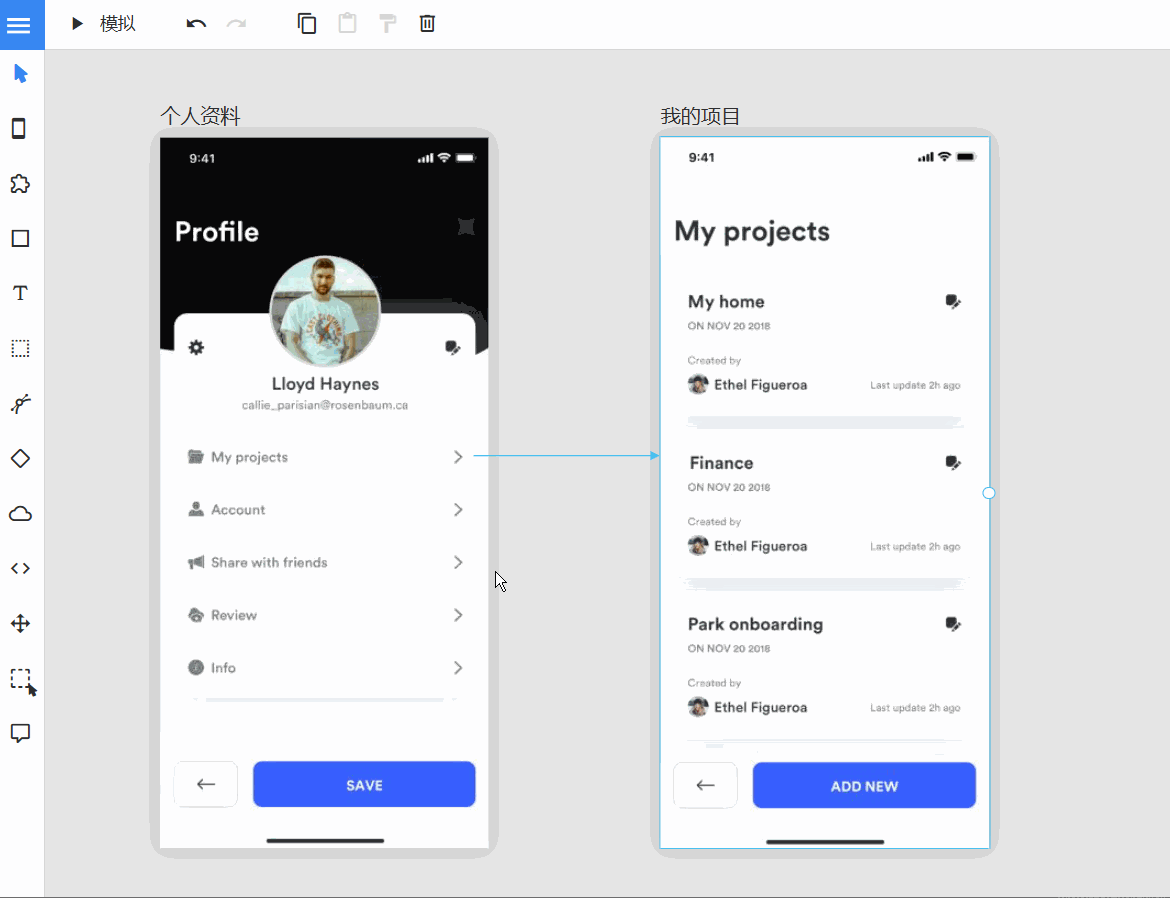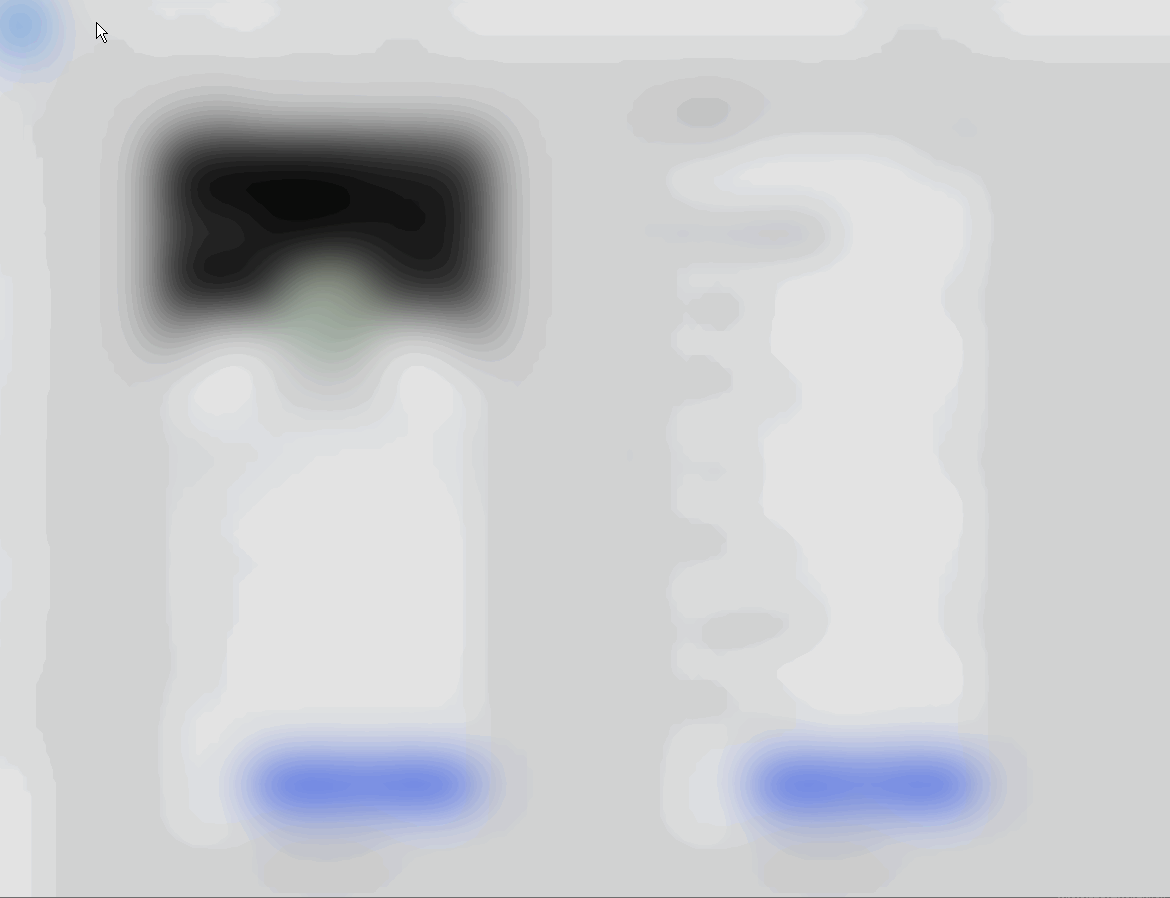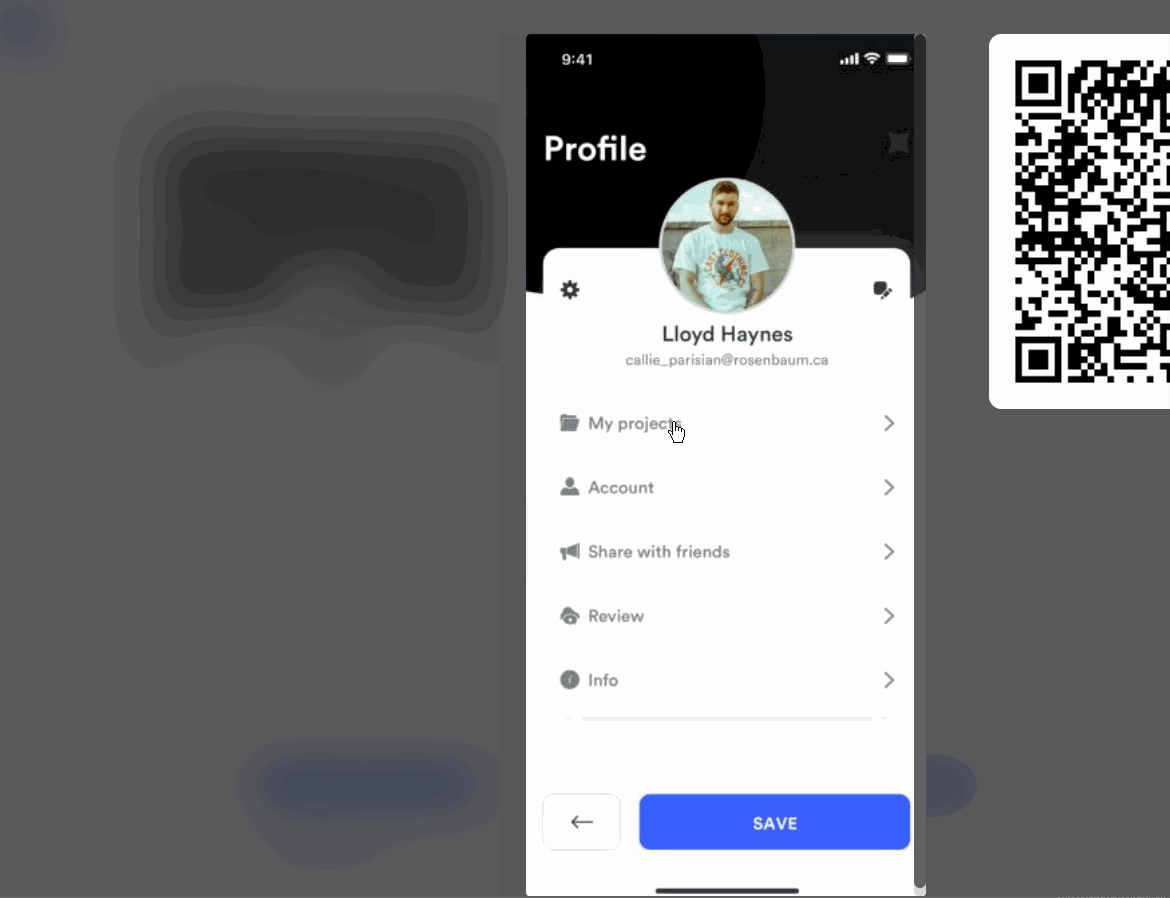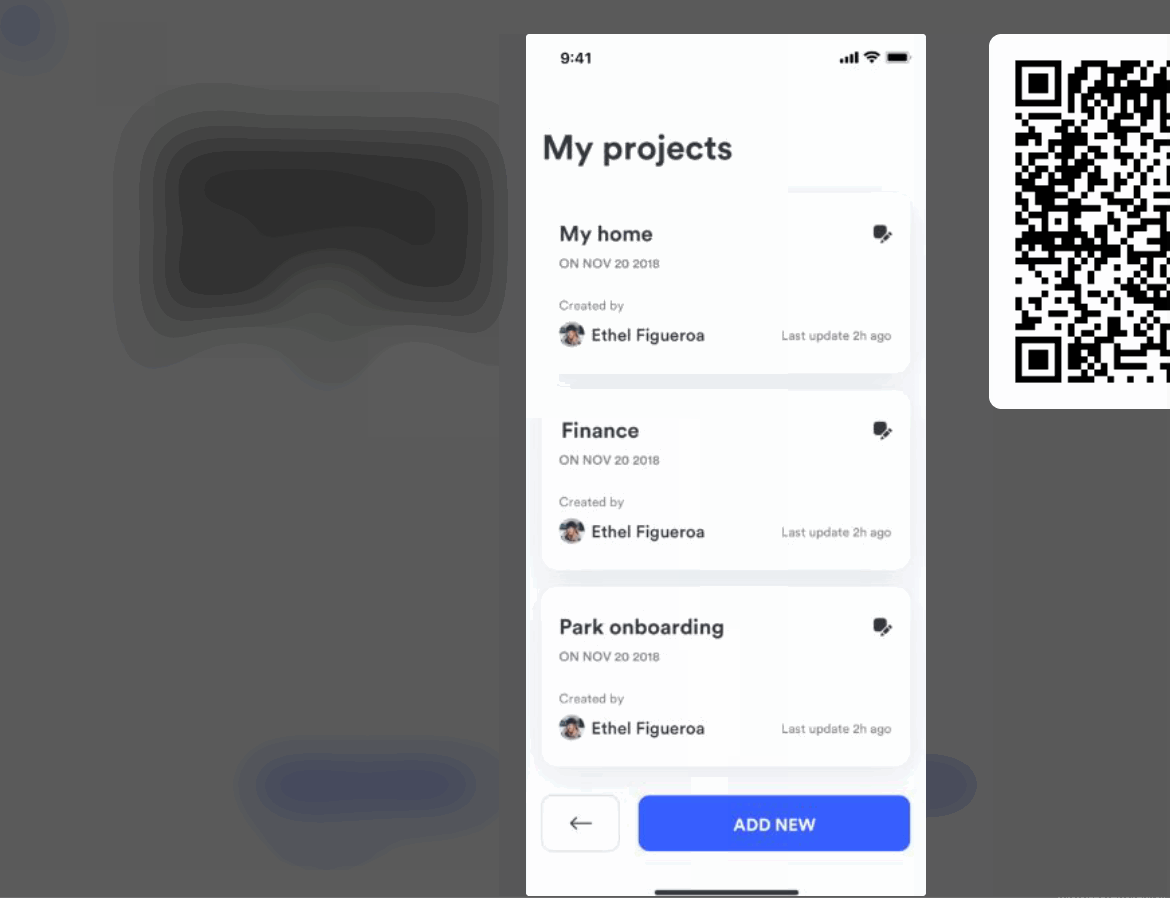
在UI 原型设计中,交互规则有哪些核心要素?
在UI 原型设计中,交互规则主要有三个核心要素,分别为重要性、原则与实践,具体表现在: 一、交互规则在 UI 原型设计中的重要性 明确交互逻辑:设计阶段制定交互规则,清晰定义界面元素操作响应。 如社交应用…...

CSS图片垂直居中问题解决方案
在 CSS 中,使用 vertical-align: middle 导致图片略微向下偏移的现象,本质上是由于 行内元素的基线对齐规则 和 父容器上下文环境 共同作用的结果。以下是具体原因和解决方案: 原因详解 1. vertical-align: middle 的真实含义 该属性 不会让…...

STC8H系列单片机STC8H_H头文件功能注释
#ifndef __STC8H_H__ // 条件编译:如果未定义__STC8H_H__宏 #define __STC8H_H__ // 则定义该宏,防止头文件被重复包含 / //包含本头文件后,不用另外再包含"REG51.H" // 提示:本头文件已包含基本寄存器定义 sfr P0 = …...

Python类的力量:第五篇:魔法方法与协议——让类拥有Python的“超能力”
文章目录 前言:从“普通对象”到“Python原生公民”的进化之路 一、魔法方法:赋予对象“超能力”的基因1. 构造与析构:对象生命周期的“魔法开关”2. 字符串表示:对象的“自我介绍”3. 运算符重载:让对象支持“数学魔法…...

OpenResty Manager 介绍与部署(Docker部署)
概述 OpenResty-Manager 是一个基于 OpenResty 构建的开源 Web 管理平台。OpenResty 是一个高性能的 Web 平台,集成了 Nginx 和 LuaJIT,支持强大的脚本功能。OpenResty-Manager 由 Safe3 开发,提供了一个用户友好的界面,用于管理…...

深入解析HTTP协议演进:从1.0到3.0的全面对比
HTTP协议作为互联网的基础协议,经历了多个版本的迭代演进。本文将详细解析HTTP 1.0、HTTP 1.1、HTTP/2和HTTP/3的核心特性与区别,帮助开发者深入理解网络协议的发展脉络。 一、HTTP 1.0:互联网的奠基者 核心特点: 短连接模式&am…...

快速搭建一个electron-vite项目
1. 初始化项目 在命令行中运行以下命令 npm create quick-start/electronlatest也可以通过附加命令行选项直接指定项目名称和你想要使用的模版。例如,要构建一个 Electron Vue 项目,运行: # npm 7,需要添加额外的 --: npm cre…...

【Android】Android 实现一个依赖注入的注解
Android 实现一个依赖注入的注解 🎯 目标功能 自定义注解 Inject创建一个 Injector 类,用来扫描并注入对象支持 Activity 或其他类中的字段注入 🧩 步骤一:定义注解 import java.lang.annotation.ElementType; import java.lan…...

unity terrain 在生成草,树,石头等地形障碍的时候,无法触发碰撞导致人物穿过模型
1.terrain地形的草,石头之类要选择模型预制体 2.在人物身上挂碰撞器和刚体,或者单挂一个character controller组件也行 3.在预制体上挂碰撞盒就好了,挂载meshcollider会导致碰撞无效...

使用gitbook 工具编写接口文档或博客
步骤一:在项目目录中初始化一个 GitBook 项目 mkdir mybook && cd mybook git init npm init -y步骤二:添加书籍结构(如 book.json, README.md) echo "# 我的书" > README.md echo "{}" > bo…...

75.xilinx复数乘法器IP核调试
(83*j)*(57j) 935j 正确的是 1971j 分析出现的原因:(abj)* (cdj) (ac-bd)j(adbc) 其中a,b,c,d都是16bit的有符号数,乘积的结果为保证不溢出需要32bit存储,最终的复数乘法结果是两个32b…...

软件工程之软件产品的环境
比较正规的做法是分下面的三个 1.开发环境(Development Environment): 用途:这是软件开发人员编写和测试代码的地方。在开发环境中,开发者可以自由地试验、调试代码,以及进行初步的功能实现和测试。 特点&…...

8.ADC
目录 ADC 模拟信号和数字信号的区别和区别 信号的区别 如何采集信号 常见的接口 数字接口 模拟接口 ADC 实际应用 ADC 转换器的定义 ADC 相关的名词 ADC 采集的原理 ADC 的参考电压 相关的计算 如何实现 ADC STM32 内的 ADC 转换器讲解 STM32 的 ADC 简介 AD…...

c/c++中程序内存区域的划分
c/c程序内存分配的几个区域: 1.栈区:在执行函数时,函数内局部变量的存储单元都可以在栈上创建,函数执行结束时这些存储单元自动被释放,栈内存分配运算内置于处理器的指令集中,效率很高但是分配的内存容量有…...

模糊综合评价模型建立
模糊综合评价模型建立 一、整体流程 二、代码实现(含大量注释) #程序文件ex14_4.py import numpy as npa np.loadtxt(data14_4.txt) # 使用定义匿名函数的形式来定义各个评价指标的隶属函数 f1 lambda x: x/8800 f2 lambda x: 1-x/8000 f3 lambda x: (x<5.5)(8-x)/(8-…...

【Linux】Linux安装mysql
该教程是使用的 CentOS 8.2 安装 mysql。 1.删除原有mysql rpm -qa|grep mariadb 如果存在在mariadb,卸载命令如下: #rpm -e --nodeps是强制卸载指令 后面是查出的依赖名称rpm -e --nodeps mariadb-libs-5.5.64-1.el7.x86_64全部卸载完输入以下指令&am…...

模仿学习笔记
模仿学习总共分两类: 行为克隆:BC,Dagger逆强化学习:又分为 2.1基于最大边际逆强化学习 (无法主要歧义问题):学徒学习 2.2 基于最大熵逆强化学习 (主要解决歧义问题):GAIL 学徒学习 基于最大熵…...

一文讲透 Vue3 + Three.js 材质属性之皮革篇【扫盲篇】
文章目录 前言一、Three.js材质系统基础1.1 为什么选择PBR材质?1.2 关键参数解析 二、不同类型皮革的材质配置2.1 牛皮材质实现2.2 羊皮材质实现2.3 仿皮材质实现 三、高级贴图技术3.1 贴图制作流程3.2 组合贴图实战 四、性能优化策略4.1 贴图压缩技术4.2 材质共享4…...

MUSE Pi Pro 使用TiTanTools烧录镜像
视频讲解: MUSE Pi Pro 使用TiTanTools烧录镜像 下载windows下的烧录工具 https://cloud.spacemit.com/prod-api/release/download/tools?tokentitantools_for_windows_X86_X64 下载镜像文件,zip后缀的即可 打开软件默认界面 按住FDL键,同时…...

奇变偶不变,符号看象限
三角函数诱导公式口诀详解:奇变偶不变,符号看象限 口诀解析 1. 口诀含义 奇变偶不变: 奇/偶:指角度加减的是π/2(90)的奇数倍还是偶数倍 奇数倍(如π/2, 3π/2)→ 函数名改变&…...

安卓A15系统实现修改锁屏界面默认壁纸功能
最近遇到一个A15系统项目,客户要求修改锁屏界面的默认壁纸,客户提供了一张壁纸图片,但是从A15系统的源代码查看时才知道谷歌已经去掉了相关的代码,已经不支持了,A13和A14系统好像是支持的,A15系统的Wallpap…...

IT系统的基础设施:流量治理、服务治理、资源治理,还有数据治理。
文章目录 引言I IT系统的基础设施流量治理、服务治理、资源治理,还有数据治理。开发语言的选择数据治理(监控系统):整体运维的数据其他II 基础知识的重要性第一,知道原理第二,当遇到一些比较难解的问题时,基础知识就会派上用场。例子III 大公司和小公司的权衡对比大公司…...

使用 TypeScript + dhtmlx-gantt 在 Next.js 中实现
1. 安装依赖(确保已安装) npm install dhtmlx-gantt2. 创建 pages/gantt.tsx use clientimport { useRef, useEffect } from react import { gantt } from dhtmlx-gantt import dhtmlx-gantt/codebase/dhtmlxgantt.cssinterface Task {id: number | st…...

解锁健康生活:现代养生实用方案
早上被闹钟惊醒后匆忙灌下咖啡,中午用外卖应付一餐,深夜刷着手机迟迟不肯入睡 —— 这样的生活模式,正在不知不觉侵蚀我们的健康。科学养生并非遥不可及的目标,只需从生活细节入手,就能逐步改善身体状态。 饮食管理…...

mongodb处理时区转换问题
1. 程序查询直接使用(java)Date即可, 因为直接支持 2. 若方便查看日期需要进行格式和时区转换 db.task.aggregate([{ $match: {userId: 113633}},{ $project: {userId: 1,endTime: 1,formattedDate: {$dateToString: {format: "%Y-%m-%d %H:%M:%S&…...

专项智能练习(定义判断)_DA_01
1. 单选题 热传导是介质内无宏观运动时的传热现象,其在固体、液体和气体中均可发生。但严格而言,只有在固体中才是纯粹的热传导,在流体(泛指液体和气体)中又是另外一种情况,流体即使处于静止状态࿰…...
