位运算题目:找到最接近目标值的函数值
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:找到最接近目标值的函数值
出处:1521. 找到最接近目标值的函数值
难度
8 级
题目描述
要求

Winston 构造了一个如上所示的函数 func \texttt{func} func。他有一个整数数组 arr \texttt{arr} arr 和一个整数 target \texttt{target} target,他想找到让 ∣ func(arr, l, r) − target ∣ \big| \texttt{func(arr, l, r)} - \texttt{target} \big| func(arr, l, r)−target 最小的 l \texttt{l} l 和 r \texttt{r} r。
返回 ∣ func(arr, l, r) − target ∣ \big| \texttt{func(arr, l, r)} - \texttt{target} \big| func(arr, l, r)−target 的最小值。
注意 func \texttt{func} func 的输入参数包含 l \texttt{l} l 和 r \texttt{r} r,满足 0 ≤ l, r < arr.length \texttt{0} \le \texttt{l, r} < \texttt{arr.length} 0≤l, r<arr.length。
示例
示例 1:
输入: arr = [9,12,3,7,15], target = 5 \texttt{arr = [9,12,3,7,15], target = 5} arr = [9,12,3,7,15], target = 5
输出: 2 \texttt{2} 2
解释:所有可能的 [l,r] \texttt{[l,r]} [l,r] 数对包括 [[0,0],[1,1],[2,2],[3,3],[4,4],[0,1],[1,2],[2,3],[3,4],[0,2],[1,3],[2,4],[0,3],[1,4],[0,4]] \texttt{[[0,0],[1,1],[2,2],[3,3],[4,4],[0,1],[1,2],[2,3],[3,4],[0,2],[1,3],[2,4],[0,3],[1,4],[0,4]]} [[0,0],[1,1],[2,2],[3,3],[4,4],[0,1],[1,2],[2,3],[3,4],[0,2],[1,3],[2,4],[0,3],[1,4],[0,4]],Winston 得到的相应结果为 [9,12,3,7,15,8,0,3,7,0,0,3,0,0,0] \texttt{[9,12,3,7,15,8,0,3,7,0,0,3,0,0,0]} [9,12,3,7,15,8,0,3,7,0,0,3,0,0,0]。最接近 5 \texttt{5} 5 的值是 7 \texttt{7} 7 和 3 \texttt{3} 3,所以最小差值为 2 \texttt{2} 2。
示例 2:
输入: arr = [1000000,1000000,1000000], target = 1 \texttt{arr = [1000000,1000000,1000000], target = 1} arr = [1000000,1000000,1000000], target = 1
输出: 999999 \texttt{999999} 999999
解释:Winston 输入函数的所有可能 [l,r] \texttt{[l,r]} [l,r] 数对得到的函数值都为 1000000 \texttt{1000000} 1000000,所以最小差值为 999999 \texttt{999999} 999999。
示例 3:
输入: arr = [1,2,4,8,16], target = 0 \texttt{arr = [1,2,4,8,16], target = 0} arr = [1,2,4,8,16], target = 0
输出: 0 \texttt{0} 0
数据范围
- 1 ≤ arr.length ≤ 10 5 \texttt{1} \le \texttt{arr.length} \le \texttt{10}^\texttt{5} 1≤arr.length≤105
- 1 ≤ arr[i] ≤ 10 6 \texttt{1} \le \texttt{arr[i]} \le \texttt{10}^\texttt{6} 1≤arr[i]≤106
- 0 ≤ target ≤ 10 7 \texttt{0} \le \texttt{target} \le \texttt{10}^\texttt{7} 0≤target≤107
解法
思路和算法
用 n n n 表示数组 arr \textit{arr} arr 的长度。如果枚举所有的下标对 ( l , r ) (l, r) (l,r),则时间复杂度至少是 O ( n 2 ) O(n^2) O(n2),该时间复杂度过高,需要优化。
如果子数组的右侧端点 r r r 固定,分别考虑两个左侧端点 l 1 l_1 l1 和 l 2 l_2 l2 对应的函数值。当 l 1 < l 2 ≤ r l_1 < l_2 \le r l1<l2≤r 时,记 v 1 = func ( arr , l 1 , r ) v_1 = \textit{func}(\textit{arr}, l_1, r) v1=func(arr,l1,r), v 2 = func ( arr , l 2 , r ) v_2 = \textit{func}(\textit{arr}, l_2, r) v2=func(arr,l2,r),则一定有 v 1 ≤ v 2 v_1 \le v_2 v1≤v2,理由如下。
对于 c = a & b c = a ~\&~ b c=a & b,考虑二进制表示的每一位,只有当 a a a 和 b b b 在同一位的值都是 1 1 1 时, c c c 在该位的值才是 1 1 1,否则 c c c 在该位的值是 0 0 0,因此 c ≤ a c \le a c≤a 且 c ≤ b c \le b c≤b。根据 func \textit{func} func 的定义有 v 1 = v 2 & ( arr [ l 1 ] & arr [ l 1 + 1 ] & … & arr [ l 2 − 1 ] ) v_1 = v_2 ~\&~ (\textit{arr}[l_1] ~\&~ \textit{arr}[l_1 + 1] ~\&~ \ldots ~\&~ \textit{arr}[l_2 - 1]) v1=v2 & (arr[l1] & arr[l1+1] & … & arr[l2−1]),利用按位与运算的性质可得 v 1 ≤ v 2 v_1 \le v_2 v1≤v2。
因此,当子数组的右侧端点固定时,当左侧端点向左移动时函数值不变或减少,当左侧端点向右移动时函数值不变或增加。当左侧端点向左移动时,函数值的二进制表示的每一位只可能不变或从 1 1 1 变成 0 0 0,不可能从 0 0 0 变成 1 1 1,因此当子数组的右侧端点 r r r 固定时,不同的函数值个数不超过 O ( log arr [ r ] ) O(\log \textit{arr}[r]) O(logarr[r])。
用 m m m 表示数组 arr \textit{arr} arr 的最大值。利用上述结论,将数组 arr \textit{arr} arr 中的每个元素作为子数组的右侧端点时只需要考虑 O ( log m ) O(\log m) O(logm) 个不同的函数值,不需要考虑 O ( n ) O(n) O(n) 个不同的函数值,可以将时间复杂度从 O ( n 2 ) O(n^2) O(n2) 降低到 O ( n log m ) O(n \log m) O(nlogm)。
具体做法是,将子数组的右侧端点初始化为 0 0 0,此时函数值为 arr [ 0 ] \textit{arr}[0] arr[0],计算 ∣ arr [ 0 ] − target ∣ \big| \textit{arr}[0] - \textit{target} \big| arr[0]−target ,作为函数值与目标值的最小差值。对于 i i i 从 1 1 1 到 n − 1 n - 1 n−1,将 i i i 作为子数组的右侧端点,当前轮的函数值包括上一轮的每个函数值分别与 arr [ i ] \textit{arr}[i] arr[i] 的按位与运算结果,以及 arr [ i ] \textit{arr}[i] arr[i],计算当前轮的每个函数值与目标值的差的绝对值,更新最小差值。
实现方面,区分上一轮的函数值和当前轮的函数值的做法有多种,可以创建两个列表分别存储上一轮的函数值和当前轮的函数值,也可以使用队列存储函数值。使用队列的做法如下。
-
当遍历到 arr [ i ] \textit{arr}[i] arr[i] 时,队列中的元素为上一轮的所有函数值,记录此时队列的大小 size \textit{size} size。
-
将 size \textit{size} size 个元素出队列,将每个出队列的元素和 arr [ i ] \textit{arr}[i] arr[i] 做按位与运算得到当前轮的函数值,将当前轮的函数值入队列。
-
最后将 arr [ i ] \textit{arr}[i] arr[i] 入队列,表示 l = r = i l = r = i l=r=i 的情况下对应的函数值。
将当前轮的函数值入队列时需要排除重复元素。由于遍历函数值的顺序具有单调性,因此相等的函数值在遍历顺序中一定相邻,每次将函数值入队列时判断当前函数值与上一个入队列的函数值是否相等,即可排除重重复元素。
代码
class Solution {public int closestToTarget(int[] arr, int target) {int minDiff = Math.abs(arr[0] - target);Queue<Integer> queue = new ArrayDeque<Integer>();queue.offer(arr[0]);int length = arr.length;for (int i = 1; i < length; i++) {int num = arr[i];int size = queue.size();int lastVal = -1;for (int j = 0; j < size; j++) {int prevVal = queue.poll();int currVal = prevVal & num;if (currVal != lastVal) {minDiff = Math.min(minDiff, Math.abs(currVal - target));queue.offer(currVal);lastVal = currVal;}}if (num != lastVal) {minDiff = Math.min(minDiff, Math.abs(num - target));queue.offer(num);}}return minDiff;}
}
复杂度分析
-
时间复杂度: O ( n log m ) O(n \log m) O(nlogm),其中 n n n 是数组 arr \textit{arr} arr 的长度, m m m 是数组 arr \textit{arr} arr 的最大值。遍历数组的过程中,对于每个元素需要 O ( log m ) O(\log m) O(logm) 的时间计算以当前元素作为结尾的所有函数值,因此时间复杂度是 O ( n log m ) O(n \log m) O(nlogm)。
-
空间复杂度: O ( log m ) O(\log m) O(logm),其中 m m m 是数组 arr \textit{arr} arr 的最大值。空间复杂度主要取决于队列,队列中的元素个数不超过 O ( log m ) O(\log m) O(logm)。
相关文章:

位运算题目:找到最接近目标值的函数值
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法思路和算法代码复杂度分析 题目 标题和出处 标题:找到最接近目标值的函数值 出处:1521. 找到最接近目标值的函数值 难度 8 级 题目描述 要求 Winston 构造了一个如上所示的函数 func \…...

哲学物理:太极图和莫比乌斯环有什么关系?
太极图 是中国传统文化中的经典符号,由阴阳两部分组成,黑白两色相互环绕,中间有两点表示阴中有阳,阳中有阴。太极图象征着对立统一、相互依存和动态平衡,是道家哲学的核心思想之一。 
机器学习笔记1
一、 机器学习介绍与定义 1. 机器学习定义 机器学习(Machine Learning)本质上就是让计算机自己在数据中学习规律,并根据所得到的规律对未来数据进行预测。 机器学习包括如聚类、分类、决策树、贝叶斯、神经网络、深度学习(Deep…...

JVM中的安全点是什么,作用又是什么?
JVM中的安全点(Safepoint) 是Java虚拟机设计中的一个关键机制,主要用于协调所有线程的执行状态,以便进行全局操作(如垃圾回收、代码反优化等)。它的核心目标是确保在需要暂停所有线程时,每个线程…...
关于github使用总结
文章目录 一、本地使用git(一)创建一个新的本地Git库首先在本地创建一个新的git仓库然后进行一次初始提交提交过后就可以查看提交记录 (二)在本地仓库进行版本恢复先执行 git log 查看项目提交历史使用 git checkout 恢复版本 二、…...

基于Qt6 + MuPDF在 Arm IMX6ULL运行的PDF浏览器——MuPDF Adapter文档
项目地址:总项目Charliechen114514/CCIMXDesktop: This is a Qt Written Desktop with base GUI Utilities 本子项目地址:CCIMXDesktop/extern_app/pdfReader at main Charliechen114514/CCIMXDesktop 前言 这个部分说的是Mupdf_adaper下的文档的工…...

google-Chrome常用插件
google-Chrome常用插件 1. json格式化展示插件 github下载jsonview-for-chrome插件 通过离线安装方式 拓展程序-》管理拓展程序-》打开开发者模式-》加载已解压的拓展程序-》选择拓展程序解压的位置 2. 翻译插件 插件下载地址:Immersive Translate - Bilingual …...

2024年9月电子学会等级考试五级第三题——整数分解
题目 3、整数分解 正整数 N 的 K-P 分解是指将 N 写成 K 个正整数的 P 次方的和。本题就请你对任意给定的正整数 N、K、P,写出 N 的 K-P 分解。 时间限制:8000 内存限制:262144 输入 输入在一行给出 3 个正整数 N (≤ 400)、K (≤ N)、P (1 …...

毕设设计 | 管理系统图例
文章目录 环素1. 登录、注册2. 菜单管理 环素 1. 登录、注册 2. 菜单管理 公告通知 订单管理 会员管理 奖品管理 新增、编辑模块...

u3d 定义列表详细过程
层级结构 - Canvas - Scroll View - Viewport - Content (Vertical Layout Group) - Item1 (Prefab) - Item2 (Prefab) ... 详细设置步骤 1. 创建 Canvas 2. 添加 Scroll View 组件 3. 在 Scroll View 下创建 Content 子对象 4. 添加 …...
进行性能分析)
使用 `perf` 和火焰图(Flame Graph)进行性能分析
在现代软件开发中,性能优化是提升应用程序响应速度和资源利用率的关键步骤。当一个进程的 CPU 占用率异常高时,识别并优化性能瓶颈显得尤为重要。本文将详细介绍如何使用 Linux 下强大的性能分析工具 perf 以及火焰图(Flame Graph)…...

什么情况会导致JVM退出?
大家好,我是锋哥。今天分享关于【什么情况会导致JVM退出?】面试题。希望对大家有帮助; 什么情况会导致JVM退出? 1000道 互联网大厂Java工程师 精选面试题-Java资源分享网 JVM(Java虚拟机)退出的情况通常是…...

实验6 电子邮件
实验6 电子邮件 1、实验目的 理解电子邮件系统基本结构 理解客户端和服务器端,以及服务器之间的通信 分析理解SMTP,POP3协议 2、实验环境 硬件要求:阿里云云主机ECS 一台。 软件要求:Linux/ Windows 操作系统 3、实验内容…...

AI大模型从0到1记录学习numpy pandas day24
第 1 章 环境搭建 1.1 Anaconda 1.1.1 什么是Anaconda Anaconda官网地址:https://www.anaconda.com/ 简单来说,Anaconda Python 包和环境管理器(Conda) 常用库 集成工具。它适合那些需要快速搭建数据科学或机器学习开发环境的用…...

深入理解浏览器渲染引擎:底层机制与性能优化实战
现代浏览器背后是一个庞大而复杂的系统工程,渲染引擎作为核心模块之一,承担着从解析 HTML/CSS 到最终绘制页面的关键职责。本文将从底层机制出发,系统梳理渲染引擎(如 Blink)工作原理、V8 与渲染流程的协作方式&#x…...
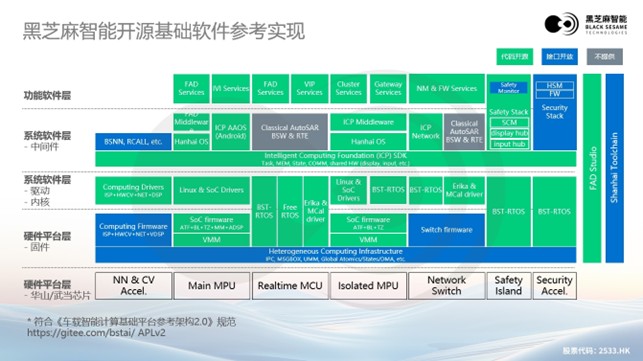
大模型浪潮下,黑芝麻智能高性能芯片助力汽车辅助驾驶变革
在全球汽车产业向智能化、网联化加速转型的浪潮中,大模型技术的崛起为汽车领域带来了前所未有的变革机遇。黑芝麻智能在高性能芯片和基础软件架构领域的持续创新,正全力推动汽车智能化的发展,为行业注入新的活力。 大模型全面助力辅助驾驶迈…...

鸿蒙OSUniApp制作多选框与单选框组件#三方框架 #Uniapp
使用UniApp制作多选框与单选框组件 前言 在移动端应用开发中,表单元素是用户交互的重要组成部分。尤其是多选框(Checkbox)和单选框(Radio),它们几乎存在于每一个需要用户做出选择的场景中。虽然UniApp提供…...
康谋分享 | 自动驾驶仿真进入“标准时代”:aiSim全面对接ASAM OpenX
目录 一、OpenDRIVE:兼容多版本地图标准 (1)Atlas 工作流 (2)UE Plugin 工作流 二、OpenSCENARIO:标准化动态行为建模 三、OpenCRG:还原毫米级路面细节 四、OpenMATERIAL:更真…...

VMware中快速安装与优化Ubuntu全攻略
准备工作 在开始安装之前,确保已经下载了VMware Workstation或VMware Player,并准备好Ubuntu的ISO镜像文件。VMware Workstation是一款功能强大的虚拟机软件,支持在Windows或Linux主机上运行多个操作系统。 创建虚拟机 打开VMware Worksta…...

GPUGeek云平台实战:DeepSeek-R1-70B大语言模型一站式部署
随着人工智能技术的迅猛发展,特别是在自然语言处理领域,大型语言模型如DeepSeek-R1-70B的出现,推动了各行各业的变革。为了应对这些庞大模型的计算需求,云计算平台的普及成为了关键,特别是基于GPU加速的云平台…...

无人机动力系统全解析:核心组件、工作原理与实用指南
无人机想要实现稳定飞行与灵活操控,离不开一套高效协同的动力系统。该系统以电机、电子调速器(电调)、电池和螺旋桨四大核心组件为基础,各部分精密配合,共同驱动无人机翱翔蓝天。接下来,本文将从基础原理入…...

【C语言】初阶数据结构相关习题(二)
🎆个人主页:夜晚中的人海 今日语录:知识是从刻苦劳动中得来的,任何成就都是刻苦劳动的结果。——宋庆龄 文章目录 🎄一、链表内指定区间翻转🎉二、从链表中删去总和值为零的节点🚀三、链表求和&…...

嵌入式学习--江科大51单片机day7
我们在听课的过程中,可能对老师讲的有疑问,或者有些自己的理解,我们可以去问豆包,包括在写博客的时候我也是,不断去问豆包保证思考的正确性。(有人感觉豆包很low啊,其实这些基础性的东西豆包一般…...

基于大模型预测围术期麻醉苏醒时间的技术方案
目录 一、数据收集与处理(一)数据来源(二)数据预处理二、大模型构建与训练(一)模型选择(二)模型训练三、围术期麻醉苏醒时间预测(一)术前预测(二)术中动态预测四、并发症风险预测(一)风险因素分析(二)风险预测模型五、基于预测制定手术方案(一)个性化手术规划…...

Element Plus 取消el-form-item点击触发组件,改为原生表单控件
文章目录 问题:方法一:使用全局样式覆盖(推荐)方法二:自定义指令(更灵活)方法三:封装高阶组件方法四:运行时DOM修改(不推荐) 问题: 描…...

javascript —— ! 和 !! 的区别与作用
javascript —— ! 和 !! 的区别与作用 在 JavaScript 里,! 和 !! 是两种不同的逻辑运算符,它们的功能和使用场景有明显区别。 1、 !(逻辑非运算符) 它的主要作用是 对操作数进行布尔值取反。具体来说,就是 先把操作…...

鸿蒙 ArkUI - ArkTS 组件 官方 UI组件 合集
ArkUI 组件速查表 鸿蒙应用开发页面上需要实现的 UI 功能组件如果在这 100 多个组件里都找不到,那就需要组合造轮子了 使用技巧:先判断需要实现的组件大方向,比如“选择”、“文本”、“信息”等,或者是某种形状比如“块”、“图…...
位置编码(1))
LLM笔记(三)位置编码(1)
位置编码理论与应用 1. 位置编码如何解决置换不变性及其数学表现 在Transformer模型中,自注意力机制(Self-Attention)具有置换不变性(permutation invariance),这意味着对输入序列的词元(toke…...

麒麟v10 部署 MySQL 5.6.10 完整步骤
需要包的私信我 一、安装依赖(Perl环境) # 在线安装依赖 yum -y install perl perl-devel# 离线安装(需提前下载好rpm包) mkdir /data/ybn/soft/pre yum install --downloadonly --downloaddir/data/ybn/soft/pre perl perl-dev…...

Git-学习笔记(粗略版)
前言 很多人都听过git,github这些名词,但是它们是什么,怎么使用?git和github是一个东西吗?本文将详细解答这些问题,彻底弄懂git。 1.Git是啥❓ 有一天,我们的插画师小王接到一个绘画订单,但奈…...
