对称二叉树的判定:双端队列的精妙应用
一、题目解析
题目描述
给定一个二叉树,检查它是否是镜像对称的。例如,二叉树 [1,2,2,3,4,4,3] 是对称的:
1/ \2 2/ \ / \
3 4 4 3
而 [1,2,2,null,3,null,3] 则不是镜像对称的:
1/ \2 2\ \3 3
问题本质
判断一棵二叉树是否镜像对称,等价于判断其左子树和右子树是否互为镜像。具体来说,需要满足以下条件:
- 根节点的值相同
- 每个树的左子树与另一个树的右子树镜像对称
二、双端队列解法思路
核心思想
使用双端队列(Deque)同时存储待比较的节点对,通过队列两端的操作,确保每次取出的节点对是需要比较的镜像节点。具体步骤如下:
- 将根节点的左右子节点分别从队列的前端和后端入队
- 每次循环从队列两端各取出一个节点进行比较
- 若两节点均为空,继续循环
- 若两节点中只有一个为空或值不相等,返回
false - 若两节点均非空且值相等,将它们的子节点按镜像关系入队:
- 左子树的左节点与右子树的右节点入队
- 左子树的右节点与右子树的左节点入队
代码实现
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean isSymmetric(TreeNode root) {Deque<TreeNode> cur = new LinkedList<>();if (root == null) {return true;}TreeNode tempLeft = root.left;TreeNode tempRight = root.right;cur.offerFirst(tempLeft);cur.offerLast(tempRight);while (!cur.isEmpty()) {tempLeft = cur.pollFirst();tempRight = cur.pollLast();if (tempLeft == null && tempRight == null) {continue;}if (tempLeft == null || tempRight == null || tempLeft.val != tempRight.val) {return false;}cur.offerFirst(tempLeft.left);cur.offerFirst(tempLeft.right);cur.offerLast(tempRight.right);cur.offerLast(tempRight.left);}return true;}
}
三、代码详细解释
初始化与边界处理
Deque<TreeNode> cur = new LinkedList<>();
if (root == null) {return true;
}
TreeNode tempLeft = root.left;
TreeNode tempRight = root.right;
cur.offerFirst(tempLeft);
cur.offerLast(tempRight);
- 创建双端队列
cur用于存储待比较的节点对 - 若根节点为空,直接返回
true(空树视为对称) - 将根节点的左右子节点分别从队列的前端和后端入队
主循环处理
while (!cur.isEmpty()) {tempLeft = cur.pollFirst();tempRight = cur.pollLast();if (tempLeft == null && tempRight == null) {continue;}if (tempLeft == null || tempRight == null || tempLeft.val != tempRight.val) {return false;}// 处理子节点
}
- 每次循环从队列前端和后端各取出一个节点
- 若两节点均为空,跳过当前循环
- 若两节点中只有一个为空或值不相等,说明不对称,返回
false
子节点处理
cur.offerFirst(tempLeft.left);
cur.offerFirst(tempLeft.right);
cur.offerLast(tempRight.right);
cur.offerLast(tempRight.left);
- 将左子树的左节点和右节点依次从队列前端入队
- 将右子树的右节点和左节点依次从队列后端入队
- 这样确保了下一次循环时,左子树的左节点会与右子树的右节点比较,左子树的右节点会与右子树的左节点比较
四、算法示例演示
以对称二叉树 [1,2,2,3,4,4,3] 为例,展示队列的变化过程:
初始状态
队列: [2, 2]
第一次循环
- 取出
2和2 - 值相等,处理子节点:
- 左子树的左节点
3入队首 - 左子树的右节点
4入队首 - 右子树的右节点
3入队尾 - 右子树的左节点
4入队尾
- 左子树的左节点
队列: [3, 4, 4, 3]
第二次循环
- 取出
3和3 - 值相等,无子节点,队列变为
[4, 4]
第三次循环
- 取出
4和4 - 值相等,无子节点,队列为空
- 返回
true
五、复杂度分析
- 时间复杂度:O(n),每个节点仅被访问一次
- 空间复杂度:O(h),h为树的高度,最坏情况下为O(n)
六、双端队列的优势
使用双端队列的关键在于能够同时维护两个方向的节点对,通过以下操作实现镜像比较:
offerFirst()和pollFirst()处理左子树节点offerLast()和pollLast()处理右子树节点- 这种设计使得每次取出的节点对恰好是需要比较的镜像节点,避免了递归或单队列方法中的额外处理逻辑
七、总结
双端队列解法通过巧妙的入队和出队策略,将镜像比较的逻辑转化为队列两端的操作,既保持了迭代方法的优势(避免栈溢出),又直观地实现了节点对的比较。理解这种解法的关键在于把握队列操作与镜像关系的对应:
- 左子树的左节点 → 队列前端
- 左子树的右节点 → 队列前端
- 右子树的右节点 → 队列后端
- 右子树的左节点 → 队列后端
这种对称性的设计使得代码简洁高效,是解决对称二叉树问题的一种优雅方式。
相关文章:

对称二叉树的判定:双端队列的精妙应用
一、题目解析 题目描述 给定一个二叉树,检查它是否是镜像对称的。例如,二叉树 [1,2,2,3,4,4,3] 是对称的: 1/ \2 2/ \ / \ 3 4 4 3而 [1,2,2,null,3,null,3] 则不是镜像对称的: 1/ \2 2\ \3 3问题本质 判断一棵二叉…...

使用Python实现简单的人工智能聊天机器人
最近研学过程中发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击链接跳转到网站人工智能及编程语言学习教程。读者们可以通过里面的文章详细了解一下人工智能及其编程等教程和学习方法。下面开始对正文内容的…...

React 播客专栏 Vol.11|Plain CSS 如何在 React 中优雅登场?
👋 欢迎回到《前端达人 React 播客书单》第 11 期(正文内容为学习笔记摘要,音频内容是详细的解读,方便你理解),请点击下方收听 今天我们进入前端样式化的第一课,用最传统的方式 —— Plain CSS…...

css:倒影倾斜效果
这是需要实现的效果,平时用的比较多的是添加阴影,是box-shadow,而添加倒影是box-reflect,需要注意的是box-reflect需要添加浏览器前缀,比如我用的谷歌浏览器,要加-webkit-才能生效。 -webkit-box-reflect:…...

spring学习->sprintboot
spring IoC(控制翻转): 控制:资源的控制权(资源的创建,获取,销毁等) 反转:和传统方式不一样(用上面new什么),不用new让ioc来发现你用什么,然后我来给什么 DI:(依赖注入) 依赖:组件的依赖关系。如newsController依赖NewsServi…...

语音识别——通过PyAudio录入音频
PyAudio 是一个用于处理音频的 Python 库,它提供了录制和播放音频的功能。通过 PyAudio,可以轻松地从麦克风或其他音频输入设备录制音频,并将其保存为文件或进行进一步处理。 安装 PyAudio 在使用 PyAudio 之前,需要先安装它。可…...

五月月报丨MaxKB在教育行业的应用进展与典型场景
在2025年的3月和4月的“用户应用月度报告”中,MaxKB开源项目组相继总结了MaxKB开源项目在政府、公共事业、教育、医疗以及企事业单位的应用情况。毫无疑问,在DeepSeek等国产大模型被各行各业的用户广泛接受之后,AI应用建设并运营的步伐也在显…...

算法练习:JZ51 数组中的逆序对
分析: 题干两个坑: 数组长度最大 1 0 5 10^5 105; P的值可能超过整型数据范围; 作为归并排序的变式。 为什么能用归并排序找到逆序对?因为归并排序的重组步骤中,左数组与右数组是有序的,对…...

【流程控制结构】
流程控制结构 流程控制结构1、顺序结构2、选择结构if基本选择结构if else语法多重if语法嵌套if语法switch选择结构 3、循环结构循环结构while循环结构程序调试for循环跳转语句区别 流程控制结构 1、顺序结构 流程图 优先级 2、选择结构 if基本选择结构 单if 语法 if&…...

掌握 Kotlin Android 单元测试:MockK 框架深度实践指南
掌握 Kotlin Android 单元测试:MockK 框架深度实践指南 在 Android 开发中,单元测试是保障代码质量的核心手段。但面对复杂的依赖关系和 Kotlin 语言特性,传统 Mock 框架常显得力不从心。本文将带你深入 MockK —— 一款专为 Kotlin 设计的 …...

嵌入式故障码管理系统设计实现
文章目录 前言一、故障码管理系统概述二、核心数据结构设计2.1 故障严重等级定义2.2 模块 ID 定义2.3 故障代码结构2.4 故障记录结构 三、故障管理核心功能实现3.1 初始化功能3.2 故障记录功能3.3 记录查询与清除功能3.4 系统自检功能 四、故障存储实现4.1 Flash 存储实现4.2 R…...

PowerBI基础
一、前言 在当今数据驱动的时代,如何高效地整理、分析并呈现数据,已成为企业和个人提升决策质量的关键能力。Power BI 作为微软推出的强大商业智能工具,正帮助全球用户将海量数据转化为直观、动态的可视化洞察。数据的世界充满可能性…...

一文了解多模态大模型LLaVA与LLaMA的概念
目录 一、引言 二、LLaVA与LLaMA的定义 2.1 LLaMA 2.2 LLaVA 2.3 LLaVA-NeXT 的技术突破 三、产生的背景 3.1 LLaMA的背景 3.2 LLaVA的背景 四、与其他竞品的对比 4.1 LLaMA的竞品 4.2 LLaVA的竞品 五、应用场景 5.1 LLaMA的应用场景 5.2 LLaVA的应用场景 六…...

E-R图合并时的三种冲突
属性冲突 属性冲突指的是在合并两个实体时,相同属性的数据类型、取值范围或约束条件不一致。例如,一个实体中的“年龄”属性定义为整数类型,而另一个实体中的“年龄”属性定义为字符串类型,这就产生了属性冲突。 命名冲突 命名…...

原生小程序+springboot+vue+协同过滤算法的音乐推荐系统(源码+论文+讲解+安装+部署+调试)
感兴趣的可以先收藏起来,还有大家在毕设选题,项目以及论文编写等相关问题都可以给我留言咨询,我会一一回复,希望帮助更多的人。 系统背景 在数字音乐产业迅猛发展的当下,Spotify、QQ 音乐、网易云音乐等音乐平台的曲…...

【MySQL】项目实践
个人主页:Guiat 归属专栏:MySQL 文章目录 1. 项目实践概述1.1 项目实践的重要性1.2 项目中MySQL的典型应用场景 2. 数据库设计流程2.1 需求分析与规划2.2 设计过程示例2.3 数据库设计工具 3. 电子商务平台实践案例3.1 系统架构3.2 数据库Schema设计3.3 数…...

windows下authas调试tomcat
一般情况下,我们只需要输入以下代码 java -jar authas.jar调试tomcat时需要加上进程号 java -jar authas.jar <PID> 此外,如果你使用的是 Java 11 或更高版本,你需要添加 --add-opens 参数,以便 Arthas 能够访问 JVM 的内…...

回调函数应用示例
回调函数是一种通过函数指针(或引用)调用的函数,它在特定事件或条件发生时被另一个函数调用。回调函数的核心思想是将函数作为参数传递,以便在适当的时候执行自定义逻辑,常用于异步编程、事件驱动架构等场景。 业务场景…...
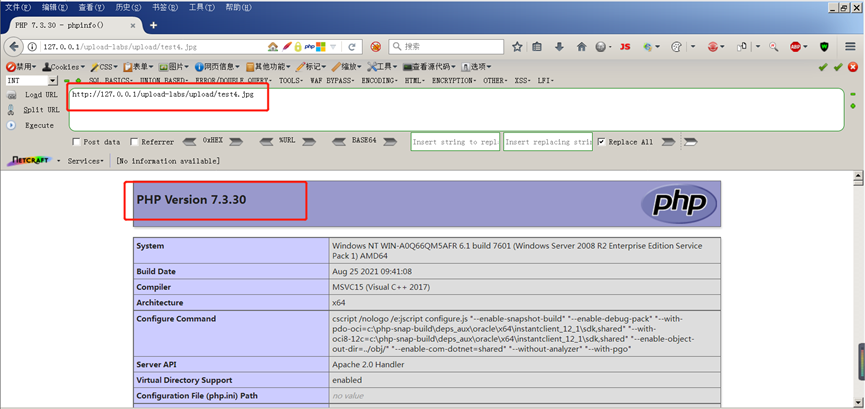
upload-labs通关笔记-第4关 文件上传之.htacess绕过
目录 一、.htacess 二、代码审计 三、php ts版本安装 1、下载ts版本php 2、放入到phpstudy指定文件夹中 3、修改php配置文件 4、修改php.ini文件 5、修改httpd.conf文件 (1)定位文件 (2)修改文件 6、重启小皮 7、切换…...

DeepSearch代表工作
介绍下今年以来深度搜索相关的一些论文~ 文章目录 Search-o1简述方法实验Search-R1简介方法带搜索引擎的强化学习多轮搜索调用的生成训练模板奖励建模实验R1-Searcher简介方法数据选择两阶段的强化学习训练算法ReSearch: Learning to Reason with Search for LLMs via Reinforc…...

记录一次服务器卡顿
一、服务器卡顿现象 服务用了一段时间后,突然很卡,发现在服务器上新建excel也很卡,发现服务器中病毒了,然后重新安装了操作系统。重新安装服务环境时,发现同时安装pdf、tomcat时都很慢,只能一个安装好了&am…...

C++ 中的几种锁机制整理
1. 互斥锁(std::mutex) ✅ 简介 最常用的线程同步工具。保证同一时间只能有一个线程访问临界区。 ✅ 使用方式 #include <mutex>std::mutex mtx;void safeFunction() {std::lock_guard<std::mutex> lock(mtx);// 临界区代码 }✅ 优点 简…...

leetcode2749. 得到整数零需要执行的最少操作数-medium
1 题目:得到整数零需要执行的最少操作数 官方标定难度:中 给你两个整数:num1 和 num2 。 在一步操作中,你需要从范围 [0, 60] 中选出一个整数 i ,并从 num1 减去 2i num2 。 请你计算,要想使 num1 等于…...

14 C 语言浮点类型详解:类型精度、表示形式、字面量后缀、格式化输出、容差判断、存储机制
1 浮点类型 1.1 浮点类型概述 浮点类型用于表示小数(如 123.4、3.1415、0.99),支持正数、负数和零,是科学计算和工程应用的核心数据类型。 1.2 浮点数的类型与规格 浮点类型存储大小值范围(近似)实际有效…...

Java 多线程基础:Thread 类核心用法详解
一、线程创建 1. 继承 Thread 类(传统写法) class MyThread extends Thread { Override public void run() { System.out.println("线程执行"); } } // 使用示例 MyThread t new MyThread(); t.start(); 缺点:Java 单…...

Vue3:脚手架
工程环境配置 1.安装nodejs 这里我已经安装过了,只需要打开链接Node.js — Run JavaScript Everywhere直接下载nodejs,安装直接一直下一步下一步 安装完成之后我们来使用电脑的命令行窗口检查一下版本 查看npm源 这里npm源的地址是淘宝的源࿰…...

显性知识的主要特征
有4个主要特征: 客观存在性静态存在性可共享性认知元能性...

使用pytest实现参数化后,控制台输出的日志是乱码
测试用例id显示的是乱码 问题 testcases/test_测试用例.py::TestPro::test_测试用例_用例1**[\u5fc3\u453g2]** PASSED [ 33%] 要让 pytest 在参数化测试中正确显示中文用例名称而非 Unicode 转义字符,可以通过以下两种方法 解决: 全局禁用测试 ID …...

自定义快捷键软件:AutoHotkey 高效的快捷键执行脚本软件
AutoHotkey 是一种适用于 Windows 的免费开源脚本语言,它允许用户轻松创建从小型到复杂的脚本,用于各种任务,例如:表单填充、自动点击、宏等。 定义鼠标和键盘的热键,重新映射按键或按钮,并进行类似自动更…...

【C++】 —— 笔试刷题day_30
一、爱吃素 题目解析 这道题,简单来说就是给定两个数a和b,然后让我们判断a*b是否是素数。 算法思路 这道题还是比较简单的 首先,输入两个数a和b,这两个数的数据范围都是[1, 10^11];10的11次方,那a*b不就是…...
