mathematics-2024《Graph Convolutional Network for Image Restoration: A Survey》
推荐深蓝学院的《深度神经网络加速:cuDNN 与 TensorRT》,课程面向就业,细致讲解CUDA运算的理论支撑与实践,学完可以系统化掌握CUDA基础编程知识以及TensorRT实战,并且能够利用GPU开发高性能、高并发的软件系统,感兴趣可以直接看看链接:深蓝学院《深度神经网络加速:cuDNN 与 TensorRT》

核心思想
该论文的核心思想是系统性地综述了图卷积网络(Graph Convolutional Networks, GCNs)在图像修复(image restoration)领域的应用,重点探讨了GCNs在图像去噪(image denoising)、超分辨率(image super-resolution)和去模糊(image deblurring)等任务中的潜力与优势。论文强调了GCNs在处理非欧几里得数据结构(如图像的像素关系图)方面的独特能力,特别是其能够捕捉图像中的长距离依赖(long-range dependencies)并保留局部结构信息,从而提升修复效果。论文通过对比传统方法(如基于滤波和基于模型的方法)与基于学习的GCN方法,展示了GCNs在复杂图像修复任务中的优越性,并指出了未来的研究方向和挑战。
目标函数
在图像修复任务中,GCNs的目标函数通常设计为最小化修复图像与真实清晰图像之间的差异,同时考虑图像的拓扑结构信息。具体来说,目标函数可以分为以下几类:
-
图像去噪目标函数:
对于去噪任务,目标函数通常基于均方误差(Mean Squared Error, MSE)或结构相似性(Structural Similarity, SSIM)等指标,结合GCNs的图结构特性。例如,论文中提到的AdarGCN和CP-GCN等方法的目标函数可以表示为:
L = 1 N ∑ i = 1 N ∥ I ^ i − I i ∥ 2 2 + λ R ( G ) , \mathcal{L} = \frac{1}{N} \sum_{i=1}^N \left\| \hat{I}_i - I_i \right\|_2^2 + \lambda \mathcal{R}(\mathcal{G}), L=N1i=1∑N I^i−Ii 22+λR(G),
其中:- I ^ i \hat{I}_i I^i 表示GCN预测的去噪图像像素值, I i I_i Ii 为对应的真实清晰图像像素值。
- R ( G ) \mathcal{R}(\mathcal{G}) R(G) 是正则化项,基于图结构 G \mathcal{G} G(包括节点和边信息),用于约束图的拓扑特性或防止过拟合。
- λ \lambda λ 是正则化权重。
-
超分辨率目标函数:
对于超分辨率任务,目标函数旨在最小化低分辨率图像经过GCN上采样后的输出与高分辨率真实图像之间的差异。例如,GCEDSR方法的目标函数可能为:
L = 1 N ∑ i = 1 N ∥ GCN ( I i L R ) − I i H R ∥ 2 2 + μ L perceptual , \mathcal{L} = \frac{1}{N} \sum_{i=1}^N \left\| \text{GCN}(I^{LR}_i) - I^{HR}_i \right\|_2^2 + \mu \mathcal{L}_{\text{perceptual}}, L=N1i=1∑N GCN(IiLR)−IiHR 22+μLperceptual,
其中:- I i L R I^{LR}_i IiLR 和 I i H R I^{HR}_i IiHR 分别为低分辨率输入和高分辨率目标图像。
- L perceptual \mathcal{L}_{\text{perceptual}} Lperceptual 是感知损失(perceptual loss),基于预训练网络(如VGG)提取的高级特征差异。
- μ \mu μ 是感知损失的权重。
-
去模糊目标函数:
去模糊任务的目标函数通常结合像素级损失和结构级损失。例如,WIG-Net方法的目标函数可能为:
L = ∥ I ^ − I ∥ 2 2 + γ L gradient + η L graph , \mathcal{L} = \left\| \hat{I} - I \right\|_2^2 + \gamma \mathcal{L}_{\text{gradient}} + \eta \mathcal{L}_{\text{graph}}, L= I^−I 22+γLgradient+ηLgraph,
其中:- L gradient \mathcal{L}_{\text{gradient}} Lgradient 是梯度损失,鼓励恢复图像保留清晰的边缘信息。
- L graph \mathcal{L}_{\text{graph}} Lgraph 是基于图结构的损失,约束GCN输出的拓扑一致性。
- γ \gamma γ 和 η \eta η 是权重参数。
目标函数的优化过程
GCNs的目标函数优化通常通过梯度下降法或其变种(如Adam优化器)实现,结合图结构的特性进行迭代更新。优化过程包括以下步骤:
-
图结构构建:
- 将图像表示为图 G = ( V , E ) \mathcal{G} = (V, E) G=(V,E),其中节点 V V V 表示像素或图像块,边 E E E 表示像素间的关系(如邻接关系或特征相似性)。
- 使用邻接矩阵 A A A 表示边权重,归一化后的形式为 D ~ − 1 2 A ~ D ~ − 1 2 \tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} D~−21A~D~−21,其中 A ~ = A + I N \tilde{A} = A + I_N A~=A+IN(加入自环), D ~ \tilde{D} D~ 为度矩阵。
-
特征传播与聚合:
- GCN通过消息传递机制更新节点特征。每一层的特征更新公式为:
H ( l + 1 ) = σ ( D ~ − 1 2 A ~ D ~ − 1 2 H ( l ) W ( l ) ) , H^{(l+1)} = \sigma \left( \tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} H^{(l)} W^{(l)} \right), H(l+1)=σ(D~−21A~D~−21H(l)W(l)),
其中 H ( l ) H^{(l)} H(l) 是第 l l l 层的节点特征矩阵, W ( l ) W^{(l)} W(l) 是可学习的权重矩阵, σ \sigma σ 是激活函数(如ReLU)。
- GCN通过消息传递机制更新节点特征。每一层的特征更新公式为:
-
损失计算:
- 根据目标函数(如MSE、感知损失或图结构损失),计算当前预测输出与真实图像之间的损失。
-
反向传播与参数更新:
- 通过自动微分计算损失对网络参数(包括权重矩阵 W ( l ) W^{(l)} W(l) 和图结构相关参数)的梯度。
- 使用优化器(如Adam)更新参数:
θ ← θ − η ∇ θ L , \theta \leftarrow \theta - \eta \nabla_{\theta} \mathcal{L}, θ←θ−η∇θL,
其中 η \eta η 是学习率, ∇ θ L \nabla_{\theta} \mathcal{L} ∇θL 是损失对参数的梯度。
-
迭代优化:
- 重复上述步骤直到损失收敛或达到预设的迭代次数。
主要贡献点
该论文的主要贡献点包括:
-
系统性综述:
- 提供了GCNs在图像修复领域的全面综述,涵盖图像去噪、超分辨率和去模糊三大任务,填补了相关领域综述的空白。
-
方法分类与分析:
- 将GCN方法分类为图像去噪、超分辨率、去模糊以及与大模型(LLMs)结合的方法,并分析了每类方法的动机、原理和性能。
-
性能比较:
- 通过公开数据集(如Set5、Set14、Urban100、BSD100)对GCN方法与传统方法进行了定量和定性比较,展示了GCN在捕捉长距离依赖和提升图像质量方面的优越性。
-
未来方向与挑战:
- 提出了GCN在图像修复中的潜在研究方向(如网络优化、多模态融合、轻量化设计)和挑战(如图结构构建、计算成本、泛化能力),为后续研究提供了指导。
实验结果
论文通过在标准数据集上进行实验,比较了GCN方法与传统方法的性能。以下是关键实验结果的总结:
-
图像去噪:
- 在BSD68和Set12数据集上,GCN方法(如AdarGCN、CP-GCN、GAiA-Net)在峰值信噪比(PSNR)和SSIM指标上优于传统方法(如BM3D)和CNN基方法(如DnCNN)。
- 例如,CP-GCN在BSD68数据集上针对高斯噪声( σ = 50 \sigma=50 σ=50)的PSNR达到28.45 dB,优于DnCNN的28.01 dB。
-
超分辨率:
- 在Set5、Set14、Urban100和BSD100数据集上,GCEDSR方法在不同放大倍数( × 2 , × 4 , × 8 \times 2, \times 4, \times 8 ×2,×4,×8)下表现出色。例如,在Set5数据集上,GCEDSR在 × 4 \times 4 ×4放大倍数的PSNR为32.61 dB,SSIM为0.9001,优于EDSR(32.46 dB / 0.8968)。
- 随着放大倍数增加,所有方法的性能下降,但GCN方法在恢复高频细节方面更具优势。
-
去模糊:
- 在GoPro数据集上,WIG-Net等GCN方法在PSNR和SSIM上优于传统去模糊方法(如DeblurGAN)。例如,WIG-Net的PSNR达到30.12 dB,优于DeblurGAN的29.55 dB。
- GCN方法在处理复杂运动模糊时表现出更好的结构保留能力。
-
综合分析:
- GCN方法在捕捉长距离依赖和复杂拓扑结构方面优于CNN方法,尤其是在处理非均匀噪声或复杂场景时。
- 定性结果显示,GCN方法生成的图像在纹理细节和结构完整性上更接近真实图像。
算法实现过程
以下以图像去噪任务中的AdarGCN方法为例,详细解释GCN算法的实现过程:
-
输入准备:
- 输入为噪声图像 I noisy ∈ R H × W × C I_{\text{noisy}} \in \mathbb{R}^{H \times W \times C} Inoisy∈RH×W×C,其中 H H H、 W W W 为图像高宽, C C C 为通道数。
- 将图像分割为像素或图像块,构造图 G = ( V , E ) \mathcal{G} = (V, E) G=(V,E),其中节点 V V V 表示像素/块,边 E E E 根据像素间的空间距离或特征相似性定义。
- 计算邻接矩阵 A A A,通常基于k近邻算法(k-NN)或余弦相似性:
A i j = { exp ( − ∥ f i − f j ∥ 2 2 σ 2 ) , if j ∈ N i , 0 , otherwise , A_{ij} = \begin{cases} \exp\left(-\frac{\|f_i - f_j\|_2^2}{\sigma^2}\right), & \text{if } j \in \mathcal{N}_i, \\ 0, & \text{otherwise}, \end{cases} Aij={exp(−σ2∥fi−fj∥22),0,if j∈Ni,otherwise,
其中 f i f_i fi 和 f j f_j fj 是节点 i i i 和 j j j 的特征向量, N i \mathcal{N}_i Ni 是节点 i i i 的邻居集。
-
GCN网络架构:
- 初始化:将输入图像的像素特征(或提取的CNN特征)作为节点特征矩阵 H ( 0 ) ∈ R N × F H^{(0)} \in \mathbb{R}^{N \times F} H(0)∈RN×F,其中 N N N 是节点数, F F F 是特征维度。
- GCN层:堆叠多个GCN层,每层执行特征聚合和变换:
H ( l + 1 ) = σ ( D ~ − 1 2 A ~ D ~ − 1 2 H ( l ) W ( l ) ) , H^{(l+1)} = \sigma \left( \tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} H^{(l)} W^{(l)} \right), H(l+1)=σ(D~−21A~D~−21H(l)W(l)),
其中 A ~ = A + I N \tilde{A} = A + I_N A~=A+IN, D ~ \tilde{D} D~ 是度矩阵, W ( l ) ∈ R F l × F l + 1 W^{(l)} \in \mathbb{R}^{F_l \times F_{l+1}} W(l)∈RFl×Fl+1 是权重矩阵。 - 自适应聚合:AdarGCN引入自适应权重机制,动态调整邻接矩阵 A A A:
A ′ = Softmax ( MLP ( [ H i ( l ) , H j ( l ) ] ) ) , A' = \text{Softmax} \left( \text{MLP} \left( [H^{(l)}_i, H^{(l)}_j] \right) \right), A′=Softmax(MLP([Hi(l),Hj(l)])),
其中 MLP \text{MLP} MLP 是一个多层感知机, [ H i ( l ) , H j ( l ) ] [H^{(l)}_i, H^{(l)}_j] [Hi(l),Hj(l)] 是节点对的特征拼接。
-
输出层:
- 最后一层GCN输出节点特征 H ( L ) H^{(L)} H(L),通过全连接层或卷积层映射回图像空间,生成去噪图像 I ^ \hat{I} I^:
I ^ = Conv ( H ( L ) ) . \hat{I} = \text{Conv} \left( H^{(L)} \right). I^=Conv(H(L)).
- 最后一层GCN输出节点特征 H ( L ) H^{(L)} H(L),通过全连接层或卷积层映射回图像空间,生成去噪图像 I ^ \hat{I} I^:
-
损失函数:
- 使用MSE损失计算预测图像与真实图像的差异:
L = 1 N ∑ i = 1 N ∥ I ^ i − I i ∥ 2 2 . \mathcal{L} = \frac{1}{N} \sum_{i=1}^N \left\| \hat{I}_i - I_i \right\|_2^2. L=N1i=1∑N I^i−Ii 22. - 可选地加入正则化项,如图平滑损失:
L graph = ∑ i , j A i j ∥ H i − H j ∥ 2 2 . \mathcal{L}_{\text{graph}} = \sum_{i,j} A_{ij} \left\| H_i - H_j \right\|_2^2. Lgraph=i,j∑Aij∥Hi−Hj∥22.
- 使用MSE损失计算预测图像与真实图像的差异:
-
训练过程:
- 使用Adam优化器,设置学习率(如 1 0 − 3 10^{-3} 10−3),批量大小(如32)。
- 在训练集(如BSD68)上迭代优化,验证集上监控PSNR和SSIM。
- 提前停止或学习率调度以防止过拟合。
-
测试与评估:
- 在测试集(如Set12)上评估模型,计算PSNR、SSIM等指标。
- 定性分析输出图像的纹理和结构恢复效果。
总结
该论文通过系统综述和实验验证,展示了GCNs在图像修复领域的强大潜力,尤其是在处理复杂像素关系和长距离依赖方面的优势。其目标函数结合像素级损失和图结构约束,通过梯度下降优化实现高效训练。实验结果表明,GCN方法在去噪、超分辨率和去模糊任务中均优于传统方法,为未来研究提供了重要参考。算法实现过程清晰,结合图结构构建和GCN特征传播,适合处理非欧几里得数据结构的图像修复任务。
相关文章:

mathematics-2024《Graph Convolutional Network for Image Restoration: A Survey》
推荐深蓝学院的《深度神经网络加速:cuDNN 与 TensorRT》,课程面向就业,细致讲解CUDA运算的理论支撑与实践,学完可以系统化掌握CUDA基础编程知识以及TensorRT实战,并且能够利用GPU开发高性能、高并发的软件系统…...

IDEA怎么汉化idea中文改回英文版
第一步:点击左上角的File,然后选择Setting 第二步:Setting页面选择 Appearance & Behavior,然后展开System Settings,然后选择 Language and Region,进行修改 我操作的是2024年的版本 File->Settings -> Ap…...

Android minSdk从21升级24后SO库异常
问题 minSdk从21调整到24后: java.nio.file.NoSuchFileException: /data/app/~~Z9s2NfuDdclOUwUBLKnk0A/com.rs.unity- Bg31QvFwF4qsCwv2XCqT-w/split_config.arm64_v8a.apkjava.nio.file.NoSuchFileException: /data/app/~~Z9s2NfuDdclOUwUBLKnk0A/com.rs.unity-…...

车道线检测----CLRKDNet
今天的最后一篇 车道线检测系列结束 CLRKDNet:通过知识蒸馏加速车道检测 摘要:道路车道是智能车辆视觉感知系统的重要组成部分,在安全导航中发挥着关键作用。在车道检测任务中,平衡精度与实时性能至关重要,但现有方法…...

从技术视角解构 Solana Meme 币生态
在高吞吐、高并发的 Solana 网络上,一类轻量化、高热度的代币形式正在爆发式增长——Meme Token(迷因代币)。尽管起源于社群文化,但其技术实现并非“玩笑”,而是一整套构建于 Solana Runtime 与 Token Extensions 之上…...

智能接处警系统:以秒级联动响应重塑应急处置效能
随着我国能源、化工、航空等关键行业的快速发展,传统消防管理模式已难以满足高效应急响应的需求。国家能源局、应急管理部、民航总局均出台专项规定,对消防站建设提出更高要求,在此背景下,智能接处警系统正是应对这些挑战的核…...

OpenCV直方图与直方图均衡化
一、图像直方图基础 1. 什么是图像直方图? 图像直方图是图像处理中最基本且重要的统计工具之一,它用图形化的方式表示图像中像素强度的分布情况。对于数字图像,直方图描述了每个可能的像素强度值(0-255)在图像中出现…...

7-15 计算圆周率
π131352!3573!⋯357⋯(2n1)n!⋯ 输入格式: 输入在一行中给出小于1的阈值。 输出格式: 在一行中输出满足阈值条件的近似圆周率,输出到小数点后6位。 输入样例: 0.01输出样例: 3.132157 我的代码 #i…...

Mosaic数据增强技术
Mosaic 数据增强技术是一种在计算机视觉领域广泛应用的数据增强方法。下面是Mosaic 数据增强技术原理的详细介绍 一、原理 Mosaic 数据增强是将多张图像(通常是 4 张)按照一定的规则拼接在一起,形成一张新的图像。在拼接过程中,会…...

GpuGeek 网络加速:破解 AI 开发中的 “最后一公里” 瓶颈
摘要: 网络延迟在AI开发中常被忽视,却严重影响效率。GpuGeek通过技术创新,提供学术资源访问和跨国数据交互的加速服务,助力开发者突破瓶颈。 目录 一、引言:当算力不再稀缺,网络瓶颈如何破局? …...

Sigmoid与Softmax:从二分类到多分类的深度解析
Sigmoid与Softmax:从二分类到多分类的深度解析 联系 函数性质:二者都是非线性函数 ,也都是指数归一化函数,可将输入值映射为0到1之间的实数 ,都能把输出转化成概率分布的形式,在神经网络中常作为激活函数使用。Softmax是Sigmoid的推广:从功能角度看,Softmax函数可视为…...

容器编排利器-k8s入门指南
Kubernetes(K8s)入门指南:容器编排利器 什么是 Kubernetes? Kubernetes(常简称为K8s)是一个开源的容器编排平台,由 Google 开源并交由云原生计算基金会(CNCF)管理。它可以帮助我们自动化部署、扩展和管理容器化应用程序。 为什么需要 Kubernetes? 在微服务架构盛行的今…...
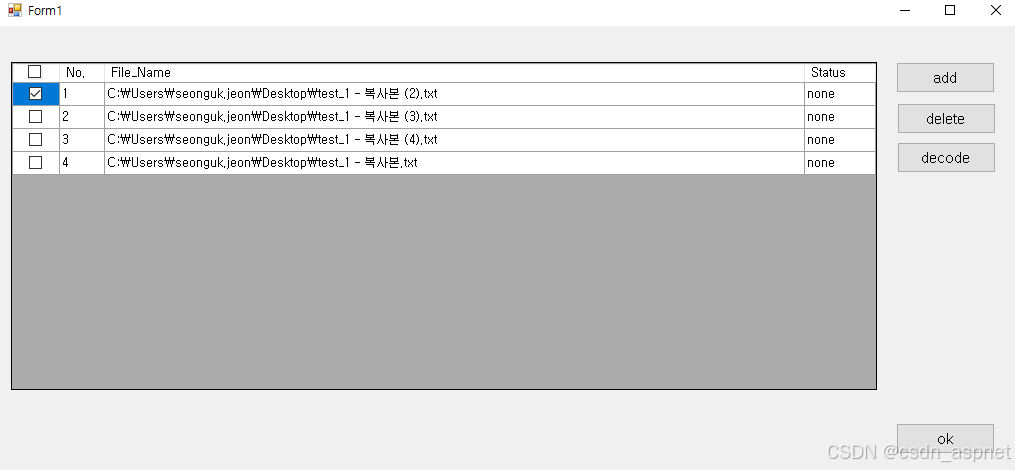
C# DataGridView 选中所有复选框
问题描述 在程序中尝试选中所有复选框,但出现错误。如果单击顶部的完整选中/释放复选框,同时选中包含复选框的列,则选定区域不会改变。该如何解决? 上面的图片是点击完整版本之后的。 下面是本文的测试代码,函数 dat…...

C#学习第23天:面向对象设计模式
什么是设计模式? 定义:设计模式是软件开发中反复出现的特定问题的解决方案。它们提供了问题的抽象描述和解决方案。目的:通过提供成熟的解决方案,设计模式可以加快开发速度并提高代码质量。 常见的设计模式 设计模式通常分为三大…...

LineBasicMaterial
LineBasicMaterial 描述 用于绘制纯色线条的基础材质,支持颜色、线宽和纹理映射。常用于THREE.Line或THREE.LineSegments几何体。 构造函数 (Constructor) 构造函数参数描述LineBasicMaterial(parameters?: Object)parameters定义材质外观的对象,可…...

AB Download Manager v1.5.8 开源免费下载工具
下载文件是我们日常工作和生活中经常进行的操作。面对动辄数十GB的4K影片、设计素材包或开发工具,传统浏览器的单线程下载如同"涓涓细流",非常影响我们的效率和体验。 那么,一款高效且易用的下载工具至关重要。今天就让我们解锁这…...

react-native中createContext的使用
在 React Native 中,createContext 是一个非常强大的工具,用于在组件树中共享状态,避免了逐层传递 props 的繁琐。以下是对 createContext 的详细解释以及一个完整的示例。 详细解释 createContext 是 React 提供的一个函数,用于…...

深度剖析:Dify+Sanic+Vue+ECharts 搭建 Text2SQL 项目 sanic-web 的 Debug 实战
目录 项目背景介绍sanic-web Dify\_service handle\_think\_tag报错NoneType问题描述debug Dify调用不成功,一直转圈圈问题描述debug 前端markdown格式只显示前5页问题描述debug1. 修改代码2.重新构建1.1.3镜像3.更新sanic-web/docker/docker-compose.yaml4. 重新部…...

学习51单片机02
吐血了,板子今天才到,下午才刚开始学的,生气了,害我笔记都断更了一天。。。。 紧接上文...... 如何将HEX程序烧写到程序? Tips:HEX 文件是一种常用于单片机等嵌入式系统的文件格式,它包含了程序的机器码…...
麒麟服务器操作系统安装 MySQL 8 实战指南
往期好文连接:统信UOS/麒麟KYLINOS安装JDBC驱动包 Hello,大家好啊,今天给大家带来一篇麒麟服务器操作系统上安装 MySQL 8 的文章,欢迎大家分享点赞,点个在看和关注吧!MySQL 作为主流开源数据库之一&#x…...
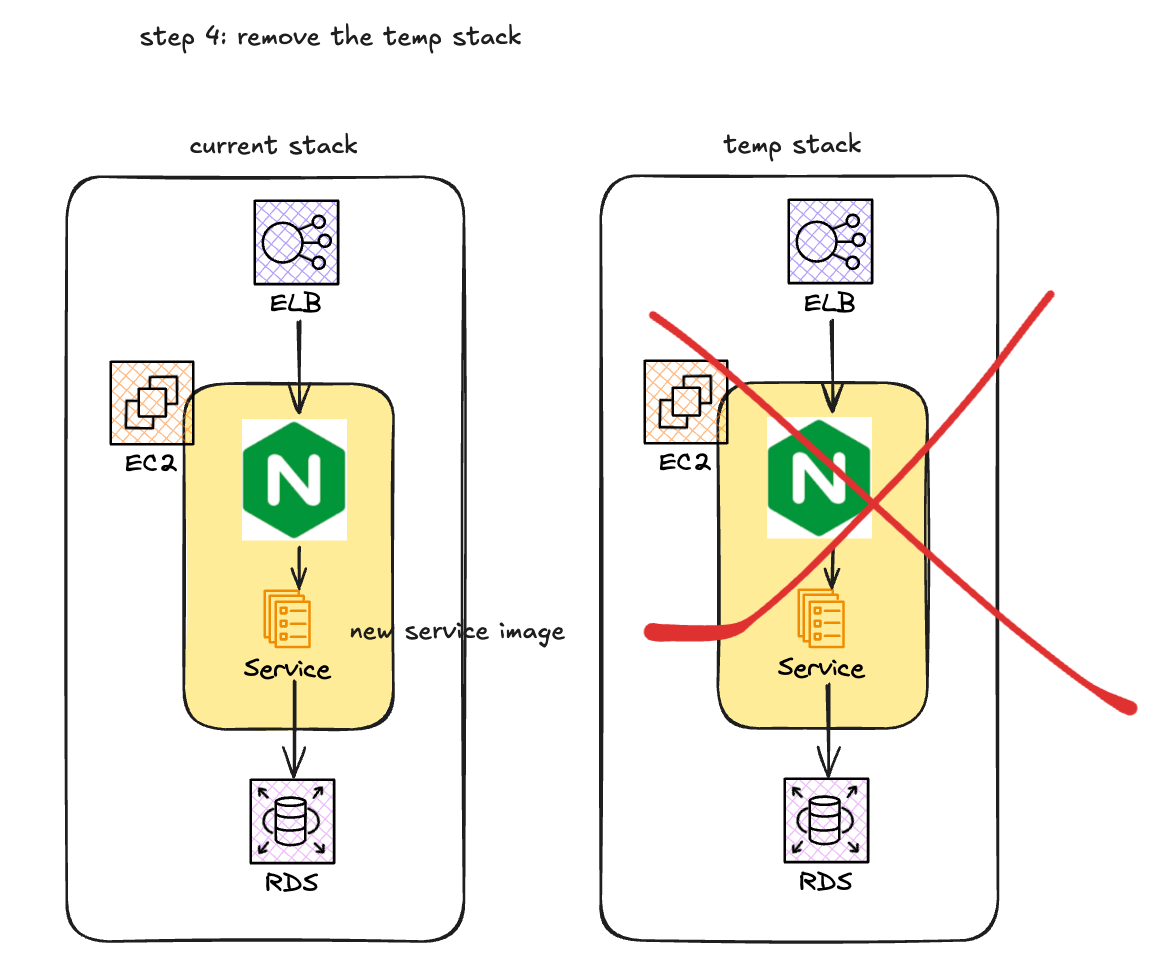
AWS EC2 微服务 金丝雀发布(Canary Release)方案
为什么需要实现金丝雀发布? 在当前项目的工程实践中, 已经有了充分的单元测试, 预发布环境测试, 但是还是会在线上环境出现非预期的情况, 导致线上事故, 因此, 为了提升服务质量, 需要线上能够有一个预验证的机制. 如何实现金丝雀发布? 使用AWS code deploy方案 AWS code…...

力扣-78.子集
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。 解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。 class Solution {List<List<Integer>> res new ArrayList<>();List<I…...

支持蓝牙5.0和2.4G私有协议芯片-PHY6222
PHY6222QC-W04C 是一款适用于蓝牙低功耗(BLE)5.2 应用的片上系统(SoC)。它搭载 ARM Cortex™-M0 32 位处理器,配备 64KB SRAM、512K Flash、96KB ROM、256 bit efuse ,以及超低功耗、高性能的多模式射频模块…...

Jenkins的流水线执行shell脚本执行jar命令后项目未启动未输出日志问题处理
现象 在流水线里配置了启动脚本例如,nohup java -jar xxx.jar >nohup.out 2>&1 & 但是在服务器发现服务并未启动,且nohup日志里没输出日志,这样的原因是jenkins在执行完脚本后,就退出了这个进程。 解决 在启动脚本执行jar命令的上一步…...
 中配置 MCP(Model Context Protocol))
在 Visual Studio Code (VSCode) 中配置 MCP(Model Context Protocol)
前提条件 安装 VSCode:确保已安装最新版本的 VSCode(建议使用 1.99 或以上版本,支持 MCP)。安装 GitHub Copilot 扩展:MCP 通常与 GitHub Copilot 的代理模式(Agent Mode)结合使用,…...

图像锐化调整
一、背景介绍 之前找多尺度做对比度增强时候,发现了一些锐化相关算法,正好本来也要整理锐化,这里就直接顺手对之前做过的锐化大概整理了下,方便后续用的时候直接抓了。 这里整理的锐化主要是两块:一个是参考论文&#…...

我设计的一个安全的 web 系统用户密码管理流程
作为一名有多年经验的前端,在刚开始学习web后端的时候,就对如何设计一个安全的 web 系统用户密码管理流程有很多疑问。之前自己也实践过几种方法,但一直觉得不是十分安全。 我们知道,用户在注册或登录界面填写的密码是明文的&…...

Vue.js---计算属性computed和lazy
4.6 计算属性computed和lazy 懒执行的effect:一般的effect一下子就执行了,但是懒加载effect是等需要的时候才会执行 这时我们通过在options中添加lazy属性来达到目的 function effect (fn , options {}) {const effectFn () > {// 调用clearup函数…...

找客户的app
找客户的 app 在竞争激烈的商业环境中,找客户的 APP 成为企业拓展业务的利器。 微拓客 APP,集智能获客、营销素材、客户管理于一体。支持关键词、附近客源等多方式采集,覆盖 300 行业;一键采集客源,一键导出到通讯录…...

HarmonyOS学习
个人简介 👨💻个人主页: 魔术师 📖学习方向: 主攻前端方向,正逐渐往全栈发展 🚴个人状态: 研发工程师,现效力于政务服务网事业 🇨🇳人生格言&…...
