LeetCode --- 156双周赛
题目列表
3541. 找到频率最高的元音和辅音
3542. 将所有元素变为 0 的最少操作次数
3543. K 条边路径的最大边权和
3544. 子树反转和
一、找到频率最高的元音和辅音

分别统计元音和辅音的出现次数最大值,然后相加即可,代码如下
// C++
class Solution {const string str = "aeiou";
public:int maxFreqSum(string s) {int cnt[26]{};int mx1 = 0, mx2 = 0;for(auto & e : s){cnt[e - 'a']++;if(str.find(e) == string::npos){mx1 = max(mx1, cnt[e - 'a']); // 更新辅音}else{mx2 = max(mx2, cnt[e - 'a']); // 更新辅音}}return mx1 + mx2;}
};
# Python
class Solution:def maxFreqSum(self, s: str) -> int:cnt = [0] * 26mx1 = 0mx2 = 0for e in s:x = ord(e) - ord('a')cnt[x] += 1if e in "aeiou":mx1 = max(mx1, cnt[x])else:mx2 = max(mx2, cnt[x])return mx1 + mx2
二、将所有元素变为 0 的最少操作次数

本题的难点在于一旦我们将区间内的最小值变为 0,那么剩余的不为 0 的数字就会被分成一段一段的区间,此时,我们需要在这些区间内再去进行操作,而这需要我们维护区间内的最小值,显然很困难,那有没有什么其他的思路?
-
思路
对于一个数字x来说,只有当它是区间内的最小值时,才可以通过操作被置为0,而从贪心的角度来说,这个区间越大,则置为0的数越多,所进行的操作就会越少。所以我们只要计算对于同一个数字x,它需要被分为多少个区间,才能让所有的x全部变为0,而它分出的区间数就是它需要进行的最少操作次数。统计所有的数字对于答案的贡献即可- 这里暗含一个贪心的策略,优先将小的数字置为
0会更优,因为小的数字置为0,它依旧是小的数字,不会影响大的数字的分区个数,但是反过来,大的数字置为0,就有可能将小的数字分成更多的区间,导致操作次数变多 - 故这里我们计算出每个数字区间个数后直接相加,看似不论顺序,实质是从小的数字开始进行操作
- 求解
x为最小数字的区间,本质是求距离x最近的比它小的数字下标,可以用单调栈来求解
- 这里暗含一个贪心的策略,优先将小的数字置为
// C++
class Solution {
public:int minOperations(vector<int>& nums) {int n = nums.size();stack<int> st;vector<int> left(n, -1), right(n, n);// 计算区间for(int i = 0; i < n; i++){while(st.size() && nums[st.top()] > nums[i]){right[st.top()] = i;st.pop();}st.push(i);}st = stack<int>();for(int i = n - 1; i >= 0; i--){while(st.size() && nums[st.top()] > nums[i]){left[st.top()] = i;st.pop();}st.push(i);}unordered_map<int,set<pair<int,int>>> mp;for(int i = 0; i < n; i++){mp[nums[i]].emplace(left[i], right[i]);}int ans = 0;for(auto& [x, st] : mp){if(x){ // x = 0 不需要进行操作ans += st.size();}}return ans;}
};
-
优化
- 对于求区间个数的操作,我们可以在一次循环中得到,具体如下
// C++
class Solution {
public:int minOperations(vector<int>& nums) {int n = nums.size(), ans = 0;stack<int> st; // 单调递增 & 栈中无重复数字 & 不包含 0for(int i = 0; i < n; i++){while(st.size() && nums[st.top()] >= nums[i]){// 这里只统计一定需要进行一次操作的数字个数,即左右边界已经明确的数字// 和 nums[i] 相同的数字,由于右边界还不确定,此处不统计,等区间明确后在统计if(nums[st.top()] != nums[i]){ans++;}st.pop();}if(nums[i]) // 0 不需要入栈st.push(i);}// 栈中剩余的数字,此时右边界已经确定,也需要进行一次操作才能被置为 0return ans + st.size();}
};
#Python
class Solution:def minOperations(self, nums: List[int]) -> int:ans = 0bottom, top = 0, 0 # 可以直接将 nums 当作栈进行使用,空间复杂度为 O(1)for i in range(len(nums)):while bottom != top and nums[top-1] >= nums[i]:if nums[top-1] != nums[i]:ans += 1top -= 1if nums[i] > 0:nums[top] = nums[i]top += 1return ans + top - bottom
三、K 条边路径的最大边权和

本题先建图,然后直接用 dfs 进行遍历即可,注意,为了防止重复遍历某个状态,需要记忆化已经遍历过的状态,代码如下
// C++
class Solution {
public:int maxWeight(int n, vector<vector<int>>& edges, int k, int t) {vector<vector<pair<int,int>>> g(n);for(auto& e : edges){g[e[0]].emplace_back(e[1], e[2]);}int ans = -1;set<tuple<int,int,int>> st; // 记忆化遍历过的状态auto dfs = [&](this auto&& dfs, int x, int d, int s)->void{if(d == k){ans = max(ans, s);return;}if(st.count({x, d, s}))return;st.emplace(x, d, s);for(auto& [y, w] : g[x]){if(s + w < t){dfs(y, d + 1, w + s);}}};for(int i = 0; i < n; i++){dfs(i, 0, 0);}return ans;}
};
# Python
class Solution:def maxWeight(self, n: int, edges: List[List[int]], k: int, t: int) -> int:g = [[] for _ in range(n)]for x, y, w in edges:g[x].append((y, w))ans = -1@cachedef dfs(x:int, d:int, s:int):if d == k:nonlocal ansans = max(ans, s)returnfor y, w in g[x]:if w + s < t:dfs(y, d + 1, w + s)for i in range(n):dfs(i, 0, 0)return ans
四、子树反转和

本题的反转操作有距离限制,也就是说对当前结点进行反转操作之后,与它距离小于 k 的结点就不能进行反转操作了,所以我们在 dfs 遍结点的时候,需要增加两个参数 mul : 表示当前的结点取正还是取负,cd : 多少距离后,就能再次进行反转操作,故我们有 dfs(x,fa,mul,cd)
- 当
x结点不反转时, d f s ( x , f a , m u l , c d ) = s u m ( d f s ( y , x , m u l , ( c d ? c d − 1 , 0 ) ) ) + ( m u l ? n u m s [ x ] : − n u m s [ x ] ) dfs(x,fa,mul,cd)=sum(dfs(y,x,mul,(cd\ ?\ cd-1,0)))+(mul\ ?\ nums[x]\ : \ -nums[x]) dfs(x,fa,mul,cd)=sum(dfs(y,x,mul,(cd ? cd−1,0)))+(mul ? nums[x] : −nums[x]),其中y是结点x的所有子节点 - 当
x结点反转且cd == 0时, d f s ( x , f a , m u l , c d ) = s u m ( d f s ( y , x , ! m u l , k − 1 ) ) + ( m u l ? − n u m s [ x ] : n u m s [ x ] ) dfs(x,fa,mul,cd)=sum(dfs(y,x,!mul,k-1))+(mul\ ?\ -nums[x]\ : \ nums[x]) dfs(x,fa,mul,cd)=sum(dfs(y,x,!mul,k−1))+(mul ? −nums[x] : nums[x]),其中y是结点x的所有子节点
代码如下
// C++
class Solution {
public:long long subtreeInversionSum(vector<vector<int>>& edges, vector<int>& nums, int k) {int n = nums.size();vector<vector<int>> g(n);for(auto & e : edges){g[e[0]].push_back(e[1]);g[e[1]].push_back(e[0]);}vector memo(n, vector(2, vector<long long>(k, -1)));auto dfs = [&](this auto&& dfs, int x, int fa, bool mul, int cd)->long long{ // f0, cd0, f1if(memo[x][mul][cd] != -1) return memo[x][mul][cd];long long res = mul ? nums[x] : -nums[x];for(int y : g[x]){if(y != fa){res += dfs(y, x, mul, (cd ? cd - 1 : 0));}}if(cd == 0){long long res2 = mul ? -nums[x] : nums[x];for(int y : g[x]){if(y != fa){res2 += dfs(y, x, !mul, k - 1);}}res = max(res, res2);}return memo[x][mul][cd] = res;};return dfs(0, -1, true, 0);}
};
# Python
class Solution:def subtreeInversionSum(self, edges: List[List[int]], nums: List[int], k: int) -> int:n = len(nums)g = [[] for _ in range(n)]for x,y in edges:g[x].append(y)g[y].append(x)memo = {}def dfs(x:int, fa:int, mul:bool, cd:int)->int:t = (x, mul, cd)if t in memo:return memo[t]res = nums[x] if mul else -nums[x]for y in g[x]:if y != fa:res += dfs(y, x, mul, cd - 1 if cd > 0 else 0)if cd == 0:res2 = -nums[x] if mul else nums[x]for y in g[x]:if y != fa:res2 += dfs(y, x, not mul, k - 1)res = max(res, res2)memo[t] = resreturn resreturn dfs(0, -1, True, 0)
相关文章:

LeetCode --- 156双周赛
题目列表 3541. 找到频率最高的元音和辅音 3542. 将所有元素变为 0 的最少操作次数 3543. K 条边路径的最大边权和 3544. 子树反转和 一、找到频率最高的元音和辅音 分别统计元音和辅音的出现次数最大值,然后相加即可,代码如下 // C class Solution {…...

模型量化AWQ和GPTQ哪种效果好?
环境: AWQ GPTQ 问题描述: 模型量化AWQ和GPTQ哪种效果好? 解决方案: 关于AWQ(Adaptive Weight Quantization)和GPTQ(Generative Pre-trained Transformer Quantization)这两种量化方法的…...

npm 报错 gyp verb `which` failed Error: not found: python2 解决方案
一、背景 npm 安装依赖报如下错: gyp verb check python checking for Python executable "python2" in the PATH gyp verb which failed Error: not found: python2 一眼看过去都觉得是Python环境问题,其实并不是你python环境问题…...

初识Linux · IP协议· 下
目录 前言: 内网IP和公网IP 内网IP 公网IP 路由 前言: 前文我们介绍了IP协议的协议头,通过源码等方式我们理解了IP协议中的字段,比如8位协议,比如通过环回问题引出的8位最大生存时间,比如8位协议&…...

5.27本日总结
一、英语 复习list2list29 二、数学 学习14讲部分内容 三、408 学习计组1.2内容 四、总结 高数和计网明天结束当前章节,计网内容学完之后主要学习计组和操作系统 五、明日计划 英语:复习lsit3list28,完成07年第二篇阅读 数学&#…...

JavaScript基础-创建对象的三种方式
在JavaScript中,对象是构建复杂数据结构和实现面向对象编程的核心。掌握如何创建对象对于每个开发者来说都是必不可少的技能。本文将介绍创建JavaScript对象的三种主要方式:对象字面量、构造函数以及类(ES6引入),并探讨…...

JAVA的常见API文档(上)
游戏打包 注意API文档中的方法不需要记忆!! 了解之后如果需要可以查询API文档 对Math的方法总结: 运用刚学的Math方法加快代码的运行效率 可以减少循环次数 找规律: 发现因子有规律: 必定一个大于平方根,…...

JavaScript 中的 for...in 和 for...of 循环详解
在 JavaScript 中,for...in 和 for...of 是两种常用的循环结构,但它们有着不同的用途和行为。很多初学者容易混淆这两者,本文将详细解析它们的区别、适用场景以及注意事项。 目录 for…in 循环 基本用法遍历对象属性注意事项 for…of 循环 …...

AtCoder AT_abc406_c [ABC406C] ~
前言 除了 A 题,唯一一道一遍过的题。 题目大意 我们定义满足以下所有条件的一个长度为 N N N 的序列 A ( A 1 , A 2 , … , A N ) A(A_1,A_2,\dots,A_N) A(A1,A2,…,AN) 为波浪序列: N ≥ 4 N\ge4 N≥4(其实满足后面就必须满足这…...

Spark,连接MySQL数据库,添加数据,读取数据
连接数据库 可以看到shell中我们读取出的数据 在IDEA中打代码如果能输出跟shell中一样的结果即证明连接成功 【出错反思】 像我前面出错的原因就是在打代码时将密码输入错误 添加数据 读取数据就是在上面代码中一起展示了,这里我就不单独说了...

Linux容器技术详解
容器技术基础 什么是容器 容器是一种轻量级的虚拟化技术,它将应用程序及其依赖(库、二进制文件、配置文件等)打包在一个独立的单元中,可以在任何支持容器运行时的环境中一致地运行。 Docker官网:https://www.docker…...

【EDA软件】【联合Modelsim仿真使用方法】
背景 业界EDA工具仿真功能是必备的,例如Vivado自带仿真工具,且无需联合外部仿真工具,例如MoodelSim。 FUXI工具仿真功能需要联合Modelsim,才能实现仿真功能。 方法一:FUXI联合ModelSim 1 添加testbench文件 新建to…...

STM32 __main
STM32开发中__main与用户main()函数的本质区别及工作机制 在STM32开发中,__main和用户定义的main()函数是启动过程中的两个关键节点,分别承担运行时初始化和用户程序入口的职责。以下是它们的核心差异及协作机制: 一、定义与层级差异 __ma…...

【离散化 线段树】P3740 [HAOI2014] 贴海报|普及+
本文涉及知识点 C线段树 [HAOI2014] 贴海报 题目描述 Bytetown 城市要进行市长竞选,所有的选民可以畅所欲言地对竞选市长的候选人发表言论。为了统一管理,城市委员会为选民准备了一个张贴海报的 electoral 墙。 张贴规则如下: electoral…...

Python训练营打卡Day28
浙大疏锦行 DAY 28 类的定义和方法 知识点回顾: 1.类的定义 2.pass占位语句 3.类的初始化方法 4.类的普通方法 5.类的继承:属性的继承、方法的继承 作业 题目1:定义圆(Circle)类 要求: 1.包含属性&#x…...

MODBUS RTU通信协议详解与调试指南
一、MODBUS RTU简介 MODBUS RTU(Remote Terminal Unit)是一种基于串行通信(RS-485/RS-232)的工业标准协议,采用二进制数据格式,具有高效、可靠的特点,广泛应用于PLC、传感器、变频器等工业设备…...

CSP 2024 提高级第一轮(CSP-S 2024)单选题解析
单选题解析 第 1 题 在 Linux 系统中,如果你想显示当前工作目录的路径,应该使用哪个命令?(A) A. pwd B. cd C. ls D. echo 解析:Linux 系统中,pwd命令可以显示当前工作目录的路径。pwd&#x…...

六、绘制图片
文章目录 1.创建一个红色图片2.加载bmp图片3.加载png、jpg图片 前面的几个示例,我们已经展示过如果在Linux系统下使用xlib接口向窗口中绘制文本、线、矩形;并设置文本、线条的颜色。并利用xlib提供的接口结合事件处理机制完成了一个自绘按钮控件功能。有…...

Java 面向对象详解和JVM底层内存分析
先关注、点赞再看、人生灿烂!!!(谢谢) 神速熟悉面向对象 表格结构和类结构 我们在现实生活中,思考问题、发现问题、处理问题,往往都会用“表格”作为工具。实际上,“表格思维”就是…...

深度学习---知识蒸馏(Knowledge Distillation, KD)
一、知识蒸馏的本质与起源 定义: 知识蒸馏是一种模型压缩与迁移技术,通过将复杂高性能的教师模型(Teacher Model)所学的“知识”迁移到轻量级的学生模型(Student Model),使学生模型在参数量和计…...

基于CNN卷积神经网络的带频偏QPSK调制信号检测识别算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 (完整程序运行后无水印) 2.算法运行软件版本 matlab2024b 3.部分核心程序 (完整版代码包含详细中文注释和操作步骤视频)…...
【DAY21】 常见的降维算法
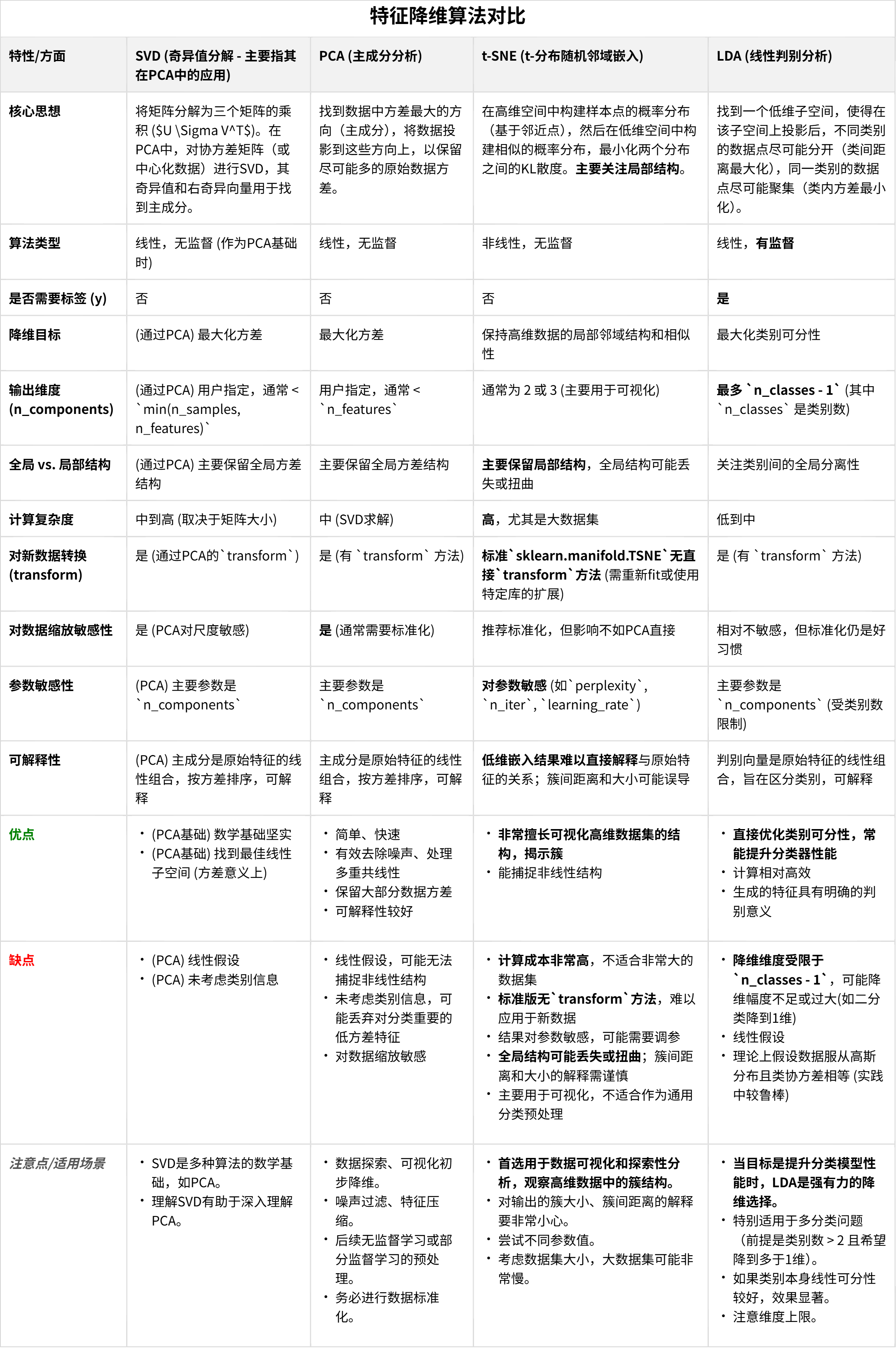
内容来自浙大疏锦行python打卡训练营 浙大疏锦行 目录 PCA主成分分析 t-sne降维 线性判别分析 (Linear Discriminant Analysis, LDA) 作业: 什么时候用到降维 降维的主要应用场景 知识点回顾: PCA主成分分析t-sne降维LDA线性判别 通常情况下,…...

PostGIS实现栅格数据入库-raster2pgsql
raster2pgsql使用与最佳实践 一、工具概述 raster2pgsql是PostGIS提供的命令行工具,用于将GDAL支持的栅格格式(如GeoTIFF、JPEG、PNG等)导入PostgreSQL数据库,支持批量加载、分块切片、创建空间索引及金字塔概览,是栅格数据入库的核心工具。 二、核心功能与典型用法 1…...

校园社区小程序源码解析
基于ThinkPHP、FastAdmin和UniApp开发的校园社区小程序源码,旨在为校园内的学生和教职员工提供一个便捷的在线交流和服务平台。 该小程序前端采用UniApp进行开发,具有良好的跨平台兼容性,可以轻松发布到iOS和Android平台。同时,后…...

第6章:文件权限
一、文件权限概述 Linux为了保证系统中每个文件的安全,引入了文件权限机制。针对于系统中的每一个文件Linux都可以提供精确的权限控制。它可以做到不同的用户对同一个文件具有不同的操作权利。而通常这个权利包括以下3个: 读的权利(Read&…...

使用 Python 连接 Oracle 23ai 数据库完整指南
方法一:使用 oracledb 官方驱动(推荐) Oracle 官方维护的 oracledb 驱动(原 cx_Oracle)是最新推荐方案,支持 Thin/Thick 两种模式。 1. 环境准备 pip install oracledb2. 完整示例代码 import oracledb import getpass from typing import Unionclass Oracle23aiConn…...

C语言| 指针变量的定义
C语言| 指针的优点-CSDN博客 * 表示“指向”,为了说明指针变量和它所指向的变量之间的联系。 int * i;//表示指针变量i里面存放的地址,所指向的存储单元里的【数据】。 【指针变量的定义】 C语言规定所有变量,在使用前必须先定…...

HTML 中的 input 标签详解
HTML 中的 input 标签详解 一、基础概念 1. 定义与作用 HTML 中的 <input> 标签是表单元素的核心组件,用于创建各种用户输入字段。作为一个空标签(没有闭合标签),它通过 type 属性来决定呈现何种输入控件,是实…...

Python 在自动驾驶数据标签中的应用:如何让 AI 读懂道路?
Python 在自动驾驶数据标签中的应用:如何让 AI 读懂道路? 在自动驾驶系统中,数据就是生命线。不管是摄像头、激光雷达还是雷达传感器,这些设备每天都能产生 海量数据,但如果这些数据没有被正确标注,它们对 AI 来说毫无意义。那么,如何让自动驾驶系统准确理解道路环境呢…...

微信小程序之按钮短时间内被多次点击问题
做项目的时候碰到这个问题,按钮的功能做好了,但是总会出现按的太快,出现不可预料的问题。 解决方法之一:借助函数节流来实现 1、创建一个工具包(throttle.js),通过封装一个高阶函数,对函数的执…...
