BBR 的 buffer 动力学观感
这周很忙,今天还加了一天班,但还是抽空实现了五一在安徽泾县山区喝着一壶酒写的 BBR ProbeRTT 的想法,没多少行代码,它真就消除了带宽锯齿,皮了个鞋👞,昨天我还在群里说了今天再说说 BBR 的,回到家就作图作文了。
去年夏天,我花了些精力量化 BBR 动力学,并给出一些相图以及收敛方程的数值解,但数学也只是描述而非解释,就像牛顿定律只能描述万有引力却无法解释引力的由来(任何理论都无法解释)一样。所以这个话题要不断推敲,常看常新,搞不好就有新思路了。
BBR 动力学核心是收敛,归为一句话就是 “带宽越大 Probe 加速比越小”,这句话是收敛的原因,进一步通俗解释,大的想更大更难,是为边际收益递减,小的想更大也难,但边际收益单调递减,却仍高于大的,相对而言其加速比就更大。buffer 动力学解释,即小流 Probe 的结果比大流的更大,大流就表现出净损而让给小流了。
《道德经》里早有论述,“天之道,损有余而补不足”,看来这是天道,容不得解释。而 “人之道则不然,损不足以奉有余”,则与《新约 · 马太福音》相呼应了。
我也常常提到 “矩”,它是一个乘积,与一个值不同的是,它体现了两个维度的胶合,两个维度的矩针对一个维度的值,其结果就是边际收益递减了,因为两个维度的伸缩比例并不常一致,所谓矩的效应,就比如面积相同而周长不等,或周长相同而面积各异,正如力和力臂,矩不变,但费料不同。
套用解释 buffer 动力学,BDP 就是挤出带宽的矩,BBR 靠 1.25 倍增益来体现边际收益递减,直到当它继续再减下去时,对方也要跟着减下去,这时候收敛到公平,方可停止,惊奇的是,这件事确实自然发生。
5 月 2 日晚,我在安徽宣城写了一篇 BBR ProbeRTT 新改,提出一个新思路,近日测试,是那么回事。我大致说的是,BBR 一定需要借宿于 buffer 中收敛到公平,为守其初衷,却又要 ProbeRTT,但原生 ProbeRTT 的假设太苛刻,对全局同步过度依赖,这境况在强弱不等的持续统计波动中未必能保持,何不哺其糟而歠其醨,将自己因 Probe 而建立的 queue 吐出即可。
我模仿 Jaffe’s style,用四则混合运算描述 BBR buffer 动力学,基于表达式推出一个结论,基于该结论给出上述 ProbeRTT 描述,即刻取消 BBR 由于 ProbeRTT 导致的邪恶带宽锯齿(BBR 终于摆脱了 cwnd 锯齿,却为何还要面对 bw 锯齿)。
设总带宽为 1,流 1 带宽为 x,则流 2 带宽则为 1 - x,以 ProbeBW 之 ProbeUP phase 论,流 1 和流 1 的带宽增量表示为:
f 1 ( x ) = g ⋅ x g ⋅ x + 1 − x − x x + 1 − x f_1(x)=\dfrac{\mathrm{g}\cdot x}{\mathrm{g}\cdot x+1-x}-\dfrac{x}{x+1-x} f1(x)=g⋅x+1−xg⋅x−x+1−xx
f 2 ( x ) = g ⋅ ( 1 − x ) g ⋅ ( 1 − x ) + x − ( 1 − x ) ( 1 − x ) + x f_2(x)=\dfrac{\mathrm{g}\cdot (1-x)}{\mathrm{g}\cdot (1-x)+x}-\dfrac{(1-x)}{(1-x)+x} f2(x)=g⋅(1−x)+xg⋅(1−x)−(1−x)+x(1−x)
不必化简,直接画图:

最下面灰线是 f1(x) - f2(x),可清晰看出 x = 0.5 的分水岭,当 x < 0.5,f1(x) 属小流带宽演进,f2(x) 属大流带宽演进,小流挤压大流带宽,反之亦然。
这也不难直观理解,以 AIMD 为例,当 x,y 分别为两流不同的初始 cwnd 时,设 x < y,那么 x + L y + L \dfrac{x+L}{y+L} y+Lx+L 当 L 越大,值越趋向 1 收敛到公平,即只要 additive increase 一直持续,总会收敛,BBR 同样,每次 Probe 都会堆一小丢丢 queue,大流堆的少,小流堆得更多些, x + L b i g g e r y + L s m a l l e r \dfrac{x+L_{bigger}}{y+L_{smaller}} y+Lsmallerx+Lbigger 看起来要比 AIMD 更快趋向 1,但 L 都超级小(如图所示,我还特意缩放了坐标比例),总体上还是 AIMD 应有的收敛速度。
f1(x),f2(x) 显然关于 x = 0.5 对称,它们之做差结果显示了 “损有余而补不足” 的过程,该过程强度逐渐收缓(如图绿蓝线之间的间隙),直至两者再无差异,它们与 x = 0.5 相交的此点即稳定点,它是不动点。
依照上述 5 月 2 日的 ProbeRTT 方法,释放自己堆积的 queue,在上图的意义就是分别求绿线 x 到 0.5 以及蓝线 0.5 到 1 - x 的积分,肉眼观测,面积是相等的,大差不差一个相位。
现在演示一下实际上是不是这样:
import numpy as np
import matplotlib.pyplot as plt
import randomx0 = 0.2
y0 = 0.8
g = 1.25
bx, by = 0, 0
R = 2
C = 1num_steps = 500
t = np.arange(num_steps) # 带宽
x = np.zeros(num_steps)
y = np.zeros(num_steps)
# BDP
Bx = np.zeros(num_steps)
By = np.zeros(num_steps)
# RTwait
r = np.zeros(num_steps)
# 自己堆占的 queue
Ax = np.zeros(num_steps)
Ay = np.zeros(num_steps)
# 自己堆栈 queue 的平均
sAx = np.zeros(num_steps)
sAy = np.zeros(num_steps)x[0] = x0
y[0] = y0
r[0] = 0Bx[0], By[0] = x0, y0
Ax[0], Ay[0], sAx[0], sAy[0] = 0, 0, 0, 0
nx, ny = random.randint(5, 15), random.randint(5, 15)for i in range(1, num_steps):if i > 150:C = 5if i > 350:C = 0.2dec = 0x[i] = C * (g * x[i-1]) / (g * x[i-1] + y[i-1]) tx = C * x[i-1] / (x[i-1] + y[i-1])bx += R * (x[i] - tx)if i % nx == 0: # x 随意 ProbeRTT,不再依赖同步dec += bxbx = 0 # 退掉自己 Probe 造成的 queue,堆多少退多少nx = random.randint(5, 15)Ax[i] = bxsAx[i] = 0.9 * sAx[i-1] + 0.1 * bx#y[i-1] = C - x[i] # 忘记 max-filter bwy[i] = C * (g * y[i-1]) / (g * y[i-1] + x[i]) ty = C * y[i-1]/(y[i-1] + x[i])by += R * (y[i] - ty)if i % ny == 0: # y 随意 ProbeRTT,不再依赖同步dec += byby = 0 # 退掉自己 Probe 造成的 queue,堆多少退多少ny = random.randint(5, 15)Ay[i] = bysAy[i] = 0.9 * sAy[i-1] + 0.1 * by#x[i] = C - y[i] # 忘记 max-filter bwr[i] = (((x[i] + y[i]) * R) + bx + by- dec) / C - Rif r[i] < 0:r[i] = 0Bx[i] = r[i] * x[i]By[i] = r[i] * y[i]fig, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(8, 6))ax1.plot(t, r, label='rtt(t)', color='green')ax1.plot(t, x, label='bw_x(t)', linestyle=':', color='blue')
ax1.plot(t, y, label='bw_y(t)', linestyle=':', color='red')
ax2.plot(t, Bx, label='bdp_x(t)', linestyle=':')
ax2.plot(t, By, label='bdp_y(t)', linestyle=':')
ax3.plot(t, Ax, label='buf_x(t)', linestyle=':')
ax3.plot(t, Ay, label='buf_y(t)', linestyle=':')
ax3.plot(t, sAx, label='avg_buf_x(t)', linestyle='-')
ax3.plot(t, sAy, label='avg_buf_y(t)', linestyle='-')
ax1.set_xlabel('t')
ax1.set_ylabel('v')
ax2.set_xlabel('t')
ax2.set_ylabel('BDP')
ax2.set_xlabel('t')
ax2.set_ylabel('total buffer')
ax1.legend()
ax1.grid(True)
ax2.legend()
ax2.grid(True)
ax3.legend()
ax3.grid(True)
plt.show()
给出几个结局:

观测到的现象是:
- total buffer 写错了,应该去掉,因为已经有了图例;
- RTT 总体在一个很小范围内波动,视 ProbeRTT 平均期望窗口而定,窗口越大,RTT 振幅越大;
- bw,BDP,自己堆积 queue 总体都属于统计公平状态;
- BDP 随总带宽 C 而涨跌,但整体非常公平;
这才像个真实的样子,没有任何假设和约束,但却收敛到了公平。
但这里有个 BBR 细节,“为什么要在一个 max-filter bw 窗口内至少进入 Probe phase 一次”,比如 10-round 的 max-filter bw 窗口,要设计 8-round 的 ProbeBW cycle。如果将上述 python 代码的两行 “忘记 max-filter bw” 注释放开,结局如下:

这个结果写出递推式就能看明白,完全不必分析不动点和相图。
最后,给出完全由 buffer 动力学驱动而不是照着 “算法” 临摹的实际效果。还是先给出仿真代码:
for i in range(1, num_steps):if i > 150:C = 5if i > 350:C = 0.2dec = 0# 根据 buffer 占比求带宽x[i] = C * (g * x[i-1] * R) / (g * x[i-1] * R + y[i-1] * (r[i-1] + R)) # 如果不 probe 的带宽tx = C * x[i-1] * (r[i-1] + R) / (x[i-1] * (r[i-1] + R) + y[i-1] * (r[i-1] + R))bx += R * (x[i] - tx)# 随机而生的 ProbeRTT,不依赖同步if i % nx == 0:dec += bxbx = 0nx = random.randint(5, 15)# 即时 bufferAx[i] = bx# 即时 buffer 移动指数平均sAx[i] = 0.9 * sAx[i-1] + 0.1 * bx# 同 x,略y[i] = C * (g * y[i-1] * R) / (g * y[i-1] * R + x[i] * (r[i-1] + R)) ty = C * y[i-1] * (r[i-1] + R)/(y[i-1] * (r[i-1] + R) + x[i] * (r[i-1] + R))by += R * (y[i] - ty)if i % ny == 0:dec += byby = 0ny = random.randint(5, 15)Ay[i] = bysAy[i] = 0.9 * sAy[i-1] + 0.1 * by# RTwait = total_bdp / C - RTpropr[i] = (((x[i] + y[i]) * R) + bx + by- dec) / C - Rif r[i] < 0:r[i] = 0Bx[i] = r[i] * x[i]By[i] = r[i] * y[i]
以下几个例子的实际采样结局:

真正的统计律主导,不以精确而以统计应对时局,可以看出 queue 以一个非常有限的振幅波动,没有完全消除,但也不过度增加,且 ProbeRTT 也不再需同步,任意时刻执行均可(在一个最大窗口比如 5~10s 的约束内),它完全通过 buffer 动力学驱动。整体而言,这达到了一个松散的统计公平。
浙江温州皮鞋湿,下雨进水不会胖。
相关文章:

BBR 的 buffer 动力学观感
这周很忙,今天还加了一天班,但还是抽空实现了五一在安徽泾县山区喝着一壶酒写的 BBR ProbeRTT 的想法,没多少行代码,它真就消除了带宽锯齿,皮了个鞋👞,昨天我还在群里说了今天再说说 BBR 的&…...
Spring之Bean的初始化 Bean的生命周期 全站式解析
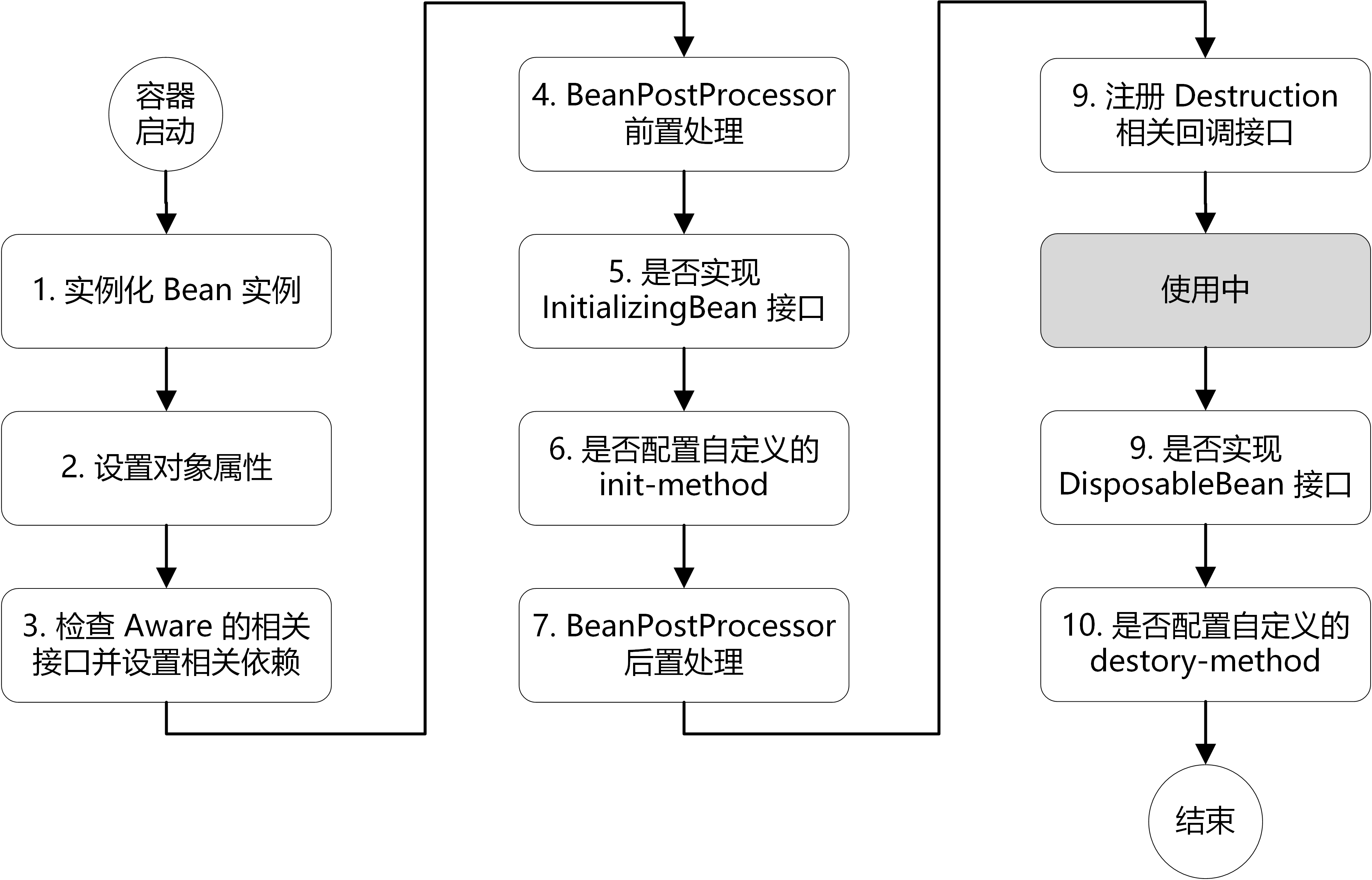
目录 导图 步骤 第一步 实例化 第二步 属性赋值 第三步 初始化 aware 接口 BeanPostProcessor 接口 InitializingBean 和 init-method 第四步使用 第五步使用后销毁 描述一下 Bean 的 生命周期 导图 步骤 总体上可以分为五步 首先是 Bean 的实例化Bean 在进行实例…...
FreeCAD源码分析: Transaction实现原理
本文阐述FreeCAD中Transaction的实现原理。 注1:限于研究水平,分析难免不当,欢迎批评指正。 注2:文章内容会不定期更新。 一、概念 Ref. from What is a Transaction? A transaction is a group of operations that have the f…...
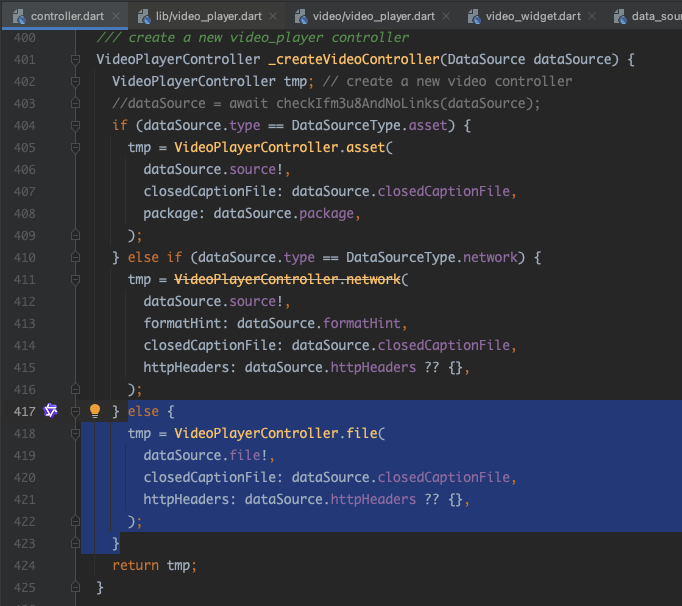
flutter缓存网络视频到本地,可离线观看
记录一下解决问题的过程,希望自己以后可以参考看看,解决更多的问题。 需求:flutter 缓存网络视频文件,可离线观看。 解决: 1,flutter APP视频播放组件调整; 2,找到视频播放组件&a…...

Kotlin 中 infix 关键字的原理和使用场景
在 Kotlin 中,使用 infix 关键字修饰的函数称为中缀函数,使用是可以省略 . 和 (),允许以更自然(类似自然语言)的语法调用函数,这种特性可以使代码更具可读性。 1 infix 的原理 中缀函数必须满足以下条件&…...

c++从入门到精通(五)--异常处理,命名空间,多继承与虚继承
异常处理 栈展开过程: 栈展开过程沿着嵌套函数的调用链不断查找,直到找到了与异常匹配的catch子句为止;也可能一直没找到匹配的catch,则退出主函数后查找过程终止。栈展开过程中的对象被自动销毁。 在栈展开的过程中,…...
)
mock 数据( json-server )
json-server 实现数据 mock 实现步骤: 1. 在项目中安装 json-server npm install -D json-server 2. 准备一个 json 文件 server/data.json {"posts": [{ "id": "1", "title": "a title", "views"…...

Java多线程编程中的常见问题与陷阱汇总
线程安全问题 多线程环境下,多个线程同时访问共享资源时,可能会导致数据不一致或程序行为异常。常见的线程安全问题包括竞态条件、死锁、活锁等。 public class Counter {private int count 0;public void increment() {count;}public int getCount()…...

ARP Detection MAC-Address Static
一、ARP Detection(ARP检测) ✅ 定义: ARP检测是一种防止ARP欺骗攻击的安全机制。它通过监控或验证网络中的ARP报文,来判断是否存在伪造的ARP信息。 🔍 工作原理: 网络设备(如交换机…...

gcc/g++常用参数
1.介绍 gcc用于编译c语言,g用于编译c 源代码生成可执行文件过程,预处理-编译-汇编-链接。https://zhuanlan.zhihu.com/p/476697014 2.常用参数说明 2.1编译过程控制 参数作用-oOutput,指定输出名字-cCompile,编译源文件生成对…...

nginx配置之负载均衡
版权声明:原创作品,请勿转载! 1.实验环境准备 准备3台linux服务器(ubuntu和centos均可,本文使用centos7.9),两台web和一台负载均衡服务器,均安装nginx服务 主机名IP软件lb0110.0.0…...

相机Camera日志分析之十一:高通相机Camx hal预览1帧logcat日志process_capture_result详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:高通相机Camx 日志分析之五:camx hal预览1帧logcat日志process_capture_request详解 这一篇我们开始讲: 高通相机Camx 日志分析之十一:camx hal预览1帧logcat日志process_capture_result详解,这里我…...

Python函数库调用实战:以数据分析为例
一、引言 Python之所以在编程领域广受欢迎,很大程度上得益于其丰富且强大的函数库。这些函数库涵盖了从数据分析、科学计算到Web开发、机器学习等众多领域,极大地提高了开发效率。本文将以数据分析为例,介绍如何调用Python的一些常用函数库。…...

去年开发一款鸿蒙Next Os的window工具箱
持拖载多个鸿蒙应用 批量签名安装 运行 http://dl.lozn.top/lozn/HarmonySignAndFileManagerTool_2024-11-26.zip 同类型安卓工具箱以及其他软件下载地址汇总 http://dl.lozn.top/lozn/ 怎么个玩法呢,比如要启动某app, 拖载识别到包名 点启动他能主动读取包名 然后…...

顶层设计-IM系统架构
一、系统总体架构概览 即时通讯(IM)系统的核心目标,是让用户可以随时随地稳定地发送和接收消息。为了支撑成千上万用户同时在线交流,我们需要将整个系统划分成多个专职模块,每个模块只负责一件事情,彼此协同…...

信任的进阶:LEI与vLEI协同推进跨境支付体系变革
在全球经济版图加速重构的背景下,跨境支付体系正经历着前所未有的变革。2022年全球跨境支付规模突破150万亿美元,但平均交易成本仍高达6.04%,支付延迟超过2.7天。 这种低效率背后,隐藏着复杂的身份识别困境:超过40%的…...
:信息安全的五要素及其含义)
安全性(三):信息安全的五要素及其含义
五要素及其含义 序号要素英文缩写含义说明1保密性Confidentiality仅授权用户才能访问信息,防止信息被非法获取或泄露(例如:加密、访问控制)2完整性Integrity信息在传输、存储和处理过程中保持准确、完整、未被篡改(例…...
)
PHP 与 面向对象编程(OOP)
PHP 是一种支持面向对象编程(OOP)的多范式语言,但其面向对象特性是逐步演进而非原生设计。以下是关键分析: 1. PHP 对面向对象编程的支持 核心 OOP 特性: 类和对象: PHP 支持通过 class 关键字定义类&…...

Axios全解析:从基础到高级实战技巧
目录 核心特性 安装配置 基础使用 高级功能 错误处理 拦截器机制 请求取消 TypeScript支持 最佳实践 常见问题 1. 核心特性 1.1 核心优势 全平台支持:浏览器 & Node.js 双环境 自动转换:JSON数据自动序列化 拦截器系统:请求…...

EXO 可以将 Mac M4 和 Mac Air 连接起来,并通过 Ollama 运行 DeepSeek 模型
EXO 可以将 Mac M4 和 Mac Air 连接起来,并通过 Ollama 运行 DeepSeek 模型。以下是具体实现方法: 1. EXO 的分布式计算能力 EXO 是一个支持 分布式 AI 计算 的开源框架,能够将多台 Mac 设备(如 M4 和 Mac Air)组合成…...

数据库故障排查指南
数据库连接问题 检查数据库服务是否正常运行,确认网络连接是否畅通,验证数据库配置文件的正确性,确保用户名和密码无误。 性能问题 分析慢查询日志,优化SQL语句,检查索引使用情况,调整数据库参数配置&am…...

RBTree的模拟实现
1:红黑树的概念 红⿊树是⼀棵⼆叉搜索树,他的每个结点增加⼀个存储位来表⽰结点的颜⾊,可以是红⾊或者⿊⾊。通过对任何⼀条从根到叶⼦的路径上各个结点的颜⾊进⾏约束,红⿊树确保没有⼀条路径会⽐其他路径⻓出2倍,因…...

docker-compose——安装mongo
编写docker-compose.yml version : 3.8services:zaomeng-mongodb:container_name: zaomeng-mongodbimage: mongo:latestrestart: alwaysports:- 27017:27017environment:- MONGO_INITDB_ROOT_USERNAMEroot- MONGO_INITDB_ROOT_PASSWORDpssw0rdvolumes:- ./mongodb/data:/data/…...

Vue 3.0中响应式依赖和更新
响应式依赖和更新是Vue 3.0中最重要的机制,其核心代码如下,本文将结合代码对这个设计机制作出一些解释。 // 全局依赖存储:WeakMap<target, Map<key, Set<effect>>> const targetMap new WeakMap();// 当前活动的副作用函…...

uniapp|实现获取手机摄像头权限,调用相机拍照实现人脸识别相似度对比,拍照保存至相册,多端兼容(APP/微信小程序)
基于uniapp以及微信小程序实现移动端人脸识别相似度对比,实现摄像头、相册权限获取、相机模块交互、第三方识别集成等功能,附完整代码。 目录 核心功能实现流程摄像头与相册权限申请权限拒绝后的引导策略摄像头调用拍照事件处理人脸识别集成图片预处理(Base64编码/压缩)调用…...

JavaScript【7】BOM模型
1.概述: BOM(Browser Object Model,浏览器对象模型)是 JavaScript 中的一个重要概念,它提供了一系列对象来访问和操作浏览器的功能和信息。与 DOM(Document Object Model)主要关注文档结构不同&…...

[强化学习的数学原理—赵世钰老师]学习笔记02-贝尔曼方程
本人为强化学习小白,为了在后续科研的过程中能够较好的结合强化学习来做相关研究,特意买了西湖大学赵世钰老师撰写的《强化学习数学原理》中文版这本书,并结合赵老师的讲解视频来学习和更深刻的理解强化学习相关概念,知识和算法技…...

使用Spring Boot与Spring Security构建安全的RESTful API
使用Spring Boot与Spring Security构建安全的RESTful API 引言 在现代Web应用开发中,安全性是不可忽视的重要环节。Spring Boot和Spring Security作为Java生态中的主流框架,为开发者提供了强大的工具来构建安全的RESTful API。本文将详细介绍如何结合S…...

深入理解构造函数,析构函数
目录 1.引言 2.构造函数 1.概念 2.特性 3.析构函数 1.概念 2.特性 1.引言 如果一个类中什么都没有,叫作空类. class A {}; 那么我们这个类中真的是什么都没有吗?其实不是,如果我们类当中上面都不写.编译器会生成6个默认的成员函数。 默认成员函数:用户没有显…...

Day 16
目录 1.JZ79 判断是不是平衡二叉树1.1 解析1.2 代码 2.DP10 最大子矩阵2.1 解析2.2 代码 1.JZ79 判断是不是平衡二叉树 JZ79 判断是不是平衡二叉树 dfs 1.1 解析 1.2 代码 /*** struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* TreeNode(in…...
