matlab多智能体网络一致性研究
一个基于连续时间多智能体系统(Multi-Agent Systems, MAS)的一阶一致性协议的MATLAB仿真代码,包含网络拓扑建模、一致性协议设计和收敛性分析。代码支持固定拓扑和时变拓扑,适用于学术研究。
1. 基础模型与代码框架
(1) 网络拓扑建模(图论)
假设有 (N) 个智能体,通过无向图 (G = (V, E)) 连接,邻接矩阵为 (A),度矩阵为 (D),拉普拉斯矩阵 (L = D - A)。
% 生成一个包含5个节点的环形拓扑
N = 5;
A = zeros(N, N);
for i = 1:NA(i, mod(i, N)+1) = 1;A(mod(i, N)+1, i) = 1;
end
L = diag(sum(A, 2)) - A; % 拉普拉斯矩阵
参考代码
(2) 一阶一致性协议
智能体动态模型:
[
\dot{x}i(t) = -\sum{j \in \mathcal{N}i} (x_i(t) - x_j(t))
]
目标:所有 (x_i(t)) 收敛到初始状态的均值 (\bar{x} = \frac{1}{N}\sum{i=1}^N x_i(0)).
% 初始状态
x0 = [3; -1; 4; 0; 2]; % 每个智能体的初始状态% 仿真参数
tspan = [0 10]; % 时间范围
dt = 0.01; % 时间步长% 定义动力学方程
odefun = @(t, x) -L * x;
[t, x] = ode45(odefun, tspan, x0);% 绘制收敛曲线
figure;
plot(t, x);
xlabel('Time (s)');
ylabel('State x_i(t)');
title('一阶一致性协议收敛过程');
grid on;
2. 离散时间一致性协议
若需离散时间模型(如通信间隔固定):
[
x_i(k+1) = x_i(k) + \epsilon \sum_{j \in \mathcal{N}i} (x_j(k) - x_i(k))
]
其中 (\epsilon) 为步长参数(需满足 (0 < \epsilon < 1/\Delta{\text{max}}),(\Delta_{\text{max}}) 为最大节点度)。
% 参数设置
epsilon = 0.1; % 需满足收敛条件
max_iter = 100; % 最大迭代次数% 初始化
x = x0;
x_history = zeros(N, max_iter+1);
x_history(:, 1) = x0;% 离散时间迭代
for k = 1:max_iterx = x - epsilon * L * x;x_history(:, k+1) = x;
end% 绘制结果
figure;
plot(0:max_iter, x_history');
xlabel('Iteration');
ylabel('State x_i(k)');
title('离散时间一致性协议收敛过程');
3. 含领导者的分层一致性
假设存在一个领导者(编号为1),其他智能体跟踪领导者状态:
[
\dot{x}i(t) = -\sum{j \in \mathcal{N}i} (x_i - x_j) - b_i (x_i - x{\text{leader}})
]
其中 (b_i = 1) 表示智能体 (i) 能直接接收领导者信息,否则 (b_i = 0).
% 定义领导者状态(假设为常数)
x_leader = 5;% 构建反馈矩阵 B
B = diag([1, 0, 0, 0, 0]); % 只有智能体1能观测到领导者% 修改拉普拉斯矩阵为 L + B
L_leader = L + B;% 动力学方程
odefun_leader = @(t, x) -L_leader * x + B * x_leader * ones(N, 1);
[t_leader, x_leader_sim] = ode45(odefun_leader, tspan, x0);% 绘制结果
figure;
plot(t_leader, x_leader_sim);
hold on;
plot(t_leader, x_leader*ones(size(t_leader)), 'k--', 'LineWidth', 2);
title('含领导者的分层一致性');
legend('Agent 1', 'Agent 2', 'Agent 3', 'Agent 4', 'Agent 5', 'Leader');
4. 时变拓扑一致性
模拟动态变化的网络拓扑(如随机切换的通信链路):
% 生成两个不同的拓扑(示例:环形和星型)
A1 = A; % 环形拓扑(之前的邻接矩阵)
A2 = [0 1 1 1 1; % 星型拓扑(中心节点1)1 0 0 0 0;1 0 0 0 0;1 0 0 0 0;1 0 0 0 0];
L1 = diag(sum(A1,2)) - A1;
L2 = diag(sum(A2,2)) - A2;% 定义时变拓扑函数(每2秒切换一次)
L_time_varying = @(t) (mod(t,4) < 2) * L1 + (mod(t,4) >= 2) * L2;% 动力学方程(使用ode45)
odefun_tv = @(t, x) -L_time_varying(t) * x;
[t_tv, x_tv] = ode45(odefun_tv, tspan, x0);% 绘制结果
figure;
plot(t_tv, x_tv);
title('时变拓扑下的一致性收敛');
5. 收敛性分析
(1) 理论验证
- 连续系统:拉普拉斯矩阵 (L) 的特征值决定收敛速度。若图连通,则 (L) 有单个零特征值,其余特征值实部正。
- 离散系统:需满足 ( \epsilon < \frac{2}{\lambda_{\text{max}}(L)} ).
% 计算拉普拉斯矩阵特征值
eig_L = eig(L);
disp('拉普拉斯矩阵特征值:');
disp(eig_L);% 验证离散系统收敛条件
lambda_max = max(eig(L));
epsilon_max = 2 / lambda_max;
fprintf('离散系统允许的最大步长: %.4f\n', epsilon_max);
(2) 数值验证
- 检查最终状态是否收敛到初始均值:
final_states = x(end, :);
mean_initial = mean(x0);
disp(['理论均值: ', num2str(mean_initial)]);
disp(['仿真终值: ', num2str(mean(final_states))]);
6. 扩展功能与改进方向
-
高阶一致性(二阶动力学):
% 二阶模型:位置和速度一致性 % 状态向量为 [x1, v1, x2, v2, ..., xN, vN]^T L_kron = kron(L, [0 0; 1 1]); % 扩展拉普拉斯矩阵 odefun_second_order = @(t, z) [z(2:2:end); -L_kron * z]; -
时延补偿:在协议中加入通信时延项:
[
\dot{x}i(t) = -\sum{j \in \mathcal{N}_i} (x_i(t-\tau) - x_j(t-\tau))
]
使用dde23求解时延微分方程。 -
鲁棒一致性:考虑噪声或不确定性的影响:
odefun_noise = @(t, x) -L * x + 0.1*randn(N,1); -
分布式事件触发控制:减少通信频率:
% 定义事件触发条件(例如状态误差超过阈值) event_threshold = 0.01;
7. 完整代码示例(一阶连续系统)
% 多智能体一致性仿真(基础版)
clc; clear; close all;% 1. 网络拓扑生成(随机图)
N = 6; % 智能体数量
A = rand(N,N) > 0.7; % 随机邻接矩阵(概率0.7连接)
A = triu(A,1) + triu(A,1)'; % 对称化
A(1:N+1:end) = 0; % 去除自环
L = diag(sum(A,2)) - A; % 拉普拉斯矩阵% 2. 初始状态
x0 = 10*randn(N,1); % 随机初始状态% 3. 仿真参数
tspan = [0 15];
options = odeset('RelTol', 1e-6, 'AbsTol', 1e-9);% 4. 求解微分方程
[t, x] = ode45(@(t,x) -L*x, tspan, x0, options);% 5. 绘制结果
figure;
plot(t, x);
xlabel('Time (s)');
ylabel('State');
title('多智能体一致性仿真');
grid on;% 6. 验证收敛到均值
final_mean = mean(x(end,:));
initial_mean = mean(x0);
fprintf('初始均值: %.4f\n终值均值: %.4f\n', initial_mean, final_mean);
代码输出说明
- 图1:各智能体状态随时间收敛到一致值。
- 终端输出:显示初始均值与仿真终值均值,验证收敛正确性。
参考文献
- Olfati-Saber, R., & Murray, R. M. (2004). Consensus problems in networks of agents with switching topology and time-delays. IEEE Transactions on Automatic Control.
- Ren, W., & Beard, R. W. (2008). Distributed consensus in multi-vehicle cooperative control. Springer.
通过修改网络拓扑、协议参数或动力学模型,可扩展此代码用于复杂场景研究(如无人机编队、智能电网频率同步等)。
相关文章:

matlab多智能体网络一致性研究
一个基于连续时间多智能体系统(Multi-Agent Systems, MAS)的一阶一致性协议的MATLAB仿真代码,包含网络拓扑建模、一致性协议设计和收敛性分析。代码支持固定拓扑和时变拓扑,适用于学术研究。 1. 基础模型与代码框架 (1) 网络拓扑…...

Unity(URP渲染管线)的后处理、动画制作、虚拟相机(Virtual Camera)
一、URP渲染管线 渲染管线是一系列渲染操作的集合,Unity提供了内置渲染管线(Built-In)和可编程渲染管线(SRP)两类渲染管线。内置渲染管线是Unity的默认渲染管线,其自定义选项有限。而可编程渲染管线可以通…...

C语言:在 Win 10 上,gcc 如何编译 gtk 应用程序
在 Windows 10 上使用 g(或 gcc)编译基于 GTK 的 C 语言程序是完全可行的,且相比 Tcc 更为推荐,因为 g(GNU 编译器套件)对 GTK 的支持更加完善,配置也更简单。以下是详细步骤和注意事项…...
)
阿里云CMH镜像迁移与SMC整机迁移对比及功能详解(同地域跨主体账号场景)
文章目录 一、核心功能对比二、CMH镜像迁移操作流程1.资源调研2.镜像共享3.迁移验证4.限制: 三、SMC整机迁移操作流程1.迁移源导入2.任务配置3.增量同步4.应用验证…...

用vue和go实现登录加密
前端使用CryptoJS默认加密方法: var pass CryptoJS.AES.encrypt(formData.password, key.value).toString()使用 CryptoJS.AES.encrypt() 时不指定加密模式和参数时,CryptoJS 默认会执行以下操作 var encrypted CryptoJS.AES.encrypt("明文&quo…...

政府数据开放试点企业如何抢占特许经营协议黄金席位
首席数据官高鹏律师团队 《中共中央办公厅 国务院办公厅关于 加快公共数据资源开发利用的意见》的落地,标志着数据从“封闭管理的行政资源”正式转变为“可流通的市场要素”。但机遇与风险从来是一枚硬币的两面——特许经营协议的黄金席位背后,隐藏着…...

CSS 锚点滑动效果的技术
CSS 锚点滑动效果的技术 引言 介绍锚点滑动效果的概念及其在网页设计中的重要性。简要说明 基本锚点链接 如何使用HTML中的<a>标签创建基本的锚点链接。示例代码: <a href"#section1">跳转到第一部分</a> <div id"section…...

mac-M系列芯片安装软件报错:***已损坏,无法打开。推出磁盘问题
因为你安装的软件在Intel 或arm芯片的mac上没有签名导致。 首先打开任何来源操作 在系统设置中配置,如下图: 2. 然后打开终端,输入: sudo spctl --master-disable然后输入电脑锁屏密码 打开了任何来源,还遇到已损坏…...

Echart地图数据源获取
DataV.GeoAtlas地理小工具系列 选择需要的区域地图,选中后输出即可: 地图钻取代码 <!DOCTYPE html> <html lang="en"> <head><meta charset="UTF-8"><title>map</title><style>html, body, #map{margin: 0;…...

GNSS数据自动化下载系统的设计与实现
摘要 本文详细介绍了三种不同设计的GNSS数据自动化下载系统,分别针对IGS观测数据、GRACE-FO Level-1B数据以及通过代理服务器获取数据的需求场景。系统采用Python实现,具备断点续传、完整性校验、异常处理和进度显示等核心功能。实验结果表明࿰…...

MySQL 中 JOIN 和子查询的区别与使用场景
目录 一、JOIN:表连接1.1 INNER JOIN:内连接1.2 LEFT JOIN:左连接1.3 RIGHT JOIN:右连接1.4 FULL JOIN:全连接二、子查询:嵌套查询2.1 WHERE 子句中的子查询2.2 FROM 子句中的子查询2.3 SELECT 子句中的子查询三、JOIN 和子查询的区别3.1 功能差异3.2 性能差异3.3 使用场…...

【深度学习-Day 12】从零认识神经网络:感知器原理、实现与局限性深度剖析
Langchain系列文章目录 01-玩转LangChain:从模型调用到Prompt模板与输出解析的完整指南 02-玩转 LangChain Memory 模块:四种记忆类型详解及应用场景全覆盖 03-全面掌握 LangChain:从核心链条构建到动态任务分配的实战指南 04-玩转 LangChai…...

谈谈未来iOS越狱或巨魔是否会消失
2024年10月的预测,先说结论: 巨魔iOS17.1消失概率为99%。 因为巨魔强依赖的漏洞就是一个签名漏洞,攻击面有限又经过2轮修复,第3次出现漏洞的概率极低。而越狱的话由于系统组件和服务较多,所以出现漏洞概率高攻击面多&…...
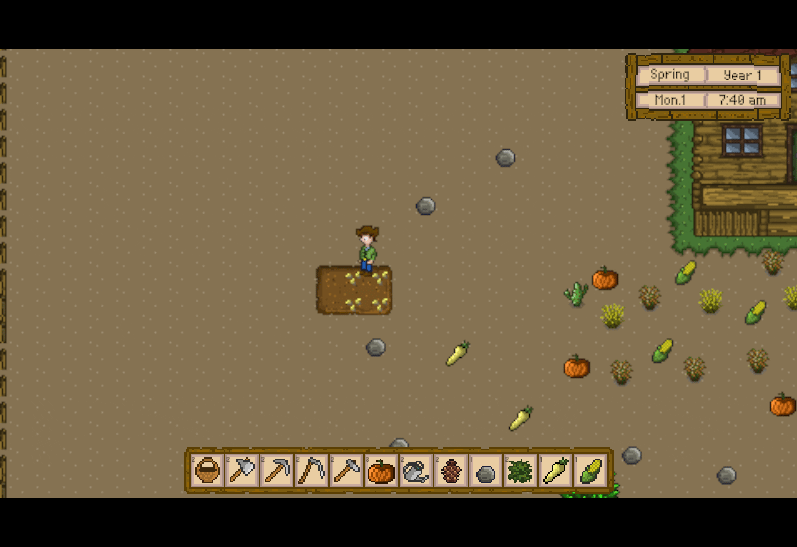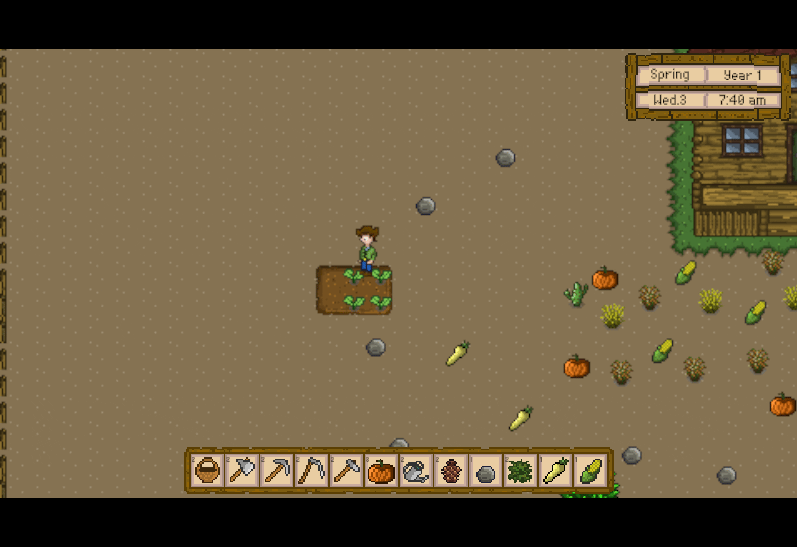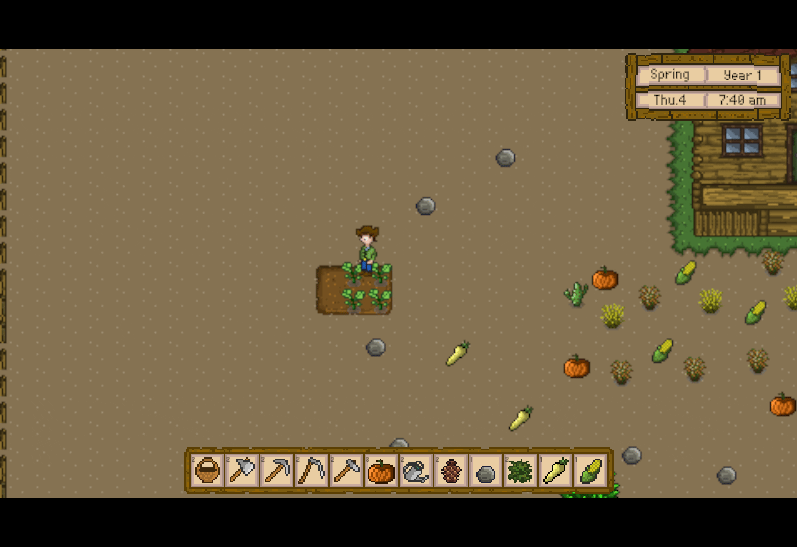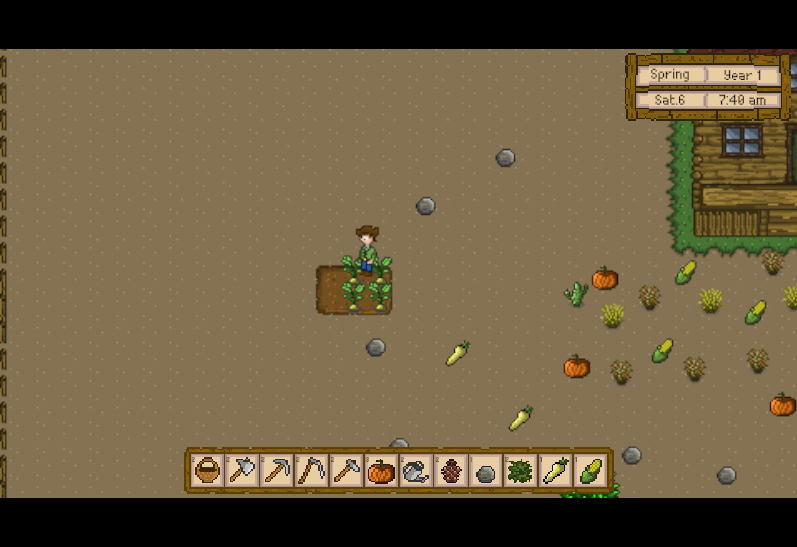
Unity3D仿星露谷物语开发43之农作物生长
1、目标 把防风草种子种在地里,并展示植物种子,防风草种子将随着时间变化而生长成植株。 2、创建Crop.cs脚本 在Assets -> Scripts下创建新的目录命名为Crop,在其下创建新的脚本命名为Crop.cs。 代码如下: using System.C…...

从0到1上手Kafka:开启分布式消息处理之旅
目录 一、Kafka 是什么 二、Kafka 的基础概念 2.1 核心术语解读 2.2 工作模式剖析 三、Kafka 的应用场景 四、Kafka 与其他消息队列的比较 五、Kafka 的安装与配置 5.1 环境准备 5.2 安装步骤 5.3 常见问题及解决 六、Kafka 的基本操作 6.1 命令行工具使用 6.1.1 …...
---运动程序多线程累加求和)
GTS-400 系列运动控制器板卡介绍(三十四)---运动程序多线程累加求和
运动控制器函数库的使用 运动控制器驱动程序、dll 文件、例程、Demo 等相关文件请通过固高科技官网下载,网 址为:www.googoltech.com.cn/pro_view-3.html 1 Windows 系统下动态链接库的使用 在 Windows 系统下使用运动控制器,首先要安装驱动程序。在安装前需要提前下载运动…...

Python爬虫如何应对网站的反爬加密策略?
在当今的互联网环境中,网络爬虫已经成为数据采集的重要工具之一。然而,随着网站安全意识的不断提高,反爬虫技术也越来越复杂,尤其是数据加密策略的广泛应用,给爬虫开发者带来了巨大的挑战。本文将详细介绍Python爬虫如…...

第一次经历项目上线
这几天没写csdn,因为忙着项目上线的问题,我这阶段改了非常多的前端bug哈哈哈哈,说几个比较好的bug思想! 这个页面算是我遇到的比较大的bug,因为我一开始的逻辑都写好了,询价就是在点击快递公司弹出弹框的时…...

Conda配置完全指南——Windows系统Anaconda/Miniconda的安装、配置、基础使用、清理缓存空间和Pycharm/VSCode配置指南
本文同步发布在个人博客: Conda配置完全指南Conda 是一个开源的跨平台包管理与环境管理工具,广泛应用于数据科学、机器学习及 Python 开发领域。它不仅能帮助用户快速安装、更新和卸载第三方库,还能创建相互隔离的虚拟环境,解决不…...

Quasar组件 Carousel走马灯
通过对比两个q-carousel组件来,了解该组件的属性 官方文档请参阅:Carousel 预览 源代码 <template><div class"q-pa-md"><div class"q-gutter-md"><q-carouselv-model"slide"transition-prev&quo…...

AI日报 - 2024年5月17日
🌟 今日概览 (60秒速览) ▎🤖 大模型前沿 | OpenAI推出自主编码代理Codex;Google DeepMind发布Gemini驱动的编码代理AlphaEvolve,能设计先进算法;Meta旗舰AI模型Llama 4 Behemoth发布推迟。 Codex能并行处理多任务&…...
数据的构建及简单分析)
R语言数据框(datafram)数据的构建及简单分析
代码完成的功能: 创建数据集(数据框), 写入到文件中, 显示数据, 分组计算平均年龄, 在Rstudio中,创建R markdown或R notebook文件运行。以下是添加了注释的完整R代码࿰…...

风控域——风控决策引擎系统设计
摘要 本文详细介绍了风控决策引擎系统的设计与应用。决策引擎系统是一种智能化工具,可自动化、数据驱动地辅助或替代人工决策,广泛应用于金融、医疗、营销、风控等领域。文章阐述了决策引擎的核心功能,包括自动化决策、动态规则管理、实时处…...

CAPL Class: TcpSocket (此类用于实现 TCP 网络通信 )
目录 Class: TcpSocketacceptopenclosebindconnectgetLastSocketErrorgetLastSocketErrorAsStringlistenreceivesendsetSocketOptionshutdown函数调用的基本流程服务器端的基本流程客户端的基本流程Class: TcpSocket学习笔记。来自CANoe帮助文档。 Class: TcpSocket accept /…...

数据分析 —— 数据预处理
一、什么是数据预处理 数据预处理(Data Preprocessing)是数据分析和机器学习中至关重要的步骤,旨在将原始数据转换为更高质量、更适合分析或建模的形式。由于真实世界的数据通常存在不完整、不一致、噪声或冗余等问题,预处理可以…...

软件架构风格系列(4):事件驱动架构
文章目录 前言一、从“用户下单”场景看懂事件驱动核心概念(一)什么是事件驱动架构?(二)核心优势:解耦与异步的双重魔法 二、架构设计图:三要素构建事件流转闭环三、Java实战:从简单…...

windows系统各版本下载
以下各版本Windows系统链接来自网友整理,请通过迅雷或者其他支持ED2K或BT的下载工具进行下载。 注:以下为原版系统,未激活、非破解版,仅供下载体验学习,请勿从事商业活动。 Windows 11 Windows 11 (consumer editions…...

arduino平台读取鼠标光电传感器
鼠标坏掉了,大抵是修不好了。(全剧终—) 但是爱动手的小明不会浪费这个鼠标,确认外观没有明显烧毁痕迹后,尝试从电路板上利用光电传感器进行位移的测量,光电传感器(型号:FCT3065&am…...

【Linux网络】网络层
网络层 在复杂的网络环境中确定一个合适的路径 IP 协议 IPV4 点分十进制[0,255].[0,255].[0,255].[0,255]IPV6 IP地址目标网格目标主机 基本概念 主机:配有IP地址,但是不进行路由控制的设备;路由器:即配有IP地址,又能进行路由控制;节点:主机和路由器的统称。 两个问题 路…...

力扣-98.验证二叉搜索树
题目描述 给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。 有效 二叉搜索树定义如下: 节点的左子树只包含 小于 当前节点的数。节点的右子树只包含 大于 当前节点的数。所有左子树和右子树自身必须也是二叉搜索树。 class Solutio…...
