【CSS】使用 CSS 绘制三角形
一、Border 边框法(最常用)
原理:通过设置元素的宽高为 0,利用透明边框相交形成三角形。
.triangle {width: 0;height: 0;border-left: 50px solid transparent; /* 左侧边框透明 */border-right: 50px solid transparent; /* 右侧边框透明 */border-bottom: 100px solid red; /* 下边框显示颜色 */
}
• 关键属性:width: 0; height: 0; + border-* 组合
• 方向控制:
• 向上:border-bottom 有颜色,其他透明
• 向下:border-top 有颜色,其他透明
• 向左/右:设置对应边框颜色(如左三角形:border-right 有颜色)
• 优点:兼容性极佳(包括 IE8+),代码简单
• 缺点:无法在三角形内部添加内容
等腰直角三角形:
.triangle {width: 0;height: 0;border-left: 50px solid transparent;border-right: 50px solid lightblue;border-bottom: 50px solid lightblue;border-top: 50px solid transparent;
}

原理
- 构建一个正方形
- 为正方形添加不同方向的边框
- 将正方形的宽高设置为0
- 设置三个边框为透明
// 1
.triangle {width: 50px;height: 50px;background-color: red;
}// 2
.trangle {// ....border-left: 50px solid yellow;border-right: 50px solid green;border-bottom: 50px solid lightblue;border-top: 50px solid pink;
}// 3
.trangle {// ....width: 0;height: 0;
}// 4
.trangle {// ....border-left: 50px solid transparent;border-right: 50px solid transparent;border-bottom: 50px solid transparent;border-top: 50px solid pink;
}
二、Clip-Path 裁剪法
原理:通过裁剪元素的可见区域形成三角形。
.triangle {width: 100px;height: 100px;background: red;clip-path: polygon(50% 0%, 0% 100%, 100% 100%); /* 定义三个顶点坐标 */
}
• 关键属性:clip-path: polygon(x1 y1, x2 y2, x3 y3)
• 方向控制:调整坐标点顺序(如 polygon(0% 0%, 100% 50%, 0% 100%) 为右三角形)
• 优点:支持任意形状,容器可添加内容,响应式自适应
• 缺点:低版本浏览器兼容性差(如 IE 不支持)
三、渐变法(Linear/Conic Gradient)
原理:利用线性或角向渐变的颜色断点生成三角形。
.triangle {width: 100px;height: 100px;background: linear-gradient(45deg, red 50%, transparent 50%);
}
• 关键属性:linear-gradient() 或 conic-gradient()
• 方向控制:调整渐变角度(如 to bottom right)或颜色断点位置
• 优点:支持复杂渐变效果,容器保留原有尺寸
• 缺点:实现复杂度高,需调试角度和断点
四、字符法(特殊场景)
原理:使用 Unicode 字符直接显示三角形符号。
<div class="triangle">▼</div>
.triangle {font-size: 50px;color: red;
}
• 关键属性:font-family + Unicode 字符(如 ▲ ▼ ◀ ▶)
• 优点:无需 CSS 绘制
• 缺点:依赖字体库,样式控制有限
方案对比与选型建议
| 方法 | 兼容性 | 灵活性 | 内容支持 | 适用场景 |
|---|---|---|---|---|
| Border 边框法 | ⭐⭐⭐⭐ | ⭐⭐ | ❌ | 简单箭头、工具提示 |
| Clip-Path | ⭐⭐ | ⭐⭐⭐ | ✅ | 复杂形状、响应式设计 |
| 渐变法 | ⭐⭐⭐ | ⭐⭐ | ✅ | 渐变效果、背景装饰 |
| 字符法 | ⭐⭐⭐⭐ | ❌ | ✅ | 快速实现、无需精确控制 |
推荐优先级:
- Border 边框法(兼容性强,代码简洁)
- Clip-Path 法(现代项目首选,灵活易维护)
- 渐变法(特殊视觉效果需求)
注意事项
• 等边三角形:需计算边框宽度比例(如底边 100px,左右边框 ≈87px)
• 性能优化:避免频繁使用 clip-path 或渐变,可能导致渲染性能下降
• 浏览器前缀:部分属性需加 -webkit- 前缀(如 clip-path)
相关文章:

【CSS】使用 CSS 绘制三角形
一、Border 边框法(最常用) 原理:通过设置元素的宽高为 0,利用透明边框相交形成三角形。 .triangle {width: 0;height: 0;border-left: 50px solid transparent; /* 左侧边框透明 */border-right: 50px solid transparent; /* …...

信奥赛-刷题笔记-栈篇-T2-P3056括号调整问题0518
总题单 本部分总题单如下 【腾讯文档】副本-CSP-JSNOI 题单 (未完待续) https://docs.qq.com/sheet/DSmJuVXR4RUNVWWhW?tabBB08J2 栈篇题单 P3056 [USACO12NOV] Clumsy Cows S https://www.luogu.com.cn/problem/P3056 题目描述 Bessie the cow is trying to type …...

生命之树--树形dp
1.树形dp--在dfs遍历树的同时dp,从上到下递归,到叶子是边界条件 https://www.luogu.com.cn/problem/P8625 #include<bits/stdc.h> using namespace std; #define N 100011 typedef long long ll; typedef pair<ll,int> pii; int n,c; ll …...

inverse-design-of-grating-coupler-3d
一、设计和优化3D光栅耦合器 1.1 代码讲解 通过预定义的环形间距参数(distances数组),在FDTD中生成椭圆光栅结构,并通过用户交互确认几何正确性后,可进一步执行参数扫描优化。 # os:用于操作系统相关功能(如文件路径操作) import os import sys# lumapi:Lumerical 的…...

Science Robotics 封面论文:基于形态学开放式参数化的仿人灵巧手设计用于具身操作
人形机械手具有无与伦比的多功能性和精细运动技能,使其能够精确、有力和稳健地执行各种任务。在古生物学记录和动物王国中,我们看到了各种各样的替代手和驱动设计。了解形态学设计空间和由此产生的涌现行为不仅可以帮助我们理解灵巧的作用及其演变&#…...

普通用户的服务器连接与模型部署相关记录
普通用户的服务器连接与模型部署相关记录 一、从登录到使用自己的conda 1.账号登陆: ssh xxx172.31.226.236 2.下载与安装conda: 下载conda: wget -c https://repo.anaconda.com/archive/Anaconda3-2023.03-1-Linux-x86_64.sh 安装con…...

DSU-Net
目录 Abstract 摘要 DSU-Net 模型框架 编码器 轻量级适配器模块 特征融合与协作 解码器 模型优势 实验 代码 总结 Abstract DSU-Net is an improved U-Net model based on DINOv2 and SAM2. It addresses the limitations of existing image segmentation models …...

深入解析Python中的Vector2d类:从基础实现到特殊方法的应用
引言 在Python面向对象编程中,特殊方法(或称魔术方法)是实现对象丰富行为的关键。本文将以Vector2d类为例,详细讲解如何通过特殊方法为自定义类添加多种表示形式和操作能力。 Vector2d类的基本行为 Vector2d类是一个二维向量类…...

2025年- H30-Lc138- 141.环形链表(快慢指针,快2慢1)---java版
1.题目描述 2.思路 弗洛伊德算法(快慢指针 3.代码实现 public boolean hasCycle(ListNode head) {//1.如果空节点或者只有一个节点,都说明没有环,返回falseif(headnull||head.nextnull){return false;}//2.定义快慢指针,都从头…...

LoadBarWorks:一款赛博风加载动画生成器的构建旅程
我正在参加CodeBuddy「首席试玩官」内容创作大赛,本文所使用的 CodeBuddy 免费下载链接:腾讯云代码助手 CodeBuddy - AI 时代的智能编程伙伴 项目缘起:赛博与实用的结合 在日常开发中,我经常需要为不同的项目添加加载动画&#x…...

SAP集团内部公司间交易自动开票
SAP集团内部公司间交易自动开票(非STO/EDI模式) 集团内部公司间采购与销售业务,在确认相应单据无误后,为减少人工开票业务, 可以用系统标准功能来实现自动开票。 1.采购发票自动开票(ERS) T-CODE:BP,勾选“基于收货的发票校验”、“自动G…...

【YOLO(txt)格式转VOC(xml)格式数据集】以及【制作VOC格式数据集 】
1.txt—>xml转化代码 如果我们手里只有YOLO标签的数据集,我们要进行VOC格式数据集的制作首先要进行标签的转化,以下是标签转化的脚本。 其中picPath为图片所在文件夹路径; txtPath为你的YOLO标签对应的txt文件所在路径; xmlPa…...

WSL 安装 Debian 12 后,如何安装图形界面 X11 ?
在 Debian Linux 系统中安装 X11(X Window System),可以按照以下步骤进行操作: 一、确认系统版本和硬件支持 首先,你需要确认自己的 Debian 系统版本,可使用以下命令: cat /etc/debian_versi…...

Linux 的 UDP 网络编程 -- 回显服务器,翻译服务器
目录 1. 回显服务器 -- echo server 1.1 相关函数介绍 1.1.1 socket() 1.1.2 bind() 1.1.3 recvfrom() 1.1.4 sendto() 1.1.5 inet_ntoa() 1.1.6 inet_addr() 1.2 Udp 服务端的封装 -- UdpServer.hpp 1.3 服务端代码 -- UdpServer.cc 1.4 客户端代码 -- UdpClient.…...

C++笔试题(金山科技新未来训练营):
题目分布: 17道单选(每题3分)3道多选题(全对3分,部分对1分)2道编程题(每一道20分)。 不过题目太多,就记得一部分了: 单选题: static变量的初始…...

【RabbitMQ】 RabbitMQ高级特性(二)
文章目录 一、重试机制1.1、重试配置1.2、配置交换机&队列1.3、发送消息1.4、消费消息1.5、运行程序1.6、 手动确认 二、TTL2.1、设置消息的TTL2.2、设置队列的TTL2.3、两者区别 三 、死信队列6.1 死信的概念3.2 代码示例3.2.1、声明队列和交换机3.2.2、正常队列绑定死信交…...

大数据技术全景解析:HDFS、HBase、MapReduce 与 Chukwa
大数据技术全景解析:HDFS、HBase、MapReduce 与 Chukwa 在当今这个信息爆炸的时代,大数据已经成为企业竞争力的重要组成部分。从电商的用户行为分析到金融的风险控制,从医疗健康的数据挖掘到智能制造的实时监控,大数据技术无处不…...

电子电路:什么是电流离散性特征?
关于电荷的量子化,即电荷的最小单位是电子的电荷量e。在宏观电路中,由于电子数量极大,电流看起来是连续的。但在微观层面,比如纳米器件或单电子晶体管中,单个电子的移动就会引起可观测的离散电流。 还要提到散粒噪声,这是电流离散性的表现之一。当电流非常小时,例如在二…...
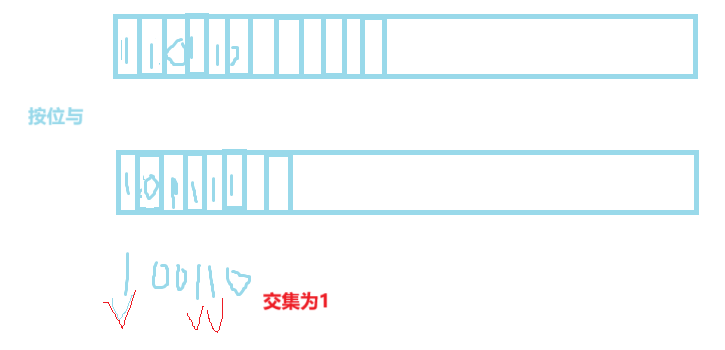
深入理解位图(Bit - set):概念、实现与应用
目录 引言 一、位图概念 (一)基本原理 (二)适用场景 二、位图的实现(C 代码示例) 三、位图应用 1. 快速查找某个数据是否在一个集合中 2. 排序 去重 3. 求两个集合的交集、并集等 4. 操作系…...

猫番阅读APP:丰富资源,优质体验,满足你的阅读需求
猫番阅读APP是一款专为书籍爱好者设计的移动阅读应用,致力于提供丰富的阅读体验和多样化的书籍资源。它不仅涵盖了小说、非虚构、杂志等多个领域的电子书,还提供了个性化推荐、书架管理、离线下载等功能,满足不同读者的阅读需求。无论是通勤路…...

Java文件读写程序
1.引言 在日常的软件开发中,文件操作是常见的功能之一。不仅要了解如何读写文件,更要知道如何安全地操作文件以避免程序崩溃或数据丢失。这篇文章将深入分析一个简单的 Java 文件读写程序 Top.java,包括其基本实现、潜在问题以及改进建议&am…...

深入解析Java事件监听机制与应用
Java事件监听机制详解 一、事件监听模型组成 事件源(Event Source) 产生事件的对象(如按钮、文本框等组件) 事件对象(Event Object) 封装事件信息的对象(如ActionEvent包含事件源信息…...

MetaMask安装及使用-使用水龙头获取测试币的坑?
常见的异常有: 1.unable to request drip, please try again later. 2.You must hold at least 1 LINK on Ethereum Mainnet to request native tokens. 3.The address provided does not have sufficient historical activity or balance on the Ethereum Mainne…...

AI:OpenAI论坛分享—《AI重塑未来:技术、经济与战略》
AI:OpenAI论坛分享—《AI重塑未来:技术、经济与战略》 导读:2025年4月24日,OpenAI论坛全面探讨了 AI 的发展趋势、技术范式、地缘政治影响以及对经济和社会的广泛影响。强调了 AI 的通用性、可扩展性和高级推理能力,以…...

Linux配置vimplus
配置vimplus CentOS的配置方案很简单,但是Ubuntu的解决方案网上也很多但是有效的很少,尤其是22和24的解决方案,在此我整理了一下我遇到的问题解决方法 CentOS7 一键配置VimForCPP 基本上不会有什么特别难解决的报错 sudo yum install vims…...

服务端HttpServletRequest、HttpServletResponse、HttpSession
一、概述 在JavaWeb 开发中,获取客户端传递的参数至关重要。http请求是客户端向服务端发起数据传输协议,主要包含包含请求行、请求头、空行和请求体四个部分,在这四部分中分别携带客户端传递到服务端的数据。常见的http请求方式有get、post、…...

实验九视图索引
设计性实验 1. 创建视图V_A包括学号,姓名,性别,课程号,课程名、成绩; 一个语句把学号103 课程号3-105 的姓名改为陆君茹1,性别为女 ,然后查看学生表的信息变化,再把上述数据改为原…...

git 本地提交后修改注释
dos命令行进入目录,idea可以点击Terminal 进入命令行 git commit --amend -m "修改内容"...

面向具身智能的视觉-语言-动作模型(VLA)综述
具身智能被广泛认为是通用人工智能(AGI)的关键要素,因为它涉及控制具身智能体在物理世界中执行任务。在大语言模型和视觉语言模型成功的基础上,一种新的多模态模型——视觉语言动作模型(VLA)已经出现&#…...

Thrust库中的Gather和Scatter操作
Thrust库中的Gather和Scatter操作 Thrust是CUDA提供的一个类似于C STL的并行算法库,其中包含两个重要的数据操作:gather(聚集)和scatter(散开)。 Gather操作 Gather操作从一个源数组中按照指定的索引收集元素到目标数组中。 函数原型: t…...
