深入理解动态规划:从斐波那契数列到最优子结构
引言
动态规划(Dynamic Programming, DP)是算法设计中一种非常重要的思想,广泛应用于解决各类优化问题。许多看似复杂的问题,通过动态规划的视角分析,往往能找到高效的解决方案。本文将系统介绍动态规划的核心概念,通过经典案例展示其应用,并探讨如何识别和解决动态规划问题。
一、什么是动态规划?
动态规划是一种分治思想的延伸,主要用于解决具有重叠子问题和最优子结构性质的问题。与普通的分治算法不同,动态规划会保存已解决的子问题的答案,避免重复计算,从而显著提高效率。
动态规划通常用于两类问题:
- 优化问题:寻找问题的最优解(最大或最小值)
- 组合问题:计算满足特定条件的解的数量
2. 动态规划的核心思想
动态规划适用于具有以下两个关键性质的问题:
- 重叠子问题(Overlapping Subproblems) :问题可以分解为若干子问题,且子问题之间存在重复计算。
- 最优子结构(Optimal Substructure) :问题的最优解可以由子问题的最优解推导而来。
动态规划通常有两种实现方式:
- 自顶向下(Top-Down) :递归 + 记忆化(Memoization)
- 自底向上(Bottom-Up) :迭代 + DP 表
3. 从斐波那契数列理解动态规划
3.1 递归解法的问题
斐波那契数列定义:
- F(0)=0F(0)=0
- F(1)=1F(1)=1
- F(n)=F(n−1)+F(n−2)F(n)=F(n−1)+F(n−2) (n≥2n≥2)
递归实现(C++) :
int fib(int n) {if (n <= 1) return n;return fib(n - 1) + fib(n - 2);
}
问题:时间复杂度 O(2n),存在大量重复计算(如 fib(3) 被多次计算)。
3.2 记忆化递归(Top-Down DP)
使用数组或哈希表存储已计算的结果:
int fibMemo(int n, vector<int>& memo) {if (n <= 1) return n;if (memo[n] != -1) return memo[n];memo[n] = fibMemo(n - 1, memo) + fibMemo(n - 2, memo);return memo[n];
}int fib(int n) {vector<int> memo(n + 1, -1);return fibMemo(n, memo);
}
优化后时间复杂度:O(n),空间复杂度 O(n)。
3.3 自底向上 DP(Bottom-Up DP)
用迭代方式计算:
int fib(int n) {if (n <= 1) return n;vector<int> dp(n + 1);dp[0] = 0;dp[1] = 1;for (int i = 2; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];
}
进一步优化空间(仅保留前两个状态):
int fib(int n) {if (n <= 1) return n;int a = 0, b = 1;for (int i = 2; i <= n; i++) {int c = a + b;a = b;b = c;}return b;
}
时间复杂度:O(n),空间复杂度:O(1)。
4. 最优子结构与状态转移方程
动态规划的关键在于:
- 定义状态(如
dp[i]表示第i个问题的解)。 - 找到状态转移方程(递推关系)。
- 初始化边界条件(如
dp[0]和dp[1])。
例题 1:爬楼梯(LeetCode 70)
题目链接
-
问题:每次可以爬 1 或 2 阶台阶,求爬到第
n阶的方法数。 -
状态定义:
dp[i]表示爬到第i阶的方法数。 -
状态转移方程:
dp[i]=dp[i−1]+dp[i−2]dp[i]=dp[i−1]+dp[i−2]
-
C++ 实现:
int climbStairs(int n) {if (n <= 2) return n;int a = 1, b = 2;for (int i = 3; i <= n; i++) {int c = a + b;a = b;b = c;}return b;
}
例题 2:最大子数组和(LeetCode 53)
题目链接
-
问题:给定整数数组
nums,求连续子数组的最大和。 -
状态定义:
dp[i]表示以nums[i]结尾的最大子数组和。 -
状态转移方程:
dp[i]=max(dp[i−1]+nums[i],nums[i])dp[i]=max(dp[i−1]+nums[i],nums[i]) -
C++ 实现:
int maxSubArray(vector<int>& nums) {int maxSum = nums[0], currSum = nums[0];for (int i = 1; i < nums.size(); i++) {currSum = max(currSum + nums[i], nums[i]);maxSum = max(maxSum, currSum);}return maxSum;
}
例题 3:最长递增子序列(LeetCode 300)
题目链接
-
问题:求数组中最长的严格递增子序列长度。
-
状态定义:
dp[i]表示以nums[i]结尾的最长递增子序列长度。 -
状态转移方程:
dp[i]=max(dp[j]+1)其中0≤j<i且nums[j]<nums[i]dp[i]=max(dp[j]+1)其中0≤j<i且nums[j]<nums[i] -
C++ 实现:
int lengthOfLIS(vector<int>& nums) {int n = nums.size();vector<int> dp(n, 1);int maxLen = 1;for (int i = 1; i < n; i++) {for (int j = 0; j < i; j++) {if (nums[j] < nums[i]) {dp[i] = max(dp[i], dp[j] + 1);}}maxLen = max(maxLen, dp[i]);}return maxLen;
}
5. 动态规划的优化技巧
- 空间优化:如斐波那契数列问题,仅存储前两个状态。
- 状态压缩:如 0-1 背包问题,可将二维 DP 优化为一维。
- 贪心优化:如股票买卖问题,可结合贪心思想优化 DP。
6. 总结
动态规划的核心在于:
- 定义状态(
dp[i]表示什么?) - 找到状态转移方程(如何递推?)
- 初始化边界条件(
dp[0]和dp[1]的值?)
通过斐波那契数列、爬楼梯、最大子数组和、最长递增子序列等经典问题,我们可以逐步掌握动态规划的解题思路。后续可进一步学习:
- 背包问题(LeetCode 416, 494)
- 股票买卖问题(LeetCode 121, 122, 123)
- 字符串 DP(LeetCode 72, 1143)
希望本文能帮助你深入理解动态规划,并在算法竞赛和面试中灵活运用!🚀
相关文章:

深入理解动态规划:从斐波那契数列到最优子结构
引言 动态规划(Dynamic Programming, DP)是算法设计中一种非常重要的思想,广泛应用于解决各类优化问题。许多看似复杂的问题,通过动态规划的视角分析,往往能找到高效的解决方案。本文将系统介绍动态规划的核心概念,通过经典案例展…...

基于Linux环境实现Oracle goldengate远程抽取MySQL同步数据到MySQL
基于Linux环境实现Oracle goldengate远程抽取MySQL同步数据到MySQL 场景说明: 先有项目需要读取生产库数据,但是不能直接读取生产库数据,需要把生产数据同步到一个中间库,下游系统从中间库读取数据。 生产库mysql - OGG - 中间库…...

电子电路原理第十六章(负反馈)
1927年8月,年轻的工程师哈罗德布莱克(Harold Black)从纽约斯塔顿岛坐渡轮去上班。为了打发时间,他粗略写下了关于一个新想法的几个方程式。后来又经过反复修改, 布莱克提交了这个创意的专利申请。起初这个全新的创意被认为像“永动机”一样愚蠢可笑,专利申请也遭到拒绝。但…...

Go语言数组的定义与操作 - 《Go语言实战指南》
在 Go 语言中,数组(Array) 是一种定长、同类型的集合。它在内存中是连续分布的,适合用于性能敏感的场景。 一、数组的定义 数组的基本语法如下: var 数组名 [长度]元素类型 示例: var nums [5]int …...

物联网简介:万物互联的未来图景
物联网简介:万物互联的未来图景 引言 在科技飞速发展的今天,我们身边的一切似乎都在悄然发生变化。从清晨智能闹钟根据你的睡眠状态自动唤醒,到厨房里的咖啡机在你起床前已经煮好咖啡;从城市交通系统通过实时数据优化红绿灯时长…...

命令拼接符
Linux多命令顺序执行符号需要记住5个 【|】【||】【 ;】 【&】 【&&】 ,在命令执行里面,如果服务器疏忽大意没做限制,黑客通过高命令拼接符,可以输入很多非法的操作。 ailx10 网络安全优秀回答者 互联网…...

【通用智能体】Lynx :一款基于终端的纯文本网页浏览器
Lynx :一款基于终端的纯文本网页浏览器 一、Lynx简介二、应用场景及案例场景 1:服务器端网页内容快速查看场景 2:网页内容快速提取场景 3:表单提交与自动化交互场景 4:网络诊断与调试场景 5:辅助工具适配 三…...

51单片机的lcd12864驱动程序
#include <reg51.h> #include <intrins.h>#define uchar...

GStreamer (三)常⽤插件
常⽤插件 1、Source1.1、filesrc1.2. videotestsrc1.3. v4l2src1.4. rtspsrc和rtspclientsink 2、 Sink2.1. filesink2.2. fakesink2.3. xvimagesink2.4. kmssink2.5. waylandsink2.6. rkximagesink2.7. fpsdisplaysink 3 、视频推流/拉流3.1. 本地推流/拉流3.1.1 USB摄像头3.1…...

Java POJO接收前端null值设置
在 Java 中,若要让 price 字段接收前端传递的 null 值,只需确保以下几点: 1. 使用包装类型 Double 你的 price 字段已经是包装类型 Double(而不是基本类型 double),这天然支持 null 值。基本类型 double …...

详细总结和讲解redis的基本命令
Redis 是一个开源的内存数据结构存储系统,它可以用作数据库、缓存和消息中间件。Redis 支持多种类型的数据结构,如字符串(Strings)、哈希(Hashes)、列表(Lists)、集合(Se…...

Linux 内核等待机制详解:prepare_to_wait_exclusive 与 TASK_INTERRUPTIBLE
1. prepare_to_wait_exclusive 函数解析 1.1 核心作用 prepare_to_wait_exclusive 是 Linux 内核中用于将进程以独占方式加入等待队列的关键函数,其主要功能包括: 标记独占等待:通过设置 WQ_FLAG_EXCLUSIVE 标志,表明此等待条目是独占的。 安全入队:在自旋锁保护下,将条…...

蓝桥杯2300 质数拆分
问题描述 将 2022 拆分成不同的质数的和,请问最多拆分成几个? 01背包问题 #include<iostream> #include<cmath> #include<algorithm> using namespace std;int prime[2025]; int dp[2025]; //dp[j]:和为 j 时的最多拆分…...

软件架构风格系列(2):面向对象架构
文章目录 引言一、什么是面向对象架构风格1. 定义与核心概念2. 优点与局限性二、业务建模:用对象映射现实世界(一)核心实体抽象1. 员工体系2. 菜品体系 (二)封装:隐藏实现细节 三、继承实战:构建…...

ngx_http_random_index_module 模块概述
一、使用场景 随机内容分发 当同一目录下存放多份等价内容(如多张轮播图、不同版本静态页面等)时,可通过随机索引实现负载均衡或流量分散。A/B 测试 通过目录请求自动随机分配用户到不同测试组,无需后端逻辑参与。动态“首页”选…...

go-zero(十八)结合Elasticsearch实现高效数据检索
go-zero结合Elasticsearch实现高效数据检索 1. Elasticsearch简单介绍 Elasticsearch(简称 ES) 是一个基于 Lucene 库 构建的 分布式、开源、实时搜索与分析引擎,采用 Apache 2.0 协议。它支持水平扩展,能高效处理大规模数据的存…...
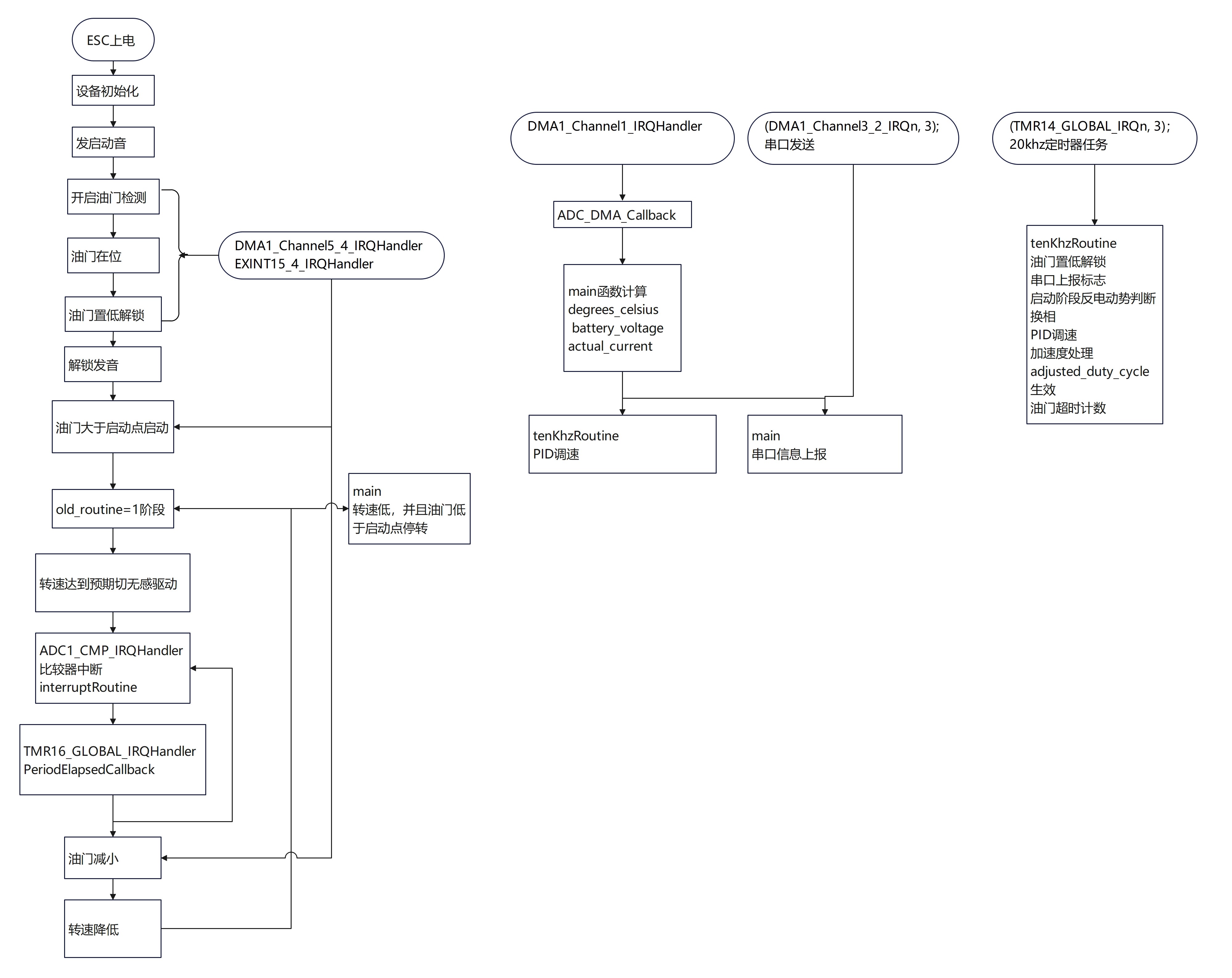
AM32电调学习解读九:ESC上电启动关闭全流程波形分析
这是第九篇,前面的文章把各个模块的实现都介绍了一轮,本章是从运行的角度结合波形图,把整个流程走一遍。 先看下一运行的配置,我把一些配置关闭了,这样跑起来会好分析一些,不同配置跑起来效果会有差异。使用…...

怎么打包发布到npm?——从零到一的详细指南
怎么打包发布到npm?——从零到一的详细指南 目录 怎么打包发布到npm?——从零到一的详细指南一、准备工作1. 注册 npm 账号2. 安装 Node.js 和 npm 二、初始化项目三、编写你的代码四、配置 package.json五、打包你的项目六、登录 npm七、发布到 npm八、…...

NX二次开发C#---遍历当前工作部件实体并设置颜色
该代码片段展示了如何在Siemens NX软件中使用C#进行自动化操作。通过NXOpen和UFSession API,代码首先获取当前工作部件,并遍历其中的所有实体。对于每个实体,代码检查其类型和子类型是否为“实体”,如果是,则将其颜色设…...

如何用体育数据做分析:从基础统计到AI驱动的决策科学
一、体育数据分析的演进与价值创造 体育数据分析已从简单的比分记录发展为融合统计学、计算机科学和运动科学的交叉学科。现代体育组织通过数据分析可以实现: 竞技表现提升:勇士队利用投篮热图优化战术布置 商业价值挖掘:曼联通过球迷行为数…...

09、底层注解-@Import导入组件
09、底层注解-Import导入组件 Import是Spring框架中的一个注解,用于将组件导入到Spring的应用上下文中。以下是Import注解的详细介绍: #### 基本用法 - **导入配置类** java Configuration public class MainConfig { // 配置内容 } Configuration Impo…...

【notes】VScode 使用总结
文章目录 扩展 c/cwindows7 系统下 c/c 自动升级导致的插件无法正常使用 设置 文件格式设置打开文件的默认格式 扩展 c/c windows7 系统下 c/c 自动升级导致的插件无法正常使用 问题 1. c/c扩展的1.25.x版本不再支持windows7 系统,当设置VScode自动升级拓展插件时…...

【论文阅读】KIMI K1.5: SCALING REINFORCEMENT LEARNING WITH LLMS
KIMI K1.5: SCALING REINFORCEMENT LEARNING WITH LLMS Scaling的解释: 通过系统性的方法扩展强化学习算法的能力,使其能够处理更复杂的问题、更大的状态/动作空间、更长的训练周期或更高效的资源利用 原文摘要: 研究背景与问题定位 传统预训…...

云服务器开发软件操作步骤
云服务器开发软件的主要步骤。通常,这包括选择云服务提供商、配置服务器环境、开发、测试、部署、维护等阶段。每个阶段都需要详细解释,可能需要分步骤说明。例如,选择云服务提供商时,需要考虑AWS、阿里云、腾讯云等,比…...

Qwen3 - 0.6B与Bert文本分类实验:深度见解与性能剖析
Changelog [25/04/28] 新增Qwen3-0.6B在Ag_news数据集Zero-Shot的效果。新增Qwen3-0.6B线性层分类方法的效果。调整Bert训练参数(epoch、eval_steps),以实现更细致的观察,避免严重过拟合的情况。 TODO: 利用Qwen3-0.6…...

4.6 sys模块
sys --- 仅作了解 面试之前冲击一下 python的垃圾回收机制 import sys # 1. api_version : 获取python的内部版本号 print(sys.api_version) #1013 # 2. copyright: 获取cpython的版本 print(sys.copyright) #3.getfilesystemencoding() getdefaultencoding():获…...

UWB定位方案在水力发电站人员安全的应用推荐
一、行业应用背景 水力发电站具有环境复杂(金属设备密集、高温高压区域多)、安全风险高(人员误入高危区域易引发事故)等特点,传统定位技术难以满足精度与可靠性要求。品铂科技基于UWB的高精度定位系统已在多…...

青少年编程与数学 02-019 Rust 编程基础 16课题、包、单元包及模块
青少年编程与数学 02-019 Rust 编程基础 16课题、包、单元包及模块 一、包1. **什么是 Crate?**2. **Crate 的类型**3. **Crate 的结构**4. **使用 Crate**5. **创建和管理 Crate**6. **发布 Crate**7. **Crate 的优势**8. **示例**创建一个 library crate 二、单元…...

bat 批处理获取日期、时间
在Windows批处理脚本编程中,获取当前日期和时间是一项常见且重要的操作。 1. 获取当前日期和时间的基本脚本 echo off for /F "tokens2" %%i in (date /t) do set mydate%%i set mytime%time% echo Current time is %mydate%:%mytime%输出示例ÿ…...
)
手写tomcat:基本功能实现(3)
TomcatRoute类 TomcatRoute类是Servlet容器,是Tomcat中最核心的部分,其本身是一个HashMap,其功能为:将路径和对象写入Servlet容器中。 package com.qcby.config;import com.qcby.Util.SearchClassUtil; import com.qcby.servlet…...
