LeetCode 39. 组合总和 LeetCode 40.组合总和II LeetCode 131.分割回文串
LeetCode 39. 组合总和
需要注意的是题目已经明确了数组内的元素不重复(重复的话需要执行去重操作),且元素都为正整数(如果存在0,则会出现死循环)。
思路1:暴力解法 + 对最后结果进行去重
- 每一层的遍历都是遍历整个数组,深度遍历也是遍历该数组

Code
class Solution(object):def combinationSum(self, candidates, target):""":type candidates: List[int]:type target: int:rtype: List[List[int]]"""### candidates:即进行横向遍历,又进行深度遍历self.result = []self.path = []self.sum = 0if target < 2:return self.resultsorted_candidates = sorted(candidates)self.backtracking(sorted_candidates, target)#return self.result### 根据输出结果进行去重操作实现的denums = set() final_result = []for sub_array in self.result:sorted_sub_array = sorted(sub_array)denums_tuple = tuple(sorted_sub_array)if denums_tuple not in denums:denums.add(denums_tuple)final_result.append(sub_array)return final_result #### 如何对输出组合进行去重? 又或者如何在回溯的过程中进行去重def backtracking(self, candidates, target):if self.sum == target: ### 终止条件 self.result.append(list(self.path))return if self.sum > target:return for i in range(len(candidates)): ### 横向遍历self.path.append(candidates[i])self.sum += candidates[i]self.backtracking(candidates, target) ### 深度遍历self.sum -= candidates[i]self.path.pop() ### 回溯 思路2:对组合出现一样的问题进行优化

思路1为什么会出现重复的组合,因为比如说从第一层到第二层,你第一个节点是选取了2,然后后续2是不是会选取3,那这样就构成了组合[2,3],你如果你第二个节点从3开始还要去从2开始获取,那你就得到了组合[3,2],这样的话[2,3]和[3,2]就重复了,因此某个处理节点时,下一层的处理节点需要从当前元素开始到后续所有节点,而不再去判断之前的节点了,这样的话就重复判断了。
Code
class Solution(object):def combinationSum(self, candidates, target):""":type candidates: List[int]:type target: int:rtype: List[List[int]]"""### candidates:即进行横向遍历,又进行深度遍历self.result = []self.path = []self.sum = 0if target < 2:return self.resultsorted_candidates = sorted(candidates)self.backtracking(0, sorted_candidates, target)return self.resultdef backtracking(self, start_index, candidates, target):if self.sum == target: ### 终止条件 self.result.append(list(self.path))return if self.sum > target:return for _ in range(start_index, len(candidates)): ### 横向遍历self.path.append(candidates[start_index])self.sum += candidates[start_index]self.backtracking(start_index, candidates, target) ### 深度遍历self.sum -= candidates[start_index]self.path.pop() ### 回溯 start_index += 1继续优化,对思路2进行剪枝操作。思路是先对数组进行排序,将self.sum的值进行判断,如果其大于target了,后续的元素就不用进行深度遍历了。比如说一个数组为[2,3,5,7,8],目标target是6,当已遍历组合为[2,3]时,此时[2,3] 再判断把3放进来后是否等于target,但当前2+3+3=8 > target,因此是不成立的,原本的是执行完对3这个元素遍历完后,通过判断self.sum和target的值来退出,并且后续还会再去判断[2,3]跟7,8结合时的情况,但如果数组是有序,你现在就已经知道当前[2,3]跟3结合后已经大于target,那当前3之后的元素就可以不用进行遍历,因为继续遍历的话也是大于target。
Code
class Solution(object):def combinationSum(self, candidates, target):""":type candidates: List[int]:type target: int:rtype: List[List[int]]"""### candidates:即进行横向遍历,又进行深度遍历self.result = []self.path = []self.sum = 0if target < 2:return self.resultsorted_candidates = sorted(candidates)self.backtracking(0, sorted_candidates, target)return self.resultdef backtracking(self, start_index, candidates, target):if self.sum == target: ### 终止条件 self.result.append(list(self.path))return if self.sum > target:return for _ in range(start_index, len(candidates)): ### 横向遍历if self.sum + candidates[start_index] > target: ### 剪枝breakself.path.append(candidates[start_index])self.sum += candidates[start_index]self.backtracking(start_index, candidates, target) ### 深度遍历self.sum -= candidates[start_index]self.path.pop() ### 回溯 start_index += 1LeetCode 40.组合总和II
思路:
- 每个元素只能使用一次,那递归的start_index 就从 start_index + 1 开始即可满足要求。
- 难点在于如何进行树层的去重,即横向存在相同的元素的话,后续相同元素不需要进行深度遍历,因为遍历结果都已经全部被前面第一个元素给遍历过了。
- 那树层如何进行去重呢?可以将数组的去重思想拿过来,但这样的话会存在问题,每个元素只能使用一次不代表不能使用相同的元素,这意味着我在竖向深度遍历的过程中是可以前一个元素和当前元素相同的。因此,如何进行树层的遍历,需要基于一个used数组来进行优化,这个数组与输入数组长度一致,其为布尔类型,当某个位置的元素正在被使用时,其在used中相同索引下标的值为True。
-
used[start_index-1] == False是为了明确当前不是树枝方向上的去重,当前使用的元素跟上一个元素是相等的可以是竖向遍历的情况,而如果上一个元素目前没被使用,而我当前元素的值却跟上一个元素的值一样,那就证明了是在同一层上。

Code:
class Solution(object):def combinationSum2(self, candidates, target):""":type candidates: List[int]:type target: int:rtype: List[List[int]]"""### 对数组进行排序,继续按照“组合总和”的思路进行解决.### 并且每个元素只能使用一次###但需要执行去重操作,如果当前处理元素跟上一个元素相同的话,则需要跳过当前元素操作,去执行下一个元素。self.result = []self.path = []self.sum = 0used = [False] * len(candidates) ### used的作用是为了进行树层的去重。在同一层上used为True是数量一定是相等的,不同层之间used为True的数量一定不等,下一层总是比上一层多一个sorted_candidates = sorted(candidates)self.backtracking(sorted_candidates, target, 0, used)return self.resultdef backtracking(self, candidates, target, start_index, used):if self.sum == target: ### 终止条件self.result.append(list(self.path)) return if self.sum > target:return for _ in range(start_index, len(candidates)): ## 横向遍历if self.sum + candidates[start_index] > target: ## 剪枝breakif start_index > 0 and candidates[start_index] == candidates[start_index-1] and used[start_index-1] == False: ### 去重. 如何设计去重只是针对当前横向的遍历而不包含竖向的遍历。(本题的关键也是本题的难点)### 首先,candidates[start_index] == candidates[start_index-1]只是说明了我当前使用的元素跟上一个元素是相等的,符合每个元素只使用一次。### used[start_index-1] == False是为了明确当前不是树枝方向上的去重,当前使用的元素跟上一个元素是相等的可以是竖向遍历的情况start_index += 1 ## 执行下个元素的操作continue used[start_index] = True ### 修改used数组,表示我当前used start_index位置的元素是正在使用的self.path.append(candidates[start_index])self.sum += candidates[start_index]self.backtracking(candidates, target, start_index+1, used) ### 每个数字在每个组合中只能使用 一次 self.path.pop()self.sum -= candidates[start_index]used[start_index] = False ### 使用完元素后,进行回溯start_index += 1LeetCode 131.分割回文串
相关文章:

LeetCode 39. 组合总和 LeetCode 40.组合总和II LeetCode 131.分割回文串
LeetCode 39. 组合总和 需要注意的是题目已经明确了数组内的元素不重复(重复的话需要执行去重操作),且元素都为正整数(如果存在0,则会出现死循环)。 思路1:暴力解法 对最后结果进行去重 每一…...

如何在 Windows 11 或 10 上安装 Fliqlo 时钟屏保
了解如何在 Windows 11 或 10 上安装 Fliqlo,为您的 PC 或笔记本电脑屏幕添加一个翻转时钟屏保以显示时间。 Fliqlo 是一款适用于 Windows 和 macOS 平台的免费时钟屏保。它也适用于移动设备,但仅限于 iPhone 和 iPad。Fliqlo 的主要功能是在用户不活动时在 PC 或笔记本电脑…...
)
Linux云计算训练营笔记day08(MySQL数据库)
Linux云计算训练营笔记day08(MySQL数据库) 目录 Linux云计算训练营笔记day08(MySQL数据库)数据准备修改更新update删除delete数据类型1.整数类型2.浮点数类型(小数)3.字符类型4.日期5.枚举: 表头的值必须在列举的值里选择拷贝表复…...
)
计算机视觉与深度学习 | matlab实现EMD-CNN-LSTM时间序列预测(完整源码、数据、公式)
EMD-CNN-LSTM 一、完整代码实现二、核心公式说明1. **经验模态分解(EMD)**2. **1D卷积运算**3. **LSTM门控机制**4. **损失函数**三、代码结构解析四、关键参数说明五、性能优化建议六、典型输出示例以下是用MATLAB实现EMD-CNN-LSTM时间序列预测的完整方案,包含数据生成、经…...

【vue】【环境配置】项目无法npm run serve,显示node版本过低
解决方案:安装高版本node,并且启用高版本node 步骤: 1、查看当前版本 node -v2、配置nvm下载镜像源 1)查看配置文件位置 npm root2)找到settings.txt文件 修改镜像源为: node_mirror: https://npmmirro…...

国芯思辰| 轮速传感器AH741对标TLE7471应用于汽车车轮速度感应
在汽车应用中,轮速传感器可用于车轮速度感应,为 ABS、ESC 等安全系统提供精确的轮速信息,帮助这些系统更好地发挥作用,在紧急制动或车辆出现不稳定状态时,及时调整车轮的制动力或动力分配。 国芯思辰两线制差分式轮速…...

鸿蒙PC操作系统:从Linux到自研微内核的蜕变
鸿蒙PC操作系统是否基于Linux内核,需要结合其技术架构、发展阶段和官方声明综合分析。以下从多个角度展开论述: 一、鸿蒙操作系统的多内核架构设计 多内核混合架构 根据资料,鸿蒙操作系统(HarmonyOS)采用分层多内核架构,内核层包含Linux内核、LiteOS-m内核、LiteOS-a内核…...

小程序弹出层/抽屉封装 (抖音小程序)
最近忙于开发抖音小程序,最想吐槽的就是,既没有适配的UI框架,百度上还找不到关于抖音小程序的案列,我真的很裂开啊,于是我通过大模型封装了一套代码 效果如下 介绍 可以看到 这个弹出层是支持关闭和标题显示的…...

深入理解动态规划:从斐波那契数列到最优子结构
引言 动态规划(Dynamic Programming, DP)是算法设计中一种非常重要的思想,广泛应用于解决各类优化问题。许多看似复杂的问题,通过动态规划的视角分析,往往能找到高效的解决方案。本文将系统介绍动态规划的核心概念,通过经典案例展…...

基于Linux环境实现Oracle goldengate远程抽取MySQL同步数据到MySQL
基于Linux环境实现Oracle goldengate远程抽取MySQL同步数据到MySQL 场景说明: 先有项目需要读取生产库数据,但是不能直接读取生产库数据,需要把生产数据同步到一个中间库,下游系统从中间库读取数据。 生产库mysql - OGG - 中间库…...

电子电路原理第十六章(负反馈)
1927年8月,年轻的工程师哈罗德布莱克(Harold Black)从纽约斯塔顿岛坐渡轮去上班。为了打发时间,他粗略写下了关于一个新想法的几个方程式。后来又经过反复修改, 布莱克提交了这个创意的专利申请。起初这个全新的创意被认为像“永动机”一样愚蠢可笑,专利申请也遭到拒绝。但…...

Go语言数组的定义与操作 - 《Go语言实战指南》
在 Go 语言中,数组(Array) 是一种定长、同类型的集合。它在内存中是连续分布的,适合用于性能敏感的场景。 一、数组的定义 数组的基本语法如下: var 数组名 [长度]元素类型 示例: var nums [5]int …...

物联网简介:万物互联的未来图景
物联网简介:万物互联的未来图景 引言 在科技飞速发展的今天,我们身边的一切似乎都在悄然发生变化。从清晨智能闹钟根据你的睡眠状态自动唤醒,到厨房里的咖啡机在你起床前已经煮好咖啡;从城市交通系统通过实时数据优化红绿灯时长…...

命令拼接符
Linux多命令顺序执行符号需要记住5个 【|】【||】【 ;】 【&】 【&&】 ,在命令执行里面,如果服务器疏忽大意没做限制,黑客通过高命令拼接符,可以输入很多非法的操作。 ailx10 网络安全优秀回答者 互联网…...

【通用智能体】Lynx :一款基于终端的纯文本网页浏览器
Lynx :一款基于终端的纯文本网页浏览器 一、Lynx简介二、应用场景及案例场景 1:服务器端网页内容快速查看场景 2:网页内容快速提取场景 3:表单提交与自动化交互场景 4:网络诊断与调试场景 5:辅助工具适配 三…...

51单片机的lcd12864驱动程序
#include <reg51.h> #include <intrins.h>#define uchar...

GStreamer (三)常⽤插件
常⽤插件 1、Source1.1、filesrc1.2. videotestsrc1.3. v4l2src1.4. rtspsrc和rtspclientsink 2、 Sink2.1. filesink2.2. fakesink2.3. xvimagesink2.4. kmssink2.5. waylandsink2.6. rkximagesink2.7. fpsdisplaysink 3 、视频推流/拉流3.1. 本地推流/拉流3.1.1 USB摄像头3.1…...

Java POJO接收前端null值设置
在 Java 中,若要让 price 字段接收前端传递的 null 值,只需确保以下几点: 1. 使用包装类型 Double 你的 price 字段已经是包装类型 Double(而不是基本类型 double),这天然支持 null 值。基本类型 double …...

详细总结和讲解redis的基本命令
Redis 是一个开源的内存数据结构存储系统,它可以用作数据库、缓存和消息中间件。Redis 支持多种类型的数据结构,如字符串(Strings)、哈希(Hashes)、列表(Lists)、集合(Se…...

Linux 内核等待机制详解:prepare_to_wait_exclusive 与 TASK_INTERRUPTIBLE
1. prepare_to_wait_exclusive 函数解析 1.1 核心作用 prepare_to_wait_exclusive 是 Linux 内核中用于将进程以独占方式加入等待队列的关键函数,其主要功能包括: 标记独占等待:通过设置 WQ_FLAG_EXCLUSIVE 标志,表明此等待条目是独占的。 安全入队:在自旋锁保护下,将条…...

蓝桥杯2300 质数拆分
问题描述 将 2022 拆分成不同的质数的和,请问最多拆分成几个? 01背包问题 #include<iostream> #include<cmath> #include<algorithm> using namespace std;int prime[2025]; int dp[2025]; //dp[j]:和为 j 时的最多拆分…...

软件架构风格系列(2):面向对象架构
文章目录 引言一、什么是面向对象架构风格1. 定义与核心概念2. 优点与局限性二、业务建模:用对象映射现实世界(一)核心实体抽象1. 员工体系2. 菜品体系 (二)封装:隐藏实现细节 三、继承实战:构建…...

ngx_http_random_index_module 模块概述
一、使用场景 随机内容分发 当同一目录下存放多份等价内容(如多张轮播图、不同版本静态页面等)时,可通过随机索引实现负载均衡或流量分散。A/B 测试 通过目录请求自动随机分配用户到不同测试组,无需后端逻辑参与。动态“首页”选…...

go-zero(十八)结合Elasticsearch实现高效数据检索
go-zero结合Elasticsearch实现高效数据检索 1. Elasticsearch简单介绍 Elasticsearch(简称 ES) 是一个基于 Lucene 库 构建的 分布式、开源、实时搜索与分析引擎,采用 Apache 2.0 协议。它支持水平扩展,能高效处理大规模数据的存…...
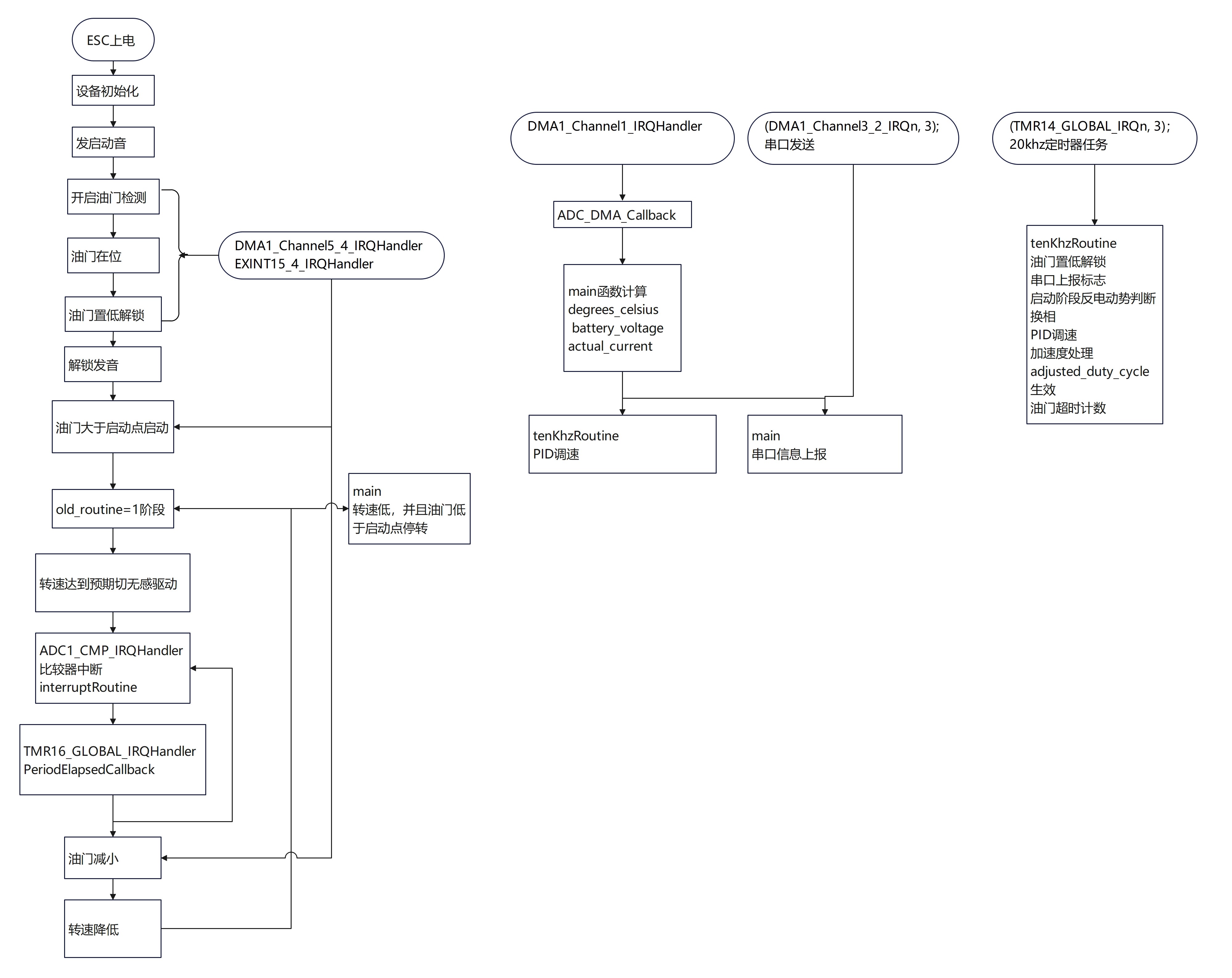
AM32电调学习解读九:ESC上电启动关闭全流程波形分析
这是第九篇,前面的文章把各个模块的实现都介绍了一轮,本章是从运行的角度结合波形图,把整个流程走一遍。 先看下一运行的配置,我把一些配置关闭了,这样跑起来会好分析一些,不同配置跑起来效果会有差异。使用…...

怎么打包发布到npm?——从零到一的详细指南
怎么打包发布到npm?——从零到一的详细指南 目录 怎么打包发布到npm?——从零到一的详细指南一、准备工作1. 注册 npm 账号2. 安装 Node.js 和 npm 二、初始化项目三、编写你的代码四、配置 package.json五、打包你的项目六、登录 npm七、发布到 npm八、…...

NX二次开发C#---遍历当前工作部件实体并设置颜色
该代码片段展示了如何在Siemens NX软件中使用C#进行自动化操作。通过NXOpen和UFSession API,代码首先获取当前工作部件,并遍历其中的所有实体。对于每个实体,代码检查其类型和子类型是否为“实体”,如果是,则将其颜色设…...

如何用体育数据做分析:从基础统计到AI驱动的决策科学
一、体育数据分析的演进与价值创造 体育数据分析已从简单的比分记录发展为融合统计学、计算机科学和运动科学的交叉学科。现代体育组织通过数据分析可以实现: 竞技表现提升:勇士队利用投篮热图优化战术布置 商业价值挖掘:曼联通过球迷行为数…...

09、底层注解-@Import导入组件
09、底层注解-Import导入组件 Import是Spring框架中的一个注解,用于将组件导入到Spring的应用上下文中。以下是Import注解的详细介绍: #### 基本用法 - **导入配置类** java Configuration public class MainConfig { // 配置内容 } Configuration Impo…...

【notes】VScode 使用总结
文章目录 扩展 c/cwindows7 系统下 c/c 自动升级导致的插件无法正常使用 设置 文件格式设置打开文件的默认格式 扩展 c/c windows7 系统下 c/c 自动升级导致的插件无法正常使用 问题 1. c/c扩展的1.25.x版本不再支持windows7 系统,当设置VScode自动升级拓展插件时…...
