我爱学算法之—— 二分查找(中)
一、搜索插入位置
题目解析

这道题,给定一个数组
nums和一个目标值target,让我们在数组nums中找到目标值;如果目标值存在就返回它的下标,如果不存在就返回数target被顺序插入的位置下标。
算法思路
这道题,我们可以使用暴力查找,时间复杂度是O(n)。
从左到右遍历数组,找到值大于等于
target的起始位置(如果target不存在,那要找的就是target顺序插入的位置)
题目要求我们要使用时间复杂度为O(log n)的算法来解决,暴力解法的时间复杂度为O(n)(暴力解法虽然可以通过这道题)
思考以下:数组nums是有序的,且我们要找的是>=target的起始位置,那也就是大于等于target区间的左端点;
我们再随机挑选一个位置i,区间[0,i-1]中的数都是小于i位置的数;区间[i+1 , n]中的数都是大于i位置的数的。
那我们就可以使用二分查找
首先定义
left和right指向数组的起始位置和结束位置。取
mid = left + (right - left)/2比较
mid位置的值和target如果
nums[mid] > target,就去左边区间查找;right = mid - 1。如果
nums[mid] < target,就去右边区间查找;left = mid + 1。如果
nums[mid] == target,就查找到了target,就返回当前位置下标即可。这里因为我们要查找的是
>=target区间的左端点,所以在遍历结束后,l指向的就是target顺序排序的插入位置。
代码实现
class Solution {
public:int searchInsert(vector<int>& nums, int target) {int l = 0, r = nums.size()-1;while(l <= r){int mid = (l + r)/2;if(nums[mid] < target)l = mid + 1;else if(nums[mid] > target)r = mid - 1;elsereturn mid;}return l;}
};
二、x 的平方根
题目解析

这道题,给定一个非负整数
x,然我们计算它的算数平方根。注意:我们返回类型是一个整数,结果只保留整数部分,小数部分要舍去(也就是向下取整)
算法思路
对于这道题,暴力解法:
我们从
0开始向后遍历,依次判断i是不是我们要找的x是算术平方根;这里可以从
x开始向后遍历,查找到第一个i的平方小于等于x的位置。
暴力力解法遍历的区间是[1 , x],我们遍历过程中要判断i的平方是否等于x(或者大于)
但是我们思考一下[1 , x]区间内数的平方它是递增的;
当我们遍历一个位置i时,那[1, i-1]区间内任意一个数的平方都小于i的平方;区间[i+1 , x]内的任意一个数的平方都是大于i的平方的。
所以我们就可以使用二分查找来查找平方<=x区间的左端点。
首先定义
left,right(初始值为0和x),然后取mid = left +(right - left + 1)/2
- 如果
mid*mid<x:此时左边区间数的平方都是小于x,肯定不会是最终结果;left = mid。- 如果
mid*mid>x:此时右边区间数的平方都是大于x,mid平方也是大于x的,肯定也不会是最终结果;right = mid - 1。- 如果
mid*mid==x:此时就找到了x的算数平方根,返回结果即可。最后遍历结束
left和right指向位置就是最终结果。

暴力解法遍历的区间是[1 , x],我们遍历过程中要判断i的平方是否等于x(或者大于)
代码实现
class Solution {
public:int mySqrt(int x) {long long left = 0,right = x;while(left < right){long long mid = left + (right - left + 1)/2;long long sum = mid * mid;if(sum > x)right = mid - 1;else if(sum < x)left = mid;elsereturn mid;}return left;}
};
三、山脉数组的峰顶索引
题目解析

对于这道题,给定一个数组
nums,数组中的数据大小是山峰形状的(也就是先递增,然后再递减)现在我们要找到,山峰峰顶的索引值;也就是先递增再下降的转折点。
算法思路
暴力解法:
遍历数组,找到呈下降趋势的起始位置。
简单来说就是遍历数组,如果当前位置是小于下一个位置的值,也就是下降趋势就继续遍历;
如果当前位置是大于下一个位置的值的,也就是上升趋势就返回结果即可。
题目中说,数组中的值是先递增到一个值再递减的,那也就是说我们遍历一个位置i时,只存在以下两种情况:
- 递增:
nums[i] > nums[i+1] - 递减:
nums[i] < nums[i+1]
所以我们遍历一个位置
i时:
- 如果当前是递增趋势(
nums[i] < nums[i+1]),那区间[l,i]就是递减的,我们要找的最终结果肯定是在区间[i+1, r]中的;- 如果当前是递减趋势,也就是
nums[i] > nums[i+1],那区间[i+1, r]就是递减的,而i位置也可能是我们最终要找的结果,所以我们要找的最终结果肯定是在区间[l,i]中的。所以这道题我们就可以使用二分查找来搜索山峰的峰顶位置。
二分查找
这里我们通过上面分析我们可以发现,我们可以将区间分成两部分,一部分是不满足条件的,一部分可能满足条件的;
而这里我们要找的是递减区间的左端点。
首先定义
left,right(初始值为0和n-1),然后取mid = left +(right - left)/2
- 如果
nums[mid] < nums[mid+1]:此时区间[left , mid]是不满足条件的,就要去区间[mid+1 , right]中查找最终结果。- 如果
nums[mid] > nums[mid+1]:此时区间[mid+1 , right]是不满足条件的,就要去区间[left , mid]中查找最终结果。最后遍历结束,
left和right指向的就是最终结果。
代码实现
class Solution {
public: int peakIndexInMountainArray(vector<int>& arr) {int l = 0, r = arr.size()-1;while(l < r){int mid = (l + r)/2;if(arr[mid] > arr[mid+1])r = mid;elsel = mid+1;}return l;}
};
到这里本篇文章内容就结束了,感谢各位大佬的支持
相关文章:

我爱学算法之—— 二分查找(中)
一、搜索插入位置 题目解析 这道题,给定一个数组nums和一个目标值target,让我们在数组nums中找到目标值;如果目标值存在就返回它的下标,如果不存在就返回数target被顺序插入的位置下标。 算法思路 这道题,我们可以使…...

Golang 并发小结
并发问题概览 问题类型描述数据竞争多个协程对共享变量进行非同步读写操作死锁多个协程互相等待对方释放资源活锁协程不断尝试获取资源但始终失败协程泄漏协程未能及时退出,程序中 goroutine 数量飙升Channel 误用通道未关闭、重复关闭、关闭后写入等问题调度抖动非…...

RTC技术
什么是RTC RTC(Real time communication)实时通信,是实时音视频的一个简称,我们常说的RTC技术一般指的是WebRTC技术,已经被 W3C 和 IETF 发布为正式标准。由于几乎所有主流浏览器都支持 WebRTC 标准 API ,…...

基于Matlab建立不同信道模型
在MATLAB中建立不同的信道模型是无线通信系统仿真的重要组成部分。信道模型用于模拟信号在传输过程中受到的各种影响,如衰减、多径效应、噪声等。以下是一些常见的信道模型及其在MATLAB中的实现方法: 1. 理想信道模型 理想信道假设信号在传输过程中不受…...

uni-app 排坑
记录代码中遇到的一些问题的解决方案 目录 1.自定义弹框 点击弹框以外地方关闭弹框 2.拦截uni-app的tabbar跳转 1.自定义弹框 点击弹框以外地方关闭弹框 1.声明一个变量 const isDialog ref(false) 2.在根容器里面声明一个蒙版 <view class"network-list-wrapper&q…...

军事目标系列之迷彩作战人员检测数据集VOC+YOLO格式2755张1类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):2755 标注数量(xml文件个数):2755 标注数量(txt文件个数):2755 …...

Qt C++实现马的遍历问题
在这个项目中,我们面对的是一个基于中国象棋的马的遍历问题,使用了C++编程语言,并结合了Qt5库来实现图形界面和棋盘的绘制。以下是这个项目涉及的关键知识点: 马的移动规则:马在象棋中具有独特的“日”字形移动方式,即每次可以向前、后、左或右移动一格,然后在同一行或同…...
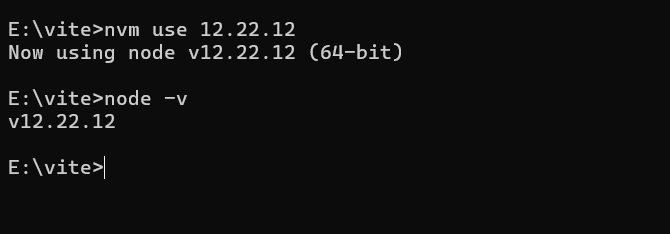
node12.22.12在nvm中安装
1、安装nvm 官网:https://nvm.uihtm.com/ 下载,安装 nvm -v 1.2.22、通过 nvm install 12.22.12 安装报错,找不到此版本 通过下载 https://nodejs.org/zh-cn/downloadzip文件 解压 3、查看nvm 安装路径 nvm root4、在目录下新建文件夹 v…...

技术篇-2.3.Golang应用场景及开发工具安装
Golang 虽然语法简洁,上手也较快,但其在高并发、微服务和云原生领域的优势明显,要真正精通并灵活运用仍需积累大量实践经验。与 Java 借助重量级框架不同,Go 倾向于使用标准库和轻量级第三方包来构建高性能、低延迟的系统。 1.1应…...

高效缓存设计的哲学
文章目录 引言基于缓存存储运算结果锁分段散列减小锁粒度异步化提升处理效率原子化避免重复运算小结参考 引言 基于缓存存储运算结果 利用缓存避免非必要的计算,提升结果获取速度,但还是存在问题,每个线程都需要等待锁才能看结果和运算&…...

【生态信息】开源软件全方位解析
开源软件(0pen Source Software,0ss)是指其源代码可以公开发布、查看、使用和修改的软件。这一概念的核心在于开放性和共享性,允许开发者自由地使用、修改、分发以及改进软件。开源软件通常遵循特定的开源许可证,这些许可证确保了软件的自由使…...

FastAPI在 Nginx 和 Docker 环境中的部署
目录 实现示例1. 项目结构2. FastAPI 应用 (app/main.py)3. 依赖文件 (app/requirements.txt)4. Dockerfile5. Nginx 配置 (nginx/nginx.conf)6. Docker Compose 配置 (docker-compose.yml) 使用方法修改代码后更新 实现示例 接下来创建一个简单的示例项目,展示如何…...

计算机网络相关面试题
一、HTTP1.1和HTTP2的区别 HTTP/1(主要指 HTTP/1.1)和 HTTP/2 是 Web 协议发展中的两个重要版本,二者在性能、协议机制和功能特性上有显著差异。以下从多个维度对比分析,并结合具体案例说明: 一、连接与请求处理方式 1…...

根据当前日期计算并选取上一个月和上一个季度的日期范围,用于日期控件的快捷选取功能
1.选择月份范围 代码如下: <el-date-picker v-model"value" type"monthrange" align"right" unlink-panels range-separator"至"start-placeholder"开始月份" end-placeholder"结束月份" :picker-…...

【C++】set、map 容器的使用
文章目录 1. set 和 multiset 的使用1.1 set类的介绍1.2 set的构造和迭代器1.3 set 的增删查1.4 insert和迭代器调用示例1.5 find和erase使用示例1.6 multiset和set的差异 2. map 和 multimap 的使用2.1 map 类的介绍2.2 pair 类型介绍2.3 map 的构造和迭代器2.4 map 的增删查2…...

【MySQL】第1节|全面理解MySQL架构
快速安装MySQL 使用Docker快速安装mysql8 docker run -d \ --name mysql8 \ --privilegedtrue \ --restartalways \ -p 13306:3306 \ -v /home/mysql8/data:/var/lib/mysql \ -v /home/mysql8/config:/etc/mysql/conf.d \ -v /home/mysql8/logs:/logs \ -e MYSQL_ROOT_PAS…...

YOLOv8模型剪枝笔记(DepGraph和Network Slimming网络瘦身)
文章目录 一、DepGraph剪枝(1)项目准备1)剪枝基础知识2)DepGraph剪枝论文解读12)DepGraph剪枝论文解读23)YOLO目标检测系列发展史4)YOLO网络架构 (2)项目实战(…...

App Builder技术选型指南:从AI编程到小程序容器,外卖App开发实战
在2025年快速迭代的技术生态中,开发者构建App的路径愈发多样化。本文以开发一个同城外卖App为例,对比当前主流的AI编程工具(如Cursor、GitHub Copilot、Trae)与小程序容器技术(如FinClip)的优劣势、难易度及…...

TDengine 高可用——三副本
概述 TDengine 的三副本方案采用 RAFT 算法来实现数据的一致性,包括元数据和时序数据。一个虚拟节点组(VGroup)构成了一个 RAFT 组;VGroup 中的虚拟节点(Vnode),便是该 RAFT 组的成员节点&…...

el-table高度自适应、数据查询后高度展示错误问题
在很多场景中我们需要实现表格的高度自适应,即不同屏幕大小下需要使用不同的高度来设置表格,那么我们应该如何实现呢? 1.el-table实现高度自适应 通过以下代码可以实现表格根据屏幕进行自适应 设置表格的高度 <el-table ref"tableD…...
)
【蓝桥杯真题精讲】第 16 届 Python A 组(省赛)
文章目录 T1 偏蓝 (5/5)T2 IPv6 (0/5)T3 2025 图形 (10/10)T4 最大数字 (10/10)T5 倒水 (15/15)T6 拼好数 (0/15)T7 登山 (20/20)T8 原料采购 (20/20) 更好的阅读体验 高速访问:https://wiki.dwj601.cn/ds-and-algo/lan-qiao-cup/16th-python-a/永久链接࿱…...

Java接口设计:ECharts热力图的绘制
引言 热力图是一种强大的数据可视化工具,通过颜色的深浅变化来直观展示数据密度和分布情况。在现代Web应用中,ECharts作为一款流行的开源数据可视化库,提供了丰富的图表类型,其中热力图因其直观的视觉效果而被广泛使用。本教程将…...

深入理解 MongoDB 的 _id 和 ObjectId:从原理到实践
在 MongoDB 的世界中,_id 字段和 ObjectId 是每个开发者都必须理解的核心概念。作为 MongoDB 文档的唯一标识符,它们不仅影响着数据库的设计,也直接关系到应用的性能和扩展性。本文将全面剖析 _id 和 ObjectId 的工作原理、实际应用场景以及最…...

C++内存复制
C内存复制 方法1 g_savedPoints.resize(pResult->contourData.contourPointCount);//方法1std::copy(pResult->contourData.pointArray, pResult->contourData.pointArray pResult->contourData.contourPointCount, g_savedPoints.begin());方法2 g_savedPoints.r…...

【notepad++如何设置成中文界面呢?】
“Notepad”是一款非常强大的文本编辑软件,将其界面设置成中文的方法如下: 一、工具/原料: 华为 Matebook 15、Windows 10、Notepad 8.4.6。 二 、具体步骤: 1、找到任意一个文本文件,比如 txt 格式的文…...

当AI遇上科研:北大“科学导航”重塑学术探索全流程
在人工智能技术迅猛发展的当下,一场悄然发生的变革,正在改变我们“做科研”的方式。近日,北京大学科学智能研究院联合深势科技,正式上线一款面向科研人员的一体化AI平台——Science Navigator(科学导航)。这…...

大模型在闭合性胫骨平台骨折诊疗全流程中的应用研究报告
目录 一、引言 1.1 研究背景与目的 1.2 国内外研究现状 1.3 研究方法与创新点 二、大模型预测原理及数据基础 2.1 大模型概述 2.2 数据收集与处理 2.3 模型训练与优化 三、术前预测与方案制定 3.1 骨折类型及损伤程度预测 3.2 手术时机评估 3.3 手术方案制定 3.4 …...

PHP学习笔记(八)
目录 返回值 return的使用 多值返回的替代方案 可变函数 内部(内置)函数 匿名函数 静态匿名函数 返回值 值通过可选参数的返回语句返回 return的使用 函数不能返回多个值,但可以通过返回一个数组来得到类似的效果 函数返回一个引用&am…...

C#中WSDL文件引用问题
工作中碰到一个单点登录的需求,因为这个需求同事别的系统已经做过,我这边只需要把代码迁移过来即可,但是迁移过程中发现引用WSDL文件后,方法报错的问题,各种排查代码之后未解决,最终发现是WSDL文件引用的问…...

Ubuntu 22.04上升级Node.js版本
在Ubuntu 22.04上升级Node.js版本有几种方法,推荐使用NVM(Node Version Manager),因为它可以让你轻松管理多个Node.js版本。 方法1: 使用NVM(推荐) 1. 安装NVM # 下载并安装NVM curl -o- https://raw.gi…...
