高等数学-微分

一、一元函数：

在实际应用中，经常需要近似计算函数y=f(x)的增量Δy=f(x)-f(x0)=f(x0+Δx)-f(x0),其中一种近似称为函数的微分。

定义：若函数y=f(x)在点x0处的增量Δy可表达为自变量增量Δx的线性函数AΔx和Δx的高阶无穷小量之和，即Δy=f(x0+Δx)-f(x0)=AΔx+o(Δx),(Δx->0)

其中，A是不依赖于Δx的某一常数，则称函数y=f(x)在点x0处可微，并记函数y=f(x)在点x0处的微分为dy|x=x0=df|x=x0=AΔx=Adx

定理：函数y=f(x)在点x0处可微的充要条件为函数y=f(x)在点x0处可导，且dy|x=xo=f'(x0)dx

函数可微性的几何意义：函数在某点附近可用其切线近似表示（不是等于，极限也不相等）（当Δx->0，(Δy-dy)/Δx->0)

函数的导数y'=dy/dx可用函数微分dy和自变量微分dx之比表示

（1）为什么可微一定可导？

对于一元函数f(x)，若在x=a处可微，表函数在该点有一个局部线性化的形式，存在一个常数f'(a)，使得在a点附近，函数值的变化可以通过下式近似：f(a+h)~~f(a)+f'(a)h(当h->0时)，也就是说，函数的增量可以通过线性项f'(a)h来近似。f'(a)即是f(x)在x=a处的导数。

（2）为什么可导一定可微？

可微：函数f(x)在某点x=a处可微，意味着函数在该点具有一个明确的局部线性逼近，存在切线。即，函数可以写成：f(a+h)≈f(a)+f′(a)h

更严格地说，如果函数可微，那么存在常数f'(a)，使得：

          f(a+h)-f(a)-f'(a)h

lim   ________________=0

h->0             h

推导过程：

1、根据导数定义，函数在点x=a处可导，意味着：

               f(a+h)-f(a)

f'(a)=lim_______________

       h->0     h

现在要证明函数在点a处是可微，即证明：

      f(a+h)-f(a)-f'(a)h

lim ________________=0

h->0          h

这意味着函数在a点处的增量可以被线性化，剩下的误差项趋于 0。

2、先将增量f(a+h)-f(a)分解成两部分：

f(a+h)-f(a)=f'(a)h+o(h)

其中，o(h)表示高阶无穷小，意味着o(h)相对于h增长得更慢（即o(h)/h→0当h→0时）。【为什么可以这样分？】（资料上说：导数的定义和极限的性质）

3、代入：

f(a+h)-f(a)-f'(a)h              o(h)

________________ = ________

            h                            h

4、由于o(h)是高阶无穷小，满足o(h)/h->0当h->0时，因此：

        o(h)

lim    ___   =0

h->0    h

这就证明了：

       f(a+h)-f(a)-f'(a)h

lim  ________________ =0

h->0       h

从而证明了函数在点a处是可微的。

(3)可导一定连续。连续不一定可导（y=|x|在x=0处不可导）。

证明：由于，f'(x0)存在，所以

f'(x0)=lim*{x->x0} [f(x)-f(x0)]/(x-x0)存在，从而

lim*{x->x0} [f(x)-f(x0)]=lim*{x->x0} [f(x)-f(x0)]/(x-x0) • (x-x0)=0

即 lim*{x->x0} f(x)=f(x0)

所以，f(x)在点x0处连续

二、二元函数

（1）可微必连续（连续必可微？？）

多元函数连续性定义:

设函数f(x,y)在点p。(x。,y。）的某个邻域内有定义，如果limf(x,y)=f(x。，y。），则称函数f(x,y)在点p。处连续。                                                                  x->x。

                                                                                             y->y。 

证明：

根据可微性的定义：

f(a+Δx,b+Δy)−f(a,b)=fx​(a,b)Δx+fy​(a,b)Δy+o(ρ)

其中 o(ρ​) 是比ρ​更小 的高阶无穷小。

两边取极限：

Δx,Δy→0lim​[f(a+Δx,b+Δy)−f(a,b)]=Δx,Δy→0lim​[fx​(a,b)Δx+fy​(a,b)Δy+o(ρ)]

由于Δx,Δy→0时fx(a,b)Δx和 fy(a,b)Δy也趋于 0，而 o(​ρ) 是高阶无穷小，也趋于 0，因此右边极限为 0。

所以我们得到：lim⁡Δx,Δy→0[f(a+Δx,b+Δy)−f(a,b)]=0

这正是函数f(x,y)在(a, b)处连续性的定义：(x,y)->(a,b)lim​f(x,y)=f(a,b)

（2）可微必可导

（3）可导不一定可微，可导不一定连续（连续必可导？？）

                        xy

                      _______

                       x^2+y^2          ,x^2+y^2<>0

例如f(x,y)={

                        0，                x^2+y^2=0

f(x,y)在原点（0,0)处的两个导数：fx(0,0)=Δx->0lim[f(0+Δx,0)-f(0,0)]/Δx=0同理fy(0,0)=0

都存在，但在原点(0，0）处不连续，从而在原点(0，0）处不可微。这是因为：假如函数f(x,y)在原点(0，0）处可微，则它必连续，从而矛盾。

三、偏导数

（1）偏导数的几何意义

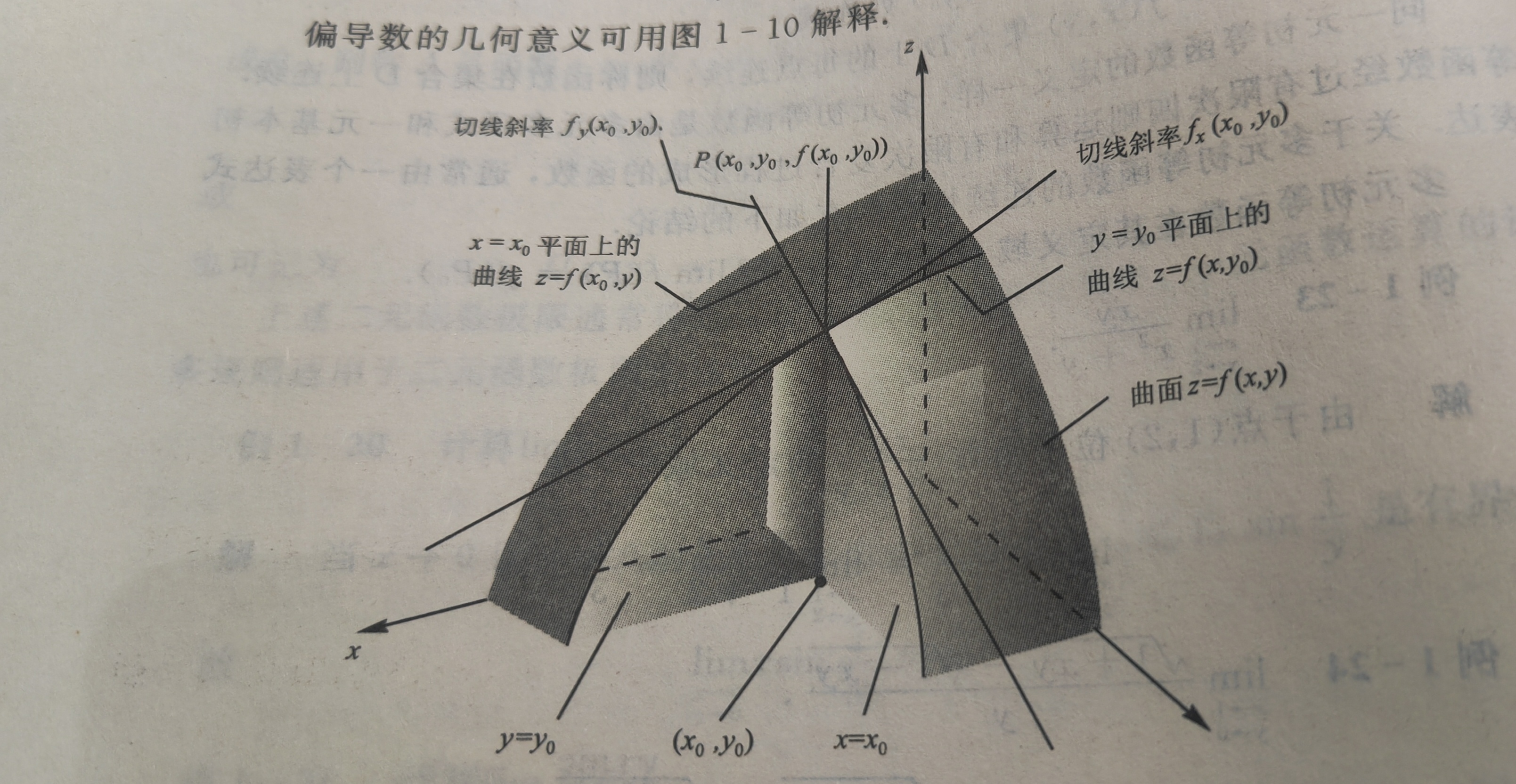
（2）证明：函数z=√(x^2+y^2)在(0,0)处连续，但两个偏导数都不存在。

1）原函数的图像是一个以原点(0,0,0)为顶点的圆锥面。无论从任何方向接近顶点，高度z都会逐渐降低到0，没有跳跃或空洞。这种几何形状表明，函数在原点处是平滑连接的因此连续

2）

(1)当点(x，y)接近于0时，距离公式的值趋近于0。

(2)计算极限值：

lim*(x，y)->(0,0)√(x^2+y^2)=√(0^2+0^2)=0

（3）比较极限值与函数值：

   f(0，0）=0

结论：极限值等于函数值，因此函数在（0，0）处连续

3）

(a)对x的偏导数：

fx(0,0)=lim*h->0(f(h，0)-f(0,0))/h=lim*h->0(

√h^2-0)/h=lim*h->0(|h|/h)

当 h -> 0^+ 时，|h|/h = 1 ；

当 h ->0^- 时,|h|/h} = -1 。

由于左右极限不相等，极限不存在，故fx在(0,0)处极限不存在。

(b)

同理：对y的偏导数fy在(0,0)处也不存在。

（3）复合函数和隐函数的偏导数

(1)F(x)=0对定义域的所有x恒成立，则F'(x)=0(理解：导数是函数值随x的变化率)

(2)应用：单位圆方程x^2+y^2=1确定了一个y(x)的隐函数。

F(x,y)=x^2+y^2-1

dF[x,y(x)]/dx=0 理解：此时看作对x求导，y看作关于x的中间变量

2x+2y*(dy/dx)=0 理解：隐函数求导结果包含y，不用化简

结论1：

隐函数是一元函数

dy/dx=-Fx/Fy

Fx是二元函数对x的偏导，Fy是二元函数对xpy的偏导

结论2：

隐函数是二元函数

∂z/∂x=-Fx/Fz

∂z/∂y=-Fy/Fz

四、偏导数的应用-极值与最值

a.一元函数：

极值含义：1）

函数y=f(x)在点x0的某邻域（x0-Δx,x0+Δx）中有定义，x0是函数在（x0-Δx,x0+Δx）内的最值点

最值：连续函数y=f(x)在区间[a,b]上的最大值（最小值类似）问题时，最大值只能是函数的驻点，不可导点或区间的端点

设函数f(x)在点x0处取到极值，且y=f(x)在点x0处可导，则必有f'(x0)=0

若x0是极值点，则要么f'(x0)=0,要么函数y=f(x)在x0处不可微,驻点不一定是极值点（y=x^3,x=0)

函数的极值点通常出现在驻点或不可导点(??)

设函数y=f(x)在点xo的某邻域（x0-Δx,x0+Δx)上有定义，且x0是y=f(x)的驻点或 y=f(x)在点x0处不可导，则：

如果f'(x0)=0，且f''(x0)<0，则x=x0为函数y=f(x)的极大值点（极小值点类似）？？

b.二元函数的极值与最值:

设f(x0,y0)是函数z=f(x,y)的极值点，且函数z=f(x,y)在点(x0,y0)处偏导数存在，则fx(x0,y0)=0,fy(x0,y0)=0;

类似于一元函数的讨论，同时使得fx(x,y)=0,fy(x,y)=0的点(x0,y0)称为函数z=f(x,y)的驻点（在函数可导的条件下，极值点必为驻点）;

在极值点处函数的所有偏导数必定为0或至少一个偏导数不存在(z=✔️(x^2+y^2))。但驻点却不一定是极值点(z=y^2-x^2)。

五、偏导数的应用—梯度

设z=f(x,y)在平面区域D上有定义，点(x,y)属于D，l是一个向量，记l的方向余弦为(cosa，sina)，即(cosa，sina)=l，其中a为从x轴正向到向量l的转角。

例1:

例2:

六、偏导数的应用—切平面和法平面

1)法平面

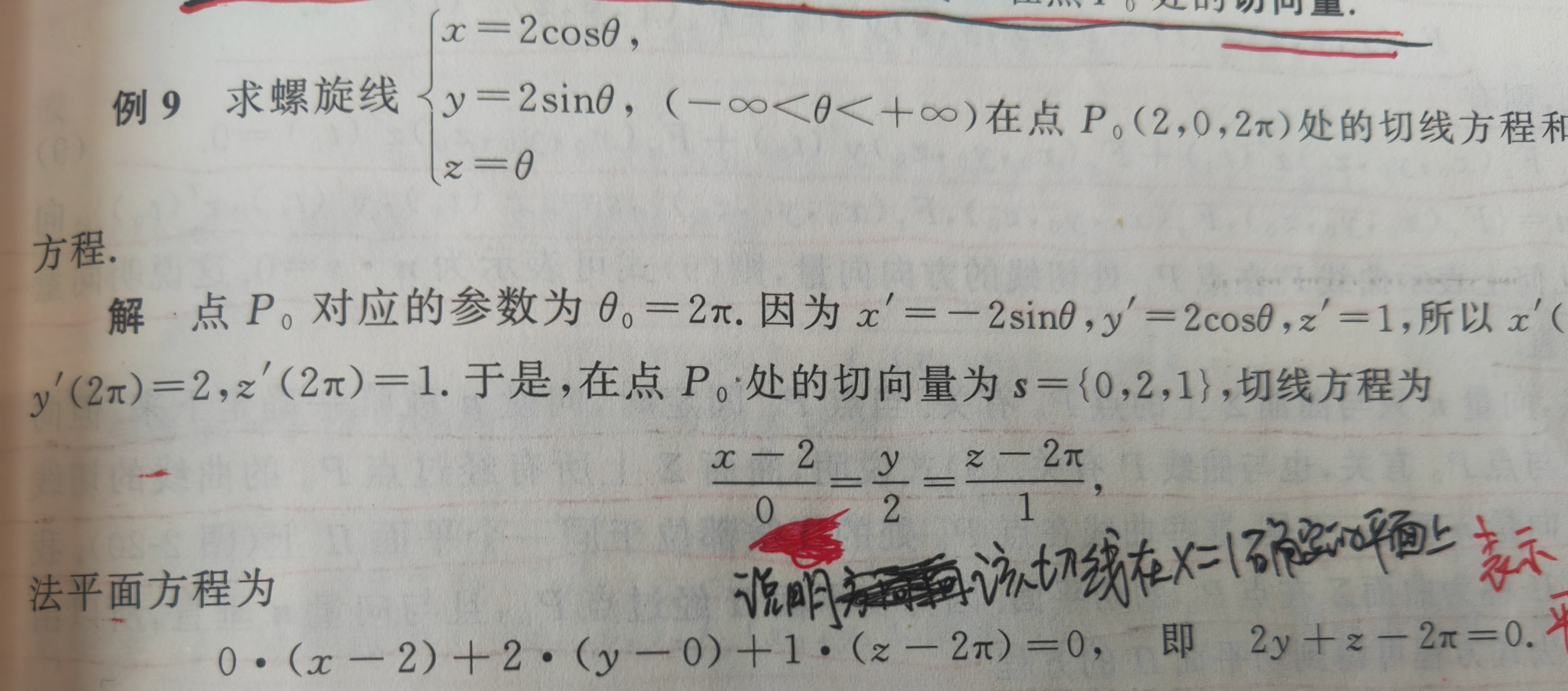
2）切平面

设曲面Σ的一般方程为F(x，y，z)=0，其中F(x，y，z)具有连续的偏导数。设曲面上过点P0(x0,y0,z0)的曲线

  x=x(t)

{ y=y(t)  满足x(t0)=x0,y(t0)=y0,z(t0)=z0。由于曲线在曲面Σ上，则F(x(t),y(t),z(t))=0，对t求导得：

  z=z(t)

Fxx'(t)+Fyy'(t)+Fzz'(t)=0

令t=t0得

Fx(P0)x'(t0)+Fy(P0)y'(t0)+Fz(P0)z'(t0)=0

上式表明向量(Fx(x0,y0,z0),Fy(x0,y0,z0),Fz(x0,y0,z0))垂直于曲面上任意过点P0(x0,y0,z0)处的曲线的切向量，因此(Fx(x0,y0,z0),Fy(x0,y0,z0),Fz(x0,y0,z0))就是曲面在点P0(x0,y0,z0)处的切平面π的法向量，即曲面上点P0(x0,y0,z0)处的法向量n

由此得到曲面上的点P0(x0,y0,z0)处的切平面π方程为Fx(P0)(x-x0)+Fy(P0)(y-y0)+Fx(P0)(z-z0)=0

法线方程：(x-x0)/Fx(P0)=(y-y0)/Fy(P0)=(z-z0)/Fz(P0)

若曲面方程为一般方程：f(x,y)-z=0 法向量为n=(fx(x0,y0),fy(x0,y0),-1)，切平面方程为fx(x0,y0)(x-x0)+fy(x0,y0)(y-y0)-(z-f(x0,y0))=0

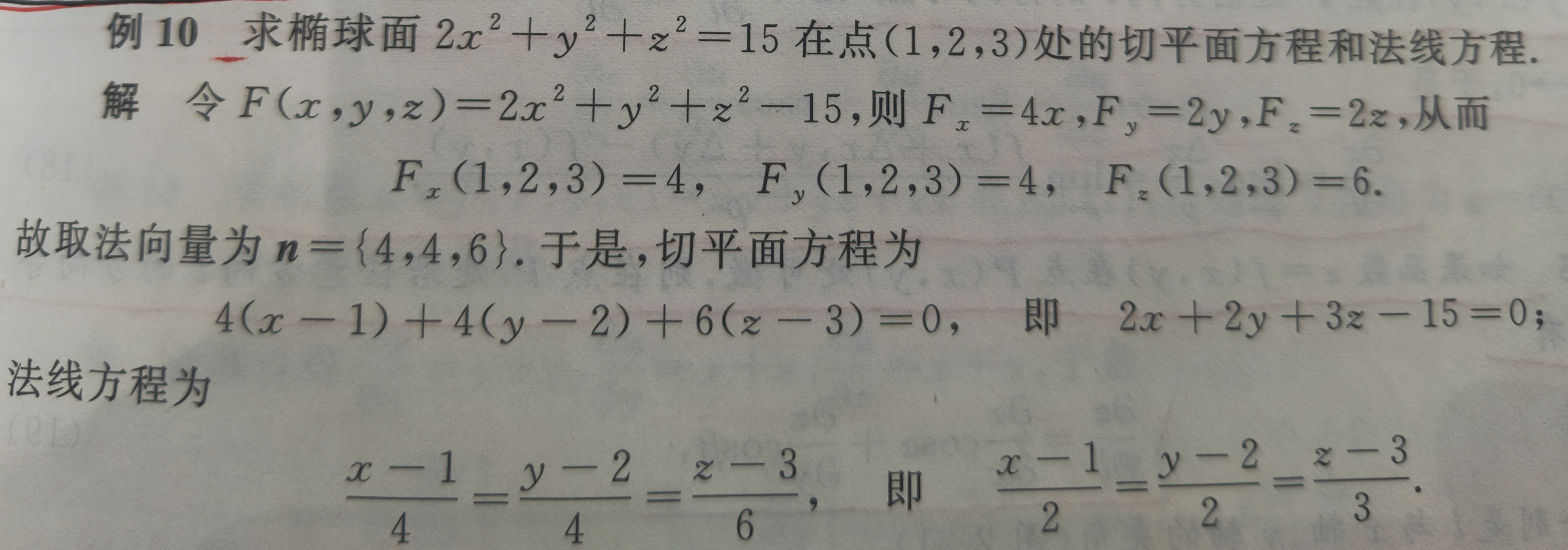
注：(1)曲面上一点的法向量(根据曲面函数的偏导函数计算)只与点的坐标有关，只要点的坐标确定，该法向量就确定，法向量的方向余弦同样只与点的坐标有关，所以曲面上点的法向量的方向余弦是关于x,y（针对曲面由方程z=f(x,y)给出）的二元函数。