每日c/c++题 备战蓝桥杯(修理牛棚 Barn Repair)
修理牛棚 Barn Repair 题解
问题背景与挑战
在一个暴风雨交加的夜晚,Farmer John 的牛棚遭受了严重的破坏。屋顶被掀飞,大门也不翼而飞。幸运的是,许多牛正在度假,牛棚并未住满。然而,为了保护那些还在牛棚里的牛,Farmer John 必须尽快用木板修复牛棚。但是,他的木材供应商是一个吝啬鬼,只能提供有限数量的木板。为了避免浪费资源,Farmer John 希望以最少的木板总长度覆盖所有有牛的牛棚。这是一个典型的优化问题,我们需要在资源有限的情况下,找到最优的解决方案。
输入输出格式详解
输入
输入数据包含两部分:
- 第一行包含三个整数 m、s 和 c,分别表示木板的最大数目、牛棚的总数以及牛的总数。
- 接下来 c 行,每行包含一个整数,表示牛所在的牛棚编号。
输出
输出一个整数,表示覆盖所有有牛的牛棚所需的最小木板总长度。
问题分析与思路探索
这道题是一个典型的区间覆盖问题。我们需要用有限的木板覆盖所有有牛的牛棚,同时使木板的总长度最小。这就好比在一条数轴上,有若干个点(牛棚编号),我们的任务是选择若干个区间(木板的覆盖范围),使这些区间的总长度最短。
我最初的想法是直接暴力枚举所有可能的覆盖方式,但很快意识到这种方法的局限性。随着牛棚数量和木板数量的增加,暴力搜索的时间复杂度呈指数级增长,根本无法在合理的时间内解决问题。于是,我开始思考如何利用动态规划(Dynamic Programming,DP)来优化这个问题。
动态规划是一种将复杂问题分解为简单子问题的算法思想。它通过存储子问题的解,避免重复计算,从而大大提高算法效率。在这个问题中,我们可以定义一个二维数组 f[i][j],表示用 j 块木板覆盖前 i 个牛棚的最小总长度。通过对子问题的逐步求解,我们可以最终得到全局最优解。
动态规划的思路与状态转移方程
动态规划表的定义
我们定义 f[i][j] 表示用 j 块木板覆盖前 i 个牛棚的最小总长度。这是一个二维数组,其中 i 表示牛棚的编号,j 表示使用的木板数量。
状态转移方程的推导
对于每个牛棚 i 和木板数目 j,我们有两种选择:
-
放置新的木板:如果在当前牛棚 i 处放置一块新的木板,那么总长度将增加 1(因为每个牛棚的宽度相同),并且使用的木板数量增加 1。这种情况下,状态转移方程为:
f [ i ] [ j ] = f [ i − 1 ] [ j − 1 ] + 1 f[i][j] = f[i - 1][j - 1] + 1 f[i][j]=f[i−1][j−1]+1 -
延长已有木板:如果选择延长已有木板,那么总长度将增加当前牛棚与前一个牛棚之间的距离,即
pp[i] - pp[i - 1]。这种情况下,状态转移方程为:
f [ i ] [ j ] = f [ i − 1 ] [ j ] + ( p p [ i ] − p p [ i − 1 ] ) f[i][j] = f[i - 1][j] + (pp[i] - pp[i - 1]) f[i][j]=f[i−1][j]+(pp[i]−pp[i−1])
最终,f[i][j] 的值为上述两种情况的较小值:
f [ i ] [ j ] = min ( f [ i − 1 ] [ j − 1 ] + 1 , f [ i − 1 ] [ j ] + ( p p [ i ] − p p [ i − 1 ] ) ) f[i][j] = \min(f[i - 1][j - 1] + 1, f[i - 1][j] + (pp[i] - pp[i - 1])) f[i][j]=min(f[i−1][j−1]+1,f[i−1][j]+(pp[i]−pp[i−1]))
初始化
在动态规划过程中,初始化是非常重要的一步。
-
当没有任何牛棚和木板时,总长度为 0,即:
f [ 0 ] [ 0 ] = 0 f[0][0] = 0 f[0][0]=0 -
对于其他不可达的状态,我们将其初始化为一个很大的值(如
1 << 30),表示这些状态在初始阶段是不可到达的。
代码实现
以下是基于上述思路的完整代码实现:
#include<bits/stdc++.h>
using namespace std;int m, s, c; // 木板的最大数目、牛棚的总数和牛的数量
int f[205][205] = {0}; // 动态规划表
int pp[205] = {0}; // 牛棚编号数组int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin >> m >> s >> c; // 输入木板数、牛棚总数和牛的数量for (int i = 1; i <= c; ++i) {cin >> pp[i]; // 输入牛所在的牛棚编号}sort(pp + 1, pp + c + 1); // 对牛棚编号进行排序// 初始化DP表for (int i = 1; i <= c; ++i) f[i][0] = 1 << 30;for (int i = 1; i <= m; ++i) f[0][i] = 1 << 30;// 填充DP表for (int i = 1; i <= c; ++i) {for (int j = 1; j <= m; ++j) {f[i][j] = min(f[i - 1][j - 1] + 1, f[i - 1][j] + (pp[i] - pp[i - 1]));}}cout << f[c][m] << endl; // 输出结果return 0;
}
测试与验证
我使用题目中的样例输入对代码进行了测试:
输入:
4 50 18
3
4
6
8
14
15
16
17
21
25
26
27
30
31
40
41
42
43
输出结果为 135,与题目中的预期结果一致。这表明代码能够正确处理样例输入,并计算出覆盖所有有牛的牛棚所需的最小木板总长度。
总结与拓展
通过动态规划的方法,我们可以高效地解决修理牛棚的问题。动态规划的核心在于将复杂问题分解为简单子问题,利用状态转移方程逐步构建解决方案。在这个过程中,我们不仅需要仔细设计状态表示,还需要合理推导状态转移方程,以确保算法的正确性和高效性。
这种方法不仅适用于这道题,还可以解决类似的区间覆盖问题。通过不断练习和总结,我们可以更好地掌握动态规划的思想和技巧,提升解决复杂问题的能力。希望这篇题解能够帮助你更好地理解动态规划的应用,以及如何在实际问题中灵活运用它。
相关文章:
)
每日c/c++题 备战蓝桥杯(修理牛棚 Barn Repair)
修理牛棚 Barn Repair 题解 问题背景与挑战 在一个暴风雨交加的夜晚,Farmer John 的牛棚遭受了严重的破坏。屋顶被掀飞,大门也不翼而飞。幸运的是,许多牛正在度假,牛棚并未住满。然而,为了保护那些还在牛棚里的牛&am…...

6个月Python学习计划 Day 3
🎯 今日目标 掌握 while 和 for 循环的使用方式理解 range() 的工作机制实践:打印 1~100、累加、九九乘法表等常见程序逻辑 🧠 学习内容详解 while 循环 i 1 while i < 5:print(f"第 {i} 次循环")i 1📌 特点&…...

Linux虚拟文件系统(2)
2.3 目录项-dentry 目录项,即 dentry,用来记录文件的名字、索引节点指针以及与其他目录项的关联关系。多个关联的目录项,就构成了文件系统的目录结构。和上一章中超级块和索引节点不同,目录项并不是实际存在于磁盘上的,…...

【数据结构】栈和队列(上)
目录 一、栈(先进后出、后进先出的线性表) 1、栈的概念及结构 2、栈的底层结构分析 二、代码实现 1、定义一个栈 2、栈的初始化 3、入栈 3、增容 4、出栈 5、取栈顶 6、销毁栈 一、栈(先进后出、后进先出的线性表) 1、…...

科技赋能·长效治理|无忧树建筑修缮渗漏水长效治理交流会圆满举行!
聚焦行业痛点,共话长效未来!5月16日,由无忧树主办的主题为“科技赋能长效治理”的建筑修缮渗漏水长效治理技术交流会在上海圆满举行。来自全国的建筑企业代表、专家学者、技术精英齐聚一堂,共探渗漏治理前沿技术,见证科…...

【闲聊篇】java好丰富!
1、在学习mybatis-plus的文档时,发现引入了solon依赖,才发现这是一个对标spring生态的框架,有意思! 还有若依框架,真的好丰富~~~~~~~ 2、今天面试官问我,他说很少遇到用redission做延迟队列的。后面我就反…...

STL中list的模拟
这里写目录标题 list 的节点 —— ListNodelist 的 “导览员” —— ListIteratorlist 的核心 —— list 类构造函数迭代器相关操作容量相关操作 结尾 在 C 的 STL(标准模板库)中,list 是一个十分重要的容器,它就像一个灵活的弹簧…...

6.3.2图的深度优先遍历
知识总览: 树的先根遍历: 采用递归一直找某个节点的子树直到找不到从上往下找 访问根节点1,1的子树有2、3、4,访问2,2节点子树有5访问5,5没有子树,退回到2,2还有子树6访问6,6没有子树再退回到2,2的子树都被访问了再退…...

畅游Diffusion数字人(30):情绪化数字人视频生成
畅游Diffusion数字人(0):专栏文章导航 前言:仅从音频生成此类运动极具挑战性,因为它在音频和运动之间存在一对多的相关性。运动视频的情绪是多元化的选择,之前的工作很少考虑情绪化的数字人生成。今天解读一个最新的工作FLOAT,可以生成制定情绪化的数字人视频。 目录 贡献…...

UE5 Va Res发送请求、处理请求、json使用
文章目录 介绍发送一个Get请求发送Post请求设置请求头请求体带添json发送请求完整的发送蓝图 处理收到的数据常用的json处理节点 介绍 UE5 自带的Http插件,插件内自带json解析功能 发送一个Get请求 只能写在事件图表里 发送Post请求 只能写在事件图表里 设置…...
.openEndDrawer();不生效问题)
关于flutter中Scaffold.of(context).openEndDrawer();不生效问题
原因: 在 Flutter 中,Scaffold.of(context) 会沿着当前的 context 向上查找最近的 Scaffold。如果当前的 widget 树层级中没有合适的 Scaffold(比如按钮所在的 context 是在某个子 widget 中),就找不到它。 解决办法…...

【C++】深入理解C++中的函数与运算符重载
文章目录 前言一、什么是重载?1.1 函数重载1.1.1 函数重载的规则1.1.2 示例:函数重载 1.2 运算符重载1.2.1 运算符重载的规则1.2.2 示例:运算符重载 1.2.3 运算符重载的注意事项 二、重载的注意事项2.1 重载的二义性2.2 默认参数和重载2.3 运…...
【读代码】BAGEL:统一多模态理解与生成的模型
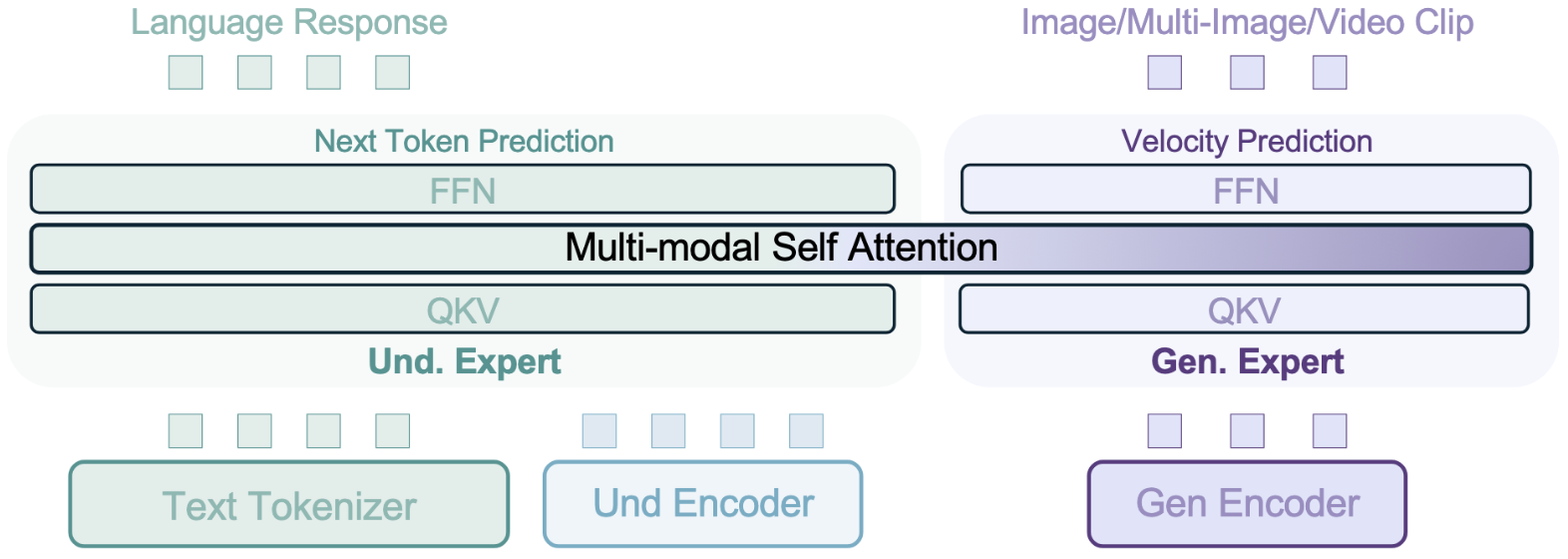
一、项目概览 1.1 核心定位 BAGEL是字节跳动推出的开源多模态基础模型,具有70亿激活参数(140亿总参数)。该模型在统一架构下实现了三大核心能力: 多模态理解:在MME、MMBench等9大评测基准中超越Qwen2.5-VL等主流模型文本生成图像:生成质量媲美SD3等专业生成模型智能图像…...

隧道自动化监测解决方案
行业现状 隧道作为一种重要的交通运输通道,不管是缓解交通压力,还是让路网结构更趋于完善,它都有着不可估量的作用。隧道在运营过程中,由于受到材料退化、地震、人为因素等影响会发生隧道主体结构的损坏和劣化。若不及时检修和维护…...

如何通过EventChannel实现Flutter与原生平台的双向通信?
在Flutter开发中,EventChannel是处理单向数据流的核心组件,尤其适用于原生平台(Android/iOS)主动向Flutter端推送实时数据的场景,例如传感器数据、后台任务通知等。虽然EventChannel本身以原生到Flutter的单向通信为主,但结合特定设计模式,仍可实现双向交互。本文将详细…...

游戏引擎学习第307天:排序组可视化
简短谈谈直播编程的一些好处。 上次结束后,很多人都指出代码中存在一个拼写错误,因此这次我们一开始就知道有一个 bug 等待修复,省去了调试寻找错误的时间。 今天的任务就是修复这个已知 bug,然后继续排查其他潜在的问题。如果短…...

java接口自动化初识
简介 了解什么是接口和为什么要做接口测试。并且知道接口自动化测试应该学习哪些技术以及接口自动化测试的落地过程。 一、什么是接口 在这里我举了一个比较生活化的例子,比如我们有一台笔记本,在笔记本的两端有很多插口。例如:USB插口。那…...

工作流引擎-01-Activiti 是领先的轻量级、以 Java 为中心的开源 BPMN 引擎,支持现实世界的流程自动化需求
前言 大家好,我是老马。 最近想设计一款审批系统,于是了解一下关于流程引擎的知识。 下面是一些的流程引擎相关资料。 工作流引擎系列 工作流引擎-00-流程引擎概览 工作流引擎-01-Activiti 是领先的轻量级、以 Java 为中心的开源 BPMN 引擎&#x…...

时序数据库IoTDB的分片与负载均衡策略深入解析
一、引言 随着数据库服务的业务负载增加,扩展服务资源成为必然需求。扩展方式主要分为纵向扩展和横向扩展。纵向扩展通过增加单台机器的能力(如内存、硬盘、处理器)来实现,但受限于单台机器的硬件能力。而横向扩展则通过增加更多…...

NVM安装使用及问题解决
目录 一、前言 二、NVM安装 三、配置下载源 四、nvm使用 五、安装nvm list available没有的版本 六、问题解决 一、前言 如果你开发 Node.js 项目,可能会遇到这些问题: ①新项目需要 Node.js 18,但老项目只能用 Node.js 14,…...

C++学习之STL学习:string类使用
在之前的学习中,我们初步了解到了STL的概念,接下来我们将深入学习STL中的string类的使用,后续还会结合他们的功能进行模拟实验 目录 为什么要学习string类? 标准库中的string类 string类(了解) auto和范围…...

基于 STC89C52 的养殖场智能温控系统设计与实现
摘要 本文提出一种基于 STC89C52 单片机的养殖场环境温度智能控制系统,通过集成高精度温度传感器、智能执行机构及人机交互模块,实现对养殖环境的实时监测与自动调控。系统具备温度阈值设定、超限报警及多模式控制功能,可有效提升养殖环境稳定性,降低能耗与人工成本。 一…...

redis哨兵服务
配置主机Host67为master服务器配置主机host68为 slave服务器配置主机host69运行哨兵服务测试配置 IP地址主机名192.168.10.167redis167192.168.10.168redis168192.168.10.169redis169 步骤一:配置主机Host67为master服务器 [rootredis169 ~]# vim /etc/redis.c…...

5月24日day35打卡
模型可视化与推理 知识点回顾: 三种不同的模型可视化方法:推荐torchinfo打印summary权重分布可视化进度条功能:手动和自动写法,让打印结果更加美观推理的写法:评估模式 作业:调整模型定义时的超参数&#x…...

嵌入式<style>设计模式
每天分享一个web前端开发技巧。 今天分享的主题是,如何提升前端代码的内聚性。我们在写<style></style>的时候,往往把大量无关联的样式写在同一个<style>下,而且离相关的html元素很远,这样导致每次想修改某个元…...

Kotlin 中该如何安全地处理可空类型?
在 Kotlin 中,可空类型(如 String?)是语言设计的核心特性之一,旨在从编译时避免 NullPointerException(NPE)。 1 核心处理方式 1.1 安全调用操作符(?.) 直接调用可空对象的方法…...

基于大模型预测的视神经脊髓炎技术方案
目录 一、术前评估与预测1. 数据采集与预处理2. 大模型构建与训练3. 术前风险评估与预测二、术中监测与决策支持1. 实时数据采集与传输2. 术中决策支持系统三、术后管理与康复1. 术后早期预警与监测2. 康复效果预测与个性化方案四、并发症风险预测与防控1. 并发症风险预测模型2…...
)
使用防火墙禁止程序联网(这里禁止vscode)
everything搜一下Code.exe的安装路径:D:\downloadApp1\vscode\Microsoft VS Code\Code.exe 方法:使用系统防火墙(推荐) Windows 通过防火墙阻止 VS Code: 打开 Windows Defender 防火墙(控制面板 > 系统…...

Linux(7)——进程(概念篇)
目录 一、基本概念 二、描述进程——PCB 1.task_struct——PCB的一种 2.task_struct的内容分类 三、查看进程 1.通过系统目录查看 2.通过ps命令查看 四、通过系统调用获取进程的PID和PPID 五、通过系统调用创建进程 1.fork函数创建子进程 2.使用if来引出问题 六、L…...

前端流行框架Vue3教程:24.动态组件
24.动态组件 有些场景会需要在两个组件间来回切换,比如 Tab 界面 我们准备好A B两个组件ComponentA ComponentA App.vue代码如下: <script> import ComponentA from "./components/ComponentA.vue" import ComponentB from "./…...
