每日算法 -【Swift 算法】反转整数的陷阱与解法:Swift 中的 32 位整数处理技巧
反转整数的陷阱与解法:Swift 中的 32 位整数处理技巧
在面试题和算法练习中,整数反转是一道非常经典的题目。乍一看很简单,但一旦加入“不能使用 64 位整数”和“不能溢出 32 位整数范围”这两个限制,问题就立刻变得有挑战性。本文将带你深入剖析这道题,并用 Swift 实现一个健壮、符合题意的解决方案。
🧩 题目描述
给定一个 32 位有符号整数 x,请你返回将 x 数字部分反转后 的结果。如果反转后整数超过了 32 位有符号整数的表示范围 [-2³¹, 2³¹ - 1],那么就返回 0。
举个例子:
输入: 123 → 输出: 321
输入: -123 → 输出: -321
输入: 1534236469 → 输出: 0(反转后溢出)
🧠 解题思路
这个问题的难点在于 处理可能的溢出情况,并且不能依赖 64 位整数类型。
思考步骤:
- 每次取出
x的最后一位:pop = x % 10 - 将其添加到结果中:
result = result * 10 + pop - 处理过程中要判断是否即将溢出
关键点:如何判断溢出?
反转之前:
result * 10 + pop
可能会超过 Int32 的范围,所以我们必须在计算之前判断是否 即将溢出:
if result > Int32.max / 10 || (result == Int32.max / 10 && pop > 7) {return 0
}
负数同理。
💻 Swift 实现(含详细中文注释)
func reverse(_ x: Int) -> Int {// 定义 32 位整数的最大值和最小值let INT_MAX = Int32.max // 2147483647let INT_MIN = Int32.min // -2147483648var x = x // 将参数复制到可变变量中,便于后续修改var result = 0 // 初始化反转结果为 0// 当 x 不为 0 时,继续处理while x != 0 {let pop = x % 10 // 取出最低位(如 123 % 10 = 3)x /= 10 // 去掉最低位(如 123 / 10 = 12)// ----------- 溢出判断开始 -----------// 如果 result > INT_MAX / 10,那么 *10 一定会溢出// 如果 result == INT_MAX / 10,还要判断 pop 是否超过最大个位数 7(2147483647 的最后一位)if result > Int(INT_MAX) / 10 || (result == Int(INT_MAX) / 10 && pop > 7) {return 0 // 正数溢出,返回 0}// 如果 result < INT_MIN / 10,那么 *10 一定会溢出// 如果 result == INT_MIN / 10,还要判断 pop 是否小于最小个位数 -8(-2147483648 的最后一位)if result < Int(INT_MIN) / 10 || (result == Int(INT_MIN) / 10 && pop < -8) {return 0 // 负数溢出,返回 0}// ----------- 溢出判断结束 -----------result = result * 10 + pop // 将当前位加入结果中(完成“反转”的核心操作)}return result // 返回最终的反转结果
}
✅ 补充说明
为什么只判断 pop > 7 和 pop < -8?
因为 32 位整数最大值是 2147483647,最小值是 -2147483648,个位分别是 7 和 -8,所以边界判断时只需要关注个位数。
🔍 调试小技巧
你可以在 while 循环内部加上:
print("pop = \(pop), result = \(result), x = \(x)")
用来调试每一步取数和构建过程,非常适合教学和面试时解释思路。
📌 总结
这道题不光考察了基本的数学操作,还测试了你对 整数范围和边界条件的敏感性,是许多面试官非常喜欢的一道算法题。通过合理的判断条件,我们可以在不使用任何 64 位数据类型的情况下,完成这个操作,符合题目所有要求。
🎁 如果你想瞅瞅允许使用 64 位整数解法👇
func reverse(_ x: Int) -> Int {var x = xvar result: Int64 = 0 // 使用 64 位整数防止中间过程溢出while x != 0 {let pop = x % 10x /= 10result = result * 10 + Int64(pop)}// 最后检查是否落在 32 位整数范围内if result < Int64(Int32.min) || result > Int64(Int32.max) {return 0}return Int(result) // 转换回 Int(假设 Int 是 32 位或 64 位都没关系)
}
使用场景选择
• 如果你明确知道平台支持 64 位整数(如大部分 iOS/macOS 平台的 Int 实际是 64 位),并且题目没有禁止,使用 Int64 是更安全也更清晰的做法。
• 但在算法题或面试中,如果题目要求 “不能使用 64 位整数”,那就必须用前面那种严格的按位判断方式。
相关文章:

每日算法 -【Swift 算法】反转整数的陷阱与解法:Swift 中的 32 位整数处理技巧
反转整数的陷阱与解法:Swift 中的 32 位整数处理技巧 在面试题和算法练习中,整数反转是一道非常经典的题目。乍一看很简单,但一旦加入“不能使用 64 位整数”和“不能溢出 32 位整数范围”这两个限制,问题就立刻变得有挑战性。本…...

使用 OpenCV 实现“随机镜面墙”——多镜片密铺的哈哈镜效果
1. 引言 “哈哈镜”是一种典型的图像变形效果,通过局部镜面反射产生扭曲的视觉趣味。在计算机视觉和图像处理领域,这类效果不仅有趣,还能用于艺术创作、交互装置、视觉特效等场景。 传统的“哈哈镜”往往是针对整张图像做某种镜像或扭曲变换…...

鸿蒙仓颉开发语言实战教程:页面跳转和传参
前两天分别实现了商城应用的首页和商品详情页面,今天要分享新的内容,就是这两个页面之间的相互跳转和传递参数。 首先我们需要两个页面。如果你的项目中还没有第二个页面,可以右键cangjie文件夹新建仓颉文件: 新建的文件里面没什…...

如何在Vue中实现延迟刷新列表:以Element UI的el-switch为例
如何在Vue中实现延迟刷新列表:以Element UI的el-switch为例 在开发过程中,我们经常需要根据用户操作或接口响应结果来更新页面数据。本文将以Element UI中的el-switch组件为例,介绍如何在状态切换后延迟1秒钟再调用刷新列表的方法࿰…...

最新Spring Security实战教程(十六)微服务间安全通信 - JWT令牌传递与校验机制
🌷 古之立大事者,不惟有超世之才,亦必有坚忍不拔之志 🎐 个人CSND主页——Micro麦可乐的博客 🐥《Docker实操教程》专栏以最新的Centos版本为基础进行Docker实操教程,入门到实战 🌺《RabbitMQ》…...

MDM在智能健身设备管理中的技术应用分析
近年来,随着智能硬件的普及和健身行业的数字化转型,越来越多健身房引入了Android系统的智能健身设备,如智能动感单车、智能跑步机、体测仪等。这些设备通过内嵌的安卓终端,实现了健身内容播放、用户交互、远程课程等功能ÿ…...

OSPF ABR汇总路由
一、OSPF ABR汇总配置(手工汇总) 📌 场景示例 假设ABR连接区域0和区域1,区域1内存在多个子网(如10.1.0.0/24、10.1.1.0/24),需将其手动汇总为10.0.0.0/8并通告至区域0。 🔧 配置命…...
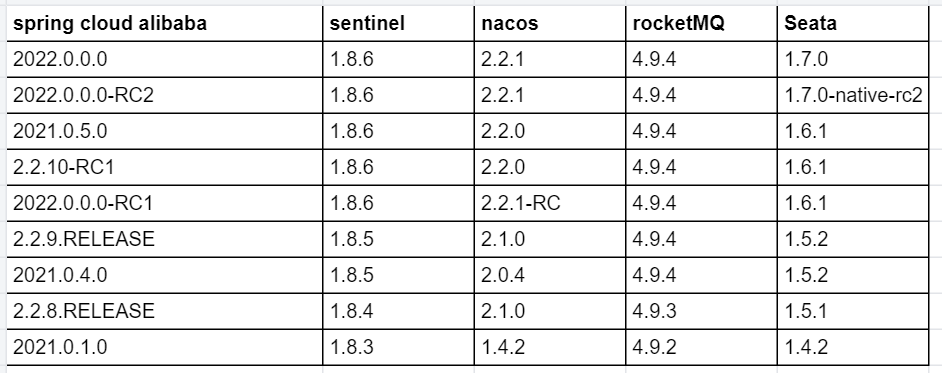
【五】Spring Cloud微服务开发:解决版本冲突全攻略
Spring Cloud微服务开发:解决版本冲突全攻略 目录 Spring Cloud微服务开发:解决版本冲突全攻略 概述 一、Spring Boot 二、Spring Cloud 三、Spring Cloud Alibaba 总结 概述 spring cloud微服务项目开发过程中经常遇到程序包版本冲突的问题&…...
Spring Boot微服务架构(二):开发调试常见中文问题
Spring Boot开发调试常见中文问题及解决方案 一、环境配置类问题 端口冲突 表现:启动时报错"Address already in use"解决:修改application.properties中的server.port或终止占用端口的进程 数据库连接失败 表现:启动时报错"…...
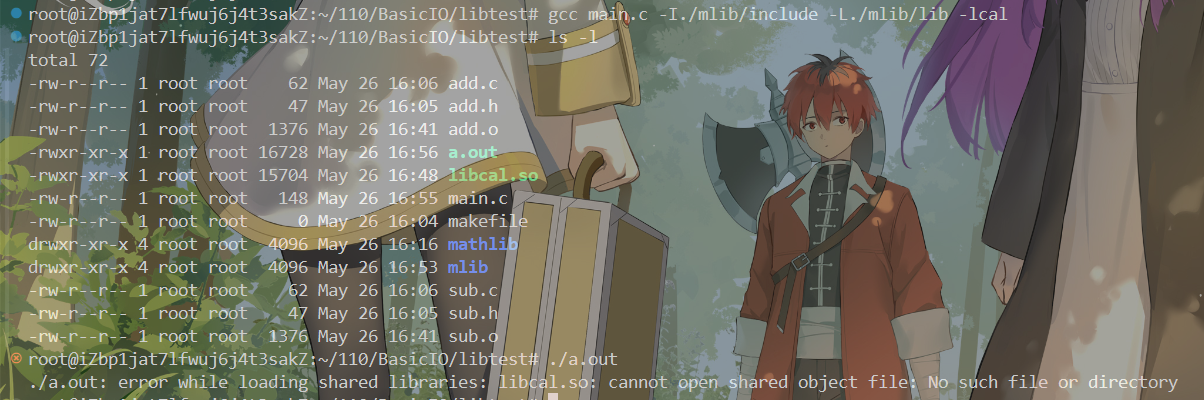
Linux基础IO----动态库与静态库
什么是库? 库是由一些.o文件打包在一起而形成的可执行程序的半成品。 如何理解这句话呢? 首先,一个程序在运行前需要进行预处理、编译、汇编、链接这几步。 预处理: 完成头文件展开、去注释、宏替换、条件编译等,最终…...
LeetCode百题刷004(哈希表优化两数和问题)
遇到的问题都有解决的方案,希望我的博客可以为你提供一些帮助 一、哈希策略优化两数和问题 题目地址:1. 两数之和 - 力扣(LeetCode)https://leetcode.cn/problems/two-sum/description/ 思路分析: 题目要求在一个整型…...
编码与new String()解码的字符集转换机制)
解析Java String.getBytes()编码与new String()解码的字符集转换机制
引言 在Java开发中,字符编码与解码是处理文本数据的基础操作,但稍有不慎就会导致乱码问题。理解字符串在内存中的存储方式以及如何正确使用编码转换方法,是保证跨平台、多语言兼容性的关键。本文将通过编码与解码的核心方法、常见问题场景及…...

从万有引力到深度学习,认识模型思维
从万有引力到深度学习,认识模型思维 引言 从牛顿发现万有引力定律到现代深度学习的崛起,“模型思维”始终是人类理解世界、解决问题的核心工具。它不仅是科学研究的基石,更是技术创新的底层逻辑。本文将从科学史、技术应用、认知效率等角度…...

2022 年 9 月青少年软编等考 C 语言八级真题解析
目录 T1. 道路思路分析T2. 控制公司思路分析T3. 发现它,抓住它思路分析T4. 青蛙的约会思路分析T1. 道路 题目链接:SOJ D1216 N N N 个以 1 ∼ N 1 \sim N 1∼N 标号的城市通过单向的道路相连,每条道路包含两个参数:道路的长度和需要为该路付的通行费(以金币的数目来表示…...

FPGA通信之VGA与HDMI
文章目录 VGA基本概念:水平扫描:垂直扫描: 时序如下:端口设计疑问为什么需要输出那么多端口不输出时钟怎么保证电子枪移动速度符合时序VGA转HDMI 仿真电路图代码总结:VGA看野火电子教程 HDMITMDS传输原理为什么使用TMD…...

Leetcode百题斩-二叉树
二叉树作为经典面试系列,那么当然要来看看。总计14道题,包含大量的简单题,说明这确实是个比较基础的专题。快速过快速过。 先构造一个二叉树数据结构。 public class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode…...

修改 K8S Service 资源类型 NodePort 的端口范围
在 Kubernetes 中,Service 类型为 NodePort 时,默认分配的端口范围为 30000~32767。如果你希望使用自定义端口(如 8080、8888 等),就需要修改 kube-apiserver 的默认配置。 本文将详细介绍如何修改 Kubernetes 中 Nod…...

ACM Latex模板:合并添加作者和单位
目录: 1.ACM会议论文Latex模板,逐个添加作者和单位: 1)Latex: 2)效果: 2. ACM会议论文Latex模板,合并添加作者和单位: 1)Latex: 2&#x…...

爬虫IP代理技术深度解析:场景、选型与实战应用
目录 一、代理IP的核心技术架构 二、典型应用场景技术解析 场景1:电商价格监控系统 场景2:社交媒体舆情分析 场景3:金融数据采集 三、代理IP选型方法论 1. 性能评估矩阵 2. 成本优化模型 3. 风险管控体系 四、未来技术演进方向 五、…...

将MCP(ModelContextProtocol)与Semantic Kernel集成(调用github)
文章目录 将MCP(ModelContextProtocol)与Semantic Kernel集成(调用github)一、模型上下文协议(MCP)简介1.1 简介1.2 示例 二、集成步骤2.1 安装环境依赖2.2 构建语义内核(Kernel)2.3…...

游戏引擎学习第311天:支持手动排序
仓库: https://gitee.com/mrxiao_com/2d_game_7(已满) 新仓库: https://gitee.com/mrxiao_com/2d_game_8 回顾并为今天的内容定下基调 我们接下来要继续完成之前开始的工作,上周五开始的部分内容,虽然当时对最终效果还不太确定,但现在主要任…...

LambdaQueryWrapper、MybatisPlus提供的基本接口方法、增删改查常用的接口方法、自定义 SQL
DAY26.2 Java核心基础 MybatisPlus提供的基本接口方法 分页查询 导入依赖springboot整合Mybatis-plus <dependency><groupId>com.baomidou</groupId><artifactId>mybatis-plus-boot-starter</artifactId><version>3.4.3</version&g…...

深度学习---可视化
模型可视化 深度学习模型可视化是理解、调试和优化模型的关键技术,涉及模型结构、参数、层输出、数据流动、训练过程等多维度分析。 一、可视化的核心作用 模型理解 解析复杂模型的网络架构(如CNN的层级连接、Transformer的注意力机制)。揭…...

军事大模型及其应用分析
一、军事大模型概述 在军事智能化浪潮下,大模型技术加速从理论迈向实战,成为重塑军事决策体系的核心力量,推动军事体系数字工程进入新阶段。 美国依托成熟的商业科技生态,率先推进大模型军事应用。Palantir 公司的 AIP 军事智能…...

c++算法题
题目 字符串的替换操作 replace(String &s, String &t, String &v) 是指: 若t是s的子串,则用串v替换串t在串s中的所有出现;若t不是s的子串,则串s不变。例如,若串s为“aabbabcbaabaaacbab”,串…...

云原生安全 SaaS :从基础到实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 1. 基础概念 什么是 SaaS? SaaS(Software as a Service,软件即服务)是一种基于云计算的软件交付模式。用…...

《Drain日志解析算法》论文阅读笔记
这篇文档介绍了一种名为Drain的在线日志解析方法,它采用固定深度的解析树进行流式日志处理 [cite: 1, 6]。 摘要 日志记录了宝贵的系统运行时信息,广泛应用于Web服务管理中 [cite: 1]。典型的日志分析过程首先需要解析原始日志消息,因为它们…...

MMAction2重要的几个配置参数
embed_dims(全称 embedding dimensions)是指每个 patch(块)或特征的通道数/维度,是 Transformer 或 Swin Transformer 等模型中最核心的特征表示维度。 embed_dims 必须能被 num_heads 整除 具体解释 在 Swin Transfo…...

Windows系统如何查看ssh公钥
很多人只是一味的为拿到ssh公钥而努力,往往却会忽略了ssh公钥与私钥背后的作用。 咱们在这里会花两分钟。 一分钟速通概念,一分钟教会你如何获取。 一分钟速通概念: 如何生成: SHH 公钥 与 私钥 是基于非对称加密算法ÿ…...

UniApp+Vue3微信小程序二维码生成、转图片、截图保存整页
二维码生成工具使用uqrcode/js,版本4.0.7 官网地址:uQRCode 中文文档(不建议看可能会被误导) 本项目采用了npm引入方式,也可通过插件市场引入,使用上会略有不同 准备工作: 安装:pnpm…...
