洛谷 P3374 【模板】树状数组 1(线段树解法)
【题目链接】
洛谷 P3374 【模板】树状数组 1
【题目考点】
1. 线段树
线段树(Segment tree)是一种用来维护区间信息的数据结构。
线段树中每个结点代表一个区间
根结点代表整体区间。
叶子结点代表长为1的单位区间。
对于线段树中的每一个分支结点 [ l , r ] [l, r] [l,r],m=(l+r)/2
- 左孩子表示的区间为 [ l , m ] [l, m] [l,m]
- 右孩子表示的区间为 [ m + 1 , r ] [m+1,r] [m+1,r]
线段树的设计思想为:分治思想
线段树的性质有:
- 线段树是平衡二叉树
- 线段树除去最后一层,是满二叉树。
- 区间长度为n的线段树的叶子结点数量为n。
- 区间长度为n的线段树的总结点数量为 2 n − 1 2n-1 2n−1。
- 任意两个结点或是包含关系,或者没有重叠部分。
- 区间长度为n的线段树的高度为 ⌈ log 2 n ⌉ + 1 \lceil \log_2n \rceil+1 ⌈log2n⌉+1。
- 用顺序存储结构存储区间长为n的线段树,需要数组长度不超过4n-1。因此常把数组长度设为4n。
- 任意长为L的子区间都可以被分成不超过 2 log 2 L 2\log_2L 2log2L个由线段树中结点表示的区间。
以上各性质的证明见:线段树相关性质证明
【解题思路】
首先线段树每个结点需要包含该结点表示的区间 [ l , r ] [l, r] [l,r],以及需要维护的该区间的加和。
使用树的顺序存储结构来保存线段树,表示线段树的数组是tree。
根据性质7,序列长度最大为 N N N时,数组长度需要开到 4 N 4N 4N。
struct Node
{int l, r;//当前结点表示区间[l, r]long long val;//区间[l, r]的加和为val
} tree[4*N];
在树的顺序存储结构中,结点地址即为tree数组的下标。地址为 i i i的结点的左孩子的地址为 2 i 2i 2i,右孩子的地址为 2 i + 1 2i+1 2i+1。
pushUp操作为使用孩子结点的值更新当前结点的值。本题中,孩子结点区间和的加和为当前结点表示的区间和。
void pushUp(int i)//更新地址为i的结点的值
{tree[i].val = tree[2*i].val+tree[2*i+1].val;
}
1. 建树
首先将数值序列输入到数组a。根据a序列建立线段树。
在建树过程中需要设置树中各个结点的区间、数值。
基本过程为:
先设置当前结点表示的区间。
如果当前结点为叶子结点,则设置该结点的值。
如果不是叶子结点,则先递归建立左子树,再递归建立右子树。
而后根据左右孩子的值确定当前结点的值。
建树的过程即为对线段树遍历的过程,根据性质4,线段树中总结点数量为 2 n − 1 2n-1 2n−1,因此建树操作的时间复杂度为 O ( n ) O(n) O(n)。
void build(int i, int l, int r)//构建根结点地址为i的表示区间[l, r]的线段树
{tree[i].l = l, tree[r].r = r;//设结点表示的区间if(l == r)//如果区间长度为1,该结点为叶子结点{tree[i].val = a[l];//原序列为a序列return;}int mid = (l+r)/2;build(2*i, l, mid);//递归构建左右子树build(2*i+1, mid+1, r);pushUp(i);//更新地址为i的结点的值
}
2. 单点修改
要使a序列中第x元素的值增加v,即完成a[x] += v,考虑线段树的变化。
首先在线段树中递归找到表示第x位置元素的叶子结点,将该结点的值修改,再不断向上回溯,回溯时使用孩子的值更新当前结点的值。
单点修改的函数递归调用次数与线段树高度成正比。根据性质6,线段树的高度为 O ( log n ) O(\log n) O(logn)量级,因此线段树的单点修改操作的时间复杂度为 O ( log n ) O(\log n) O(logn)。
void update(int i, int x, long long v)//在根结点地址为i的线段树中,进行单点修改a[x] += v
{if(x < tree[i].l || x > tree[i].r) return;if(tree[i].l == tree[i].r)//如果i是叶子结点 {tree[i].val += v;return;}update(2*i, x, v); update(2*i+1, x, v);pushUp(i);//更新地址为i的结点的值
}
3. 区间查询
要查询a序列给定区间 [ l , r ] [l, r] [l,r]中元素的加和,要做的是将 [ l , r ] [l, r] [l,r]区间划分为几个线段树中结点表示的区间,将这些区间的值加和。
要在某结点表示的区间中,返回 [ l , r ] [l, r] [l,r]中元素的加和:
首先判断当前结点表示的区间和 [ l , r ] [l, r] [l,r]是否有交集。如果没有交集则返回。
如果当前结点表示的区间完全被区间 [ l , r ] [l, r] [l,r]包含,则返回当前结点的值。
否则分别求出当前结点的两个子结点表示的区间中的且在 [ l , r ] [l, r] [l,r]中的元素的加和,将二者的加和返回。
每找到一个完全被 [ l , r ] [l, r] [l,r]包含的区间就返回。设 L = r − l + 1 L=r-l+1 L=r−l+1,而 L L L最大可以达到 n n n。根据性质8,可知这样的区间有 2 log 2 L 2\log_2L 2log2L个,是 O ( log n ) O(\log n) O(logn)量级。区间查询访问到的结点构成了线段树的一个子树,该子树的叶子结点表示的就是区间 [ l , r ] [l, r] [l,r]被线段树划分成的各个区间。
该树的叶子结点数是 O ( log n ) O(\log n) O(logn)的。
对于该树中度为1的结点,只有“左孩子表示的区间在 [ l , r ] [l, r] [l,r]外,右孩子表示的区间在 [ l , r ] [l, r] [l,r]内”,或“右孩子表示的区间在 [ l , r ] [l, r] [l,r]外,左孩子表示的区间在 [ l , r ] [l, r] [l,r]内”,只能最多在二叉树的左右两侧形成两条链,每条链的最大高度为 O ( log n ) O(\log n) O(logn)。
long long query(int i, int l, int r)
{//在根结点地址为i的线段树中,查询区间[l, r]中所有元素的和if(tree[i].r < l || tree[i].l > r)return 0; if(l <= tree[i].l && tree[i].r <= r)return tree[i].val;return query(2*i, l, r) + query(2*i+1, l, r);
}
【题解代码】
#include<bits/stdc++.h>
using namespace std;
#define N 500005
struct Node
{int val, l, r;
} tree[4*N];
int n, m, a[N];
void pushUp(int i)//更新tree[i]的值
{tree[i].val = tree[2*i].val+tree[2*i+1].val;
}
void build(int i, int l, int r)//建树 O(n)
{tree[i].l = l, tree[i].r = r;if(l == r){tree[i].val = a[l];return;}int mid = (l+r)/2;build(2*i, l, mid);build(2*i+1, mid+1, r);pushUp(i);
}
void update(int i, int x, int v)//单点修改:a[x] += v O(logn)
{if(x < tree[i].l || x > tree[i].r)return;if(tree[i].l == tree[i].r){tree[i].val += v;return;}update(2*i, x, v);update(2*i+1, x, v);pushUp(i);
}
int query(int i, int l, int r)//区间查询:a[l]+...+a[r] O(logn)
{if(tree[i].r < l || tree[i].l > r)return 0;if(l <= tree[i].l && tree[i].r <= r)return tree[i].val;return query(2*i, l, r)+query(2*i+1, l, r);
}
int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int op, x, k, y;cin >> n >> m;for(int i = 1; i <= n; ++i)cin >> a[i];build(1, 1, n);for(int i = 1; i <= m; ++i){cin >> op;if(op == 1){cin >> x >> k;update(1, x, k);} else{cin >> x >> y;cout << query(1, x, y) << '\n';}}return 0;
}相关文章:
)
洛谷 P3374 【模板】树状数组 1(线段树解法)
【题目链接】 洛谷 P3374 【模板】树状数组 1 【题目考点】 1. 线段树 线段树(Segment tree)是一种用来维护区间信息的数据结构。 线段树中每个结点代表一个区间 根结点代表整体区间。 叶子结点代表长为1的单位区间。 对于线段树中的每一个分支结点 [ l , r ] [l, r] [l,r]…...

欣佰特科技| SIL2/PLd 认证 Inxpect毫米波安全雷达:3D 扫描 + 微小运动检测守护工业安全
Inxpect 成立于意大利,专注工业安全技术。自成立起,便致力于借助先进雷达技术提升工业自动化安全标准,解决传统安全设备在复杂环境中的局限,推出获 SIL2/PLd 和 UL 认证的安全雷达产品。 Inxpect 的雷达传感器技术优势明显。相较于…...

大模型量化原理
模型量化的原理是通过降低数值精度来减少模型大小和计算复杂度。让我详细解释其核心原理:我已经为您创建了一个全面的模型量化原理详解文档。总结几个核心要点: 量化的本质 量化的核心是精度换性能的权衡——通过降低数值精度(FP32→INT8&a…...

dify-api的.env配置文件
源码位置:dify\api\.env 本文使用Dify v1.3.1。配置文件中各变量的详细信息表,如下所示: 变量英文名变量中文名默认值变量功能SECRET_KEY秘密密钥XXX用于安全地签署会话cookie的应用秘密密钥。确保在部署时使用强密钥。CONSOLE_API_URL控制…...
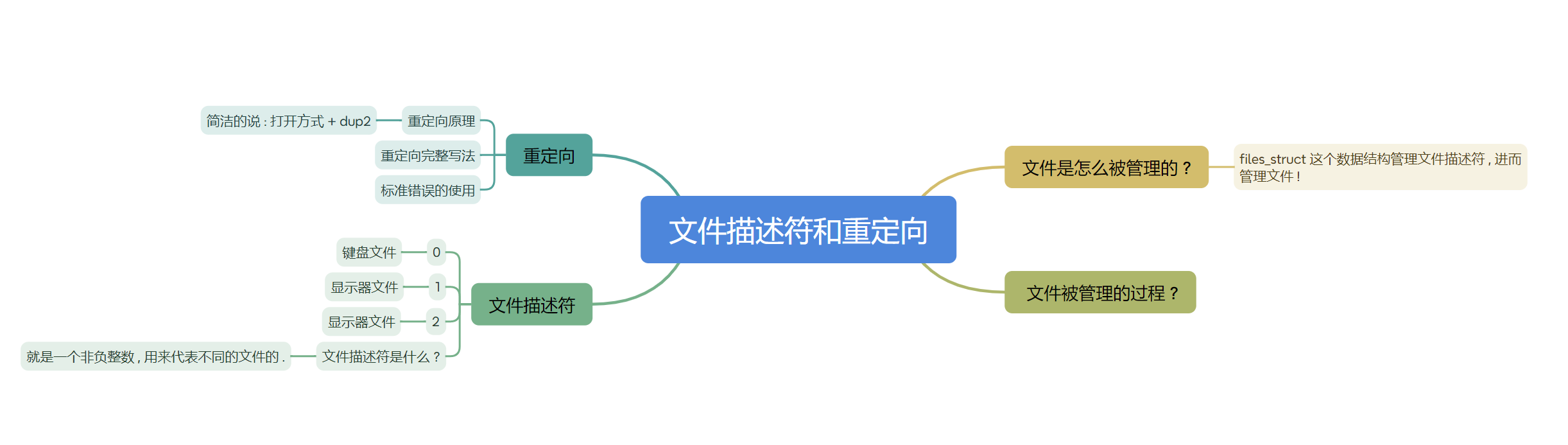
【Linux】Linux 操作系统 - 18 , 重谈文件(二) ~ 文件描述符和重定向原理 , 手把手带你彻底理解 !!!
文章目录 ● 文件描述符一 、Linux 系统对文件的管理(要知道)二 、什么是文件描述符 fd ?三 、再探文件被管理过程(重要)四 、文件描述符 0 、1、21. 文件描述符的分配原则2. 提前认识三个默认打开的文件 ● 重定向原理(重要)一 、重定向现象二 、深入剖析重定向现象(重要)1…...
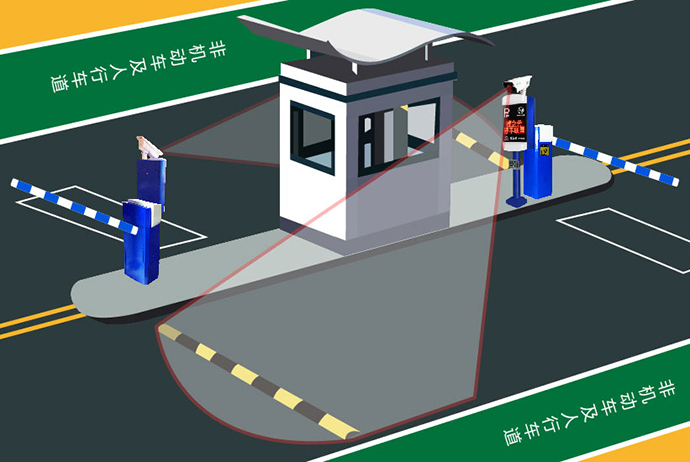
第五十三节:综合项目实践-车牌识别系统
一、项目背景与意义 车牌识别系统(LPR)是智能交通领域的核心技术之一,广泛应用于停车场管理、违章抓拍、高速公路收费等场景。本文将通过Python+OpenCV实现一个完整的车牌识别系统,涵盖图像预处理→车牌定位→字符分割→字符识别四大核心环节。 二、系统架构设计 技术栈组…...
)
AI时代新词-AI伦理(AI Ethics)
一、什么是AI伦理? AI伦理(AI Ethics)是指在人工智能(AI)的设计、开发、部署和使用过程中,涉及的道德、法律和社会问题的综合考量。它关注AI技术对人类社会、文化、价值观以及个人权利的影响,并…...

湖北理元理律师事务所债务优化服务中的“四维平衡“之道
债务问题解决需要兼顾多方利益,湖北理元理律师事务所通过独特的服务模式,在法律、经济、心理、社会四个维度建立平衡点。 一、法律维度的专业把控 合规性审查: 合同效力认定 诉讼时效核查 担保责任界定 程序合法性: 所有协…...

Git Push 失败:HTTP 413 Request Entity Too Large
Git Push 失败:HTTP 413 Request Entity Too Large 问题排查 在使用 Git 推送包含较大编译产物的项目时,你是否遇到过 HTTP 413 Request Entity Too Large 错误?这通常并不是 Git 的问题,而是 Web 服务器(如 Nginx&am…...

第10章 网络与信息安全基础知识
网络概述 多模光纤的特点:成本低,宽芯线,聚光好,耗散大,低效,用于低速度、短距离的通信。 单模光纤的特点:成本高,窄芯线,需要激光源,耗散小,高效…...
)
GO语言学习(九)
GO语言学习(九) 上一期我们了解了实现web的工作中极为重要的net/http抱的细节讲解,大家学会了实现web开发的一些底层基础知识,在这一期我来为大家讲解一下web工作的一个重要方法,:使用数据库,现…...

go 访问 sftp 服务 github.com/pkg/sftp 的使用踩坑,连接未关闭(含 sftp 服务测试环境搭建)
前言 最近在使用 sftp 服务时,被告知发起了海量的连接,直接把服务器搞崩,ip 被封了。 这是啥情况? golang 写的代码,我就正常的访问 sftp 服务,连接使用过后也都关闭了,咋会出现连接一直连着…...

Linux多线程(二)之进程vs线程
文章目录 Linux进程VS线程进程和线程进程的多个线程共享关于进程线程的问题 重谈地址空间Linux线程周边的概念 Linux进程VS线程 进程和线程 进程是资源分配的基本单位(进程是承担分配系统资源的基本实体) 执行流也是资源!线程是进程内部的执…...

【MogDB】测试 ubuntu server 22.04 LTS 安装mogdb 5.0.11
测试 ubuntu server 22.04 LTS 安装mogdb 5.0.11 使用的操作系统镜像是 https://releases.ubuntu.com/22.04/ubuntu-22.04.5-live-server-amd64.iso 装好操作系统后,把root登录打开了,方便后续操作。 测试过程 使用官方命令在线安装ptk rootubuntu22…...
)
AI时代新词-数字孪生(Digital Twin)
一、什么是数字孪生(Digital Twin)? 数字孪生(Digital Twin)是一种通过创建物理实体的虚拟副本,并利用数据和算法来模拟、分析和优化物理实体的性能和行为的技术。数字孪生结合了物联网(IoT&am…...

【HW系列】—web常规漏洞(文件上传漏洞)
文章目录 一、简介二、危害三、文件检测方式分类四、判断文件检测方式五、文件上传绕过技术六、漏洞防御措施 一、简介 文件上传漏洞是指Web应用程序在处理用户上传文件时,未对文件类型、内容、路径等进行严格校验和限制,导致攻击者可上传恶意文件&…...

如何实现 C/C++ 与 Python 的通信
C/C 与 Python 的通信可以通过多种方式实现,如使用 C API、Ctypes、Cython、SWIG、Python.h 或基于共享库的调用等。其中,使用 Ctypes 方式最为简便,适合快速调用已有的 C 函数库。例如,通过将 C 代码编译为动态链接库(…...

python炸鱼船
import pygame, random # 加载库 from pygame.locals import * pygame.init() pygame.display.set_caption("炸渔船") canvas pygame.display.set_mode((700, 500)) bgpygame.image.load("bg.png") bgpygame.transform.scale(bg,(700,500))class Hero(py…...

使用AutoKeras2.0的AutoModel进行结构化数据回归预测
1、First of All: Read The Fucking Source Code import autokeras as ak import numpy as np from sklearn.model_selection import train_test_split from sklearn.metrics import mean_squared_error# 生成数据集 np.random.seed(42) x np.random.rand(1000, 10) # 生成1…...

好用但不常用的Git配置
参考文章 文章目录 tag标签分支新仓库默认分支推送 代码合并冲突处理默认diff算法 tag标签 默认是以字母顺序排序,这会导致一些问题,比如0.5.101排在0.5.1000之后。为了解决这个问题,我们可以把默认排序改为数值排序 git config --global t…...

ULVAC VWR-400M/ERH 真空蒸发器 Compact Vacuum Evaporator DEPOX (VWR-400M/ERH)
ULVAC VWR-400M/ERH 真空蒸发器 Compact Vacuum Evaporator DEPOX (VWR-400M/ERH)...

P1068 [NOIP 2009 普及组] 分数线划定
题目描述 世博会志愿者的选拔工作正在 A 市如火如荼的进行。为了选拔最合适的人才,A 市对所有报名的选手进行了笔试,笔试分数达到面试分数线的选手方可进入面试。面试分数线根据计划录取人数的 150% 划定,即如果计划录取 m 名志愿者…...

PPT连同备注页(演讲者模式)一块转为PDF
首先,进入创建PDF/XPS: 然后进入选项: 发布选项-发布内容里选备注页: 导出的原始结果是这样的: 这个时候裁剪一下,范围为所有页面: 最终结果: 如果导出不选“备注页”而是只勾选“包…...

第三十二天打卡
作业:参考pdpbox官方文档中的其他类,绘制相应的图,任选即可 1. 安装并导入库 确保安装与文档版本一致的 pdpbox(此处以 0.3.0 为例): bash 复制 下载 pip install pdpbox0.3.0 导入所需库:…...

项目三 - 任务8:实现词频统计功能
本项目旨在实现一个词频统计功能,通过读取文本文件并利用Java编程技巧处理和分析文本数据。首先,使用BufferedReader逐行读取文件内容,然后通过String.split(" ")方法将每行文本分割成单词数组。接下来,采用HashMap来存…...

MongoDB 快速整合 SpringBoot 示例
1.添加依赖<dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-web</artifactId></dependency><dependency><groupId>org.springframework.boot</groupId><artifactId>spr…...

2025.05.22-得物春招机考真题解析-第二题
📌 点击直达笔试专栏 👉《大厂笔试突围》 💻 春秋招笔试突围在线OJ 👉 笔试突围OJ 02. 魔法书页重排 问题描述 A先生是一位魔法师,他有一本古老的魔法书,书中有 n n n 页,每页都刻有一个魔…...

ollama list模型列表获取 接口代码
ollama list模型列表获取 接口代码 curl http://localhost:11434/v1/modelscoding package hcx.ollama;/*** ClassName DockerOllamaList* Description TODO* Author dell* Date 2025/5/26 11:31* Version 1.0**/import java.io.BufferedReader; import java.io.InputStreamR…...

OPC Client第5讲(wxwidgets):初始界面的事件处理;按照配置文件初始化界面的内容
接上一讲,即实现下述界面的事件处理代码;并且按照配置文件初始化界面的内容(三、) 事件处理的基础知识,见下述链接五、 OPC Client第3讲(wxwidgets):wxFormBuilder;基础…...

什么是BFC,如何触发BFC,BFC有什么特性?
理解 BFC指的是块级格式化上下文,处于BFC内部的盒子与外界互不影响 触发条件 position:absolute/fixed都会产生bfcdisplay:inline-block,table,flex等float:left/right 浮动也会产生bfchtml根元素也是bfc bfc的特性 属于同一个BFC下的盒子会垂直排列属于同一个BFC下的两个…...
