[原创](计算机数学)(The Probability Lifesaver)(P14): 推导计算 In(1-u) 约等于 -u
[作者]
常用网名: 猪头三
出生日期: 1981.XX.XX
企鹅交流: 643439947
个人网站: 80x86汇编小站
编程生涯: 2001年~至今[共24年]
职业生涯: 22年
开发语言: C/C++、80x86ASM、Object Pascal、Objective-C、C#、R、Python、PHP、Perl、
开发工具: Visual Studio、Delphi、XCode、C++ Builder、Eclipse
技能种类: 逆向 驱动 磁盘 文件 大数据分析
涉及领域: Windows应用软件安全/Windows系统内核安全/Windows系统磁盘数据安全/macOS应用软件安全
项目经历: 股票模型量化/磁盘性能优化/文件系统数据恢复/文件信息采集/敏感文件监测跟踪/网络安全检测
专注研究: 机器学习、股票模型量化、金融分析
[描述]
用 Taylor 定理(带余项的形式)来严格推导
ln ( 1 − u ) = − u − u 2 2 − u 3 3 − ⋯ ≈ − u \ln(1 - u) \;=\;-u \;-\;\frac{u^2}{2}\;-\;\frac{u^3}{3}\;-\cdots \;\approx\;-u ln(1−u)=−u−2u2−3u3−⋯≈−u
重点在于写出"余项"(remainder)的表达式, 并说明它为什么相对第一项很小, 从而可以忽略. 以下分几步来展开.
1. Taylor 定理(拉格朗日余项形式)概述
设 f f f 在 a a a 的某邻域内具有 n + 1 n+1 n+1 阶连续导数, 那么在点 a a a 处对 f ( x ) f(x) f(x) 做 n n n 阶 Taylor 展开, 有:
f ( x ) = P n ( x ) + R n ( x ) f(x) \;=\; P_n(x) \;+\; R_n(x) f(x)=Pn(x)+Rn(x)
其中
-
P n ( x ) P_n(x) Pn(x) 是关于 a a a 点的 n n n 阶 Taylor 多项式:
P n ( x ) = f ( a ) + f ′ ( a ) ( x − a ) + f ′ ′ ( a ) 2 ! ( x − a ) 2 + ⋯ + f ( n ) ( a ) n ! ( x − a ) n P_n(x) \;=\; f(a) \;+\; f'(a)(x-a) \;+\; \frac{f''(a)}{2!}(x-a)^2 \;+\;\cdots+\; \frac{f^{(n)}(a)}{n!}(x-a)^n Pn(x)=f(a)+f′(a)(x−a)+2!f′′(a)(x−a)2+⋯+n!f(n)(a)(x−a)n
-
R n ( x ) R_n(x) Rn(x) 是 Lagrange 格式的余项:
R n ( x ) = f ( n + 1 ) ( ξ ) ( n + 1 ) ! ( x − a ) n + 1 , 对某个 ξ 在 a 与 x 之间. R_n(x) \;=\; \frac{f^{(n+1)}(\xi)}{(n+1)!}\,(x - a)^{\,n+1}, \quad \text{对某个 } \xi \text{ 在 }a\text{ 与 }x\text{ 之间.} Rn(x)=(n+1)!f(n+1)(ξ)(x−a)n+1,对某个 ξ 在 a 与 x 之间.
在本题中, 令
f ( u ) = ln ( 1 − u ) , a = 0 f(u) = \ln(1 - u), \qquad a = 0 f(u)=ln(1−u),a=0
希望展开到一阶(即 n = 1 n=1 n=1), 然后考察余项 R 1 ( u ) R_1(u) R1(u) 的大小.
2. 计算各阶导数, 并写出一阶多项式与余项
对 f ( u ) = ln ( 1 − u ) f(u)=\ln(1 - u) f(u)=ln(1−u), 在 u = 0 u=0 u=0 处计算导数:
-
f ( u ) = ln ( 1 − u ) f(u) = \ln(1 - u) f(u)=ln(1−u).
-
第一阶导数:
f ′ ( u ) = d d u [ ln ( 1 − u ) ] = − 1 1 − u f'(u) = \frac{d}{du}\bigl[\ln(1-u)\bigr] = -\,\frac{1}{1 - u} f′(u)=dud
相关文章:
(The Probability Lifesaver)(P14): 推导计算 In(1-u) 约等于 -u)
[原创](计算机数学)(The Probability Lifesaver)(P14): 推导计算 In(1-u) 约等于 -u
[作者] 常用网名: 猪头三 出生日期: 1981.XX.XX 企鹅交流: 643439947 个人网站: 80x86汇编小站 编程生涯: 2001年~至今[共24年] 职业生涯: 22年 开发语言: C/C++、80x86ASM、Object Pascal、Objective-C、C#、R、Python、PHP、Perl、 开发工具: Visual Studio、Delphi、XCode、…...

wordcount在集群上的测试
1.将louts.txt文件从cg计算机复制到master节点上面,存放在/usr/local/hadoop 需要输入密码:83953588abc scp /root/IdeaProjects/mapReduceTest/lotus.txt root172.18.0.2:/usr/local/hadoop /WordCountTest/input 2.将lotus.txt文件从master这台机器…...

OpenCV CUDA模块图像过滤------创建一个 Sobel 滤波器函数createSobelFilter()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 该函数用于创建一个 Sobel 滤波器,用于在 GPU 上进行边缘检测。它基于图像的梯度计算: dx 表示对 x 方向求导的阶数&…...

[面试精选] 0053. 最大子数组和
文章目录 1. 题目链接2. 题目描述3. 题目示例4. 解题思路5. 题解代码6. 复杂度分析 1. 题目链接 53. 最大子数组和 - 力扣(LeetCode) 2. 题目描述 给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一…...

怎么判断一个Android APP使用了Cordova这个跨端框架
要判断一个 Android 应用是否使用了 Cordova 框架,可以通过以下方法逐步验证: 一、安装包结构分析 1. 解压 APK 将 .apk 文件重命名为 .zip 并解压,检查以下特征文件: • assets/www/ 目录: Cordova 的核心 Web 资源&…...

PDF 转 JPG 图片小工具:CodeBuddy 助力解决转换痛点
本文所使用的 CodeBuddy 免费下载链接:腾讯云代码助手 CodeBuddy - AI 时代的智能编程伙伴 前言 在数字化办公与内容创作的浪潮中,将 PDF 文件转换为 JPG 图片格式的需求日益频繁。无论是学术文献中的图表提取,还是宣传资料的视觉化呈现&am…...

VisionPro 与 C# 联合编程:相机连接实战指南
在工业视觉检测与自动化领域,康耐视(Cognex)的 VisionPro 是一款功能强大的视觉开发工具,而 C# 凭借其简洁性与高效性,成为许多开发者的首选编程语言。本文将详细介绍如何通过 C# 与 VisionPro 联合编程实现相机连接&a…...

鸿蒙OSUniApp 实现动态的 tab 切换效果#三方框架 #Uniapp
使用 UniApp 实现动态的 tab 切换效果 在移动应用开发中,tab 切换(标签页)是提升界面组织性和用户体验的常用交互方式。无论是资讯、商城、社区还是管理后台,tab 组件都能帮助用户高效切换不同内容区域。随着 HarmonyOSÿ…...
:深度剖析Dockerfile与图形化容器实战 --- 3种容器构建方法对比与性能调优)
Docker系列(三):深度剖析Dockerfile与图形化容器实战 --- 3种容器构建方法对比与性能调优
引言 在云原生技术驱动软件交付革新的当下,Dockerfile 作为容器化技术的核心载体,通过声明式语法将应用环境固化为可复现、可版本化的“蓝图”,彻底终结了“开发-生产”环境割裂的顽疾。本文以 Ubuntu 24.04 LTS 为实践基础,深度…...
论文阅读:Next-Generation Database Interfaces:A Survey of LLM-based Text-to-SQL
地址:Next-Generation Database Interfaces: A Survey of LLM-based Text-to-SQL 摘要 由于用户问题理解、数据库模式解析和 SQL 生成的复杂性,从用户自然语言问题生成准确 SQL(Text-to-SQL)仍是一项长期挑战。传统的 Text-to-SQ…...

OS面试篇
用户态和内核态 用户态和内核态的区别? 内核态和用户态是操作系统中的两种运行模式。它们的主要区别在于权限和可执行的操作: 内核态(Kernel Mode):在内核态下,CPU可以执行所有的指令和访问所有的硬件资…...

FFMPEG-FLV-MUX编码
一、流程图 二、结构体 1 .AVOutputFormat 一、核心功能与作用 封装格式描述 AVOutputFormat保存了输出容器格式的元数据,包括: 短名称(name):如flv、mp4;易读名称(long_name)&…...

青少年编程与数学 02-020 C#程序设计基础 05课题、数据类型
青少年编程与数学 02-020 C#程序设计基础 05课题、数据类型 一、数据类型及其意义1. 数据类型的概念1.1 值类型(Value Types)1.2 引用类型(Reference Types) 2. 数据类型的重要性2.1 类型安全示例 2.2 内存管理示例 2.3 性能优化示…...

React vs Vue.js:选哪个框架更适合你的项目?
摘要 前端开发江湖里,React 和 Vue.js 堪称两大 “顶流” 框架,不少开发者在选择时都犯了难。用 React 吧,听说它性能超强,可学习曲线也陡峭;选 Vue.js,有人夸它上手快,但又担心功能不够强大。…...

Kafka|基础入门
文章目录 快速了解Kafka快速上手Kafka理解Kafka的集群Kafka集群的消息流转模型 快速了解Kafka 快速上手Kafka 启动zookeeper 启动kafka 创建topic - 启动发送者 - 启动消费者 Partition 0: [msg1] -> [msg2] -> [msg3] -> ...0 1 2Partition 1: [msg4…...

ADS学习笔记(五) 谐波平衡仿真
参考书籍:见资源绑定,书籍4.2 谐波平衡仿真 本文为对实验内容的补充 1. 三阶交调点坐标系图分析 我们来分析图1.5中“三阶交调点”坐标系图里的两条直线分别代表什么。 图中有两条向上倾斜的直线: 斜率较低的那条直线代表:基波输出功率 (Fundamental Out…...

MySQL存储引擎对比及选择指南
MySQL 存储引擎是数据库底层管理数据存储和操作的核心组件,不同存储引擎在事务支持、性能、锁机制、存储方式等方面存在显著差异。以下是常见存储引擎的对比及其适用场景: 1. InnoDB 事务支持:支持 ACID 事务(COMMIT/ROLLBACK&am…...

【IDEA问题】springboot本地启动应用报错:程序包不存在;找不到符号
问题: springboot本地启动应用报错: 程序包xxx不存在;找不到符号 解决方案: 1.确保用maven重新导入依赖 2.删除.idea文件夹 3.invalidate caches里,把能选择的都勾选上,然后清除缓存重启 4.再在上方工具栏…...

PETR- Position Embedding Transformation for Multi-View 3D Object Detection
旷视 ECCV 2022 纯视觉BEV方案transformer网络3D检测 paper:[2203.05625] PETR: Position Embedding Transformation for Multi-View 3D Object Detection code:GitHub - megvii-research/PETR: [ECCV2022] PETR: Position Embedding Transformation …...

Prompt Tuning与自然语言微调对比解析
Prompt Tuning 与输入提示词自然语言微调的区别和联系 一、核心定义与区别 维度Prompt Tuning(提示微调)输入提示词自然语言微调本质优化连续向量空间中的提示嵌入(不可直接阅读)优化离散自然语言文本(人类可理解)操作对象模型输入嵌入层的连续向量(如WordEmbedding)自…...

二十七、面向对象底层逻辑-SpringMVC九大组件之HandlerAdapter接口设计
在 Spring MVC 框架中,HandlerAdapter 是一个看似低调却极为关键的组件。它的存在,不仅解决了不同类型处理器(Handler)的调用难题,更体现了框架设计中对解耦、扩展性和模块化的深刻思考。本文将从接口设计的角度&#…...
QT软件开发环境及简单图形的绘制-图形学(实验一)-[成信]
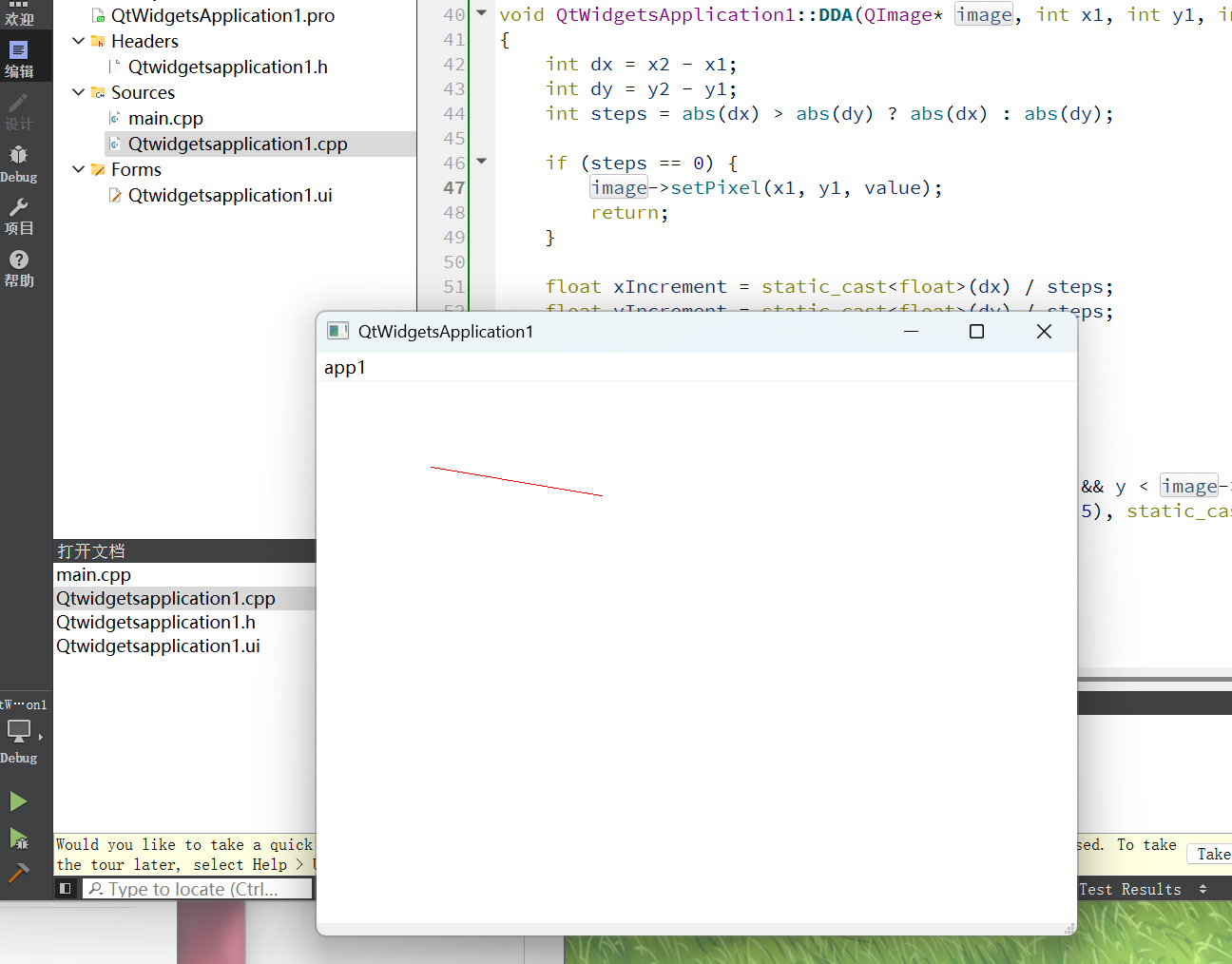
对于软件的安装这里就不多介绍了。 本文章主要是根据本校图形学的实验知道来做。 创建一个简单的计算机图形学程序 第一步:创建项目及配置 这里创建的项目名和类名尽量和我的一样,避免后面直接复制我的代码时会出现一些名字上面的错误。QtWidgetsAppl…...

项目部署一次记录
链路:(用户)客户端 → Nginx:192.168.138.100→ Tomcat (程序):192.168.138.101→ MySQL/Redis 打开数据库:systemctl start mysqld 重启网络: systemctl restart NetworkManager 关闭防火墙&am…...

单例模式,饿汉式,懒汉式,在java和spring中的体现
目录 饿汉式单例模式 懒汉式单例模式 Spring中的单例模式 关键差异对比 在Java和Spring中的应用场景 手写案例 单例模式是一种创建型设计模式,其核心在于确保一个类仅有一个实例,并提供一个全局访问点来获取该实例。下面将详细介绍饿汉式和懒汉式…...

一文带你彻底理清C 语言核心知识 与 面试高频考点:从栈溢出到指针 全面解析 附带笔者手写2.4k行代码加注释
引言:C 语言的魅力与挑战 从操作系统内核到嵌入式系统,从高性能计算到网络编程,C 语言高效、灵活和贴近硬件的特性,始终占据着不可替代的地位。然而,C 语言的强大也伴随着较高的学习曲线,尤其是指针、内存管…...

【Redis】第1节|Redis服务搭建
一、Redis 基础概念 核心功能 内存数据库,支持持久化(RDB/AOF)、主从复制、哨兵高可用、集群分片。常用场景:缓存、分布式锁、消息队列、计数器、排行榜等。 安装环境 依赖 GCC 环境(C语言编译)࿰…...

数据结构第5章 树与二叉树(竟成)
第 5 章 树与二叉树 【考纲内容】 1.树的基本概念 2.二叉树 (1)二叉树的定义及其主要特征 (2)二叉树的顺序存储结构和链式存储结构 (3)二叉树的遍历 (4)线索二叉树的基本概念和构造 …...

# 深入解析BERT自然语言处理框架:原理、结构与应用
深入解析BERT自然语言处理框架:原理、结构与应用 在自然语言处理(NLP)领域,BERT(Bidirectional Encoder Representations from Transformers)框架的出现无疑是一个重要的里程碑。它凭借其强大的语言表示能…...

ai学习--python部分-1.变量名及命名空间的存储
初学代码时总有一个问题困扰我:a 10 # a指向地址0x1234(存储10) 变量a的值10存储在0x1234,那么变量a需要存储吗?a又存储在什么地址呢 目录 1. 命名空间的本质 2. 命名空间的内存占用 3. …...

Cadence学习笔记之---PCB过孔替换、封装更新,DRC检查和状态查看
目录 01 | 引 言 02 | 环境描述 03 | 过孔替换 04 | 封装更新 05 | PCB状态查看 06 | DRC检查 07 | 总 结 01 | 引 言 终于终于来到了Cadence学习笔记的尾声! 在上一篇文章中,讲述了如何布线、如何铺铜,以及布线、铺铜过程中比较重要…...
