经典密码学和现代密码学的结构及其主要区别(2)维吉尼亚密码—附py代码
Vigenère cipher 维吉尼亚密码
维吉尼亚密码由布莱斯·德·维吉尼亚在 16 世纪发明,是凯撒密码的一个更复杂的扩展。它是一种多字母替换密码,使用一个关键字来确定明文中不同字母的多个移位值。
与凯撒密码不同,凯撒密码对所有字母都有固定的偏移量,而维吉尼亚密码使用一个重复的关键词为消息中的每个字母创建不同的偏移量。这使其更能抵御频率分析,但如果消息的一部分已知,它仍然容易受到已知明文攻击。维吉尼亚密码曾被认为相当安全,但用现代密码分析技术可以破解。
凯撒密码和维吉尼亚密码都是早期加密方法的历史实例。虽然它们易于理解,并在密码学史上发挥了重要作用,但它们缺乏现代加密应用所需的强大安全性,不适合保护敏感的数字信息。
维吉尼亚密码的主要特点
- 密钥。维吉尼亚密码使用一个关键字或短语作为加密和解密消息的密钥。关键字可以是任意长度,并通常重复以匹配明文的长度。
- 多字母表密码。与凯撒密码不同,凯撒密码对所有字符使用固定的移位值,维吉尼亚密码采用多字母表的方法。这意味着消息的不同部分可能会有不同的移位量,使其更复杂且更安全。
- 字母表。为了执行加密和解密,使用维吉尼亚表(也称为维吉尼亚方阵或正方形表)。该表由多个字母表的行和列组成,每行代表不同的凯撒密码移位。
• 加密过程
- 要加密一条消息,您需要将明文和关键词对齐。
- 对于明文中的每个字母,您都要在维吉尼亚密码表中找到由密钥中相应字母所确定的行。
- 然后找到与你想要加密的明文字母相对应的那一列。
- 行与列的交叉点即为密文字母。
- 对明文中的每个字母重复此过程。
• 解密过程
- 用维吉尼亚密码进行解密的过程与加密正好相反。
- 将密文与关键词对齐,就像加密时那样。
- 对于密文中的每个字母,根据关键字中的相应字母在维吉尼亚密码表中找到对应的行。
- 找到包含密文字母的那一列。
- 行与列的交叉点给出的就是明文字母。
- 对密文中的每个字母都重复此过程。
维吉尼亚密码比简单的凯撒密码更安全,因为它通过密钥引入了变化性。这使得频率分析和暴力破解攻击更具挑战性。但维吉尼亚密码的安全性仍然有限,尤其是在使用较短密钥时。较长的密钥能提高安全性。它容易受到卡西斯基检验的攻击,一种能够帮助识别密文中重复模式的技术,并有可能揭示有关密钥长度的信息。
🔹🔹🔹
假设有 m = 7 ,且关键字为 PHYSICS。对应于数值等价 K = (8, 0, 17, 11, 1, 21, 11)。
C i = ( M i + K i m o d m ) m o d 26 C_i = (M_i + K_{i \mod m}) \mod 26 Ci=(Mi+Kimodm)mod26 其中 M i M_i Mi为明文字母数值(A=0), K j K_j Kj为密钥字母数值, m m m为密钥长度。
- m m m:密钥长度(此处 m = 7 )
- M i M_i Mi:明文中第 i 个字符的数值( a=0, b=1,…, z=25 )
- K j K_j Kj:密钥中第j个字符的数值( j = i mod m )
- C i C_i Ci:密文中第i个字符的数值

密文结果为:uaitvntclzlohtpazwfnncpyjtdnabfzl
解密时将使用相同的关键字,但要从密文中减去它,而不是加上它。
例如:
明文 m(索引: i = 0 ):
C i C_i Ci = (12 + 8) mod 26 = 20
密文是: u
py代码示例(仅供参考):
plaintext = "mariusiulianmihailescuphysicsbook"
key = [8, 0, 17, 11, 1, 21, 11]
ciphertext = []for i, char in enumerate(plaintext):# 将明文字符转换为0-25的数值p = ord(char) - ord('a')# 获取对应的密钥k = key[i % 7]# 加密并转换回字符encrypted_char = chr((p + k) % 26 + ord('a'))ciphertext.append(encrypted_char)# 将密文字符列表转换为字符串
ciphertext_str = ''.join(ciphertext)
print(ciphertext_str)
运行结果:

相关文章:

经典密码学和现代密码学的结构及其主要区别(2)维吉尼亚密码—附py代码
Vigenre cipher 维吉尼亚密码 维吉尼亚密码由布莱斯德维吉尼亚在 16 世纪发明,是凯撒密码的一个更复杂的扩展。它是一种多字母替换密码,使用一个关键字来确定明文中不同字母的多个移位值。 与凯撒密码不同,凯撒密码对所有字母都有固定的偏移…...

Elasticsearch 节点角色详解及协调节点请求策略
引言 Elasticsearch 集群中的节点可以承担多种角色,如主节点、数据节点、预处理节点和协调节点。合理配置和理解这些节点角色,对于保障集群的高可用性、性能优化以及请求调度至关重要。本文将深入解析各类节点的职责与配置方式,并介绍如何通…...

视频逐帧提取图片的工具
软件功能:可以将视频逐帧提取图片,可以设置每秒提取多少帧,选择提取图片质量测试环境:Windows 10软件设置:由于软件需要通过FFmpeg提取图片,运行软件前请先设置FFmpeg,具体步骤 1. 请将…...

数据结构第1章编程基础 (竟成)
第 1 章 编程基础 1.1 前言 因为数据结构的代码大多采用 C 语言进行描述。而且,408 考试每年都有一道分值为 13 - 15 的编程题,要求使用 C/C 语言编写代码。所以,本书专门用一章来介绍 408 考试所需的 C/C 基础知识。有基础的考生可以快速浏览…...

互联网大厂Java求职面试:AI大模型与云原生架构融合中的挑战
互联网大厂Java求职面试:AI大模型与云原生架构融合中的挑战 在互联网大厂的Java求职面试中,面试官往往以技术总监的身份,针对候选人对AI、大模型应用集成、云原生和低代码等新兴技术的理解与实践能力进行考察。以下是一个典型的面试场景&…...

msql的乐观锁和幂等性问题解决方案
目录 1、介绍 2、乐观锁 2.1、核心思想 2.2、实现方式 1. 使用 version 字段(推荐) 2. 使用 timestamp 字段 2.3、如何处理冲突 2.4、乐观锁局限性 3、幂等性 3.1、什么是幂等性 3.2、乐观锁与幂等性的关系 1. 乐观锁如何辅助幂等性…...

Python 实现桶排序详解
1. 核心原理 桶排序是一种非比较型排序算法,通过将数据分配到多个“桶”中,每个桶单独排序后再合并。其核心步骤包括: 分桶:根据元素的范围或分布,将数据分配到有限数量的桶中。桶内排序:对每个非空桶内的…...
——编码器(Encoder)、解码器(Decoder))
大模型(5)——编码器(Encoder)、解码器(Decoder)
文章目录 一、编码器(Encoder)1. 核心作用2. 典型结构(以Transformer为例)3. 应用场景 二、解码器(Decoder)1. 核心作用2. 典型结构(以Transformer为例)3. 应用场景 三、编码器与解码…...

Web3怎么本地测试连接以太坊?
ETHEREUM_RPC_URLhttps://sepolia.infura.io/v3/你的_INFURA_API_KEY 如果你没有 Infura Key,注册 Infura 或 Alchemy,拿一个免费测试网节点就行: Infura:https://infura.io Alchemy:Alchemy - the web3 developme…...
)
Vue-02 (使用不同的 Vue CLI 插件)
使用不同的 Vue CLI 插件 Vue CLI 插件扩展了 Vue 项目的功能,让你可以轻松集成 TypeScript、Vuex、路由等功能。它们可以自动进行配置和设置,从而节省您的时间和精力。了解如何使用这些插件对于高效的 Vue 开发至关重要。 了解 Vue CLI 插件 Vue CLI…...

理解vue-cli 中进行构建优化
在 Vue CLI 项目中进行构建优化,是前端性能提升的重要手段。它涉及到 Webpack 配置、代码分包、懒加载、依赖优化、图片压缩等多个方面。 🧱 基础构建优化 设置生产环境变量 NODE_ENVproduction Vue CLI 会自动在 npm run build 时开启以下优化&…...

理解计算机系统_线程(九):线程安全问题
前言 以<深入理解计算机系统>(以下称“本书”)内容为基础,对程序的整个过程进行梳理。本书内容对整个计算机系统做了系统性导引,每部分内容都是单独的一门课.学习深度根据自己需要来定 引入 接续理解计算机系统_线程(八):并行-CSDN博客,内容包括12.7…...

vue3基本类型和对象类型的响应式数据
vue3中基本类型和对象类型的响应式数据 OptionsAPI与CompstitionAPI的区别 OptionsAPI Options API • 特点:基于选项(options)来组织代码,将逻辑按照生命周期、数据、方法等分类。• 结构:代码按照 data 、 methods…...

3.8.4 利用RDD实现分组排行榜
本实战任务通过Spark RDD实现学生成绩的分组排行榜。首先,准备包含学生成绩的原始数据文件,并将其上传至HDFS。接着,利用Spark的交互式环境或通过创建Maven项目的方式,读取HDFS中的成绩文件生成RDD。通过map操作将数据映射为二元组…...

python web flask专题-Flask入门指南:从安装到核心功能详解
Flask入门指南:从安装到核心功能详解 Flask作为Python最流行的轻量级Web框架之一,以其简洁灵活的特性广受开发者喜爱。本文将带你从零开始学习Flask,涵盖安装配置、项目结构、应用实例、路由系统以及请求响应处理等核心知识点。 1. Flask安…...

C语言中的“类框架”工具
C语言中的“框架”:库与轻量级工具生态解析 一、C语言的设计哲学与框架定位 C语言作为一门系统级编程语言,核心目标是提供高效、灵活的底层控制能力。与Java、Python等高级语言不同,C语言本身不内置全栈框架…...

【HW系列】—web组件漏洞(Strtus2和Apache Log4j2)
本文仅用于技术研究,禁止用于非法用途。 文章目录 Struts2Struts2 框架介绍Struts2 历史漏洞汇总(表格)Struts2-045 漏洞详解 Log4j2Log4j2 框架介绍Log4j2 漏洞原理1. JNDI 注入2. 利用过程 Log4j2 历史漏洞JNDILDAP 反弹 Shell 流程 Strut…...

第六十八篇 从“超市收银系统崩溃”看JVM性能监控与故障定位实战
目录 引言:当技术问题遇上生活场景一、JVM的“超市货架管理哲学”二、收银员工具箱:JVM监控三板斧三、典型故障诊断实录四、防患于未然的运维智慧五、结语:从故障救火到体系化防控 引言:当技术问题遇上生活场景 想象一个周末的傍…...

Debian 11 之使用hostapd与dnsmasq进行AP设置
目录 1: 安装必要的软件2: 配置dnsmasq3: 配置 hostapd4: 配置网络接口5: 启动服务总结 在Debian 11(也称为Bullseye)下设置热点,你可以使用多种方法,但最常见和简单的方法之一是使用hostapd工具配合dnsmasq。这种方法不需要额外的…...

有铜半孔的设计规范与材料创新
设计关键参数 孔径与间距限制 最小孔径需≥0.6mm,孔边距≥0.5mm,避免铜层脱落;拼版时半孔区域需预留2mm间距防止撕裂。 阻焊桥设计 必须保留阻焊桥(宽度≥0.1mm),防止焊锡流入孔内造成短路。 猎板的材料…...

机器学习知识体系:从“找规律”到“做决策”的全过程解析
你可能听说过“机器学习”,觉得它很神秘,像是让电脑自己学会做事。其实,机器学习的本质很简单:通过数据来自动建立规则,从而完成预测或决策任务。 这篇文章将用通俗的语言为你梳理机器学习的知识体系,帮助…...
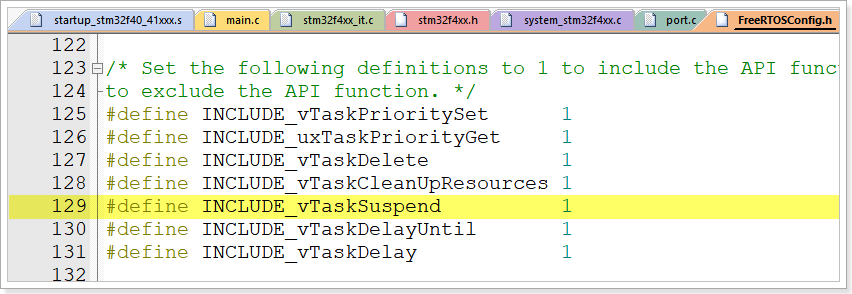
STM32之FreeRTOS移植(重点)
RTOS的基本概念 实时操作系统(Real Time Operating System)的简称就叫做RTOS,是指具有实时性、能支持实时控制系统工作的操作系统,RTOS的首要任务就是调度所有可以利用的资源来完成实时控制任务的工作,其次才是提高工…...

做好测试用例设计工作的关键是什么?
测试用例设计是软件测试的核心环节,好的测试用例能高效发现缺陷,差的测试用例则可能漏测关键问题。结合多年测试经验,我认为做好测试用例设计的关键在于以下6点: 1. 深入理解需求(核心基础) ✅ 关键点: 与产品经理/开发对齐,确保理解无偏差(避免“我以为”式测试) 拆…...

R语言科研编程-标准偏差柱状图
生成随机数据 在R中,可以使用rnorm()生成正态分布的随机数据,并模拟分组数据。以下代码生成3组(A、B、C)随机数据,每组包含10个样本: set.seed(123) # 确保可重复性 group_A <- rnorm(10, mean50, sd…...

未来教育考试答题软件4.0【自用链接备份】
未来教育考试答题软件4.0【自用链接备份】 http://www.downyi.com/downinfo/240413.html 补丁地址:https://www.wodown.com/soft/43108.html...

OpenGL Chan视频学习-11 Uniforms in OpenGL
bilibili视频链接: 【最好的OpenGL教程之一】https://www.bilibili.com/video/BV1MJ411u7Bc?p5&vd_source44b77bde056381262ee55e448b9b1973 函数网站: docs.gl 说明: 1.之后就不再单独整理网站具体函数了,网站直接翻译…...

Flink系列文章列表
把写的文章做一个汇总,会陆续更新的。 Flink流处理原理与实践:状态管理、窗口操作与容错机制-CSDN博客...

GitLab 从 17.10 到 18.0.1 的升级指南
本文分享从 GitLab 中文本 17.10.0 升级到 18.0.1 的完整过程。 升级前提 查看当前安装实例的版本。有多种方式可以查看: 方式一: /help页面 可以直接在 /help页面查看当前实例的版本。以极狐GitLab SaaS 为例,在浏览器中输入 https://ji…...

产业集群间的专利合作关系
需要准备的文件: 全国的专利表目标集群间的企业名单 根据专利的共同申请人,判断这两家企业之间存在专利合作关系。 利用1_filter_patent.py,从全国的3000多万条专利信息中,筛选出与目标集群企业相关的专利。 只要专利的申请人包…...

PyQt学习系列02-模型-视图架构与数据管理
PyQt学习系列笔记(Python Qt框架) 第二课:PyQt的模型-视图架构与数据管理 一、模型-视图架构概述 1.1 什么是模型-视图架构? 模型-视图(Model-View)是Qt框架中用于数据展示和交互的核心设计模式。它将数…...
