2025.5.23 【ZR NOI模拟赛 T3】高速公路 题解(容斥,高维前缀和,性质)
非常牛的题,记录一下思路。
传送门
题意
有一张 n n n 个点的无向图,每个点有一个颜色 c i c_i ci,满足 c i ∈ [ 1 , k ] c_i \in [1, k] ci∈[1,k]。
图是由 m m m 条链组成,满足任意一个点恰好只在一条链上。对于一条链上的第 i i i 个点和第 j j j 个点,从 i i i 沿着链走到 j j j 的花费为 ∣ i − j ∣ |i - j| ∣i−j∣。
若两个点 x , y x, y x,y 满足 c x = c y c_x = c_y cx=cy,那么可以花费 1 1 1 代价从 x x x 移动到 y y y。
定义 d i s ( x , y ) dis(x, y) dis(x,y) 为从 x x x 移动到 y y y 的最小花费。给定图的形态和每个点的颜色,求:
∑ 1 ≤ x < y ≤ n d i s ( x , y ) \sum\limits_{1 \leq x < y \leq n} dis(x, y) 1≤x<y≤n∑dis(x,y)
1 ≤ n ≤ 10 6 , 1 ≤ k ≤ 20 1 \leq n \leq 10^6, 1 \leq k \leq 20 1≤n≤106,1≤k≤20,保证所有点对都能相互到达。
分析:
由于相同颜色的点之间可以花费 1 1 1 的代价相互到达,并且颜色数很小。我们将同色的点看作同类,每次计算两类点之间的花费。
枚举 x , y x, y x,y,计算 x x x 颜色的点和 y y y 颜色的点之间的花费和:
若 x = y x = y x=y,那么答案就是 c n t x × ( c n t x − 1 ) 2 \frac{cnt_{x} \times (cnt_{x} - 1)}{2} 2cntx×(cntx−1)。其中 c n t x cnt_x cntx 表示颜色为 x x x 的点的数量。
若 x ≠ y x \ne y x=y,先来考虑如何计算两个确定的点 a , b a, b a,b 之间的花费(满足 c a = x , c b = y c_a = x, c_b = y ca=x,cb=y):
称花费 1 1 1 代价从一个点到另一个同色点为 传送。
我们发现如果最优路径下 a → b a \to b a→b 至少进行了一次传送,那么就有:
d i s ( a , b ) = min p = 1 k ( d a , p + d b , p + 1 ) dis(a, b) = \min\limits_{p = 1}^{k} (d_{a, p} + d_{b, p} + 1) dis(a,b)=p=1mink(da,p+db,p+1)
其中 d a , c d_{a, c} da,c 表示 a a a 号点到任意一个颜色为 c c c 的点的最小花费。
证明是简单的,只需要将 p p p 选成第一次传送时的颜色,然后反证法即可。
那么 d a , c d_{a, c} da,c 是好求的,只需要跑 k k k 遍 多源最短路 即可, 每次 b f s bfs bfs 总复杂度 O ( n k ) O(nk) O(nk)。
唯一存在问题的情况是 a , b a,b a,b 在同一条链上并且 a a a 只经过链上的边到达 b b b。我们先不考虑这种情况。
接下来考虑怎么整体计算两类点之间的花费:
设 D x , y D_{x, y} Dx,y 表示 任意一个颜色为 x x x 的点到达 任意一个颜色为 y y y 的点的最小花费。
那么有性质: d a , p ≤ D c a , p + 1 d_{a,p} \leq D_{c_a, p} + 1 da,p≤Dca,p+1。这是因为你可以多花费 1 1 1 的代价传送取到 D c a , p D_{c_a, p} Dca,p。
由于我们想整体计算两种颜色的贡献,因此我们将点对之间的花费 放缩 成两种颜色之间的花费:
min p = 1 k ( D x , p + D y , p + 1 ) ≤ d i s ( a , b ) ≤ min p = 1 k ( D x , p + D y , p + 1 ) + 2 \min_{p = 1}^{k}(D_{x, p} + D_{y, p} + 1) \leq dis(a, b) \leq \min\limits_{p = 1}^{k}(D_{x, p} + D_{y, p} + 1) + 2 p=1mink(Dx,p+Dy,p+1)≤dis(a,b)≤p=1mink(Dx,p+Dy,p+1)+2
设 d 1 x , y = min p = 1 k ( D x , p + D y , p + 1 ) d1_{x, y} = \min\limits_{p = 1}^{k}(D_{x, p} + D_{y, p} + 1) d1x,y=p=1mink(Dx,p+Dy,p+1)。
取值范围内只有 { d 1 x , y , d 1 x , y + 1 , d 1 x , y + 2 } \{d1_{x, y}, d1_{x, y} + 1, d1_{x, y} + 2\} {d1x,y,d1x,y+1,d1x,y+2},只需要计算有多少点对分别取到这三种值就可以算出答案。
我们来计算 d 1 x , y d1_{x, y} d1x,y 和 d 1 x , y + 2 d1_{x, y} + 2 d1x,y+2 的数量,剩下的可以用总数减去这两个得到。
设 T a T_a Ta 表示 d a , p d_{a, p} da,p 和 D c a , p D_{c_a, p} Dca,p 取等的 p p p 的集合。(一个在 [ 0 , 2 k ) [0, 2^k) [0,2k) 中的数字)
设 F x , y F_{x, y} Fx,y 表示 D x , p + D y , p + 1 D_{x, p} + D_{y, p} + 1 Dx,p+Dy,p+1 取到 d 1 x , y d1_{x, y} d1x,y 的 p p p 的集合, F x , y ′ F'_{x, y} Fx,y′ 表示取到 d 1 x , y + 1 d1_{x, y} + 1 d1x,y+1 的 p p p 的集合。
-
d i s ( a , b ) = d 1 x , y dis(a, b) = d1_{x, y} dis(a,b)=d1x,y:需要满足 T a ∩ T b ∩ F x , y ≠ ∅ T_a \cap T_b \cap F_{x, y} \ne \emptyset Ta∩Tb∩Fx,y=∅。
-
d i s ( a , b ) = d 1 x , y + 2 dis(a, b) = d1_{x, y} + 2 dis(a,b)=d1x,y+2:需要满足 T a ∩ T b ∩ F x , y ′ = ∅ T_a \cap T_b \cap F'_{x, y} = \emptyset Ta∩Tb∩Fx,y′=∅ 且 ( T a ∪ T b ) ∩ F x , y = ∅ (T_a \cup T_b) \cap F_{x, y} = \emptyset (Ta∪Tb)∩Fx,y=∅ 。
对于第一种,考虑容斥计算:拿总方案数减去交为空的方案数。对于交为空的方案数,同样是一个容斥,枚举 F x , y F_{x, y} Fx,y 的子集 S S S 钦定不合法,那么需要求出 颜色为 x x x 的点中有多少个 a a a 满足 T a T_a Ta 是 S S S 的超集,和颜色为 y y y 的点中有多少个 b b b 满足 T b T_b Tb 是 S S S 的超集。这个只需要对于每种颜色跑一遍 高维前缀和 预处理 超集和 即可。复杂度 O ( 2 k ) O(2^k) O(2k)。
对于第二种也类似:有 ∪ \cup ∪ 不好看,将限制拆成 T a ∩ F x , y = ∅ T_a \cap F_{x, y} = \emptyset Ta∩Fx,y=∅ 且 T b ∩ F x , y = ∅ T_b \cap F_{x, y} = \emptyset Tb∩Fx,y=∅。那么暴力可以写成:
∑ S 1 ⊆ F x , y ′ ∑ S 2 ⊆ F x , y ∑ S 3 ⊆ F x , y ( − 1 ) ∣ S 1 ∣ + ∣ S 2 ∣ + ∣ S 3 ∣ × h x , S 1 ∪ S 2 × h y , S 1 ∪ S 3 \sum\limits_{S_1 \subseteq F'_{x, y}}\sum\limits_{S_2 \subseteq F_{x, y}}\sum\limits_{S_3 \subseteq F_{x, y}}(-1)^{|S_1| + |S_2| + |S_3|} \times h_{x, S_1 \cup S_2} \times h_{y, S1 \cup S_3} S1⊆Fx,y′∑S2⊆Fx,y∑S3⊆Fx,y∑(−1)∣S1∣+∣S2∣+∣S3∣×hx,S1∪S2×hy,S1∪S3
其中 h a , S h_{a, S} ha,S 是求出的超集和数组。
那么可以写成:
∑ S 1 ⊆ F x , y ′ ( − 1 ) ∣ S 1 ∣ ( ∑ S 2 ⊆ F x , y ( − 1 ) ∣ S 2 ∣ × h x , S 1 ∪ S 2 ) ( ∑ S 3 ⊆ F x , y ( − 1 ) ∣ S 3 ∣ × h y , S 1 ∪ S 3 ) \sum\limits_{S_1 \subseteq F'_{x, y}} (-1)^{|S_1|} (\sum\limits_{S_2 \subseteq F_{x, y}} (-1)^{|S_2|} \times h_{x, S_1 \cup S_2}) (\sum\limits_{S_3 \subseteq F_{x, y}}(-1)^{|S_3|} \times h_{y, S1 \cup S_3}) S1⊆Fx,y′∑(−1)∣S1∣(S2⊆Fx,y∑(−1)∣S2∣×hx,S1∪S2)(S3⊆Fx,y∑(−1)∣S3∣×hy,S1∪S3)
那么枚举 S 1 S_1 S1 后, S 2 , S 3 S_2, S_3 S2,S3 的枚举就独立了。注意到 ∣ F x , y ′ ∣ + ∣ F x , y ∣ ≤ k |F'_{x, y}| + |F_{x, y}| \leq k ∣Fx,y′∣+∣Fx,y∣≤k,因此复杂度还是 O ( 2 k ) O(2^k) O(2k)。
还剩下最开始的一个问题:同一条链上的点对这样求可能不对,怎么改成对的?
我们发现任意两个点之间花费不会超过 2 k 2k 2k。这是因为如果将最优路径的点的颜色依次写下来,如果存在一种颜色出现次数 ≥ 3 \geq 3 ≥3,那么显然可以调整为更优。因此每种颜色不会出现超过 2 2 2 次。
那么就枚举每一条链上距离不超过 2 k 2k 2k 的点对,先将它们在整体计算时的贡献撤销,然后算出正确答案加进来即可。枚举量为 O ( n k ) O(nk) O(nk)。
总复杂度就是 O ( n k + k 2 2 k ) O(nk + k^22^k) O(nk+k22k)。
CODE:
// 核心思路是根据 k 比较小想到将不同颜色的两类点整体算它们之间的贡献
// 需要处理:每个点到某种颜色的最小距离, 每种颜色到其它颜色的最小值
#include<bits/stdc++.h>
#define pb emplace_back
using namespace std;
typedef long long LL;
const int N = 1e6 + 50;
const int M = 31;
unordered_map< int, int > cm[M];
int n, m, K, idx[500], rk, nc, node[M], col[N];
int dis[M][N], d[M][M], d1[M][M], Dis[N];
int Cnt[M][1 << 20], T[N], S[M][M], S_[M][M];
LL res;
string r[N];
vector< int > cnd[M];
struct edge {int v, last, w;
} E[N * 4];
int tot, head[N];
inline void add(int u, int v, int w) {E[++ tot] = (edge) {v, head[u], w};head[u] = tot;
}
bool vis[N];
inline void bfs(int c) {deque< int > q; memset(dis[c], 0x3f, sizeof dis[c]); for(auto v : cnd[c]) dis[c][v] = 0, q.push_back(v);while(!q.empty()) {int u = q.front(); q.pop_front(); for(int i = head[u]; i; i = E[i].last) {int v = E[i].v; if(dis[c][v] > dis[c][u] + E[i].w) {dis[c][v] = dis[c][u] + E[i].w;if(!E[i].w) q.push_front(v);else q.push_back(v);}}}for(int i = 1; i <= nc; i ++ ) if(col[i]) d[c][col[i]] = min(d[c][col[i]], dis[c][i]);
}
inline void fwt(int *f) {for(int i = 0; i < K; i ++ ) for(int s = 0; s < (1 << K); s ++ ) if((s >> i & 1)) f[s ^ (1 << i)] += f[s];
}
inline int get(int x, int y) { // 在不考虑同一条链下 (x, y) 之间的答案 if(col[x] == col[y]) return 1;else if((T[x] & T[y] & S[col[x]][col[y]]) != 0) return d1[col[x]][col[y]];else if(((T[x] | T[y]) & S[col[x]][col[y]]) == 0 && (T[x] & T[y] & S_[col[x]][col[y]]) == 0) return d1[col[x]][col[y]] + 2;else return d1[col[x]][col[y]] + 1;
}
inline int sz(int x) {return __builtin_popcount(x);}
inline int sign(int x) {return (x & 1) ? -1 : 1;}
inline LL calc(int x, int y) { // x, y 两种颜色的贡献 if(x == y) {int cnt = cnd[x].size(); return 1LL * cnt * (cnt - 1) / 2;}if(K <= 20) { // 首先计算答案是 d1[x][y]的点对数量 int cx = cnd[x].size(), cy = cnd[y].size();LL res = 0, rest = 0;for(int ts = S[x][y]; ; ts = (ts - 1 & S[x][y])) {rest = rest + 1LL * Cnt[x][ts] * Cnt[y][ts] * sign(sz(ts));if(!ts) break;}res += (1LL * cx * cy - rest) * d1[x][y];// 接着计算有多少是 d1[x][y] + 2 LL num = 0;for(int ts1 = S_[x][y]; ; ts1 = (ts1 - 1 & S_[x][y])) { // 容斥两次 LL rx = 0, ry = 0;for(int ts2 = S[x][y]; ; ts2 = (ts2 - 1 & S[x][y])) {rx += 1LL * Cnt[x][ts1 | ts2] * sign(sz(ts2));ry += 1LL * Cnt[y][ts1 | ts2] * sign(sz(ts2));if(!ts2) break;}num += rx * ry * sign(sz(ts1));if(!ts1) break;}res += num * (d1[x][y] + 2);rest -= num;res += rest * (d1[x][y] + 1);return res;}else {LL res = 0;for(auto u : cm[x]) for(auto v : cm[y]) {LL c1 = u.second, c2 = v.second;int tx = u.first, ty = v.first;if((tx & ty & S[x][y]) != 0) res += c1 * c2 * d1[x][y];else if((tx & ty & S_[x][y]) == 0 && ((tx | ty) & S[x][y]) == 0) res += c1 * c2 * (d1[x][y] + 2);else res += c1 * c2 * (d1[x][y] + 1);}return res;}
}
int main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);cin >> n >> m >> K;memset(d, 0x3f, sizeof d);for(int i = 1; i <= K; i ++ ) node[i] = ++ nc;for(int i = 1; i <= m; i ++ ) {cin >> r[i];for(int j = 0; j < r[i].size(); j ++ ) {if(!idx[r[i][j]]) idx[r[i][j]] = ++ rk;nc ++; col[nc] = idx[r[i][j]]; cnd[col[nc]].pb(nc);add(nc, node[col[nc]], 0); add(node[col[nc]], nc, 1);if(j) add(nc, nc - 1, 1), add(nc - 1, nc, 1);}}for(int i = 1; i <= K; i ++ ) bfs(i);for(int i = 1; i <= K; i ++ ) {for(int j = 1; j <= K; j ++ ) {d1[i][j] = 1e8;for(int k = 1; k <= K; k ++ ) {d1[i][j] = min(d1[i][j], d[i][k] + d[j][k] + 1);}for(int k = 1; k <= K; k ++ ) {if(d[i][k] + d[j][k] + 1 == d1[i][j]) S[i][j] |= (1 << k - 1);else if(d[i][k] + d[j][k] + 1 == d1[i][j] + 1) S_[i][j] |= (1 << k - 1);}}}for(int i = 1; i <= K; i ++ ) {for(auto v : cnd[i]) {int S = 0;for(int j = 1; j <= K; j ++ ) if(dis[j][v] == d[i][j]) S |= (1 << j - 1);if(K <= 20) Cnt[i][S] ++;else cm[i][S] ++;T[v] = S;}if(K <= 20) fwt(Cnt[i]); // 超集贡献 }for(int i = 1; i <= K; i ++ ) for(int j = i; j <= K; j ++ ) res += calc(i, j);int id = K;for(int i = 1; i <= m; i ++ ) { // 计算同一条链上的贡献。 答案不超过 2 * K int len = r[i].size() - 1;for(int j = 0; j <= len; j ++ ) {for(int k = 1; k <= 2 * K && j + k <= len; k ++ ) {res = res - get(id + j + 1, id + j + k + 1) + min(get(id + j + 1, id + j + k + 1), k);}}id += len + 1;}cout << res << endl;return 0;
}
相关文章:
)
2025.5.23 【ZR NOI模拟赛 T3】高速公路 题解(容斥,高维前缀和,性质)
非常牛的题,记录一下思路。 传送门 题意 有一张 n n n 个点的无向图,每个点有一个颜色 c i c_i ci,满足 c i ∈ [ 1 , k ] c_i \in [1, k] ci∈[1,k]。 图是由 m m m 条链组成,满足任意一个点恰好只在一条链上。对于一…...

QGIS新手教程2:线图层与多边形图层基础操作指南(点线互转、中心点提取与WKT导出)
QGIS新手教程:线图层与多边形图层基础操作指南(点线互转、中心点提取与WKT导出) 目录 QGIS新手教程:线图层与多边形图层基础操作指南(点线互转、中心点提取与WKT导出)📌 引言第一部分࿱…...

nova14 ultra,是如何防住80°C热水和10000KPa水压冲击的?
暴雨突袭,手忙脚乱护住背包,却担心手机被雨水浸湿;泳池里想记录美好时刻,却担心手机掉入水中 ;厨房里充满了高温水汽,近距离拍摄美食瞬间,手机屏幕花屏,让人失去了对美食的兴趣…… …...
完整指南)
Spring Boot项目中实现单点登录(SSO)完整指南
单点登录(Single Sign-On, SSO)是一种身份验证机制,允许用户使用一组凭证(如用户名和密码)登录多个相关但独立的系统。 一、单点登录的核心原理 SSO的核心原理使集中认证、分散授权,主要流程如下: 1.用户访问应用A 2.应用A检查本地会话&a…...

Windows环境下Redis的安装使用与报错解决
最近在做项目的时候需要用到Redis,本来没觉得是什么麻烦,下载安装使用一步到位的事,但紧随而来的问题,让我开始怀疑人生,再加上代码跑不出来,我还专门找人给我看看怎么个是,结果就是单纯的Redis…...

鸿蒙完整项目-仿盒马App(一)首页静态页面
跟着鸿蒙小林博主,练习下项目~记录下首页的搭建,后续继续完善和整体项目完成会进行布局修改,先按照博主的跟做,后续在改 1.分为底部整体框架搭建 2.首页布局(顶部搜索、新人专享、金刚区(两个不同集合数据)…...
——Agent(基于大型语言模型的智能代理))
大模型(4)——Agent(基于大型语言模型的智能代理)
大模型Agent是一种基于大型语言模型(LLM)的智能系统,能够自主感知环境、规划任务、调用工具并完成复杂目标。其核心原理是将大模型的推理能力与外部行动能力结合,实现从“思考”到“行动”的闭环。以下是其原理详解与实现方法&…...
39-居住证管理系统(小程序)
技术栈: springBootVueMysqlUni-app 功能点: 群众端 警方端 管理员端 群众端: 1.首页: 轮播图展示、公告信息列表 2.公告栏: 公告查看及评论 3.我的: 联系我们: 可在线咨询管理员问题 实时回复 居住证登记申请 回执单查看 领证信息查看 4.个人中心: 个人信息查看及修改…...

WPF【11_4】WPF实战-重构与美化(MVVM 架构)
11-9 【理论】MVVM 架构 在 WPF 项目中,我们主要采用的是一种类似 MVC 的架构,叫做 MVVM。 MVVM 继承了 MVC 的理念,是 Model-View-ViewModel 的缩写,中文意思是模型、视图、视图模型。这三个词分开看我们都能看懂,不…...

计算逆时针夹角(有向角度)——CAD c# 实现两条线(向量)的逆时针夹角
效果如下: 附部分代码如下: public void 逆时针夹角Demo(){// 获取当前 CAD 文档和编辑器Document doc Application.DocumentManager.MdiActiveDocument;Editor ed doc.Editor;Database db doc.Database;try{Point3d vec1Start, vec1End;if (!GetTwoP…...

鸿蒙OSUniApp 开发带有通知提示的功能组件#三方框架 #Uniapp
使用 UniApp 开发带有通知提示的功能组件 在移动应用开发中,通知提示(Notification/Toast/Alert)是提升用户体验和交互效率的重要手段。无论是表单校验、操作反馈、系统消息还是营销推送,合理的通知提示都能帮助用户及时获取关键…...

前端EXCEL插件智表ZCELL数据源功能详解
一、数据源功能介绍 前端EXCEL插件智表ZCELL提供了强大的数据源管理功能,使开发者能够灵活地在电子表格中集成和管理结构化数据。数据源功能主要分为两种类型: 卡片式数据源:适合展示和编辑单个数据记录 表格式数据源:适合处理表…...

打卡第31天:模块和库的导入
重复内容 知识点回顾: 1.导入官方库的三种手段 2.导入自定义库/模块的方式 3.导入库/模块的核心逻辑:找到根目录(python解释器的目录和终端的目录不一致) 作业:自己新建几个不同路径文件尝试下如何导入 导入机制的核…...

LLM Coding
AI Coding 深度解析:探索编程新范式与未来趋势 | w3cschool笔记https://www.phodal.com/blog/ai-friendly-architecture/bmadcode/BMAD-METHOD: Breakthrough Method for Agile Ai Driven Development...

Qt 的多线程
Qt 中的多线程主要用于处理耗时操作,避免阻塞主线程(UI 线程),从而提高程序的响应性和运行效率。以下是 Qt 多线程的相关技术总结: 常见的多线程实现方式 继承 QThread 类 :最基础的实现方式,具体步骤为继承 QThread 类,重写其 run() 函数,在 run() 函数中编写线程要…...

【请关注】各类MySQL数据备份还原分享
MySQL数据备份的全部方法 MySQL数据备份是数据库管理中的关键任务,以下是MySQL数据备份的全面方法总结: 一、逻辑备份方法 1. **mysqldump工具** - 最常用的备份工具 - 命令示例: >bash mysqldump -u [username] -p[password] [database_name] > backup.sql > -…...

Go语言方法与接收者 -《Go语言实战指南》
在 Go 中,方法是绑定到某个类型上的函数。与普通函数不同,方法具有一个“接收者(receiver)”,用于指定它是哪个类型的“方法”。 一、方法的定义语法 func (接收者名 接收者类型) 方法名(参数列表) 返回值列表 {// 方…...

基于 STM32 的农村污水处理控制系统设计与实现
摘要 针对农村污水处理自动化程度低、运维成本高的问题,本文设计了一种基于 STM32 单片机的污水处理控制系统。系统通过多传感器实时监测水质参数,结合 PID 控制算法实现污水处理全流程自动化,并集成远程监控功能,满足农村地区低成本、易维护的需求。 一、硬件系统设计 …...

【Linux】进程 信号的产生
🌻个人主页:路飞雪吖~ 🌠专栏:Linux 目录 一、掌握Linux信号的基本概念 🌠前台进程 VS 后台进程 🌠 小贴士: 🪄⼀个系统函数 --- signal() 🪄查看信号 --- man 7 sign…...

实时操作系统革命:实时Linux驱动的智能时代底层重构
一、智能时代对实时性的终极挑战 在万物互联的智能时代,人类对机器响应速度的期待已突破物理极限。当工业机器人以亚毫米级精度执行微米级加工任务,当自动驾驶系统在130公里时速下需在10毫秒内完成决策切换,当医疗机器人需在5毫秒内响应神经…...

NGINX HTTP/3 实验指南安装、配置与调优
一、HTTP/3 简介 基于 QUIC:在 UDP 之上实现的多路复用传输,内置拥塞控制与前向纠错,无需三次握手即可恢复连接。零 RTT 重连:借助 TLS 1.3,实现连接恢复时的 0-RTT 数据发送(视底层库支持)。多…...

机器学习中的维度、过拟合、降维
1. 维度灾难 当我们谈论机器学习模型在处理数据时遇到的困难,一个常常被提及的词便是“维度灾难”(Curse of Dimensionality)。这不是科幻小说里的情节,而是数学和计算世界里真实存在的困境。它指的正是:当数据集的特…...

关于git的使用
下载git 可以去git的官网下载https://git-scm.com/downloads 也可以去找第三方的资源下载,下载后是一个exe应用程序,直接点开一直下一步就可以安装了 右键任意位置显示这两个就代表成功,第一个是git官方的图形化界面,第二个是用…...

预约按摩小程序源码介绍
基于ThinkPHP、FastAdmin和UniApp开发的预约按摩小程序源码,ThinkPHP作为后端框架,以其高效稳定著称,能妥善处理数据逻辑与业务规则。FastAdmin作为后台管理框架,极大简化了后台管理系统的搭建与维护。UniApp则让小程序具备跨平台…...

Elasticsearch创建快照仓库报错处理
创建快照仓库报错: 根据报错提示的信息,问题可能出在 Elasticsearch 的配置中。当你尝试创建一个文件系统(fs)类型的快照仓库时,虽然已经指定了 location 参数,但 Elasticsearch 仍然报错,这通…...

LINUX安装运行jeelowcode前端项目
参考 JeeLowCode低代码社区,JeeLowCode低代码开发平台,JeeLowCode低代码开发框架,快速启动(VUE) 安装node 18 LINUX安装node/nodejs_linux安装node 安装到哪-CSDN博客 安装PNPM LINUX安装PNPM-CSDN博客 下载 git clone https://gitcode.com/jeelo…...
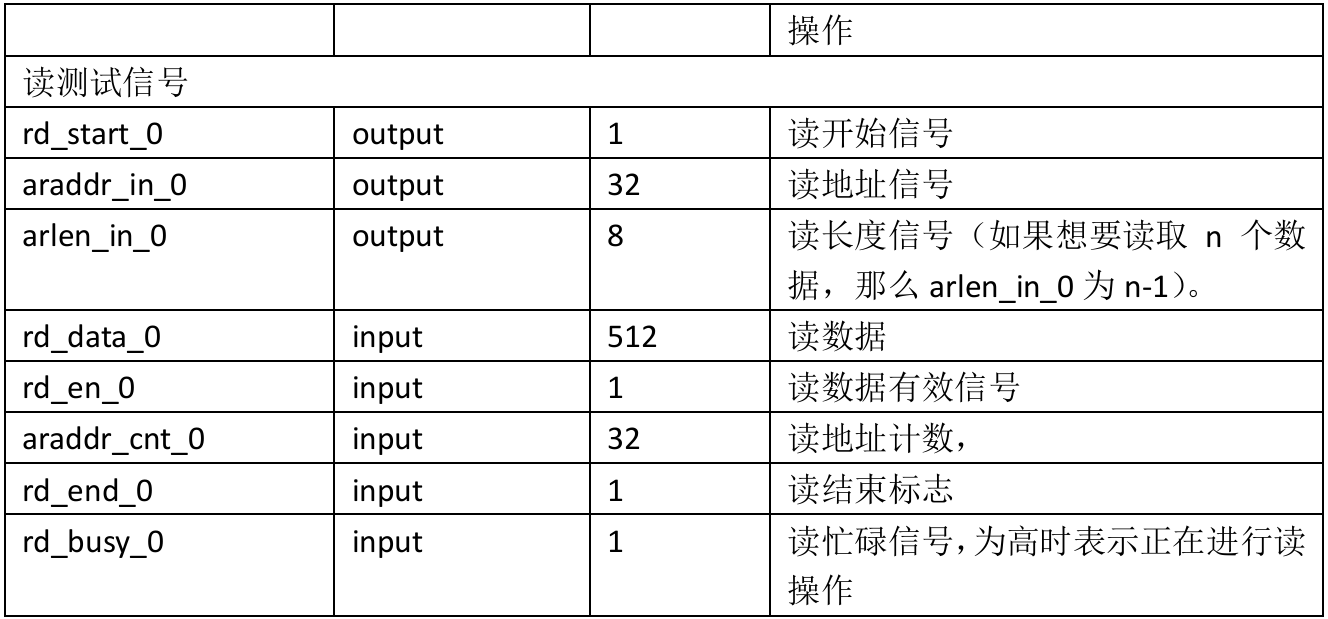
使用DDR4控制器实现多通道数据读写(十三)
一、概述 在上一章节中使用仿真简单验证了interconnect的功能,使用四个axi4的主端口同时发起读写命令,经过interconnect后,将这些读写指令依次发给ddr4控制器。Ddr4控制器响应后再依次将响应发送到各个通道。从而实现多通道读写ddr4控制器的功…...

如何描述BUG
一、如何描述BUG 1.1 版本信息 1.1.1 必填项 精确到构建版本号(如v2.3.1_build20240615) 获取方式: 代码版本控制系统(Git提交哈希值)应用内版本信息(App的About页面)持续集成工具生成的版本…...

Python进阶:如何通过组合模式实现高性能Vector类?
🔍 设计动机:为何抛弃继承选择组合? 在实现多维向量类Vector时,我们刻意采用组合模式而非继承,核心优势在于: 高扩展性:通过array数组存储分量,天然支持高维向量低耦合:…...

谷歌Veo vs Sora:AI视频生成技术的巅峰对决
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 ——从架构到实践,解析音画同步、物理模拟与长视频生成的破局之战 一、技术架构:双雄对垒,殊途同归? 谷歌…...
