拓扑排序算法剖析与py/cpp/Java语言实现
拓扑排序算法深度剖析与py/cpp/Java语言实现
- 一、拓扑排序算法的基本概念
- 1.1 有向无环图(DAG)
- 1.2 拓扑排序的定义
- 1.3 拓扑排序的性质
- 二、拓扑排序算法的原理与流程
- 2.1 核心原理
- 2.2 算法流程
- 三、拓扑排序算法的代码实现
- 3.1 Python实现
- 3.2 C++实现
- 3.3 Java实现
- 四、拓扑排序算法的时间复杂度与空间复杂度分析
- 4.1 时间复杂度
- 4.2 空间复杂度
- 五、拓扑排序算法的应用场景
- 5.1 任务调度
- 5.2 课程安排
- 5.3 软件模块依赖管理
- 5.4 事件驱动系统
- 总结
图论中,拓扑排序(Topological Sorting)以其独特的性质和广泛的应用场景,成为处理有向无环图(Directed Acyclic Graph,DAG)问题的重要工具。无论是任务调度、课程安排,还是软件项目的模块依赖管理,拓扑排序都发挥着关键作用。本文我将深入剖析拓扑排序算法的基本概念、原理、实现方式,并使用Python、C++和Java三种语言进行代码实现,带你全面掌握这一经典算法。
一、拓扑排序算法的基本概念
1.1 有向无环图(DAG)
在理解拓扑排序之前,首先需要明确有向无环图的概念。有向图是指图中的边具有方向的图,而无环图则是指图中不存在回路(环)的图。有向无环图结合了这两个特性,它由顶点集合 (V) 和有向边集合 (E) 组成,且图中不存在任何路径能够从一个顶点出发,经过若干条边后又回到该顶点。有向无环图常用于表示具有先后顺序或依赖关系的系统,例如任务之间的执行顺序、课程之间的先修关系等。
1.2 拓扑排序的定义
对于一个有向无环图 (G=(V, E)),拓扑排序是将图中的所有顶点排成一个线性序列,使得对于图中的任意一条有向边 ((u, v)),在该线性序列中,顶点 (u) 都排在顶点 (v) 的前面。简单来说,拓扑排序的结果是一个满足所有边的方向约束的顶点序列,它反映了图中顶点之间的依赖关系。例如,在课程安排中,若课程 (A) 是课程 (B) 的先修课程,那么在拓扑排序后的序列中,课程 (A) 必然排在课程 (B) 之前 。
1.3 拓扑排序的性质
- 唯一性:一个有向无环图的拓扑排序结果不一定唯一。如果图中存在多个没有前驱(入度为 0)的顶点,那么在排序过程中,这些顶点的相对顺序可以任意排列,从而导致不同的拓扑排序结果。
- 存在性:只有有向无环图才有拓扑排序。如果图中存在环,那么必然无法找到一个满足所有边方向约束的线性序列,因为环中的顶点会形成相互依赖的关系,无法确定先后顺序。
二、拓扑排序算法的原理与流程
2.1 核心原理
拓扑排序算法基于有向无环图的性质,通过不断选择入度为 0 的顶点,并将其从图中移除,同时更新剩余顶点的入度,逐步构建出拓扑排序序列。入度是指指向某个顶点的边的数量,入度为 0 的顶点表示没有其他顶点依赖于它,因此可以首先将其加入拓扑排序序列。移除该顶点后,与它相连的边也会被移除,这会导致其他顶点的入度发生变化,继续寻找新的入度为 0 的顶点,重复这个过程,直到图中所有顶点都被处理完毕。
2.2 算法流程
- 初始化:统计图中每个顶点的入度,并将入度为 0 的顶点放入一个队列(或栈)中。同时,创建一个用于存储拓扑排序结果的列表。
- 处理顶点:从队列(或栈)中取出一个入度为 0 的顶点,将其加入拓扑排序结果列表中。然后遍历该顶点的所有出边,对于每条出边 ((u, v)),将顶点 (v) 的入度减 1。如果顶点 (v) 的入度变为 0,则将其放入队列(或栈)中。
- 重复步骤:不断重复步骤 2,直到队列(或栈)为空。此时,如果拓扑排序结果列表中的顶点数量等于图中顶点的总数,说明拓扑排序成功;否则,说明图中存在环,无法进行拓扑排序。

三、拓扑排序算法的代码实现
3.1 Python实现
from collections import dequedef topological_sort(graph):in_degree = {v: 0 for v in graph}for vertex in graph:for neighbor in graph[vertex]:in_degree[neighbor] += 1queue = deque([v for v in in_degree if in_degree[v] == 0])result = []while queue:vertex = queue.popleft()result.append(vertex)for neighbor in graph[vertex]:in_degree[neighbor] -= 1if in_degree[neighbor] == 0:queue.append(neighbor)if len(result) == len(graph):return resultelse:raise ValueError("图中存在环,无法进行拓扑排序")# 示例图,使用字典表示邻接表
graph = {'A': ['B', 'C'],'B': ['D'],'C': ['D'],'D': []
}
print(topological_sort(graph))
在上述Python代码中,首先通过遍历图统计每个顶点的入度,将入度为 0 的顶点加入队列。然后在循环中不断取出队列中的顶点,更新其邻居顶点的入度,将新的入度为 0 的顶点加入队列,最后判断结果列表的长度是否与图的顶点数相等,以确定是否成功完成拓扑排序。
3.2 C++实现
#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>
using namespace std;vector<string> topologicalSort(unordered_map<string, vector<string>>& graph) {unordered_map<string, int> inDegree;for (auto& vertex : graph) {inDegree[vertex.first] = 0;}for (auto& vertex : graph) {for (string neighbor : vertex.second) {inDegree[neighbor]++;}}queue<string> q;for (auto& entry : inDegree) {if (entry.second == 0) {q.push(entry.first);}}vector<string> result;while (!q.empty()) {string vertex = q.front();q.pop();result.push_back(vertex);for (string neighbor : graph[vertex]) {inDegree[neighbor]--;if (inDegree[neighbor] == 0) {q.push(neighbor);}}}if (result.size() == graph.size()) {return result;} else {throw invalid_argument("图中存在环,无法进行拓扑排序");}
}int main() {unordered_map<string, vector<string>> graph = {{"A", {"B", "C"}},{"B", {"D"}},{"C", {"D"}},{"D", {}}};try {vector<string> sorted = topologicalSort(graph);for (string vertex : sorted) {cout << vertex << " ";}} catch (const invalid_argument& e) {cout << e.what() << endl;}return 0;
}
C++代码中,使用unordered_map来存储图的邻接表和顶点的入度信息。通过两次遍历图统计入度,将入度为 0 的顶点入队。在循环处理队列顶点的过程中,更新邻居顶点入度并判断是否入队,最后根据结果列表长度判断拓扑排序是否成功。
3.3 Java实现
import java.util.*;public class TopologicalSort {public static List<String> topologicalSort(Map<String, List<String>> graph) {Map<String, Integer> inDegree = new HashMap<>();for (String vertex : graph.keySet()) {inDegree.put(vertex, 0);}for (List<String> neighbors : graph.values()) {for (String neighbor : neighbors) {inDegree.put(neighbor, inDegree.getOrDefault(neighbor, 0) + 1);}}Queue<String> queue = new LinkedList<>();for (Map.Entry<String, Integer> entry : inDegree.entrySet()) {if (entry.getValue() == 0) {queue.offer(entry.getKey());}}List<String> result = new ArrayList<>();while (!queue.isEmpty()) {String vertex = queue.poll();result.add(vertex);List<String> neighbors = graph.get(vertex);if (neighbors != null) {for (String neighbor : neighbors) {inDegree.put(neighbor, inDegree.get(neighbor) - 1);if (inDegree.get(neighbor) == 0) {queue.offer(neighbor);}}}}if (result.size() == graph.size()) {return result;} else {throw new IllegalArgumentException("图中存在环,无法进行拓扑排序");}}public static void main(String[] args) {Map<String, List<String>> graph = new HashMap<>();graph.put("A", Arrays.asList("B", "C"));graph.put("B", Arrays.asList("D"));graph.put("C", Arrays.asList("D"));graph.put("D", Collections.emptyList());try {List<String> sorted = topologicalSort(graph);for (String vertex : sorted) {System.out.print(vertex + " ");}} catch (IllegalArgumentException e) {System.out.println(e.getMessage());}}
}
Java代码利用HashMap存储图和顶点入度,LinkedList作为队列。通过遍历图统计入度,将入度为 0 的顶点入队。在循环处理队列元素时,更新邻居顶点入度并判断入队情况,最后根据结果列表长度判断拓扑排序是否可行。
四、拓扑排序算法的时间复杂度与空间复杂度分析
4.1 时间复杂度
拓扑排序算法的时间复杂度主要由两部分组成:
- 统计每个顶点入度的时间复杂度:需要遍历图中的所有边,假设图中有 (V) 个顶点和 (E) 条边,遍历边的操作时间复杂度为 (O(E))。同时,在统计入度过程中对每个顶点的操作时间复杂度为 (O(V)),因此统计入度的总时间复杂度为 (O(V + E))。
- 处理顶点和更新入度的时间复杂度:在处理顶点的循环中,每个顶点最多被访问一次,每条边也最多被访问一次,所以处理顶点和更新入度的时间复杂度同样为 (O(V + E))。
综合以上两部分,拓扑排序算法的时间复杂度为 (O(V + E)),其中 (V) 是顶点的数量,(E) 是边的数量。
4.2 空间复杂度
拓扑排序算法的空间复杂度主要取决于存储图的结构、入度信息以及队列(或栈)所需的空间:
- 存储图的结构:如果使用邻接表存储图,空间复杂度为 (O(V + E));如果使用邻接矩阵存储图,空间复杂度为 (O(V^2))。通常情况下,邻接表更适合存储稀疏图,空间效率更高。
- 存储入度信息:需要一个数组或哈希表来存储每个顶点的入度,空间复杂度为 (O(V))。
- 队列(或栈):在最坏情况下,队列(或栈)中可能存储所有顶点,空间复杂度为 (O(V))。
综合起来,拓扑排序算法的空间复杂度为 (O(V + E))(使用邻接表存储图时) 。
五、拓扑排序算法的应用场景
5.1 任务调度
在项目管理中,一个项目通常包含多个任务,这些任务之间可能存在依赖关系,例如任务 (B) 必须在任务 (A) 完成后才能开始。将任务看作顶点,任务之间的依赖关系看作有向边,通过拓扑排序可以得到一个合理的任务执行顺序,确保在执行某个任务时,其依赖的任务已经完成。例如,在软件开发项目中,编写测试代码需要在功能代码完成之后,通过拓扑排序可以规划出各个模块开发和测试的先后顺序,提高项目开发效率。
5.2 课程安排
在大学课程体系中,许多课程存在先修关系,比如学习高级数据结构课程需要先修完基础数据结构课程。将课程看作顶点,先修关系看作有向边,利用拓扑排序可以生成一个满足所有先修条件的课程学习顺序,帮助学生合理安排学习计划 。
5.3 软件模块依赖管理
在大型软件系统中,不同的软件模块之间可能存在依赖关系,例如模块 (A) 使用了模块 (B) 提供的功能,那么模块 (A) 依赖于模块 (B)。通过拓扑排序可以确定软件模块的编译和链接顺序,确保在编译某个模块时,其依赖的模块已经编译完成,避免出现链接错误。
5.4 事件驱动系统
在事件驱动的系统中,事件之间可能存在先后顺序,例如事件 (B) 必须在事件 (A) 触发之后才能触发。将事件看作顶点,事件之间的触发关系看作有向边,拓扑排序可以确定事件的触发顺序,保证系统按照正确的逻辑运行。
总结
拓扑排序算法是处理有向无环图的重要工具,通过本文对拓扑排序算法的基本概念、原理流程、三种语言实现、复杂度分析以及应用场景的详细介绍,相信你对该算法已经有了全面而深入的理解。无论是项目管理、课程规划,还是软件开发场景中,拓扑排序算法都能为我们提供有效的解决方案。
That’s all, thanks for reading!
觉得有用就点个赞、收进收藏夹吧!关注我,获取更多干货~
相关文章:

拓扑排序算法剖析与py/cpp/Java语言实现
拓扑排序算法深度剖析与py/cpp/Java语言实现 一、拓扑排序算法的基本概念1.1 有向无环图(DAG)1.2 拓扑排序的定义1.3 拓扑排序的性质 二、拓扑排序算法的原理与流程2.1 核心原理2.2 算法流程 三、拓扑排序算法的代码实现3.1 Python实现3.2 C实现3.3 Java…...

罗马-华为
SPA应用:single-page application:单页应用SPA是一种网络应用程序或网站的模型,它通过动态重写当前页面来与用户交互,这种方法避免了页面之间切换打断用户体验在单页应用中 集成 ROMA Connect 主要包含四个组件:数据集成( FDI )、服务集成( APIC )、消息集成 ( MQS …...

单例模式的隐秘危机
引言 单例模式作为设计模式中的基石,广泛应用于配置管理、线程池、缓存系统等关键场景。然而,许多开发者误以为“私有构造函数”足以保障其唯一性,却忽视了反射机制、对象克隆、序列化反序列化这三把“隐形利刃”——它们能绕过常规防御&…...

微信小程序常用方法
微信小程序 常用方法 setData() https://developers.weixin.qq.com/miniprogram/dev/reference/api/Page.html#%E7%BB%84%E4%BB%B6%E4%BA%8B%E4%BB%B6%E5%A4%84%E7%90%86%E5%87%BD%E6%95%B0 在微信小程序中,setData 是一个非常重要的方法,主要用于更新…...
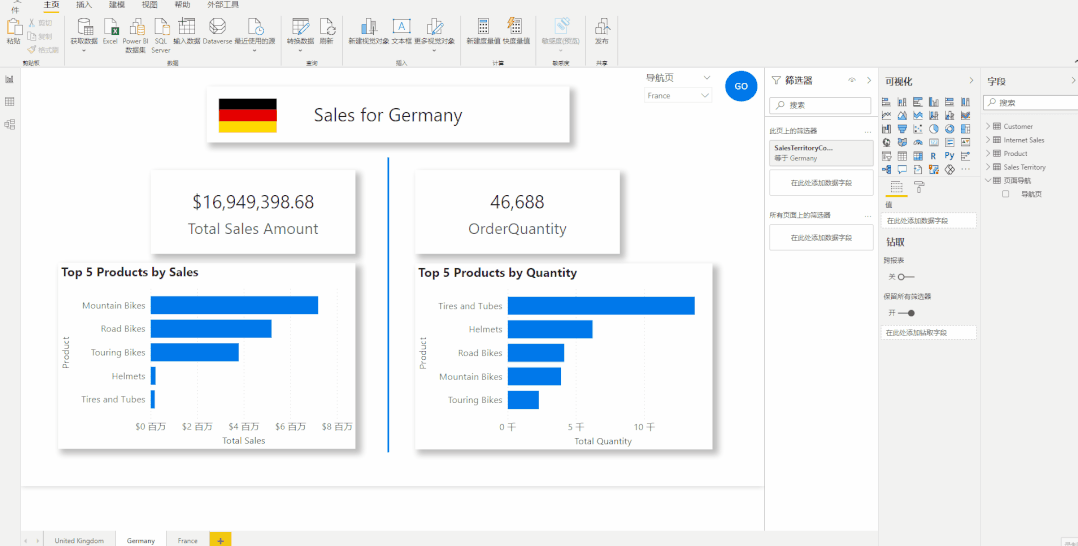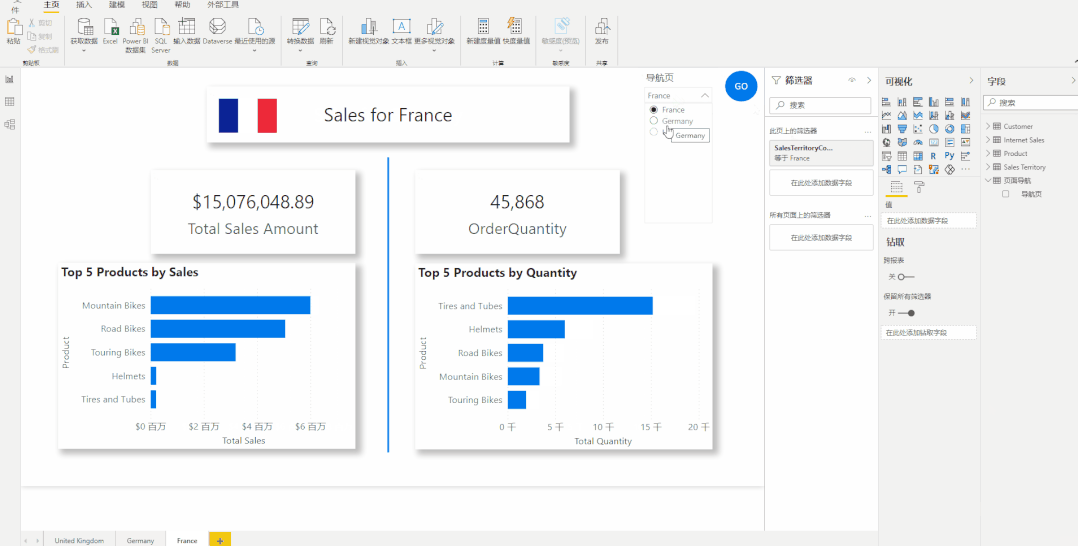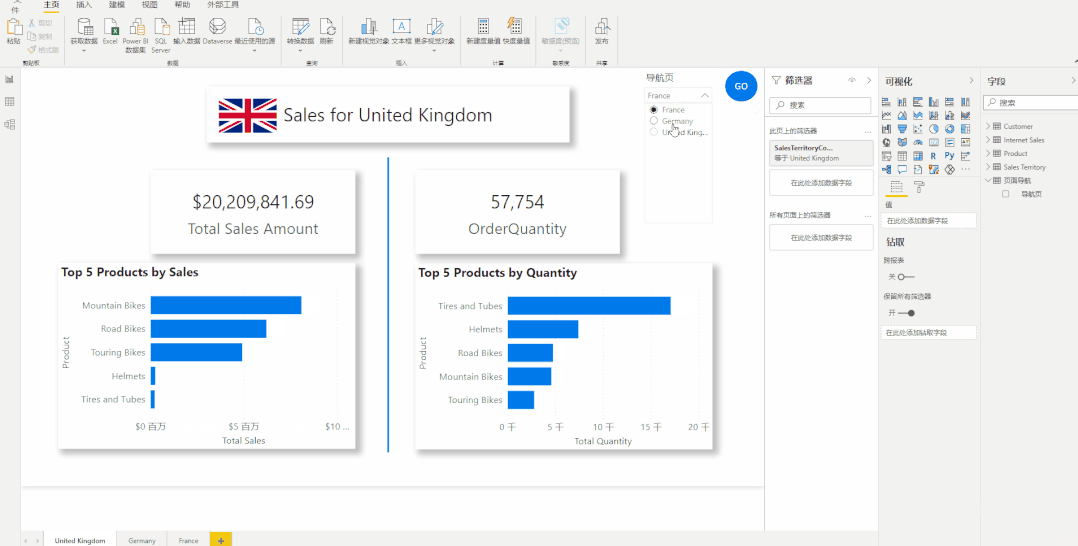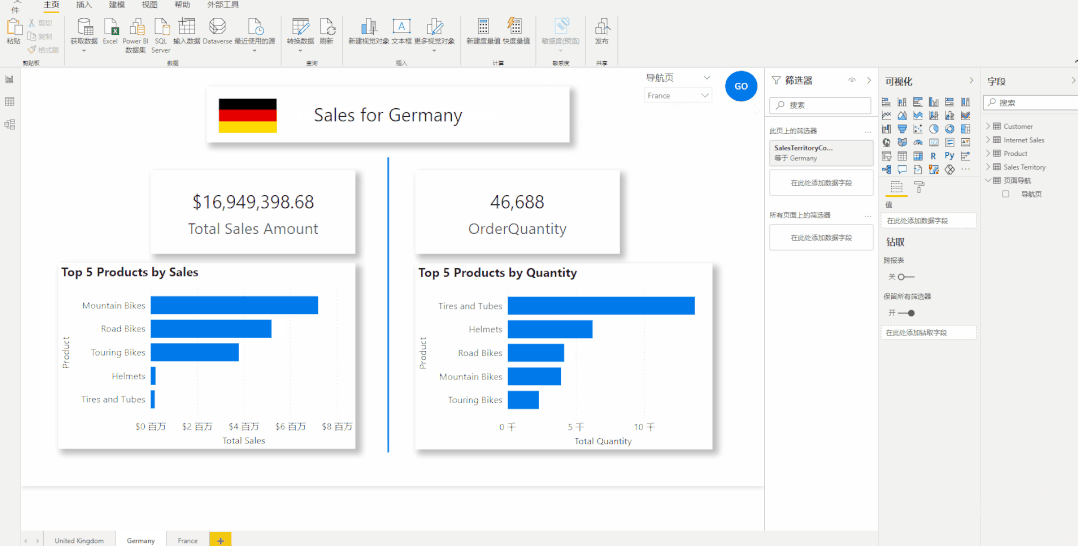
切片器导航-大量报告页查看的更好方式
切片器导航-大量报告页查看的更好方式 现在很多报告使用的是按钮导航,即使用书签按钮来制作页面导航的方式。但是当我们的报告有几十页甚至上百页的时候,使用书签按钮来制作页面导航,无论是对于报表制作者还是报告使用者来说都是一种很繁琐的…...

火山引擎声音复刻
首先,我需要确定火山引擎是什么,扣子声音复刻具体指什么。火山引擎是字节跳动旗下的云服务平台,提供各种技术解决方案。声音复刻应该属于他们的AI语音相关服务。 接下来,用户可能想知道这个功能的应用场景。比如,企业用…...

【数据分析】Pandas
目录 🌟 前言🏗️ 技术背景与价值🩹 当前技术痛点🛠️ 解决方案概述👥 目标读者说明 🧠 一、技术原理剖析📊 核心概念图解💡 核心作用讲解🔧 关键技术模块说明⚖️ 技术选…...

【ROS2】Qt Debug日志重定向到ROS2日志管理系统中
1、注册消息处理函数 Qt 利用 qInstallMessageHandler 接口可以 注册消息处理函数; 将QDebug等输出重定向到ROS2的日志管理中,使用 RCLCPP_DEBUG 输出日志 示例: 1)定义消息处理函数 namespace GW {void ros2Logger(QtMsgType type, const QMessageLogContext &cont…...

经典SQL查询问题的练习第一天
首先有三张表,学生表、课程表、成绩表 student:studentId,studentName; course:courseId,courseName,teacher; score:score,studentId,courseId; 接着有以下几道题目: ①查询课程编号为‘0006’的总成绩: 首先总成绩&#x…...

ubuntu 22.04安装k8s高可用集群
文章目录 1.环境准备(所有节点)1.1 关闭无用服务1.2 环境和网络1.3 apt源1.4 系统优化1.5 安装nfs客户端 2. 装containerd(所有节点)3. master的高可用方案(master上操作)3.1 安装以及配置haproxyÿ…...

使用java实现word转pdf,html以及rtf转word,pdf,html
word,rtf的转换有以下方案,想要免费最靠谱的是LibreOffice方案, LibreOffice 是一款 免费、开源、跨平台 的办公软件套件,旨在为用户提供高效、全面的办公工具,适用于个人、企业和教育机构。它支持多种操作系统(Windows、macOS、…...

使用LSTM进行时间序列分析
LSTM(长短期记忆网络,Long Short-Term Memory)是一种特殊的循环神经网络(RNN),专门用于处理时间序列数据。由于其独特的结构设计,LSTM能够有效地捕捉时间序列中的长期依赖关系,这使得…...

【密码学——基础理论与应用】李子臣编著 第十三章 数字签名 课后习题
题目 逐题解析 13.1 知道p83,q41,h2,g4,x57,y77。 我看到答案,“消息M56”的意思居然是杂凑值,也就是传统公式的H(M)。 选择k23,那么r(g^k mod p) mod q 51 mod 4110,sk(H(M)xr) mod q29 ws mod q17,u1(mw) mod q9,u2(rw) m…...

k8s中kubeSphere的安装使用+阿里云私有镜像仓库配置完整步骤
一、实验目的 1、掌握kubeSphere 的安装部署 2、掌握kubesphere 使用外部镜像仓库; 2、熟悉图像化部署任务:产生pod---定义服务--验证访问 本次实验旨在通过 KubeSphere 平台部署基于自定义镜像(nginx:1.26.0 )的有状态副本集…...

Agilent安捷伦Cary3500 UV vis光谱仪Cary60分光光度计Cary1003004000500060007000 UV visible
Agilent安捷伦Cary3500 UV vis光谱仪Cary60分光光度计Cary1003004000500060007000 UV visible...

JSON解析性能优化全攻略:协程调度器选择与线程池饥饿解决方案
简介 JSON解析是现代应用开发中的基础操作,但在使用协程处理时,若调度器选择不当,会导致性能严重下降。特别是当使用Dispatchers.IO处理JSON解析时,可能触发线程池饥饿,进而引发ANR或系统卡顿。本文将深入剖析这一问题的技术原理,提供全面的性能检测方法,并给出多种优化…...

arcgis js 4.x 的geometryEngine计算距离、面积、缓冲区等报错、失败
在arcgis js 4.x版本中geometryEngine.geodesicArea计算面积时,有时会失败,失败的主要原因是,当前底图的坐标系不是WGS84大地坐标系(代号4326)或者web墨卡托投影(代号102113, 102100, 3857这三种之一&#…...

vSphere 7.0 client 提示HTTP状态 500- 内部服务器错误
1 .检查服务状态 通过5480端口登录vCenter管理界面(https://<vCenter_IP>:5480),查看自动启动的服务是否正常运行,尝试手动重启异常服务14若管理界面无法访问,通过SSH连接后执行命令:service-control --start --all 2. …...

用 Python 打造你的专属虚拟试衣间!——AI+AR 如何改变时尚体验
友友们好! 我是Echo_Wish,我的的新专栏《Python进阶》以及《Python!实战!》正式启动啦!这是专为那些渴望提升Python技能的朋友们量身打造的专栏,无论你是已经有一定基础的开发者,还是希望深入挖掘Python潜力的爱好者,这里都将是你不可错过的宝藏。 在这个专栏中,你将会…...

Java与Flutter集成开发跨平台应用:从核心概念到生产实践
在2025年的移动开发领域,跨平台技术已成为主流,Flutter凭借其高性能、统一的UI和跨平台能力,成为开发iOS、Android、Web和桌面应用的首选框架。根据2024年Stack Overflow开发者调查,Flutter的使用率增长了35%,特别是在…...

SpringAI 大模型应用开发篇-纯 Prompt 开发(舔狗模拟器)、Function Calling(智能客服)、RAG (知识库 ChatPDF)
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 大模型应用开发技术框架 2.0 纯 Prompt 模式 2.1 核心策略 2.2 减少模型"幻觉"的技巧 2.3 提示词攻击防范 2.4 纯 Prompt 大模型开发(舔狗模拟器) 3.0 Function Calling 模式 3.1 …...

微信小程序的软件测试用例编写指南及示例--性能测试用例
以下是针对微信小程序的性能测试用例补充,结合代码逻辑和实际使用场景,从加载性能、渲染性能、资源占用、交互流畅度等维度设计测试点,并标注对应的优化方向: 一、加载性能测试用例 测试项测试工具/方法测试步骤预期结果优化方向冷启动加载耗时微信开发者工具「性能」面板…...

Unsupervised Learning-Word Embedding
传统的1 of N 的encoding无法让意义相近的词汇产生联系,word class可以将相近的词汇放到一起 但是word class不能表示class间的关系,所以引入了word embedding(词嵌入) 我们生成词向量是一种无监督的过程(没有label 自编码器是一种人工神经网络,主要用于无监督学习…...

远控安全进阶之战:TeamViewer/ToDesk/向日葵设备安全策略对比
【作者主页】Francek Chen 【文章摘要】在数字化时代,卓越的远程控制软件需兼顾功能与体验,包括流畅连接、高清画质、低门槛UI设计、毫秒级延迟及多功能性,同时要有独树一帜的远控安全技术,通过前瞻性安全策略阻挡网络风险&#x…...

变量的计算
不同类型变量之间的计算 数字型变量可以直接计算 在python中,数字型变量可以直接通过算术运算符计算bool型变量:True 对应数字1 ;False 对应数字0、 字符串变量 使用 拼接字符串 使用 * 拼接指定倍数的相同字符串 变量的输入:&…...

深入了解linux系统—— 库的制作和使用
什么是库? 库,简单来说就是现有的,成熟的代码; 就比如我们使用的C语言标准库,我们经常使用输入scanf和输出printf,都是库里面给我们实现好的,我们可以直接进行服用。 库呢又分为静态库和动态…...

Java中的设计模式:单例模式的深入探讨
单例模式的原理 单例模式的核心在于控制实例的数量。在Java中,类的实例化通常是由new关键字完成的。然而,单例模式通过将构造器私有化(private),阻止了外部通过new关键字直接创建类的实例。取而代之的是,单…...

View的工作流程——measure
1.DecorView被加载到Window当中 调用Activity的startActivity方法的时候,最终调用的是ActivityThread的handleLaunchActivity方法来创建Activity。 onResume方法也是在ActivityThread中的handleResumeActivity方法中被调用的,我们之前提到的DecorView就…...
)
【系统架构设计师】2025年上半年真题论文回忆版: 论软件测试方法及应用(包括解题思路和参考素材)
更多内容请见: 备考系统架构设计师-专栏介绍和目录 文章目录 真题题目(2025年上半年 试题4)解题思路1. 核心问题2. 论文目标3. 突出系统架构与 AI 的协同价值论文素材参考1、AI工具在生成测试用例过程中的具体应用2、AI测试用例生成的基本处理流程真题题目(2025年上半年 试…...

《软件工程》第 13 章 - 软件维护
知识思维导图 13.1 软件维护与进化的概念 1. 核心概念 软件维护:软件交付使用后,为纠正错误、改善性能或其他属性而进行的修改过程软件进化:随着时间推移,软件系统为适应环境变化和用户需求而不断演变的过程 2. 维护类型&#…...
