对数的运算困惑
难点总结
学生在对数运算中的难点分析:
一、不理解对数,不会用对数公式或错用对数公式
①对数 l o g 2 3 log_23 log23和指数幂 2 3 2^3 23一样,也就是个实数而已,所以其也会有加减乘除乘方开方等运算;
比如 2 2 + l o g 2 3 = 2 2 ⋅ 2 l o g 2 3 = 4 ⋅ 3 = 12 2^{2+log_23}=2^2\cdot 2^{log_23}=4\cdot 3=12 22+log23=22⋅2log23=4⋅3=12;
②准确记忆对数的运算公式和法则,
【相关复习】指数幂的运算1
a b = N a^b=N ab=N(指数式) ⟺ \Longleftrightarrow ⟺ b = l o g a N b=log_aN b=logaN(对数式);
对数的性质: l o g a 1 = 0 log_a1=0 loga1=0, l o g a a = 1 log_aa=1 logaa=1;
对数的运算法则:
l o g a M N = l o g a M + l o g a N log_aMN=log_aM+log_aN logaMN=logaM+logaN;注意字母的取值, a > 0 a>0 a>0且 a ≠ 1 a\neq1 a=1, M > 0 M>0 M>0且 N > 0 N>0 N>0,后者学生在做变换时容易忘记;
l o g a M N = l o g a M − l o g a N log_a\cfrac{M}{N}=log_aM-log_aN logaNM=logaM−logaN; l o g a M n = n l o g a M log_aM^n=nlog_aM logaMn=nlogaM;
对数恒等式: a l o g a N = N a^{log_aN}=N alogaN=N;
对数换底公式: l o g a b = l o g c b l o g c a ( a > 0 , a ≠ 1 ; c > 0 , c ≠ 1 ; b > 0 ) log_ab=\cfrac{log_cb}{log_ca}(a>0,a\neq 1;c>0,c\neq 1;b>0) logab=logcalogcb(a>0,a=1;c>0,c=1;b>0)
常用公式1: l o g a b ⋅ l o g b c ⋅ l o g c d = l o g a d log_ab\cdot log_bc\cdot log_cd= log_ad logab⋅logbc⋅logcd=logad; l o g a b ⋅ l o g b c ⋅ l o g c a = l o g a a = 1 log_ab\cdot log_bc\cdot log_ca= log_aa=1 logab⋅logbc⋅logca=logaa=1;
l o g a b ⋅ l o g b a = 1 log_ab\cdot log_ba=1 logab⋅logba=1; l n e = 1 lne=1 lne=1; l g 2 + l g 5 = l g 10 = 1 lg2+lg5=lg10=1 lg2+lg5=lg10=1;
常用公式2: l o g a m b n = n m l o g a b ( m , n ∈ R , a > 0 , a ≠ 1 , b > 0 ) log_{a^m}{b^n}=\cfrac{n}{m}log_ab(m,n\in R,a>0,a\neq 1,b>0) logambn=mnlogab(m,n∈R,a>0,a=1,b>0)
③正用、逆用、变用公式;
l o g a M + l o g a N = l o g a M N log_aM+log_aN=log_aMN logaM+logaN=logaMN; l o g a M − l o g a N = l o g a M N log_aM-log_aN=log_a\cfrac{M}{N} logaM−logaN=logaNM;
n l o g a M = l o g a M n nlog_aM=log_aM^n nlogaM=logaMn; n m l o g a b = l o g a m b n \cfrac{n}{m}log_ab=log_{a^m}{b^n} mnlogab=logambn
④错用公式: l o g a ( M + N ) = l o g a M + l o g a N log_a(M+N)=log_aM+log_aN loga(M+N)=logaM+logaN; l o g a ( M ⋅ N ) = l o g a M ⋅ l o g a N log_a(M\cdot N)=log_aM\cdot log_aN loga(M⋅N)=logaM⋅logaN;
二、知道对数的公式和运算法则,但不会灵活运用,对公式中的字母的内涵不理解;
化简 ( l o g 2 4 ) l o g 2 3 = 3 (log_24)^{log_23}=3 (log24)log23=3; l o g 2 l o g 2 16 = l o g 2 4 = 2 log_2^{\;\;log_216}=log_24=2 log2log216=log24=2;
化简 l o g 2 25 ⋅ l o g 3 4 ⋅ l o g 5 9 = 8 log_225\cdot log_34\cdot log_59=8 log225⋅log34⋅log59=8;提示:换底公式
化简 l g 3
相关文章:

对数的运算困惑
难点总结 学生在对数运算中的难点分析: 一、不理解对数,不会用对数公式或错用对数公式 ①对数 l o g 2 3 log_23 log23和指数幂 2 3 2^3 23一样,也就是个实数而已,所以其也会有加减乘除乘方开方等运算; 比如 2 2 + l o g 2 3 = 2 2 ⋅ 2 l o g 2 3 = 4 ⋅ 3 = 12 2^{2…...
)
C++ 图像处理库 CxImage 简介 (迁移至OpenCV)
文章目录 核心功能特点局限性与替代方案常用方法构造函数从数组创建图像访问属性访问像素点Windows平台支持 常用方法迁移至OpenCV CxImage 是一款功能强大的图像处理类库,主要用于 Windows 平台的图像处理任务。它支持多种图像格式的加载、保存、编辑及特效处理&am…...

linux系统与shell 笔记
Linux 系统 Linux 是一种开源的操作系统内核,基于 Unix 设计,具有多用户、多任务、高稳定性和安全性的特点。它广泛应用于服务器、嵌入式设备和个人计算机领域。Linux 系统的核心组件包括内核、系统库、工具链和用户界面(如命令行或图形界面…...

尚硅谷redis7 86 redis集群分片之3主3从集群搭建
86 redis集群分片之3主集群搭建 3主3从redis集群配置 找3台真实虚拟机,各自新建 mķdir -p /myredis/cluster 新建6个独立的redis实例服务 IP:192.168.111.175端口6381/端口6382 vim /myredis/cluster/redisCluster6381.conf bind 0.0.0.0 daemonize yes protected-mode no …...
)
Kaggle-Predict Calorie Expenditure-(回归+xgb+cat+lgb+模型融合+预测结果)
Predict Calorie Expenditure 题意: 给出每个人的基本信息,预测运动后的卡路里消耗值。 数据处理: 1.构造出人体机能、运动相关的特征值。 2.所有特征值进行从新组合,注意唯独爆炸 3.对连续信息分箱变成离散 建立模型&#x…...

【解决办法】Git报错error: src refspec main does not match any.
在命令行中使用 Git 进行 git push -u origin main 操作时遇到报错error: src refspec main does not match any。另一个错误信息是:error: failed to push some refs to https://github.com/xxx/xxx.git.这是在一个新设备操作时遇到的问题,之前没有注意…...

React与Vue的内置指令对比
React 与 Vue 在内置指令的设计理念和实现方式上有显著差异。Vue 提供了一套丰富的模板指令系统,而 React 更倾向于通过原生 JavaScript 语法和 JSX 实现类似功能。以下是两者的核心对比: 一、条件渲染 Vue 使用 “v-if”/ “v-else” 指令,…...

2025年5月24号高项综合知识真题以及答案解析(第1批次)
2025年5月24号高项综合知识真题以及答案解析...

【NATURE氮化镓】GaN超晶格多沟道场效应晶体管的“闩锁效应”
2025年X月X日,布里斯托大学的Akhil S. Kumar等人在《Nature Electronics》期刊发表了题为《Gallium nitride multichannel devices with latch-induced sub-60-mV-per-decade subthreshold slopes for radiofrequency applications》的文章,基于AlGaN/GaN超晶格多通道场效应晶…...

Ubuntu24.04换源方法(新版源更换方式,包含Arm64)
一、源文件位置 Ubuntu24.04的源地址配置文件发生改变,不再使用以前的sources.list文件,升级24.04之后,而是使用如下文件 /etc/apt/sources.list.d/ubuntu.sources二、开始换源 1. 备份源配置文件 sudo cp /etc/apt/sources.list.d/ubunt…...

26 C 语言函数深度解析:定义与调用、返回值要点、参数机制(值传递)、原型声明、文档注释
1 函数基础概念 1.1 引入函数的必要性 在《街霸》这类游戏中,实现出拳、出脚、跳跃等动作,每项通常需编写 50 - 80 行代码。若每次调用都重复编写这些代码,程序会变得臃肿不堪,代码可读性与维护性也会大打折扣。 为解决这一问题&…...

彻底理解一个知识点的具体步骤
文章目录 前言一、了解概念(是什么)二、理解原理(为什么)三、掌握方法(怎么用) 四、动手实践(会用)五、类比拓展(迁移能力)六、总结归纳(融会贯通…...

FFmpeg 时间戳回绕处理:保障流媒体时间连续性的核心机制
FFmpeg 时间戳回绕处理:保障流媒体时间连续性的核心机制 一、回绕处理函数 /** * Wrap a given time stamp, if there is an indication for an overflow * * param st stream // 传入一个指向AVStream结构体的指针,代表流信息 * pa…...

yolov8改进模型
YOLOv8 作为当前 YOLO 系列的最新版本,已经具备出色的性能。若要进一步改进,可以从网络架构优化、训练策略增强、多任务扩展和部署效率提升四个方向入手。以下是具体改进思路和实现示例: 1. 网络架构优化 (1) 骨干网络增强 引入 Transform…...

PostgreSQL日常运维
目录 一、PostgreSQL基础操作 1.1 登录数据库 1.2 数据库管理 1.3 数据表操作 二、数据备份与恢复 2.1 备份工具pg_dump 2.2 恢复工具pg_restore与psql 2.3 备份策略建议 三、模式(Schema) 3.1 模式的核心作用 3.2 模式操作全流程 四、远程连…...
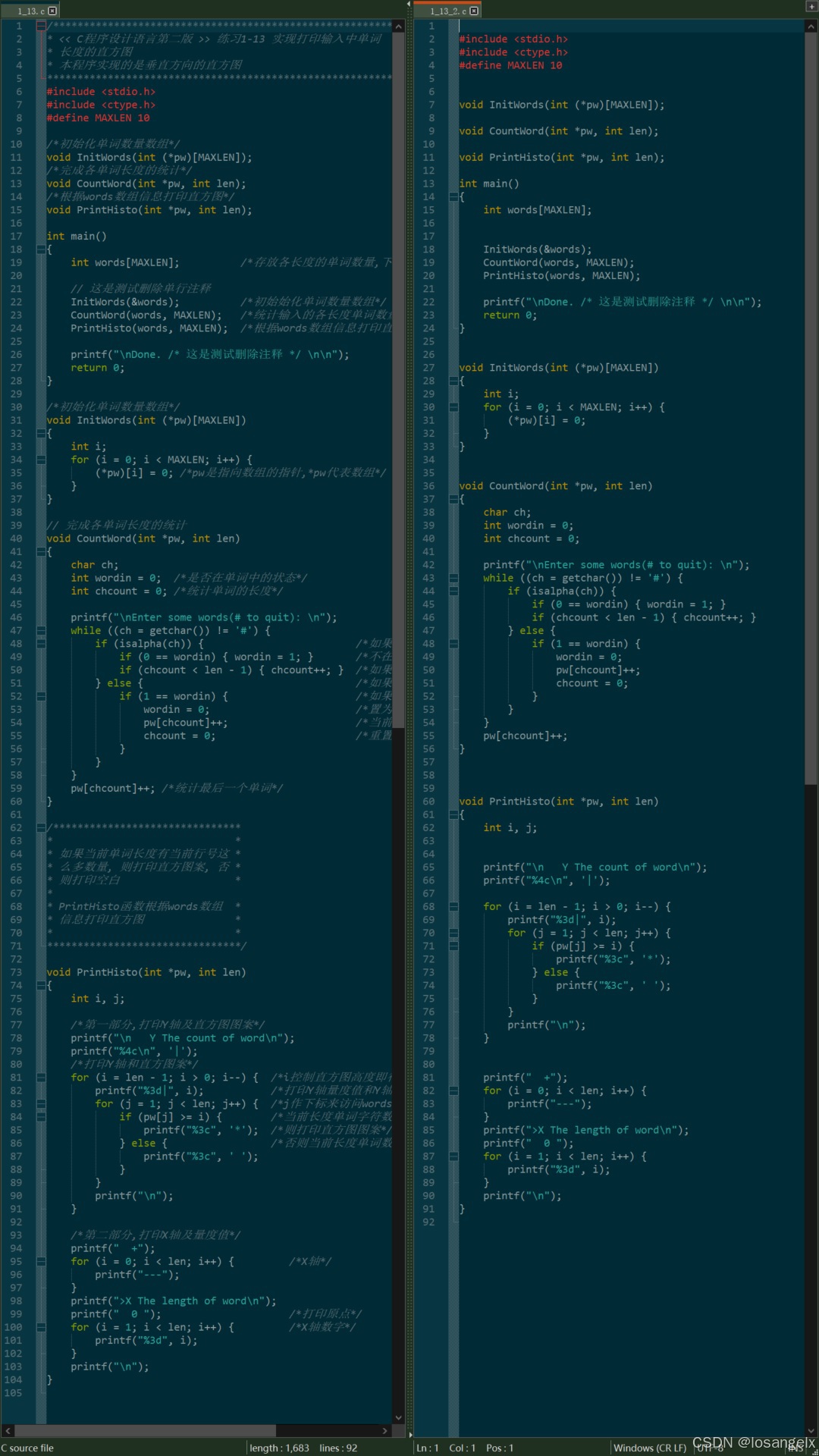
<< C程序设计语言第2版 >> 练习 1-23 删除C语言程序中所有的注释语句
1. 前言 本篇文章介绍的是实现删除C语言源文件中所有注释的功能.希望可以给C语言初学者一点参考.代码测试并不充分, 所以肯定还有bug, 有兴趣的同学可以改进. 原题目是: 练习1-23 编写一个删除C语言程序中所有的注释语句. 要正确处理带引号的字符串与字符常量. 在C语言中, 注释…...

Fluence (FLT) 2026愿景:RWA代币化加速布局AI算力市场
2025年5月29日,苏黎世 - Fluence,企业级去中心化计算平台,荣幸地揭开其2026愿景的面纱,并宣布将于6月1日起启动四大新举措。 Fluence 成功建立、推出并商业化了其去中心化物理基础设施计算网络(DePIN)&…...

如何撰写一篇优质 Python 相关的技术文档 进阶指南
💝💝💝在 Python 项目开发与协作过程中,技术文档如同与团队沟通的桥梁,能极大提高工作效率。但想要打造一份真正实用且高质量的 Python 技术文档类教程,并非易事,需要在各个环节深入思考与精心打…...

选择if day5
5.scanf(“空白符”) 空白符作用表示匹配任意多个空白符 进入了内存缓冲区(本质就是一块内存空间) 6.scanf读取问题: a.遇到非法字符读取结束 2. %*d * 可以跳过一个字符 eg:%d%*d%d 读取第一和第三个字符…...

MiniMax V-Triune让强化学习(RL)既擅长推理也精通视觉感知
MiniMax 近日在github上分享了技术研究成果——V-Triune,这次MiniMax V-Triune的发布既是AI视觉技术也是应用工程上的一次“突围”,让强化学习(RL)既擅长推理也精通视觉感知,其实缓解了传统视觉RL“鱼和熊掌不可兼得”…...

Hash 的工程优势: port range 匹配
昨天和朋友聊到 “如何匹配一个 port range”,觉得挺有意思,简单写篇散文。 回想起十多年前,我移植并优化了 nf-HiPAC,当时还看不上 ipset hash,后来大约七八年前,我又舔 nftables,因为用它可直…...

同为.net/C#的跨平台运行时的mono和.net Core有什么区别?
Mono 和 .NET Core(现已统一为 .NET)都是 .NET 生态的跨平台实现,但它们在设计目标、技术特性和应用场景上有显著区别。以下是详细对比: 1. 历史背景 项目诞生时间开发者当前状态Mo…...

前端安全直传MinIO方案
目的:前端直接上传文件到Minio,不通过服务器中转文件。密钥不能在前端明文传输。 ## 一、架构设计 mermaid sequenceDiagram 前端->>后端: 1.请求上传凭证 后端->>MinIO: 2.生成预签名URL 后端-->>前端: 3.返回预签名URL 前端->…...

HackMyVM-Dejavu
信息搜集 主机发现 ┌──(root㉿kali)-[~] └─# arp-scan -l Interface: eth0, type: EN10MB, MAC: 00:0c:29:39:60:4c, IPv4: 192.168.43.126 Starting arp-scan 1.10.0 with 256 hosts (https://github.com/royhills/arp-scan) 192.168.43.1 c6:45:66:05:91:88 …...
)
LeetCode Hot100(动态规划)
70. 爬楼梯 题目: 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 题解: 不难发现,每一次都是从i-1或者i-2爬上来的,我们加起来求和即可 class So…...

Opencv实用操作5 图像腐蚀膨胀
相关函数 腐蚀函数 img1_erosion cv2.erode(img1,kernel,iterations1) (图片,卷积核,次数) 膨胀函数 img_dilate cv2.dilate(img2,kernel1,iterations1) (图片,卷积核,次数)…...

【赵渝强老师】OceanBase的部署架构
OceanBase数据库支持无共享(Shared-Nothing,SN)模式和共享存储(Shared-Storage,SS)模式两种部署架构。 一、 无共享(Shared-Nothing,SN)模式 在SN模式下,各…...
混合云架构部署)
(18)混合云架构部署
文章目录 🚀 混合云架构部署:Java应用的云原生之旅🌩️ 混合云架构简介⚡ Java应用云原生部署五大核心技术1️⃣ 容器化与编排技术2️⃣ 服务网格与API网关3️⃣ CI/CD自动化流水线4️⃣ 多云管理平台5️⃣ 云原生Java框架与运行时 …...

c/c++的opencv霍夫变换
OpenCV中的霍夫变换 (C/C) Hough Transform 霍夫变换 (Hough Transform) 是一种在图像分析中用于检测几何形状(如直线、圆形等)的特征提取技术。它通过一种投票机制在参数空间中寻找特定形状的实例。OpenCV 库为 C 开发者提供了强大且易用的霍夫变换函数…...
 --- AudioRecord录音逻辑分析(一))
AAOS系列之(七) --- AudioRecord录音逻辑分析(一)
一文讲透AAOS架构,点到为止不藏私 📌 这篇帖子给大家分析下 AudioRecord的初始化 1. 场景介绍: 在 AAOS 的 Framework 开发中,录音模块几乎是每个项目都会涉及的重要组成部分。无论是语音控制、车内对讲(同行者模式)…...
