代码随想录算法训练营 Day60 图论Ⅹ Bellmen_ford 系列算法
图论
题目
94. 城市间货物运输 I
Bellmen_ford 队列优化算法 SPFA
大家可以发现 Bellman_ford 算法每次松弛 都是对所有边进行松弛。
但真正有效的松弛,是基于已经计算过的节点在做的松弛。 
本图中,对所有边进行松弛,真正有效的松弛,只有松弛边(节点1->节点2) 和边(节点1->节点3) 因此只要记录上一次松驰过的边即可
模拟过程
我们依然使用minDist数组来表达起点到各个节点的最短距离,例如minDist[3] = 5 表示起点到达节点3 的最小距离为5初始化,起点为节点1,起点到起点的最短距离为0,所以minDist[1] 为 0。将节点1 加入队列 (下次松弛从节点1开始)

从队列里取出节点1,松弛节点1 作为出发点连接的边(节点1 -> 节点2)和边(节点1 -> 节点3)
边:节点1 -> 节点2,权值为1 ,minDist[2] > minDist[1] + 1 ,更新 minDist[2] = minDist[1] + 1 = 0 + 1 = 1 。边:节点1 -> 节点3,权值为5 ,minDist[3] > minDist[1] + 5,更新 minDist[3] = minDist[1] + 5 = 0 + 5 = 5。将节点2、节点3 加入队列

从队列里取出节点2,松弛节点2 作为出发点连接的边(节点2 -> 节点4)和边(节点2 -> 节点5)
边:节点2 -> 节点4,权值为1 ,minDist[4] > minDist[2] + (-3) ,更新 minDist[4] = minDist[2] + (-3) = 1 + (-3) = -2 。边:节点2 -> 节点5,权值为2 ,minDist[5] > minDist[2] + 2 ,更新 minDist[5] = minDist[2] + 2 = 1 + 2 = 3 。将节点4,节点5 加入队列

从队列里出去节点3,松弛节点3 作为出发点连接的边。
因为没有从节点3作为出发点的边,所以这里就从队列里取出节点3就好,不用做其他操作,如图:

从队列中取出节点4,松弛节点4作为出发点连接的边(节点4 -> 节点6)边:节点4 -> 节点6,权值为4 ,minDist[6] > minDist[4] + 4,更新 minDist[6] = minDist[4] + 4 = -2 + 4 = 2。将节点6加入队列

从队列中取出节点5,松弛节点5作为出发点连接的边(节点5 -> 节点3),边(节点5 -> 节点6)
边:节点5 -> 节点3,权值为1 ,minDist[3] > minDist[5] + 1 ,更新 minDist[3] = minDist[5] + 1 = 3 + 1 = 4。边:节点5 -> 节点6,权值为-2 ,minDist[6] > minDist[5] + (-2) ,更新 minDist[6] = minDist[5] + (-2) = 3 - 2 = 1。如图,将节点3加入队列,因为节点6已经在队列里所以不用重复添加

所以我们在加入队列的过程可以有一个优化,用visited数组记录已经在队列里的元素,已经在队列的元素不用重复加入,从队列中取出节点6,松弛节点6 作为出发点连接的边。节点6作为终点,没有可以出发的边。同理从队列中取出节点3,也没有可以出发的边,所以直接从队列中取出。

这样我们就完成了基于队列优化的bellman_ford的算法模拟过程。大家可以发现基于队列优化的算法,要比bellman_ford 算法减少很多无用的松弛情况,特别是对于边数众多的大图优化效果明显。
代码实现类似于 dijkstra 的优化版本,需要将图以邻接表的形式构建
#include <iostream>
#include <vector>
#include <list>
#include <queue>
#include <climits>using namespace std;struct Edge {int to;int val;Edge(int t, int w): to(t), val(w) {}
};int main() {int n, m, x, y, val;cin >> n >> m;vector<list<Edge>> grid(n+1);vector<bool> isInQueue(n+1);// 构造邻接表for (int i = 0; i < m; ++i) {cin >> x >> y >> val;grid[x].push_back({Edge(y, val)});}int start = 1;int end = n;vector<int> minDist(n+1, INT_MAX);minDist[start] = 0;queue<int> que;que.push(start);// 使用队列while (!que.empty()) {int cur = que.front();// 从队列里取出的时候,要取消标记,我们只保证已经在队列里的元素不用重复加入isInQueue[cur] = false;que.pop();for (Edge e : grid[cur]) {int from = cur;int to = e.to;int price = e.val;if (minDist[to] > minDist[from] + price) {minDist[to] = minDist[from] + price;// 不再添加to这个下标元素 相当于已经访问过if (isInQueue[to] == false) {que.push(to);isInQueue[to] = true;}}}}if(minDist[end] == INT_MAX) cout << "unconnected" << endl;else cout << minDist[end] << endl;return 0;
}
95. 城市间货物运输 II
涉及到负权回路的情况(存在环路,权值为负,会导致无限循环值越来越小)
非负权回路,松弛 n-1 次以上不会有变换,但是设计负权回路就会越来越小

那么解决本题的核心思路,就是在 kama94.城市间货物运输I 的基础上,再多松弛一次,看minDist数组是否发生变化。 如果再松弛一次结果变换则存在负权回路
// Bellman_ford 算法实现
#include <iostream>
#include <vector>
#include <climits>using namespace std;int main() {int n, m, x, y, val;cin >> n >> m;vector<vector<int>> grid;vector<int> minDist(n+1, INT_MAX);for (int i = 0; i < m; ++i) {cin >> x >> y >> val;grid.push_back({x, y, val});}int start = 1;int end = n;bool isCircle = false;minDist[start] = 0;// 多做一次负权回路for (int i = 1; i <= n; ++i) {for (vector<int>& edge : grid) {int from = edge[0];int to = edge[1];int price = edge[2];if (i < n) {if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) {minDist[to] = minDist[from] + price;}}else {if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) isCircle = true;}}}if (isCircle) cout << "circle" << endl;else if (minDist[end] == INT_MAX) cout << "unconnected" << endl;else cout << minDist[end] << endl;return 0;
}// Bellman_ford 队列优化版本 SPFA 实现
#include <iostream>
#include <vector>
#include <queue>
#include <list>
#include <climits>
using namespace std;struct Edge { //邻接表int to; // 链接的节点int val; // 边的权重Edge(int t, int w): to(t), val(w) {} // 构造函数
};int main() {int n, m, p1, p2, val;cin >> n >> m;vector<list<Edge>> grid(n + 1); // 邻接表// 将所有边保存起来for(int i = 0; i < m; i++){cin >> p1 >> p2 >> val;// p1 指向 p2,权值为 valgrid[p1].push_back(Edge(p2, val));}int start = 1; // 起点int end = n; // 终点vector<int> minDist(n + 1 , INT_MAX);minDist[start] = 0;queue<int> que;que.push(start); // 队列里放入起点 vector<int> count(n+1, 0); // 记录节点加入队列几次count[start]++;vector<bool> isInQueue(n+1, false);isInQueue[start] = true;bool flag = false;while (!que.empty()) {int node = que.front(); que.pop();isInQueue[node] = false;for (Edge edge : grid[node]) {int from = node;int to = edge.to;int value = edge.val;if (minDist[to] > minDist[from] + value) { // 开始松弛minDist[to] = minDist[from] + value;if (!isInQueue[to]) {que.push(to);isInQueue[to] = true;count[to]++; if (count[to] == n) {// 如果加入队列次数超过 n-1次 就说明该图与负权回路flag = true;while (!que.empty()) que.pop();break;}}}}}if (flag) cout << "circle" << endl;else if (minDist[end] == INT_MAX) {cout << "unconnected" << endl;} else {cout << minDist[end] << endl;}}
96. 城市间货物运输 III
给出尽可能路过最多城市的最短路径
本题是最多经过 k 个城市, 那么是 k + 1条边相连的节点。 这里可能有录友想不懂为什么是k + 1,来看这个图
节点1 最多已经经过2个节点 到达节点4,那么中间是有多少条边呢,是 3 条边对吧。
所以本题就是求:起点最多经过k + 1 条边到达终点的最短距离。
对所有边松弛一次,相当于计算起点到达与起点一条边相连的节点的最短距离,那么对所有边松弛 k + 1次,就是求起点到达与起点k + 1条边相连的节点的最短距离。 理解以上内容,其实本题代码就很容易了,bellman_ford 标准写法是松弛 n-1 次,本题就松弛 k + 1次就好。
但是松弛 k + 1次代码有错,具体分析如下
起点为节点1,起点到起点的距离为0,所以 minDist[1] 初始化为0 ,如图

其他节点对应的minDist初始化为max,因为我们要求最小距离,那么还没有计算过的节点默认是一个最大数,这样才能更新最小距离。当我们开始对所有边开始第一次松弛:边:节点1 -> 节点2,权值为-1 ,minDist[2] > minDist[1] + (-1),更新 minDist[2] = minDist[1] + (-1) = 0 - 1 = -1

边:节点2 -> 节点3,权值为1 ,minDist[3] > minDist[2] + 1 ,更新 minDist[3] = minDist[2] + 1 = -1 + 1 = 0 ,如图

边:节点3 -> 节点1,权值为-1 ,minDist[1] > minDist[3] + (-1),更新 minDist[1] = 0 + (-1) = -1 ,如图:

边:节点3 -> 节点4,权值为1 ,minDist[4] > minDist[3] + 1,更新 minDist[4] = 0 + 1 = 1 ,如图:

理论上来说,对所有边松弛一次,相当于计算 起点到达 与起点一条边相连的节点 的最短距离。
而且对所有边的后面几次松弛,同样是更新了所有的节点,说明至多经过k 个节点这个限制根本没有限制住,每个节点的数值都被更新了。
这是为什么?
在上面画图距离中,对所有边进行第一次松弛,在计算边(节点2 -> 节点3) 的时候,更新了节点3。

理论上来说节点3 应该在对所有边第二次松弛的时候才更新。 这因为当时是基于已经计算好的 节点2(minDist[2])来做计算了。minDist[2]在计算边:(节点1 -> 节点2)的时候刚刚被赋值为 -1。
这样就造成了一个情况,即:计算minDist数组的时候,基于了本次松弛的 minDist数值,而不是上一次松弛时候minDist的数值。所以在每次计算 minDist 时候,要基于 对所有边上一次松弛的 minDist 数值才行,所以我们要记录上一次松弛的minDist。
具体代码添加了 minDist 的 copy
// 朴素 Bellman_ford方法
#include <iostream>
#include <vector>
#include <climits>using namespace std;int main() {int n, m, x, y, val, src, dst, k;cin >> n >> m;vector<vector<int>> grid;vector<int> minDist(n+1, INT_MAX);vector<int> minDistCopy(n+1);for (int i = 0; i < m; ++i) { cin >> x >> y >> val;grid.push_back({x, y, val});}cin >> src >> dst >> k;minDist[src] = 0;// 最多经过k个城市,最多走过k+1条边for (int i = 1; i <= k + 1; ++i) {// 获取上一次计算结果minDistCopy = minDist;for (vector<int>& side : grid) {int from = side[0];int to = side[1];int price = side[2];// 使用上一次copy计算if (minDistCopy[from] != INT_MAX && minDist[to] > minDistCopy[from] + price) {minDist[to] = minDistCopy[from] + price;}}}if (minDist[dst] == INT_MAX) cout << "unreachable" << endl;else cout << minDist[dst] << endl;
}// bellman_ford 队列优化 SPFA
#include <iostream>
#include <vector>
#include <queue>
#include <list>
#include <climits>using namespace std;struct Edge {int to;int val;Edge(int t, int w) : to(t), val(w) {}
};int main() {int n, m, x, y, val, src, dst, k;cin >> n >> m;vector<list<Edge>> grid(n+1);vector<int> minDist(n+1, INT_MAX);vector<int> minDistCopy(n+1);for (int i = 0; i < m; ++i) {cin >> x >> y >> val;grid[x].push_back(Edge(y, val));}cin >> src >> dst >> k;k++; // k+1minDist[src] = 0;queue<int> que;que.push(src);// k控制松弛次数int qSize = 0;while (k-- && !que.empty()) {// 开启新的队列vector<bool> isInQueue(n+1, false);minDistCopy = minDist;qSize = que.size();// 后--保证执行完全while (qSize--) {int cur = que.front();que.pop();isInQueue[cur] = false;for (Edge e : grid[cur]) {int from = cur;int to = e.to;int price = e.val;if (minDist[to] > minDistCopy[from] + price) {minDist[to] = minDistCopy[from] + price;if (!isInQueue[to]) {que.push(to);isInQueue[to] = true;}}}}}if (minDist[dst] == INT_MAX) cout << "unreachable" << endl;else cout << minDist[dst] << endl;
}
边的顺序会影响每一次扩展的结果,给出边的顺序为
我上面讲解中,给出的示例是这样的:
4 4
1 2 -1
2 3 1
3 1 -1
3 4 1
1 4 3
我将示例中边的顺序改一下,给成:
4 4
3 1 -1
3 4 1
2 3 1
1 2 -1
1 4 3
相同的图就会有不同的结果


推理一遍,初始化

边:节点3 -> 节点1,权值为-1 ,节点3还没有被计算过,节点1 不更新。
边:节点3 -> 节点4,权值为1 ,节点3还没有被计算过,节点4 不更新。
边:节点2 -> 节点3,权值为 1 ,节点2还没有被计算过,节点3 不更新。
边:节点1 -> 节点2,权值为 -1 ,minDist[2] > minDist[1] + (-1),更新 minDist[2] = 0 + (-1) = -1

可以发现 同样的图,边的顺序不一样,使用版本一的代码 每次松弛更新的节点也是不一样的。
而边的顺序是随机的,是题目给我们的,所以本题我们才需要 记录上一次松弛的minDist,来保障 每一次对所有边松弛的结果。
为什么必须使用 copy?
94.城市间货物运输I,是没有负权回路的,那么多松弛多少次,对结果都没有影响。求节点1 到 节点n 的最短路径,松弛n-1 次就够了,松弛 大于 n-1次,结果也不会变。 那么在对所有边进行第一次松弛的时候,如果基于本次计算的 minDist 来计算 minDist (相当于多做松弛了),也是对最终结果没影响。
95.城市间货物运输II 是判断是否有负权回路,一旦有负权回路,对所有边松弛 n-1 次以后,在做松弛 minDist 数值一定会变,根据这一点来判断是否有负权回路。所以,95.城市间货物运输II 只需要判断minDist数值变化了就行,而 minDist 的数值对不对,并不是我们关心的。
其关键在于本题的两个因素:
本题可以有负权回路,说明只要多做松弛,结果是会变的。
本题要求最多经过 k 个节点,对松弛次数是有限制的。
可以使用 dijkstra 吗?不可以因为 dijkstra 贪心策略导致找不到
参考:代码随想录
相关文章:

代码随想录算法训练营 Day60 图论Ⅹ Bellmen_ford 系列算法
图论 题目 94. 城市间货物运输 I Bellmen_ford 队列优化算法 SPFA 大家可以发现 Bellman_ford 算法每次松弛 都是对所有边进行松弛。 但真正有效的松弛,是基于已经计算过的节点在做的松弛。 本图中,对所有边进行松弛,真正有效的松弛&#…...

独立机构软件第三方检测:流程、需求分析及电商软件检验要点?
独立机构承担着对软件进行第三方检测的任务,这一环节对于提升软件的质量和稳定性起到了极其关键的作用。检测过程拥有一套完善的流程,目的在于确保检测结果的精确性,并保障软件达到高标准。 需求分析 确保软件测试需求清晰十分关键。我们需…...

Java构建Tree并实现节点名称模糊查询
乐于学习分享… 大家加油努力 package com.tom.backtrack;import lombok.Data; import lombok.Getter;import java.util.ArrayList; import java.util.List; import java.util.Objects;/*** 树节点** author zx* date 2025-05-27 19:51*/ Data public class TreeNode {private …...

shadcn/ui
文章目录 前言✅ 核心特点📦 支持组件(常用)🚀 安装使用(框架支持)初始化(Next.js 项目为例)添加一个组件 🧠 对比其他组件库📘 官方资源✅ 总结✅ 功能特性&…...

华为FreeArc能和其他华为产品共用充电线吗?
最近刚买的FreeArc终于到手啦,看到网上有朋友说,这次的耳机是不附带充电线,开箱后发现果真如此,那FreeArc到底用什么规格的充电线,能不能和华为的Type-C数据线通用,我来给大家解答一下吧! Free…...

[网页五子棋][匹配模式]创建房间类、房间管理器、验证匹配功能,匹配模式小结
文章目录 创建房间类创建房间类实现房间管理器 实现匹配器(3)验证匹配功能问题:匹配按钮不改变验证多开 小结 创建房间类 LOL,通过匹配的方式,自动给你加入到一个房间,也可手动创建游戏房间 这一局游戏,进行的“场所…...

实验设计与分析(第6版,Montgomery)第3章单因子实验:方差分析3.11思考题3.7 R语言解题
本文是实验设计与分析(第6版,Montgomery著,傅珏生译) 第3章单因子实验:方差分析3.11思考题3.7 R语言解题。主要涉及单因子方差分析,正态性假设检验,残差与拟合值的关系图,平方根变换。 X<-c(…...

【知识点】第2章:Python程序实例解析
文章目录 知识点整理Python程序语法元素分析 练习题判断题填空题选择题 知识点整理 Python程序语法元素分析 Python程序包括格式框架、注释、变量、表达式、分支语句、循环语句、函数等语法元素。 程序的格式框架 Python语言采用严格的 “缩进” 来表明程序的格式框架。缩进…...

从解决一个分享图片生成的历史bug出发,详解LayoutInflater和View.post的工作原理
问题背景 最近在项目中遇到一个问题:在档口分享功能中,需要动态生成一个分享图片。代码是这样写的: // 项目中的代码 val shareView LayoutInflater.from(thisStallMainActivityV1).inflate(R.layout.share_header_stall_main_layout, nul…...

Ubuntu 22.04 上使用 Docker 安装 RagFlow
GitHub地址:添加链接描述 RAGFlow 是一款开源的检索增强生成(Retrieval-Augmented Generation,简称 RAG)引擎,旨在通过深度文档理解技术,结合大语言模型(LLM),为用户提供高质量、可溯源的问答服务。 🚀 快速入门 RAGFlow 提供了便捷的部署方式,支持 Docker 环境。…...

每日Prompt:指尖做画
提示词 微缩景观,微距摄影,俯瞰角度,特写,硕大食指手指甲,一个小小的人正在做画,小人右手拿画笔,小人左手拿调色盘,在指甲上作画,画的是中国古代山水画,背景…...

Python打卡训练营day40——2025.05.30
知识点回顾: 彩色和灰度图片测试和训练的规范写法:封装在函数中 展平操作:除第一个维度batchsize外全部展平 dropout操作:训练阶段随机丢弃神经元,测试阶段eval模式关闭dropout 作业:仔细学习下测试和训练…...

Java八股-数据类型转换有哪些?类型互转会有什么问题?为什么用bigDecimal 不用double ?自动装箱和拆箱?包装类?
Java中有哪些数据类型转换? 显示类型转换:在前面一个括号,里面写上要转换的类型 隐式类型转换:小范围的数据类型转大范围的,int到long,float到double 字符串转整形或浮点:整形:In…...

redis未授权(CVE-2022-0543)
概述 Redis 默认绑定在 0.0.0.0:6379,在未配置防火墙或访问控制的情况下会将服务暴露在公网上。若未设置访问密码(默认通常为空),攻击者可直接未授权访问 Redis。利用 Redis 提供的 CONFIG 命令,攻击者可修改配置并将…...

【运维实战】Linux 中su和sudo之间的区别以及如何配置sudo!
Linux 系统相比其他操作系统具有更高的安全性,其安全机制的核心之一在于用户管理策略和权限控制--普通用户默认无权执行任何系统级操作。 若普通用户需要进行系统级变更,必须通过su或sudo命令提权。 1.su与sudo的本质区别 su 要求直接共享 root 密码&…...

LevelDB、BoltDB 和 RocksDB区块链应用比较
LevelDB、BoltDB 和 RocksDB 是三种常用的键值存储数据库,它们在区块链领域(如以太坊、比特币等)或其他高性能应用中有广泛应用。虽然它们都是嵌入式键值存储,但设计目标、性能特性、功能支持和适用场景有显著差异。以下是它们的详…...

c/c++的opencv图像金字塔缩放
图像金字塔缩放:OpenCV C/C 实践 📐 图像金字塔是计算机视觉中一种重要且基础的多尺度表示方法。它通过对原始图像进行连续的下采样(缩小)或上采样(放大)操作,生成一系列不同分辨率的图像。这些…...

PDF文件转换之输出指定页到新的 PDF 文件
背景 一份 PDF 学习资料需要打印其中某几页,文件有几百兆,看到 WPS 有PDF拆分功能,但是需要会员,开了一个月会员后完成了转换。突然想到,会员到期后如果还要拆解的话,怎么办呢?PDF 文件拆解功能…...

浏览器之禁止打开控制台【F12】
前言 在有时我们的日常开发工作中,有些项目要求我们增加禁用控制台的要求,这种虽然很鸡肋,但是它确实存在,并且会让哈哈心里觉得很有成就感。 所以今天他来了。 文章目录 前言无限debugger实现思路:效果如下࿱…...
(帮你生成 模块划分+页面+表设计、状态机、工作流、ER模型))
进阶智能体实战九、图文需求分析助手(ChatGpt多模态版)(帮你生成 模块划分+页面+表设计、状态机、工作流、ER模型)
🧠 基于 ChatGPT 多模态大模型的需求文档分析助手 本文将介绍如何利用 OpenAI 的 GPT-4o 多模态能力,构建一个智能的需求文档分析助手,自动提取功能模块、菜单设计、字段设计、状态机、流程图和 ER 模型等关键内容。 一、🔧 环境准备 在开始之前,请确保您已经完成了基础…...

GEARS以及与基础模型结合
理解基因扰动的反应是众多生物医学应用的核心。然而,可能的多基因扰动组合数量呈指数级增长,严重限制了实验探究的范围。在此,图增强基因激活与抑制模拟器(GEARS),将深度学习与基因-基因关系知识图谱相结合…...
机制详解详解)
SFINAE(替换并不是错误)机制详解详解
C—SFINAE机制详解 1. 核心概念 SFINAE(替换失败并非错误)是C模板元编程的核心机制,它规定了: 在模板参数推导/替换过程中如果某个替换导致无效代码不会引发编译错误而是从候选函数集中静默移除该模板特化 关键特性 template …...

怎么用外网打开内网的网址?如在异地在家连接访问公司局域网办公网站
什么是内网:即本地网络,私有网,内网IP,如学校局域网,家庭内网,公司内部网络等。可以简单理解为同一个路由下的几个电脑网络。 外网概念:即公网,互联网,是相对于内网而言…...
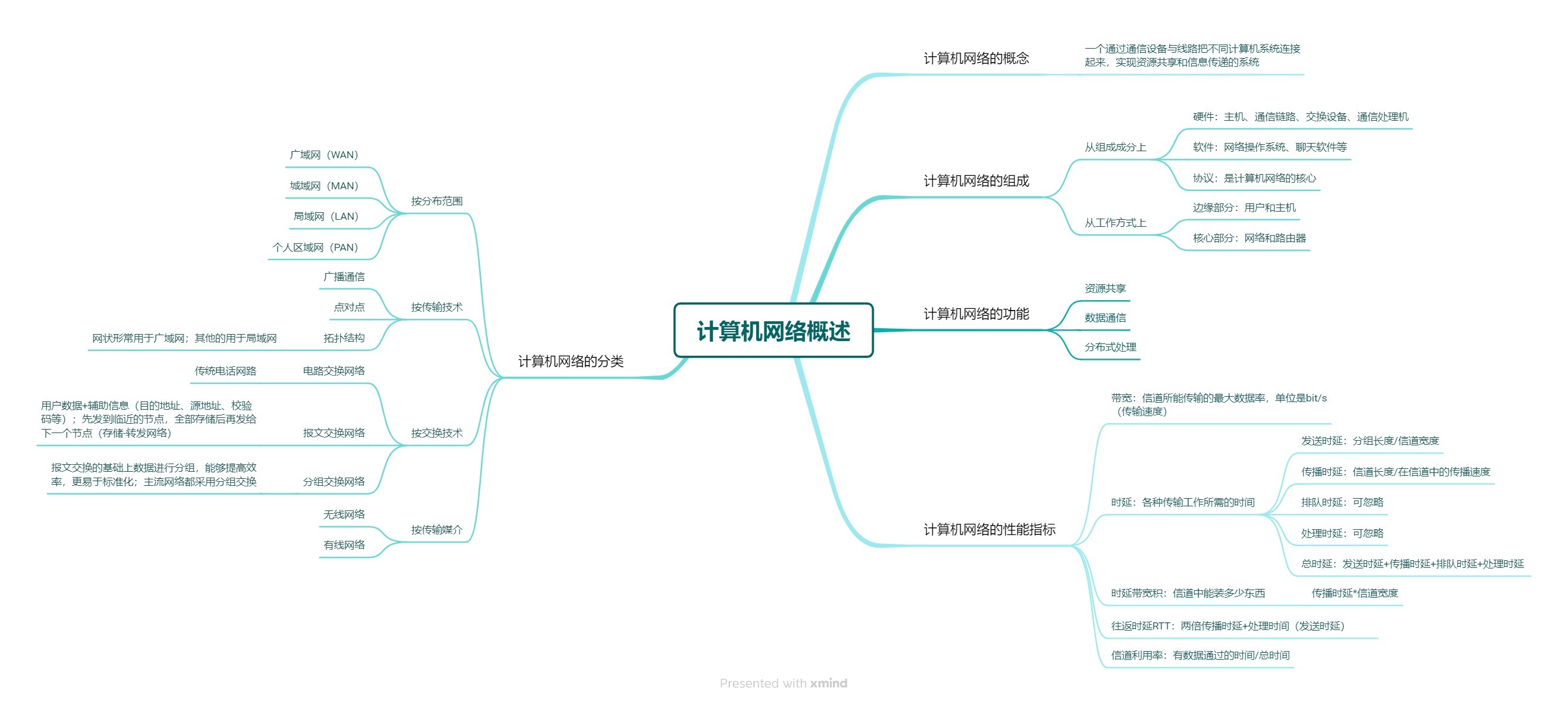
计算机网络 | 1.1 计算机网络概述思维导图
附大纲: 计算机网络的概念 一个通过通信设备与线路把不同计算机系统连接起来,实现资源共享和信息传递的系统 计算机网络的组成 从组成成分上 硬件:主机、通信链路、交换设备、通信处理机软件:网络操作系统、聊天软件等协议&…...

AI对软件工程的影响及未来发展路径分析报告
目录 第一部分:引言 研究背景与意义 报告框架与方法论 第二部分:AI对不同行业软件工程的影响分析 数字化行业 制造业 零售业 工业领域 第三部分:大厂AI软件工程实践案例分析 微软 谷歌 阿里巴巴 华为 第四部分:未来…...

redis缓存与数据库协调读写机制设计
1.读机制: 读机制没有太大的争议点,因为缓存机制的设计,就是为了更快的命中目标数据,所以读机制先天固定好了:先去读取缓存,缓存未命中再去读取数据库。 2.写机制: 写机制其实也没什么争议点…...

最悉心的指导教程——阿里云创建ECS实例教程+Vue+Django前后端的服务器部署(通过宝塔面板)
各位看官老爷们,点击关注不迷路哟。你的点赞、收藏,一键三连,是我持续更新的动力哟!!! 阿里云创建ECS实例教程 注意: 阿里云有300元额度的免费适用期哟 白嫖~~~~ 注册了阿里云账户后&#x…...

【Python】os模块
目录 🌟 前言🏗️ 技术背景与价值🩹 当前技术痛点🛠️ 解决方案概述👥 目标读者说明 🧠 一、技术原理剖析📊 核心架构图解💡 核心作用讲解🔧 关键技术模块说明⚖️ 技术选…...

Syslog 全面介绍及在 C 语言中的应用
Syslog 概述 Syslog 是一种工业标准的日志记录协议,用于在网络设备之间传递日志消息。它最早由 Eric Allman 在 1980 年代为 BSD Unix 开发,现在已成为系统和网络管理的重要组成部分。Syslog 协议允许设备将事件消息发送到中央服务器(称为 sy…...

windows中Redis、MySQL 和 Elasticsearch启动并正确监听指定端口
Redis:在 localhost 上启动,并监听端口 6379 MySQL:在 localhost 上启动,并监听端口 3306 Elasticsearch:在 127.0.0.1 上启动,并监听端口 9300 1. Redis 确保 Redis 在 localhost 上启动并监听端口 6379…...
