由sigmod权重曲线存在锯齿的探索
深度学习的知识点,一般按照执行流程,有 网络层类型,归一化,激活函数,学习率,损失函数,优化器。如果是研究生上课学的应该系统一点,自学的话知识点一开始有点乱。
一、激活函数Sigmod下的权重曲线
先开始第一个知识点激活函数的探索,说到激活函数,它是干嘛的, y=f(w*x+b)。这y就是激活函数。那本文研究的是sigmod这个激活函数权重曲线为何出现锯齿?
首先大家熟悉下,sigmod函数,见下图,特点是什么? y值范围(0,1),x在(-5,5)之间呈现线性特征。
![]()
然后不废话,上代码,先看看锯齿的效果。
import torch
import matplotlib.pyplot as pltmodel = torch.nn.Sequential(torch.nn.Linear(1,1,bias=False),# torch.nn.BatchNorm1d(1),torch.nn.Sigmoid()
)# torch.nn.init.xavier_normal_(model[0].weight)X=torch.tensor([[10.0],[2.0],[11.0],[21.0]])
Y=torch.tensor([[0.9],[0.2],[0.92],[0.987]])optimizer = torch.optim.SGD(model.paramters(),lr=1)# 使用动量的SGD
optimizer = torch.optim.SGD(model.paramters(),lr=1,momentum=0.9)weight_history=[]
for step in range(100):optimizer.zero_grad()y_pred=model(X)loss = (y_pred-Y).pow(2).mean()loss.backward()optimizer.step()weight_history.append(model[0].weight.item())plt.plot(weight_history,'-',label='Sigmoid',color='orange')
plt.xlabel('Training Step')
plt.ylabel('Weight Value')
plt.title('Sigmoid Activation:Weight Oscillation')
plt.legend()
plt.savefig('juchi.jpg')二、代码解析-kaiming均匀分布
我们先来看 torch.nn.Linear(1,1,bias=False)这句,这是一个线性函数,y=wx+b;
那么w和b为多少呢? bias为空,w呢,随机取值,但是默认符合kaiming均匀分布。
这个分布的范围呢?[-根号(1/特征数),根号(1/特征数)]。为何要这样搞,之前大伙确实随机权重,但是发展到一定阶段,发现规律了,如果这些权重符合某种分布,就能更好稳定训练。(对了,什么叫稳定训练,就是各层数据差异别太大,每一层的方差差不多的时候最好)
Kaiming初始化如何维持输入分布稳定?大家想想,对于y=f(wx+b);x是输入不能变的,激活函数也不能变。但是w可变的,通过改w可以使下一层稳定。
他让var(就是方差), var(x)=var(y)。然后var(y)=n_feautures*var(w)*var(x)。从而算出var(w)。然后均匀分布方差是 (b-a)平方/12。最终算出均匀分布的边界值(a,b)。说那么多就是为了算出均匀分布的边界值,然后才能随机嘛
三、产生锯齿的原因
产生锯齿的原因有很多种,例如学习率,数据值分布。今天我们探究的是非零中心性这个原因
Sigmoid的输出恒为正,可能导致后续层的权重梯度同号(如全正或全负),迫使优化路径呈“Z”字形调整,产生锯齿。
具体说明如下:
假设某全连接层的权重为 W,输入为 a(来自Sigmoid激活),输出为 z=W⋅a+b,损失函数为 L。根据链式法则,权重的梯度为:∂W/∂L=∂z/∂L⋅∂W/∂z=δ⋅a
其中:
- δ=∂z/∂L 是反向传播的误差项,
- a 是Sigmoid的输出,恒为正(a>0)。
关键点:梯度的符号由 δ 决定,而 δ 在反向传播中可能保持同号(全正或全负)。啥意思呢,就是这次梯度大了,然后反向时变小一点,然后下一次又小了,需要变大一点。
四、怎么解决呢?
1、入参归一化
torch.nn.BatchNorm1d(1),把数据搞成 均值为0,方差为1。这中学就学过吧。归一化的作用一句话讲,在下一层改变sigmoid输出的恒大于0的值,就是把x都变了,变成有负数了
2、使用动量的SGD
optimizer = torch.optim.SGD(model.paramters(),lr=1,momentum=0.9)
动量,白话讲,就是记住历史的变化,并非只依靠当前的,所以震荡小。好理解吧,就是船大不好掉头,船小好掉头。老外尽整一些新名词唬人。
3、换个方法,Tanh(),不用sigmod
但是这个具体看业务,并一定就能换
相关文章:

由sigmod权重曲线存在锯齿的探索
深度学习的知识点,一般按照执行流程,有 网络层类型,归一化,激活函数,学习率,损失函数,优化器。如果是研究生上课学的应该系统一点,自学的话知识点一开始有点乱。 一、激活函数Sigmod…...

二、OpenCV图像处理-图像处理
目录 1、连通性 2、形态学操作 2.1腐蚀和膨胀 2.2开闭运算 2.3礼帽和黑帽 2.4总结 3、图像平滑 3.1图像噪声 3.2均值滤波 3.3高斯滤波 3.4中值滤波 3.5总结 4、直方图 4.1直方图的原理与显示 4.2掩膜的应用 4.3直方图均衡化 4.4自适应均衡化 4.5总结 5、边缘…...

UPS的工作原理和UPS系统中旁路的作用
UPS(不间断电源)根据工作原理和适用场景的不同,主要分为以下三种类型,每种类型的特点和适用场景如下: 1. 后备式UPS(Offline/Standby UPS) 工作原理: 正常供电时,负载直接…...

麒麟系统 Linux(aarch64处理器)系统java项目接入海康SDK问题
1. 麒麟系统部署海康摄像头时的 JNA 链接错误, 海康提供的jna sdk版本太低,需升级版本4.5及以上,把集成的Structure 替换成以下类 public class SDK_Structure extends Structure {protected List<String> getFieldOrder() {List<St…...

深入理解数组索引:原理、应用与优化
在编程中,数组是一种最基本且广泛使用的数据结构。而数组索引则是访问数组元素的关键机制。本文将深入探讨数组索引的原理、应用以及优化方法,帮助读者更好地理解和使用数组索引。 一、数组索引的基本原理 数组是一种线性数据结构,它将一组…...

【洛谷P9303题解】AC- [CCC 2023 J5] CCC Word Hunt
在CCC单词搜索游戏中,单词隐藏在一个字母网格中。目标是确定给定单词在网格中隐藏的次数。单词可以以直线或直角的方式排列。以下是详细的解题思路及代码实现: 传送门: https://www.luogu.com.cn/problem/P9303 解题思路 输入读取与初始化&…...

Python图片格式批量转换器教程
📚 前言 编程基础第一期《11-30》-- 在图像处理工作中,我们经常需要将大量图片从一种格式转换为另一种格式。本教程将介绍如何使用Python的Pillow库开发一个简单但功能强大的图片格式批量转换器,帮助你高效处理图片格式转换任务。 目录 &…...

从公开到私密:重新思考 Web3 的数据安全
去中心化存储是 Web3 的基石之一,使用户和应用能够在无需依赖中心化服务商的情况下存储数据。但自由也带来了一个重大挑战:数据安全。在一个无许可的世界中,如何确保用户文档、游戏资产或 AI 数据集等敏感内容是私密的、可控访问的࿰…...

计算机网络常见体系结构、分层必要性、分层设计思想以及专用术语介绍
计算机网络体系结构 从本此开始,我们就要开始介绍有关计算机网络体系结构的知识了。内容包括: 常见的计算机网络体系结构 计算机网络体系结构分层的必要性 计算机网络体系结构的设计思想 举例说明及专用术语 计算机网络体系结构是计算机网络课程中…...
接口自动化测试用例的编写方法
🍅 点击文末小卡片,免费获取软件测试全套资料,资料在手,涨薪更快 phpunit 接口自动化测试系列 Post接口自动化测试用例 Post方式的接口是上传接口,需要对接口头部进行封装,所以没有办法在浏览器下直接调…...

解决Docker存储空间不足问题
虚拟机磁盘扩展实战:解决Docker存储空间不足问题 问题背景 在虚拟机中运行的Linux系统上,Docker服务因根分区空间不足而无法正常运行。初始状态如下: [rootlocalhost ~]# df -h / 文件系统 容量 已用 可用 已用% 挂载点…...

基于SpringBoot的商家销售管理网站的设计与实现
湖南软件职业技术大学 本科毕业设计(论文) 设计(论文)题目 基于SpringBoot的商家销售管理网站的设计与实现 学生姓名 学生学号 所在学院 专业班级 校内指导教师 企业指导教师 毕业设计(论文)真实性承诺及声明 学生对毕业设计(论文)真实性承诺 本人郑重声明:所提交的毕…...
月尺度中国气候(降水+最高/低温)数据集(1952–2019))
【数据集】高分辨率(1 km)月尺度中国气候(降水+最高/低温)数据集(1952–2019)
目录 数据描述🧩 输入数据⚙️ 数据处理流程一、ChinaClim_baseline(基准气候表面)二、ChinaClim_time-series(时序气候数据)📊 评估与验证方法📤 数据下载月最低气温月最高气温python绘制代码参考论文《1 km monthly precipitation and temperatures dataset for Ch…...

word中表格拉不动以及插入图片有间距
1、word中表格插入图片始终有间隙,怎么调表格高度和宽度都消除不了间隙,如下所示: 可以在表布局—单元格边距—修改上下左右边距为0即可 2、经过上述调整后左右没有间隔了,但图片上下有间隔,直觉是行距问题,…...
)
JavaSE:面向对象进阶之接口(Interface)
JavaSE 面向对象进阶之接口(Interface) 一、接口的核心概念 接口是一种完全抽象的类型,它定义了一组方法签名(契约),但不包含方法实现。接口的核心作用是: 规范行为:强制实现类遵…...

【Java学习笔记】接口
接口 应用场景引出 一、接口的介绍 1. 接口的基本结构 interface 接口名{属性抽象方法 }引出关键字:implements 2. 子类实现接口 class a implements 接口名{}3. 接口中的属性说明:属性默认是public static final修饰的 (1)f…...
代码随想录打卡|Day50 图论(拓扑排序精讲 、dijkstra(朴素版)精讲 )
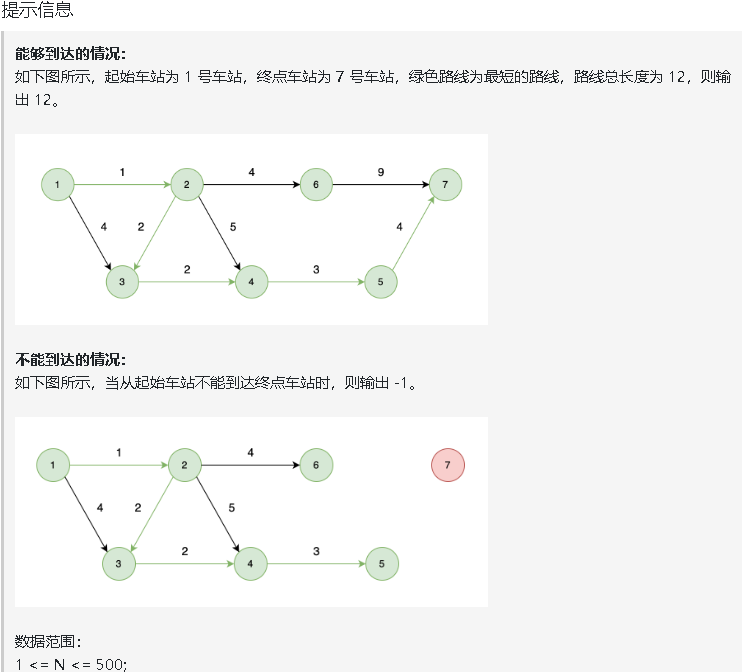
图论part08 拓扑排序精讲 代码随想录讲解链接 题目链接 思路 在这个题目之中,个别文件的处理依赖于别的文件,因此,文件的处理顺序十分重要。我们用图来表示文件的处理顺序,文件s指向文件t,则说明如果要正确的处理文…...

Wan2.1 图生视频模型内部协作流程
Wan2.1 图生视频模型内部协作流程 flyfish Wan2.1作为一个多模态生成模型,其内部涉及多个子模型的协同工作。 1. 模型架构概览 Wan2.1主要由以下核心组件构成: 文本编码器:基于T5的文本理解模型,将prompt转换为语义向量图像编…...

SI24R05国产低功耗2.4GHz+125K低频唤醒SoC人员定位/畜牧业牛羊定位/资产管理定位方案芯片
目录 SI24R05简介功能框图 主要特性开发工具方案特性 SI24R05简介 Si24R05 是一款高度集成的低功耗 SOC 芯片,具有低功耗、Low Pin Count、 宽电压工作范围,集成了 13/14/15/16 位精度的 ADC、LVD、UART、SPI、I2C、TIMER、WUP、IWDG、RTC、无线收发器、…...

qt QAxWidget
QAxWidget 是 Qt 中用于嵌入 ActiveX 控件或 COM 对象的类,主要用于 Windows 平台。以下是其使用方法的详细步骤和示例: 1. 环境配置 在 .pro 文件中添加 axcontainer 模块: QT axcontainer2. 基本使用 创建控件实例 #include <QAxW…...

机器学习与深度学习04-逻辑回归02
目录 前文回顾6.正则化在逻辑回归中的作用7.特征工程是什么8.逻辑回归的预测结果如何9.什么是ROC曲线和AUC值10.如何处理类不平衡问题11.什么是交叉验证 前文回顾 上一篇文章地址:链接 6.正则化在逻辑回归中的作用 逻辑回归中,正则化是一种用于控制模…...

CQF预备知识:Python相关库 -- NumPy 基础知识 - 通用函数
文中内容仅限技术学习与代码实践参考,市场存在不确定性,技术分析需谨慎验证,不构成任何投资建议。 通用函数 另请参阅 通用函数(ufunc) 通用函数(或简称 ufunc)是一种对 ndarrays 进行逐元素操…...

基于ELK的分布式日志实时分析与可视化系统设计
目录 一、ELK平台介绍 1.ELK概述 2.Elasticsearch 3.Logstash 4.Kibana 二、部署ES群集 1.资源清单 2.基本配置 3.安装Elasticsearch(elk1上、elk2上、elk3上) 4.安装logstash(elk1上) 5.Filebeat 6.安装Kibana&#x…...

@Async 注解 走的是主线程 还是子线程呢
Asyncz注解所在的包 package org.springframework.scheduling.annotation; Async 注解在Spring框架中用于标记一个方法为异步方法。当这个方法被调用时,它不会阻塞调用线程,而是会在一个单独的线程中执行。因此,Async 注解走的是子线程&…...

前端面经 React 组件常见的声明方式
react类组件和函数式组件 函数组件返回值的内容就是要渲染的内容 函数组件使用useState更新状态 ,使用类中变量更新 常见hook 官方 : useEffect 处理副作用,请求APIuseState 更新UIuseLayout 同步更新,会阻塞进程,…...

酒店管理系统设计与实现
本科毕业设计(论文) 设计(论文)题目 酒店管理系统设计与实现 学生姓名 学生学号 所在学院 专业班级 校内指导教师 李建 企业指导教师 毕业设计(论文)真实性承诺及声明 学生对毕业设计(论文)真实性承诺 本人郑重声明:所提交的毕业设计(论文)作品是本人在指导教师的指…...

OpenCV---pointPolygonTest
一、基本概念与用途 pointPolygonTest 是 OpenCV 中用于判断点与多边形关系的重要函数,常用于: 目标检测:判断像素点是否属于检测到的轮廓区域碰撞检测:检测物体是否重叠图像分割:确定点是否在分割区域内几何分析&am…...

Qt 的简单示例 -- 地址簿
这个工程里有两个窗口,都是QWidget派生的窗口 主窗口: 1. 运用了布局,按钮控件,单行编辑框,富文本编辑框等窗口部件; 2. 运用了 QMap 类; 3. 实现了点击按钮弹出子窗口的功能,这里子…...

Linux 下 C 语言实现工厂模式
Linux 下 C 语言实现工厂模式:设计理念与实战 🧠 一、工厂模式简介什么是工厂模式?C 语言实现设计模式的挑战 🏗️ 二、实现简单工厂模式(Simple Factory)1. 定义传感器接口(device.h࿰…...

什么是DevOps的核心目标?它如何解决传统开发与运维之间的冲突?
在当今数字化转型加速的时代,DevOps 已成为软件开发领域备受瞩目的明星理念。今天,本文将聚焦于 DevOps 的核心目标,并深入探讨它如何巧妙化解传统开发与运维之间的冲突,为大家揭开 DevOps 的神秘面纱并分享实用经验。本次介绍的与…...
