德拜温度热容推导
目录
一、背景与基本假设
一、态密度的定义
二、从波矢空间出发
三、振动模式数与波矢体积关系
四、模式总数计算
五、态密度求导
六、德拜频率确定与归一化条件
二、内能表达式的推导
三、态密度代入与变量替换
四、求比热容
五、低温时()
六、高温时()
七、总结
一、背景与基本假设
-
晶体振动与声子:
固体中原子在平衡点附近做振动,这些振动量子化后称为声子,声子是固体中的能量载体。 -
总振动模式数:
一共有3N 个独立的振动模式(每个原子有三个自由度)。 -
声子频率分布:
设声子的频率从 0 到最高频率
(德拜频率),其状态密度为
,满足归一化条件:
-
德拜假设:
声子的态密度近似为:否则为零。
一、态密度的定义
在声子体系中,态密度 表示单位频率区间内,振动模式的数目密度。也就是:
g(ν)dν=频率在 [ν,ν+dν] 的振动模式数占总模式数的比例
二、从波矢空间出发
固体中的声子模式可用波矢 描述,假设晶体是三维正方形体积 V(边长 L),周期性边界条件下波矢为:
波矢空间是离散点阵,单位体积对应的态数为:
三、振动模式数与波矢体积关系
声子模式数对应波矢空间中球体体积内的点数。对于频率 ,波矢大小 k 满足声子色散关系:
其中 v 是声波速度(德拜模型假设声速为常数,线性色散),所以:
波矢空间中,所有频率小于 的模式对应 k 在半径 k 的球体内。
该球体体积为:
四、模式总数计算
由于每个波矢对应三个声子极化分支(两横波,一纵波),总模式数为:
五、态密度求导
态密度定义为频率微分:
其中 是总振动模式数。
对 求导:
因此:
六、德拜频率确定与归一化条件
德拜频率 由总振动模式数限定:
积分:
解得:
所以标准化后的态密度:
二、内能表达式的推导
声子为玻色子,其在频率为 的振动模式上的平均能量为:
这是单个谐振子的平均能量(零点能不计,因为不随温度变化不贡献比热)。
则所有声子模式的总能量为所有模式的平均能量乘以模式总数:
三、态密度代入与变量替换
代入态密度:
定义无量纲变量:
积分上限:
其中德拜温度定义为:
代入后:
内能表达式变为:
整理:
因为 ,所以
最终内能表达式:
四、求比热容 

比热容定义为:
对U 关于 T 求导,注意积分上限依赖 T,用莱布尼茨积分法则:
其中:
而
且
代入:
注意到:
通过积分分部和利用微分关系,最终比热容的表达式可以写成:
换成气体常数 ,对应一摩尔物质的比热容:
五、低温时( )
)
此时:
积分上限趋向无穷大,可以近似:
已知:
因此:
对一摩尔:
这就是著名的德拜低温比热律,说明低温时固体比热容随温度的三次方增长。
六、高温时( )
)
这时:
积分上限接近零,可以近似积分:
代入:
这就是经典的Dulong-Petit定律,说明高温时固体比热趋近于常数。
七、总结
-
是德拜温度,代表晶格振动的最大频率对应的温度尺度。
-
积分项体现了不同频率声子对比热的贡献。
-
低温时(
),比热近似为
。
-
高温时(
),积分上限趋近无穷,积分趋近常数,恢复到经典的
(Dulong-Petit定律)。
相关文章:
德拜温度热容推导
目录 一、背景与基本假设 一、态密度的定义 二、从波矢空间出发 三、振动模式数与波矢体积关系 四、模式总数计算 五、态密度求导 六、德拜频率确定与归一化条件 二、内能表达式的推导 三、态密度代入与变量替换 四、求比热容 五、低温时() …...

扫一扫的时候会经历哪些事
“扫一扫”功能(通常指扫描二维码或条形码)是一个看似简单但背后涉及多个步骤的过程。具体会做的事情取决于你使用的APP和扫描的码的类型(二维码最常见),但核心流程通常包括以下步骤: 启动摄像头并获取图像…...
(17))
Typescript学习教程,从入门到精通,TypeScript 泛型与类型操作详解(二)(17)
TypeScript 泛型与类型操作详解(二) 本文将详细介绍 TypeScript 中的一些高级类型特性,包括条件类型、分布式条件类型、infer 关键字、内置工具类型、类型查询、类型断言、类型细化和类型守卫等。 1. 条件类型(Conditional Type…...

【iOS】源码阅读(五)——类类的结构分析
文章目录 前言类的分析类的本质objc_class 、objc_object和NSObjectobjc_object:所有对象的基类型objc_class:类的底层结构NSObject:面向用户的根类 小结 指针内存偏移普通指针----值拷贝对象----指针拷贝或引用拷贝用数组指针引出----内存偏…...

基于CangjieMagic的RAG技术赋能智能问答系统
目录 引言 示例程序分析 代码结构剖析 导入模块解读 智能体配置详情 提示词模板说明 主程序功能解析 异步聊天功能实现 检索信息展示 技术要点总结 ollama 本地部署nomic-embed-text 运行测试 结语 引言 这段时间一直在学习CangjieMagic。前几天完成了在CangjieMa…...

算力租赁革命:弹性模式如何重构数字时代的创新门槛
一、算力革命:第四次工业革命的核心驱动力 在科技飞速发展的当下,我们正悄然迎来第四次工业革命。华为创始人任正非在一场程序设计竞赛中曾深刻指出,这场革命的基础便是大算力。随着 5G、人工智能、大数据、物联网等信息技术的迅猛发展&am…...

图论回溯
图论 200.岛屿数量DFS 给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。此外ÿ…...

使用arthas热替换在线运行的java class文件
如果我们在线的系统有问题,但又无法停机进行发版或者仅仅改了一个java文件需要验证一下功能是否正常,这时可以使用arthas的在线热替换功能来做class文件的在线变更。 1.运行java -jar arthas-boot.jar,启动arathas,并选择正在运行的java的进…...

RFID测温芯片助力新能源产业安全与能效提升
在“双碳”目标驱动下,新能源产业正经历爆发式增长。无论是电动汽车、储能电站还是风光发电场,设备安全与能效提升始终是行业核心命题。而温度,这个看似普通的物理参数,却成为破解这一命题的关键密码。RFID测温芯片(集…...

S32K3 工具篇9:如何在无源码情况下灵活调试elf文件
S32K3 工具篇9:如何在无源码情况下灵活调试elf文件 一,文档简介二, 功能实现2.1 代码工具准备2.2 elf修改功能实现:Fun2功能跳过2.2.1 PC越过Fun22.2.2 Fun2替换为nop 2.3 elf修改功能实现:Fun4替换Fun2入口2.3.1 link…...

Nacos 配置文件总结
Nacos 配置文件总结 文章目录 Nacos 配置文件总结1 、在 Nacos 服务端添加配置文件1. 启动Nacos Server。2. 新建配置文件。3. 发布配置集后,我们便可以在配置列表中查看相应的配置文件。4. 配置nacos数据库5. 运行 Nacos 容器6. 验证安装结果7. 配置验证 2 、在 Na…...

ASP.NET Web Forms框架识别
ASP.NET 支持三种不同的开发模式: Web Pages(Web 页面)、MVC(Model View Controller 模型-视图-控制器)、Web Forms(Web 窗体): Web Pages 单页面模式MVC 模型-视图-控制器Web Form…...

LG P4119 [Ynoi2018] 未来日记 Solution
Description 给定序列 a ( a 1 , a 2 , ⋯ , a n ) a(a_1,a_2,\cdots,a_n) a(a1,a2,⋯,an),有 m m m 个操作分两种: replace ( l , r , x , y ) \operatorname{replace}(l,r,x,y) replace(l,r,x,y):将 a l ∼ a r a_l\sim a_r …...

流程引擎选型指南
流程引擎选型指南 流程引擎是企业实现业务流程自动化(BPM)的核心组件,选择合适的流程引擎对系统架构和未来发展至关重要。以下是主流流程引擎的综合对比和选型建议。 一、主流流程引擎对比 引擎名称开源/商业BPMN支持DMN支持CMMN支持云原生支持社区活跃度学习曲线…...
诊疗方案的研究报告)
基于大模型预测带状疱疹(无并发症)诊疗方案的研究报告
目录 一、引言 1.1 研究背景与意义 1.2 研究目的与创新点 二、带状疱疹概述 2.1 病因与发病机制 2.2 流行病学特征 2.3 临床表现与诊断标准 三、大模型技术原理及应用于带状疱疹预测的可行性 3.1 大模型技术简介 3.2 应用可行性分析 四、大模型预测带状疱疹的具体方…...

哈工大计统大作业-程序人生
摘 要 本项目以“程序人生-Hellos P2P”为核心,通过编写、预处理、编译、汇编、链接及运行一个简单的Hello程序,系统探讨了计算机系统中程序从代码到进程的全生命周期。实验基于Ubuntu环境,使用GCC工具链完成代码转换,分析了预处…...

设计模式——装饰器设计模式(结构型)
摘要 文中主要介绍了装饰器设计模式,它是一种结构型设计模式,可在不改变原有类代码的情况下,动态为对象添加额外功能。文中详细阐述了装饰器模式的角色、结构、实现方式、适合场景以及实战示例等内容,还探讨了其与其他设计模式的…...
途景VR智拍APP:开启沉浸式VR拍摄体验
在数字化时代,VR技术以其沉浸式的体验逐渐走进了人们的日常生活。途景VR智拍APP作为一款集看图和拍照于一体的VR软件,为用户带来了全新的视觉体验和便捷的拍摄方式,无论是专业摄影师还是普通用户,都能轻松上手,拍出令人…...

Linux环境搭建MCU开发环境
操作系统版本: ubuntu 22.04 文本编辑器: vscode 开发板: stm32f103c8t6 调试器: st-link 前言 步骤一: 安装交叉编译工具链 步骤二: 创建工程目录结构 步骤三: 调试…...
)
Android高级开发第一篇 - JNI(初级入门篇)
文章目录 Android高级开发JNI开发第一篇(初级入门篇)🧠 一、什么是 JNI?✅ 为什么要用 JNI? ⚙️ 二、开发环境准备开发工具 🚀 三、创建一个支持 JNI 的 Android 项目第一步:创建新项目项目结构…...

Kubernetes RBAC权限控制:从入门到实战
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言:为什么需要RBAC? 在Kubernetes集群中,权限失控是导致安全漏洞的核心原因之一。试想以下场景: 开发…...

python实战项目71:基于Python的US News世界大学排名数据爬取
python实战项目71:基于Python的US News世界大学排名数据爬取 一、项目背景1.1 研究意义1.2 技术背景1.3 应用场景二、爬虫系统设计与实现2.1 分析页面、寻找数据真实接口2.2 发送请求,获取响应内容2.3 提取数据2.4 保存数据三、完整代码四、总结与展望一、项目背景 1.1 研究…...
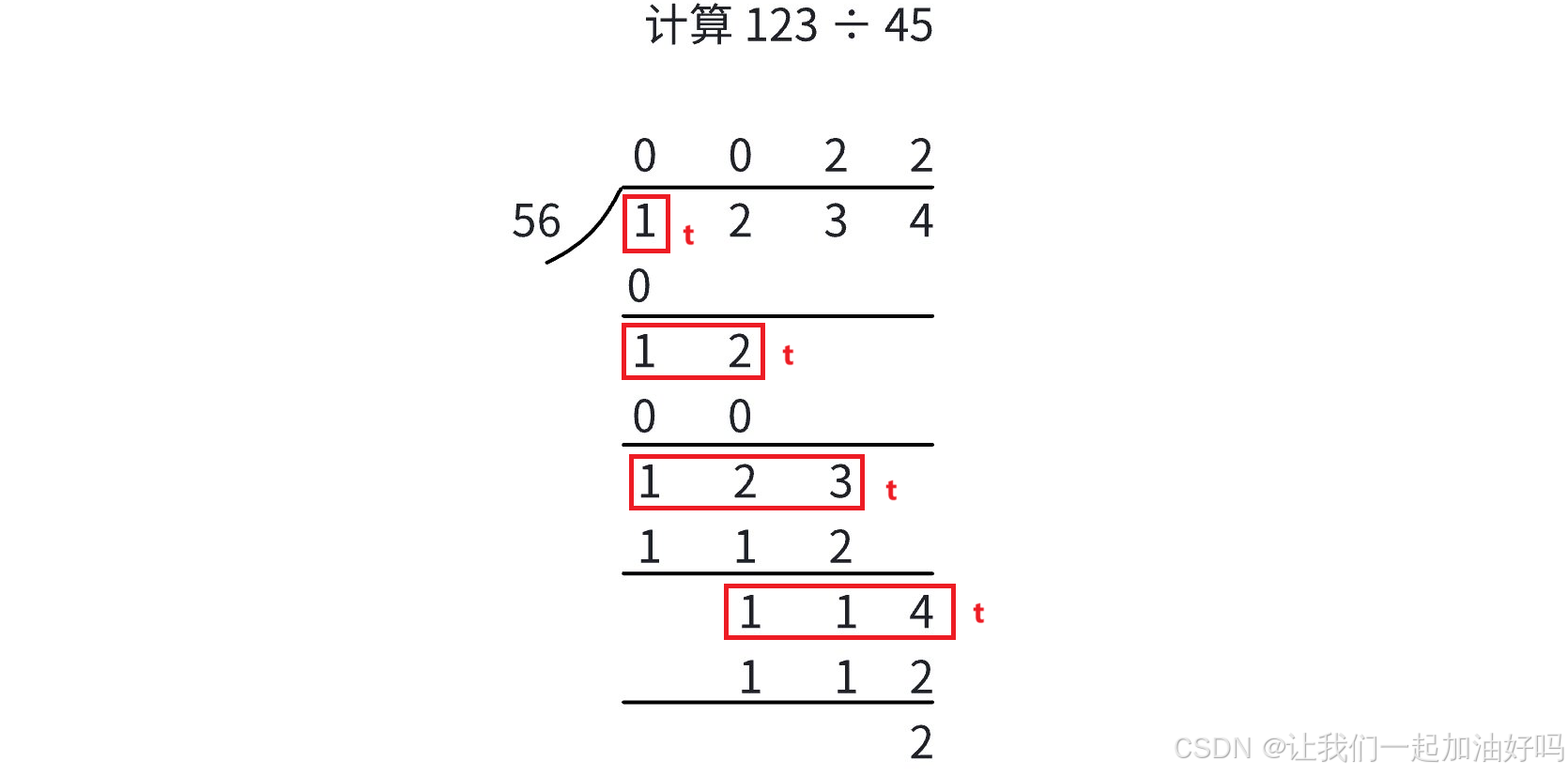
【基础算法】高精度(加、减、乘、除)
文章目录 什么是高精度1. 高精度加法解题思路代码实现 2. 高精度减法解题思路代码实现 3. 高精度乘法解题思路代码实现 4. 高精度除法 (高精度 / 低精度)解题思路代码实现 什么是高精度 我们平时使用加减乘除的时候都是直接使用 - * / 这些符号,前提是进行运算的数…...

跨平台开发框架electron
桌面端开发框架有很多,比如C#的WPF和Winform,Dart的Flutter,JS的Electron,Rust的Tauri。 目前应用比较广的是Electron,比如我们常见的开发工具VsCode,就是基于Electron开发的。 所以这篇文章我们就来聊聊Electron。 简…...

Windows最快速打开各项系统设置大全
目录 一、应用背景 二、设置项打开方法 2.1 方法一界面查找(最慢) 2.2 方法二cmd命令(慢) 2.3 方法三快捷键(快) 2.4 方法四搜索栏(快) 2.5 方法五任务栏(最快&am…...

嵌入式编译工具链熟悉与游戏移植
在自己的虚拟机Ubuntu系统下,逐步编译 mininim源码(波斯王子重制开源版) 指令流程 sudo apt-get remove liballegro5-dev liballegro-image5-dev \liballegro-audio5-dev liballegro-acodec5-dev liballegro-dialog5-dev sudo apt-get install automak…...

DeepSeek-R1-0528,官方的端午节特别献礼
DeepSeek:端午安康!刻在国人骨子里的浪漫 2025 年 05 月 28 日 | DeepSeek 端午特别献礼 当粽叶飘香时,DeepSeek 悄然带来一份节日惊喜 版本号 DeepSeek-R1-0528 正式上线 官方赋予它的灵魂是: 思考更深 推理更强 用户通过官网…...

LNMP环境中php7.2升级到php7.4
以下是 CentOS 7 上从 PHP 7.2 升级到 PHP 7.4 的详细步骤,结合知识库中的方法和注意事项: 1.备份现有环境 #备份 PHP 配置文件 cp /etc/php.ini /etc/php.ini.bak cp -r /etc/php.d /etc/php.d.bak#备份网站文件和数据库 tar -czvf website_backup.tar…...

001 flutter学习的注意事项及前期准备
在学习flutter之前,还需要进行一些初始的配置,然后才可以学习flutter 1.安装flutter 国内官网:https://flutter.cn 国际官网:https://flutter.dev 安装完成后,按照官网上面的操作步骤进行配置…...

FactoryBean 接口
Spring 框架中 FactoryBean 接口的特性,这是 Spring 提供的一种特殊机制,用于创建和管理复杂 Bean。让我通过示例和解释帮您理解这个概念。 一、FactoryBean 是什么? FactoryBean 是 Spring 框架提供的一个工厂接口,用于创建复杂…...
