【基础算法】高精度（加、减、乘、除）

什么是高精度

我们平时使用加减乘除的时候都是直接使用 + - * / 这些符号，前提是进行运算的数字在一定的范围之内。一旦这个数字非常大的时候，比如 $10^{10086}$ 这个样一个天文数字，普通的 int、long long 这些类型根本容不下它，像用它进行运算就更不可能了，所以这个时候我们就需要用到高精度算法来计算加减乘除。

高精度算法的核心有两步：

1. 先用字符串读入这个数，然后用数组逆序存储该数的每⼀位；

2. 利用数组，模拟小学就学过的加减乘除竖式运算过程。

---

1. 高精度加法

【题目链接】

P1601 A+B Problem（高精） - 洛谷

【题目描述】

高精度加法，相当于 a+b problem，不用考虑负数。

【输入格式】

分两行输入。$a,b\le 10^{500}$。

【输出格式】

输出只有一行，代表 $a+b$ 的值。

【示例一】

输入

1
1

输出

2

【示例二】

输入

1001
9099

输出

10100

【说明/提示】

$20\%$ 的测试数据，$0\le a,b\le 10^9$；

$40\%$ 的测试数据，$0\le a,b\le 10^{18}$。

---

解题思路

1. 先用字符串读入这个数，然后用数组逆序存储该数的每⼀位

我们可以在全局上设置三个数组 a[], b[], c[]，分别用于存储加法运算的左操作数、右操作数以及左后的结果的每一位（逆序）。比如 $456+789=1245$，对应 a[] = {6, 5, 4}, b = {9, 8, 7}, c = {5, 4, 2, 1}。同时，设置三个变量 la, lb, lc 用于记录数字的长度。

const int N = 1e6 + 10;
int a[N], b[N], c[N];
int la, lb, lc;

为什么要逆序？这是因为我们在人为计算竖式的时候是按照从个位到最高位去计算的，相当于逆序计算。当我们逆序存储后之后在模拟竖式计算的过程中就可以顺序遍历数组进行操作。

有了这几个变量之后就可以存储数字了，这个过程中，字符串的最后一位应存储在数组的第一位，以此类推。注意字符串中的每一位存储的是字符，而数组中存储的是数，所以在搬运各个位的时候要减去 '0' 转化成对应的数字。

string x, y;
cin >> x >> y;
la = x.size(), lb = y.size(), lc = max(la, lb); // 这里先暂时写成max(la, lb)
for(int i = 0; i < la; ++i) a[la - 1 - i] = x[i] - '0';
for(int i = 0; i < lb; ++i) b[lb - 1 - i] = y[i] - '0';

2. 利用数组，模拟小学就学过的加减乘除竖式运算过程

用循环遍历数组，填写 c[] 中的每一位。

for(int i = 0; i < lc; ++i)
{c[i] += a[i] + b[i];  // 对应位相加，再加上进位(+=实际就是加上进位)c[i + 1] = c[i] / 10;  // 进到下一位去c[i] %= 10;  // 当前位对应的数
}

---

代码实现

#include<iostream>using namespace std;const int N = 1e6 + 10;
int a[N], b[N], c[N];
int la, lb, lc;// 高精度加法
void add(int c[], int a[], int b[])
{// 模拟竖式运算for(int i = 0; i < lc; ++i){c[i] += a[i] + b[i];  // 对应位相加，再加上进位c[i + 1] = c[i] / 10;  // 处理进位c[i] %= 10;  // 当前位对应的数}// 如果最后一位进位了，那么c的长度+1if(c[lc]) ++lc;
}int main()
{string x, y;cin >> x >> y;// 拆分每一位数字，并逆序放在数组中la = x.size(), lb = y.size(), lc = max(la, lb);for(int i = 0; i < la; ++i) a[la - 1 - i] = x[i] - '0';for(int i = 0; i < lb; ++i) b[lb - 1 - i] = y[i] - '0';// 高精度加法：c = a + badd(c, a, b);// 逆序输出for(int i = lc - 1; i >= 0; --i) cout << c[i];return 0;
}

---

2. 高精度减法

【题目链接】

P2142 高精度减法 - 洛谷

【题目描述】

高精度减法。

【输入格式】

两个整数 $a,b$（第二个可能比第一个大）。

【输出格式】

结果（是负数要输出负号）。

【示例一】

输入

2
1

输出

1

【说明/提示】

• $20\%$ 数据 $a,b$ 在 long long 范围内；
• $100\%$ 数据 $0<a,b\le 10^{10086}$。

---

解题思路

和高精度加法很类似，只不过这里要处理两个细节

1. 结果可能为负数

当 x - y 的 x 比 y 小的时候，结果为负数，我们可以交换 x 和 y 的值然后在计算的结果后加上 - 即可。

而由于 x 和 y 是字符串，所以判断 x 和 y 的 “大小” 时需要考虑两个点：

• 字符串长度长的对应的数一定更大。

• 如果字符串长度一样，那么从前往后比较每一位的字典序（直接用 < 或 > 比较即可）。

2. 可能出现前导 0

我们最终输出的数的位数由 lc 决定，如果我们让 lc 的值等于 max(la, lb) 而不做处理的话下面的运算结果就为 078 而不是 78。

所以这个时候我们就需要更新 lc，可以考虑从 c[] 数组的 c[lc - 1] 位置开始往前遍历，直到遇到第一个不是 0 的位置或者lc == 0 的时候结束，在这个过程中不断让 lc 减一。

while(lc > 1 && c[lc - 1] == 0) --lc;  // 处理前导0

注意不能是 lc > 0，因为有可能两数相等相减的最终结果为 0。

---

代码实现

#include<iostream>using namespace std;const int N = 1e6 + 10;int a[N], b[N], c[N];
int la, lb, lc;// 高精度减法
void sub(int c[], int a[], int b[])
{// 模拟竖式运算for(int i = 0; i < lc; ++i){c[i] += a[i] - b[i];  // 对应位相减，并处理借位if(c[i] < 0){c[i + 1] -= 1;  // 借位c[i] += 10;}}while(lc > 1 && c[lc - 1] == 0) --lc;  // 处理前导0
}int main()
{string x, y;cin >> x >> y;// 计算 x - y// 如果 x 对应的数比 y 对应的数小，那么交换二者，并在结果前加上负号if(x.size() < y.size()|| (x.size() == y.size() && x < y)){cout << '-';swap(x, y);}// 拆分每一位数字，并逆序放在数组中la = x.size(), lb = y.size(), lc = max(la, lb);for(int i = 0; i < la; ++i) a[la - 1 - i] = x[i] - '0';for(int i = 0; i < lb; ++i) b[lb - 1 - i] = y[i] - '0';sub(c, a, b);for(int i = lc - 1; i >= 0; --i) cout << c[i];return 0;
}

---

3. 高精度乘法

【题目链接】

P1303 A*B Problem - 洛谷

【题目描述】

给出两个非负整数，求它们的乘积。

【输入格式】

输入共两行，每行一个非负整数。

【输出格式】

输出一个非负整数表示乘积。

【示例一】

输入

1 
2

输出

2

【说明/提示】

每个非负整数不超过 $10^{2000}$。

---

解题思路

乘法也可以模拟普通竖式运算过程，但是这样会频繁地处理进位，因为我们也可以采取另一种方式：无进位相乘，相加到对应位上，最后再统一处理进位。

通过下标的对应关系我们可以发现， a[] 的第 i 个位置的数与 b[] 的第 j 个位置的数相乘恰好就加在 c[] 的第 i + j 位置上。

for(int i = 0; i < la; ++i)for(int j = 0; j < lb; ++j)c[i + j] += a[i] * b[j];

当我们相加之后，再来处理进位。

for(int i = 0; i < lc; ++i)
{c[i + 1] += c[i] / 10;c[i] %= 10;
}

同样可能出现前导 0 的问题，比如 10000 * 0，于是我们采用相同的方法处理：

while(lc > 1 && c[lc - 1] == 0) --lc;

---

代码实现

#include<iostream>using namespace std;const int N = 1e6 + 10;
int a[N], b[N], c[N];
int la, lb, lc;void mul(int c[], int a[], int b[])
{// 无进位相乘，相加到对应位上for(int i = 0; i < la; ++i)for(int j = 0; j < lb; ++j)c[i + j] += a[i] * b[j];// 处理进位for(int i = 0; i < lc; ++i){c[i + 1] += c[i] / 10;c[i] %= 10;}// 处理前导0while(lc > 1 && c[lc - 1] == 0) --lc;
}int main()
{string x, y;cin >> x >> y;la = x.size(), lb = y.size(), lc = la + lb;  // 两数相乘长度最多不超过la + lbfor(int i = 0; i < la; ++i) a[la - 1 - i] = x[i] - '0';for(int i = 0; i < lb; ++i) b[lb - 1 - i] = y[i] - '0';mul(c, a, b);for(int i = lc - 1; i >= 0; --i) cout << c[i];return 0;
}

---

4. 高精度除法 (高精度 / 低精度)

【题目链接】

P1480 A/B Problem - 洛谷

【题目描述】

输入两个整数 $a,b$，输出它们的商。

【输入格式】

两行，第一行是被除数，第二行是除数。

【输出格式】

一行，商的整数部分。

【示例一】

输入

10
2

输出

5

【说明/提示】

$0\le a\le 10^{5000}$，$1\le b\le 10^9$。

---

解题思路

由于遇到较多的一般是高精度 / 低精度，所以这里就只讲这种情况。

模拟除法的竖式运算时，实际上会用到多次除法运算，我们可以用一个变量 t 来记录每次的被除数，除出来的商放在 c[] 中的对应位置，然后更新 t，总共除 la 次。最后处理前导 0 即可。

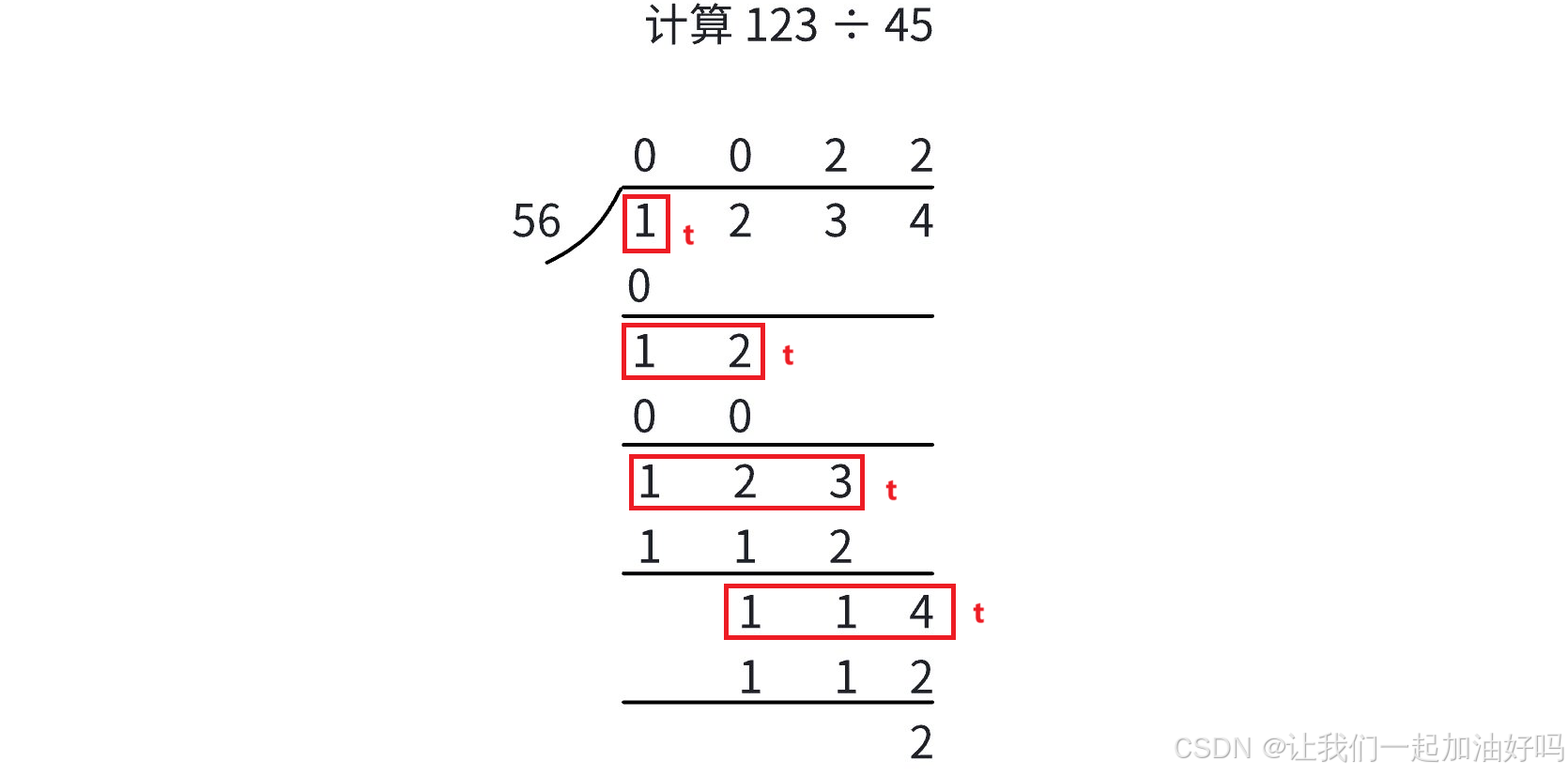
注意数据范围，b 最大是 $10^9$，而 t 可能是 b 的几倍，所以 t 可以用 long long 来存储。

---

代码实现

#include<iostream>using namespace std;typedef long long LL;const int N = 1e6 + 10;
int a[N], b, c[N];
int la, lc;// 高精度除法(高精度 / 低精度)
void div(int c[], int a[], int b)
{LL t = 0;for(int i = la - 1; i >= 0; --i){t = t * 10 + a[i];  // 计算当前的被除数c[i] = t / b;t %= b;}// 处理前导0while(lc > 1 && c[lc - 1] == 0) --lc;
}int main()
{string x; cin >> x;int b; cin >> b;la = x.size(), lc = la;for(int i = 0; i < la; ++i) a[la - 1 - i] = x[i] - '0'; div(c, a, b);for(int i = lc - 1; i >= 0; --i) cout << c[i];return 0;
}