【数据结构】——二叉树--链式结构
一、实现链式结构二叉树
二叉树的链式结构,那么从名字上我们就知道我们这个二叉树的底层是使用链表来实现的,前面我们的二叉树是通过数组来实现的,那么在其是完全二叉树的情况下,此时我们使用数组来实现就会使得其空间浪费较少,如果我们的普通的二叉树也使用数组来实现的话,那么其造成的空间浪费是非常大的。
使用链表来实现二叉树,其适用于所有的二叉树。
使用链式结构实现二叉树的方法为:链表中每个结点由三个部分组成,数据域、左孩子指针、右孩子指针。
其结构如下:

那么我们有了这个链式二叉树的结构后,那么我们要如何来实现链式结构二叉树呢?
那么我们首先就是创建二叉树的结点。
1、创建二叉树结点
结点的开辟和我们的链表是一样的,我们开辟的时候,要传的参数就是我们这个结点要存储的数据,然后我们这个结点通过二叉树结点指针返回即可 ,我们在创建的时候吗,别忘了对其初始化:

2、二叉树的遍历
二叉树的遍历分为三种方式:

1、前序遍历:先遍历根结点,然后是左结点,然后是右结点--(根左右)
如上的二叉树的前序遍历为:
A->B->D->NULL->NULL->NULL->C->E->NULL->NULL->F->NULL->NULL
2、中序遍历:先遍历左结点,然后是根结点,然后到右结点--(左根右)
如上的二叉树的中序遍历为:
NULL->D->NULL->B->NULL->A->NULL->E->NULL->C->NULL->F->NULL
3、后序遍历:先遍历左结点,然后遍历右结点,然后是根结点--(左右根)
如上的二叉树的后序遍历为:
NULL->NULL->D->NULL->B->NULL->NULL->E->F->C->A
那么我们要如何在代码中实现呢?
我们以前序遍历为例进行详细讲解:
首先我们不论是上面遍历,我们都需要这个二叉树的入口,那么我们的入口就是我们的根结点,所以我们的函数参数就是为树结点指针。
然后我们首先要进行判空,如果是空,那么我们就打印一个NULL,然后我们就终止这个函数。
如果不为空,那么我们就先将根结点的数据打印,然后我们去遍历左孩子,这是因为我们的前序遍历的顺序是根->左->右,那么我们就在这个函数中,递归调用,不过此时我们传入的参数就是根结点的左孩子了,那么其进入到左孩子后,一样还是重复的上面的操作,直到其遍历完成,然后左子树的遍历完成,那么我们就可以进入到根节点的右子树。其进入到右边子树后,还是按照根左右的顺序进行遍历即可,那么此时就可以使用我们的函数递归来实现:
其实际图解如下:

其函数栈帧如下:
 代码如下:
代码如下:

那么我们的中序遍历,又是如何来遍历的呢?我们的中序遍历的顺序为左根右,那么我们可以这样,我们进入到函数,首先还是一样,先进行判空,如果为空就打印一个NULL,然后我们就递归到这个结点的左孩子,这是,然后其就进入到递归中,直到其一直递归到其左孩子是空的,那么此时就可以打印个NULL,然后就可以打印我们的根结点的值了,然后就到我们的右边孩子,进入到右边孩子后,我们这个函数还是会按照中序遍历的顺序,先去找其左孩子。
函数如下:

同理我们的后序遍历也是如此,按照其顺序--左右根进行递归,那么我们就先递归左孩子,然后递归右孩子,然后最后打印根结点的值。
代码如下:

上面就是链式结构二叉树的三种遍历方式。
3、链式结构二叉树的插入
我们的链式结构的二叉树的插入,那么我们的入口还是树的根结点,但是其如果为空,那么此时就使其为根结点即可,然后,如果其不为空的话,那么我们要如何进行插入呢?

我们用上面的树来举例,比如我们现在要插入的树是8,那么我们的入口是根结点,那么我们将其和当前的根结点进行比较,如果比其大,那么我们就将这个数据往其左结点处走,如果这个左结点无数据,那么就直接使其为左结点,即这个要插入的结点为这个函数的左子树的根结点,那么此时我们发现当其是大于根结点的值的时候,那么我们就让第一层的根结点的左孩子指向这个要插入的结点。那么同理,当其为小于的时候,那么我们就使其指向右孩子的指针指向递归函数,函数的参数为第一层函数的右孩子。
代码如下:

不过上面的话,对于二叉搜索树其可能不允许有重复的值,所以我们上面的代码只提供链式二叉树的数据插入的思路,仅供参考。
4、求二叉树的结点个数
我们的二叉树求结点个数,没办法像链表那样进行遍历求,那么我们是否也可以和上面一样,使用函数的递归来求呢?
我们使用一个树来分析一下:

和上面一样,我们从根结点为入口,然后我们递归的话,也是分为左右子树进行递归,那么我们递归结束的条件是什么呢?其实就是这个结点是空的时候,那么说明其不是结点,那么此时就结束递归即可,回到上一层递归,那么如果其不为空,那么就说明其是一个结点,那么我们的结点数就+1,那么我们的递归就可以返回一个1,还有其左右孩子的递归。
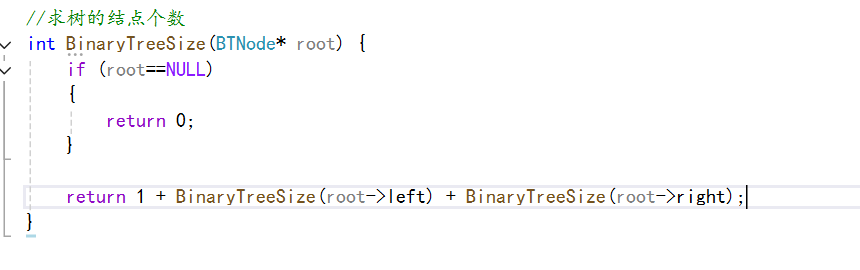
上面进行加1的原因是我们的根结点。
5、求叶子结点个数
前面我们讲过了,叶子结点就是其没有后继,即其指向左右孩子的指针都是为NULL的,那么我们这个可以作为一个条件,如果满足那么就为一个叶子结点,那么我们还是和上面一样进行递归其左右子树,如果其满足左右子孩子都是NULL,那么就返回1,如果其参数为NULL那么就返回0。
代码如下:

6、求第K层的结点个数
首先我们直到的是,如果树不为空,那么我们的第一层的结点个数为1,然后就是我们的第K层的结点个数=左子树的K-1层的结点个数+右子树的第K-1的结点个数。
那么我们可以使用函数的递归,使得k变成1的时候返回1,到空的时候也要终止递归。
代码如下:

7、求二叉树的高度
我们定义根节点的为第一层,然后我们知道,我们的二叉树的高度是左右子树中最大的一个,所以我们还是会想到使用递归左右子树的方法来进行,我们会很容易想到一个结束的条件,为空的时候返回0,然后就是我们要比较左右子树的高度,然后将大的值返回,且不要忘记+1,所以我们可以递归左右子树,分别找出左右子树的最大值,然后再进行比较。
代码如下:

8、二叉树查找值x的结点
那么我们就需要进行遍历二叉树,那么我们可以先遍历左子树,然后遍历右子树,如果在左子树没找到,那么我们再从右子树进行查找,如果没找到那么就返NULL,反之找到就返回这个结点的地址,然后如果是空树,那么就返回NULL。
代码如下:

9、链式结构二叉树的销毁
我们的销毁,那么我们还是需要遍历二叉树的每个结点,然后一个一个的进行内存释放,那么我们还是一样,对二叉树进行左右子树递归,然后当其不为空的时候就释放,为空的时候就终止函数。

可以发现我们销毁函数传递的是一个二级指针,这是因为我们要对一个指针进行修改,所以要使用地址传递才可以改变其实参的值。
二、二叉树的层序遍历
我们前面学习了二叉树的三种遍历方式,不过其是从左右子树来进行遍历,我们是否可以按照从上到下,从左到右的顺序实现二叉树的遍历呢?
要实现层序遍历,我们要借助前面学习的一个数据结构--队列。实现思路如下:
我们创建一个队列结构,其存储的是二叉树结构体,然后我们函数先将二叉树的根结点存储的数据入队,然后在进入一个循环,判断当前的队列是否为空,如果不为空,那么我们就入循环,此时我们打印队头的元素,然后将队头的元素出队,然后我们判断其是否有左孩子,如果有,那么就将其入队,然后再判断其是否有右边孩子,有的话也入队。如此反复。
代码如下:

三、判断是否完全二叉树
我们前面讲到的,完全二叉树,其除了最后一层外,其他的层次的结点都要满,然后其最后一层的结点要从左到右排序,不可以中间有空的。
那么我们可以使用我们上面的层序遍历,当我们遍历到NULL的时候,那么我们要是往后还会找到有效的结点,那么我们的这个二叉树就不是完全二叉树。
代码如下:

相关文章:

【数据结构】——二叉树--链式结构
一、实现链式结构二叉树 二叉树的链式结构,那么从名字上我们就知道我们这个二叉树的底层是使用链表来实现的,前面我们的二叉树是通过数组来实现的,那么在其是完全二叉树的情况下,此时我们使用数组来实现就会使得其空间浪费较少&a…...

TKernel模块--杂项
TKernel模块–杂项 1.DEFINE_HARRAY1 #define DEFINE_HARRAY1(HClassName, _Array1Type_) \ class HClassName : public _Array1Type_, public Standard_Transient { \public: …...

充电便捷,新能源汽车移动充电服务如何预约充电
随着新能源汽车的普及,充电便捷性成为影响用户体验的关键因素之一。传统的固定充电桩受限于地理位置和数量,难以完全满足用户需求,而移动充电服务的出现,为车主提供了更加灵活的补能方式。通过手机APP、小程序或在线平台ÿ…...

laya3的2d相机与2d区域
2d相机和2d区域都继承自Sprite。 2d相机必须作为2d区域的子节点,且2d相机必须勾选isMain才能正常使用。 2d区域下如果没有主相机,则他和Sprite无异,他的主要操作皆是针对主相机。 2d相机可以调整自己的移动范围,是否紧密跟随&a…...

2024 CKA模拟系统制作 | Step-By-Step | 19、题目搭建-升级集群
目录 免费获取题库配套 CKA_v1.31_模拟系统 一、题目 二、考点分析 1. Kubernetes 升级策略 2. 节点维护操作 3. 组件升级技术 4. 权限与访问控制 三、考点详细讲解 1. Kubernetes 升级流程 2. 组件版本兼容性 3. drain 操作深度解析 四、实验环境搭建步骤 五、总…...
)
47道ES67高频题整理(附答案背诵版)
1.ES5、ES6(ES2015)有什么区别? ES5(ECMAScript 5)和ES6(也称为ECMAScript 2015)是JavaScript语言的两个版本,它们之间有一些重要的区别和改进: let 和 const 关键字: …...

Lauterbach TRACE32专栏
官方培训视频 trace32使用技巧博文 系统崩溃分析 - vmcore 加载到 Trace32 Trace 32 离线 dump 分析环境搭建方法 内核trace分析工具入门 如何用Trace32分析内核死机 trace32调试攻略 TRACE32调试:基础调试技巧之SystemMode、SNOOPer https://cloud.tencent…...

基于 Chrome 浏览器扩展的Chroma简易图形化界面
简介 ChromaDB Manager 是基于 Chrome 浏览器扩展的一款 ChromaDB(一个流行的向量数据库)的数据查询工具。提供了一个用户友好的界面,可以直接从浏览器连接到本地 ChromaDB 实例、查看集合信息和分片数据。本工具特别适合开发人员快速查看和…...

python打卡day41
简单CNN 数据增强卷积神经网络定义的写法batch归一化:调整一个批次的分布,常用与图像数据特征图:只有卷积操作输出的才叫特征图调度器:直接修改基础学习率 一、数据增强 在图像数据预处理环节,为提升数据多样性&#x…...

IM系统的负载均衡
1.IM场景的负载均衡 2.方案总览 SDK层想要连接一个TCP网关或者WebSocket网关的方案 SDK单地址:在SDK中写死某个网关的IP或者域名,缺点是更换地址需要重新打包SDK SDK多地址:防止某一个地址嗝屁了写上多个地址用足保持高可用 暴露接口给客户端:SDK层访问接口动态获得地址 注…...

前端八股 tcp 和 udp
都是传输层协议 udp 数据报协议 不可靠面向数据包对于应用层传递的报文加上UDP首部就传给网络层 tcp 传输控制协议 可靠 会将报文分段进行传输 区别: 1.tcp 可靠 udp 不可靠 2.tcp 面向连接 三握四挥 udp 无连接 3.tcp面向字节流 udp面向报文 4.效率低 效率高…...

使用 Zabbix 监控 MySQL 存储空间和性能指标的完整实践指南
目录 引言 一、最终目标支持功能 二、监控方案设计 2.1 技术选型 2.2 设计思路 三、实现步骤 3.1 准备工作 3.11 创建 MySQL 监控账号 3.12 配置 .my.cnf 文件 3.2 编写统一脚本 3.3 配置 Zabbix Agent UserParameter 3.4 Zabbix 前端配置建议 四、总结 引言 MySQL …...

【技能拾遗】——家庭宽带单线复用布线与配置(移动2025版)
📖 前言:在家庭网络拓扑中,客厅到弱电箱只预埋了一根网线,由于已将广电的有线电视取消并改用IPTV。现在需要解决在客厅布置路由器和观看IPTV问题,这里就用到单线复用技术。 目录 🕒 1. 拓扑规划ὕ…...

异步日志监控:FastAPI与MongoDB的高效整合之道
title: 异步日志监控:FastAPI与MongoDB的高效整合之道 date: 2025/05/27 17:49:39 updated: 2025/05/27 17:49:39 author: cmdragon excerpt: FastAPI与MongoDB整合实现日志监控系统的实战指南。首先配置MongoDB异步连接,定义日志数据模型。核心功能包括日志写入接口、聚合…...

在 Android 上备份短信:保护您的对话
尽管我们的Android手机有足够的存储空间来存储无数的短信,但由于设备故障、意外删除或其他意外原因,您可能会丢失重要的对话。幸运的是,我们找到了 5 种有效的 Android SMS 备份解决方案,确保您的数字聊天和信息保持安全且可访问。…...

标题:2025海外短剧爆发年:APP+H5双端系统开发,解锁全球流量与变现新大陆
描述: 2025年出海新风口!深度解析海外短剧系统开发核心(APPH5双端),揭秘高效开发策略与商业化路径,助您抢占万亿美元市场! 全球娱乐消费模式正在剧变。2025年,海外短剧市场已从蓝海…...

解决RAGFlow(v0.19.0)有部分PDF无法解析成功的问题。
ragflow版本为:v0.19.0 1.解析的时候报错:Internal server error while chunking: Coordinate lower is less than upper。 看报错怀疑是分片的问题,于是把文档的切片方法中的“建议文本块大小”数值(默认512)调小&…...

c#基础08(数组)
文章目录 数组数组概念声明数组初始化数组赋值给数组访问数组元素 集合动态数组(ArrayList)使用foreach循环C#数组细节多维数组传递数组给函数参数数组 数组 数组概念 数组是一个存储相同类型元素的固定大小的顺序集合。数组是用来存储数据的集合,通常认为数组是一…...

嵌入式学习--江协stm32day3
这是我目前为止认为最重要的模块--TIM定时器,这里我们主要学习通用定时器 最小的计数计时单元为时基单元,包括PSC,ARR,CNT CK_PSC(Prescaler,预分频器):作用是对输入时钟信号进行分…...

docker-记录一次容器日志<container_id>-json.log超大问题的处理
文章目录 现象一、查找源头二、分析总结 现象 同事联系说部署在虚拟机里面的用docker启动xxl-job的服务不好使了,需要解决一下,我就登陆虚拟机检查,发现根目录满了,就一层一层的找,发现是<container_id>-json.l…...

4.8.1 利用Spark SQL实现词频统计
在利用Spark SQL实现词频统计的实战中,首先需要准备单词文件并上传至HDFS。接着,可以通过交互式方法或创建Spark项目来实现词频统计。交互式方法包括读取文本文件生成数据集,扁平化映射得到新数据集,然后将数据集转成数据帧&#…...
)
头歌java课程实验(Java面向对象 - 包装类)
第1关:基本数据类型和包装类之间的转换 任务描述 本关任务:实现基本数据类型与包装类之间的互相转换。 相关知识 为了完成本关任务,你需要掌握: 1.什么是包装类; 2.怎么使用包装类。 什么是包装类 在JAVA中&#x…...

经济法-7-上市公司首次发行、配股增发条件
一、首次公开发行股票条件 事项 条件存续时间,持续经营能力 持续经营3年以上的股份公司 具有持续经营能力 内部控制制度具备健全且运行良好的组织机构财务最近3年财务会计报告被出具无保留意见审计报告公司治理 1)最近3年内,发行人及…...
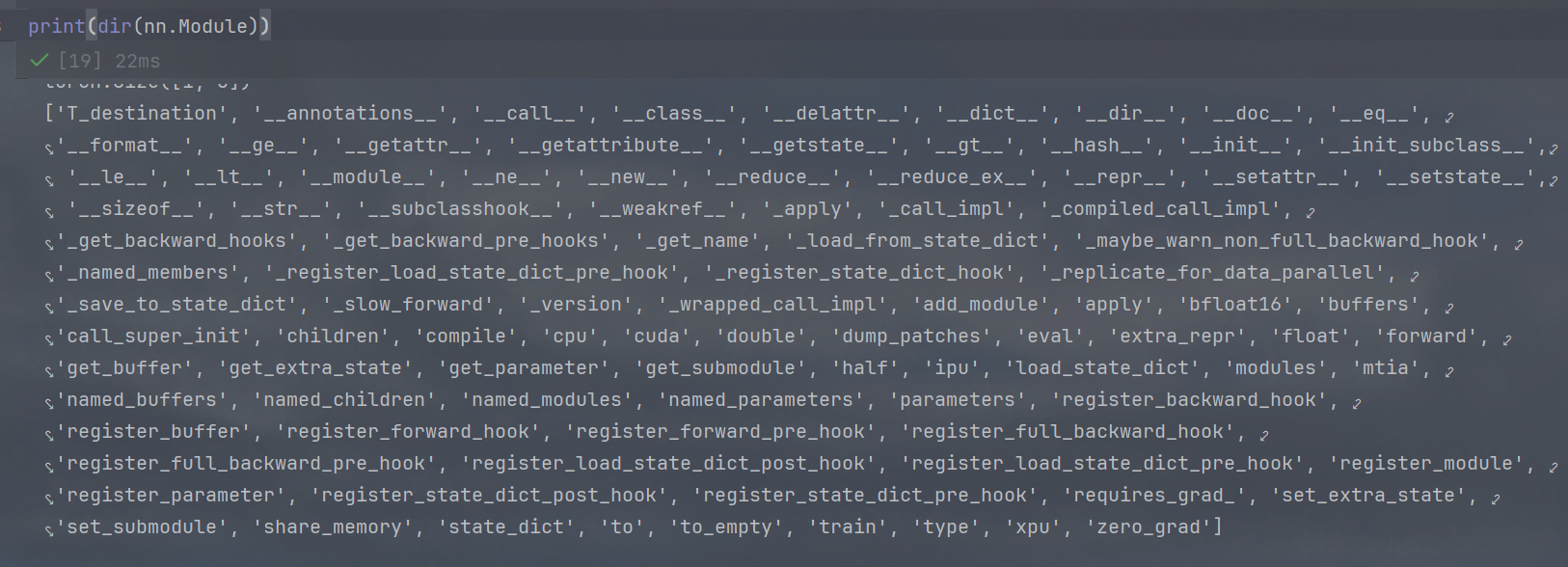
PyTorch中nn.Module详解
直接print(dir(nn.Module)),得到如下内容: 一、模型结构与参数 parameters() 用途:返回模块的所有可训练参数(如权重、偏置)。示例:for param in model.parameters():print(param.shape)named_parameters…...

Mac 每日磁盘写入量异常高
为什么你的 Mac 每日磁盘写入量异常高?深度分析与解决方案 文章目录 为什么你的 Mac 每日磁盘写入量异常高?深度分析与解决方案🔍 问题现象🕵️♂️ 六大罪魁祸首1. 系统日志疯狂输出典型场景: 2. 浏览器缓存3. Ti…...

《深入解析Go语言结构:简洁高效的工程化设计》
《深入解析Go语言结构:简洁高效的工程化设计》 引言 Go语言(Golang)由Google团队于2009年发布,专为现代分布式系统和云计算设计。其核心哲学是"简单性高于一切",通过精简的语法结构和创新的…...

[蓝桥杯]机器人塔
题目描述 X 星球的机器人表演拉拉队有两种服装,A 和 B。 他们这次表演的是搭机器人塔。 类似: A B B A B A A A B B B B B A B A B A B B A 队内的组塔规则是: A 只能站在 AA 或 BB 的肩上。 B 只能站在 AB 或 BA 的肩上。 你的…...

如何将vue2使用npm run build打包好的文件上传到服务器
要将 Vue 2 项目打包并部署到服务器上,并使用 Nginx 作为 Web 服务器,可以按照以下步骤操作: 1. 打包 Vue 2 项目 首先,确保你的 Vue 2 项目已经开发完成,并且可以在本地正常运行。然后使用以下命令进行打包…...

Ubuntu 22.04 系统下 Docker 安装与配置全指南
Ubuntu 22.04 系统下 Docker 安装与配置全指南 一、前言 Docker 作为现代开发中不可或缺的容器化工具,能极大提升应用部署和环境管理的效率。本文将详细介绍在 Ubuntu 22.04 系统上安装与配置 Docker 的完整流程,包括环境准备、安装步骤、权限配置及镜…...

动态表单开发避坑:改变input的值不会触发change事件即时修复策略-WdatePicker ——仙盟创梦IDE
原始传统模式 onchange <input onchange"未来之窗东方仙盟change(this)" oni > <script>function 未来之窗东方仙盟change(onj){console.log("未来之窗东方仙盟change",onj.value)} </script> 测试 原始传统模式 oninput <input …...
