算法打开13天

41.前 K 个高频元素

（力扣347题）

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

示例 1:

输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]

示例 2:

输入: nums = [1], k = 1
输出: [1]

提示：

• 1 <= nums.length <= 105
• k 的取值范围是 [1, 数组中不相同的元素的个数]
• 题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的

**进阶：**你所设计算法的时间复杂度 必须 优于 O(n log n) ，其中 n 是数组大小。

解题思路

1. 题目要求我们从一个整数数组 nums 中找出出现频率最高的 k 个元素。为了实现这一目标，我们可以采用以下步骤：
   1. 统计频率： 使用一个哈希表（unordered_map）来统计每个数字的出现次数。遍历数组 nums，对于每个数字，将其在哈希表中的计数加一。这样，我们可以快速得到每个数字的出现频率。
   2. 维护小顶堆： 使用一个优先队列（priority_queue）来维护频率最高的 k 个元素。优先队列的第一个元素是根节点，即堆顶元素。默认情况下，std::priority_queue 是一个大顶堆，但通过自定义比较函数 mycomparison，我们可以将其转换为小顶堆。小顶堆的特性是堆顶元素是所有元素中最小的，这正好符合我们的需求，因为我们希望在堆中保留频率最高的 k 个元素。当堆的大小超过 k 时，弹出堆顶元素（频率最小的元素），从而保证堆中始终存储的是频率最高的 k 个元素。
   3. 提取结果： 将小顶堆中的元素依次弹出，并存入结果数组。由于小顶堆的特性，弹出的顺序是频率从小到大，因此需要从后向前填充结果数组。最终，结果数组中存储的就是频率最高的 k 个元素。

单调队列与优先队列的区别

首先，我们需要明确 单调队列 和 优先队列 是两种不同的数据结构，它们的行为和用途有所不同。

单调队列

• 单调队列通常用于处理滑动窗口问题，它维护一个单调递增或单调递减的队列。
• 单调队列的第一个元素通常是当前窗口的最小值或最大值。
• 单调队列的实现通常基于双端队列（std::deque），而不是基于堆。

优先队列

• 优先队列是一种基于堆的数据结构，通常用于维护一个动态集合，使得每次可以高效地访问和删除具有最高优先级的元素。
• 优先队列的根节点（堆顶元素）是所有元素中优先级最高的元素。
• 默认情况下，std::priority_queue 是一个大顶堆，即堆顶元素是所有元素中最大的。

大顶堆的定义

在大顶堆中：

• 根节点（堆顶元素）是所有元素中最大的。
• 对于任意节点 i，其子节点的值都小于或等于节点 i 的值。

代码

// 给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。
// 你可以按 任意顺序 返回答案。
#include <iostream>
#include <vector>
#include <unordered_map>
#include <queue>
using namespace std;// 使用单调队列（基于小根堆（底层逻辑是完全二叉树）
class Solution
{
public:// 小顶堆(自定义比较函数)class mycomparison{// 重载比较运算符 std::less<T> 把默认的大顶堆变成小顶堆public://  pair<int, int>是类模板bool operator()(const pair<int, int> & lhs, const pair<int, int> & rhs){// 比较两个元素的频率，频率大的排在后面（小顶堆）return lhs.second > rhs.second;}};vector<int> topKFrequent(vector<int> &nums, int k){ // 使用哈希表统计每个数字出现的频率unordered_map<int, int> map;// 遍历数组，统计每个数字的出现次数for (int i = 0; i < nums.size(); i++){// 遍历数组，统计每个数字的出现次数map[nums[i]]++;}// 定义一个小顶堆，用于存储频率最高的 k 个元素// std::priority_queue 默认是一个大顶堆priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pri_que; // priority_queue优先队列// 遍历哈希表，将元素及其频率加入小顶堆for (unordered_map<int, int>::iterator it = map.begin(); it != map.end(); it++){// 将当前元素及其频率加入堆pri_que.push(*it);// 如果堆的大小超过 kif(pri_que.size() > k){pri_que.pop();}}// 将小顶堆中的元素依次弹出，存入结果数组vector<int> result(k);//    / 从后向前填充结果数组for(int i = k - 1;  i >= 0; i--){// 获取堆顶元素的数字部分result[i] = pri_que.top().first;// 弹出堆顶元素pri_que.pop();}// 返回结果数组return result;}
};

• 时间复杂度: O(nlogk)
• 空间复杂度: O(n)

42.二叉树的前序遍历

（力扣94题）

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

示例 1：

**输入：**root = [1,null,2,3]

输出：[1,2,3]

解释：

示例 2：

**输入：**root = [1,2,3,4,5,null,8,null,null,6,7,9]

输出：[1,2,4,5,6,7,3,8,9]

解释：

示例 3：

**输入：**root = []

输出：[]

示例 4：

**输入：**root = [1]

输出：[1]

提示：

• 树中节点数目在范围 [0, 100] 内
• -100 <= Node.val <= 100

**进阶：**递归算法很简单，你可以通过迭代算法完成吗？

解题思路

前序遍历的顺序是“根-左-右”，即先访问根节点，然后递归遍历左子树，最后递归遍历右子树。实现前序遍历可以使用递归或**非递归（栈）**的方法。

递归方法

递归方法是最直观的实现方式，利用函数调用栈来实现遍历：

1. 访问根节点：将当前节点的值加入结果向量。
2. 递归左子树：对当前节点的左子树进行前序遍历。
3. 递归右子树：对当前节点的右子树进行前序遍历。
4. 终止条件：如果当前节点为空，直接返回。

递归方法的优点是代码简洁，但可能会受到递归深度的限制。

非递归方法（栈）

非递归方法使用显式的栈来模拟递归调用：

1. 初始化栈：将根节点压入栈。
2. 循环条件：当栈不为空时，执行以下操作：
   • 弹出栈顶节点，访问其值，并将其值加入结果向量。
   • 如果右子节点不为空，将其压入栈。
   • 如果左子节点不为空，将其压入栈。
3. 终止条件：栈为空时，遍历完成。

非递归方法的优点是避免了递归调用的开销，适合处理较深的树结构

代码

#include <iostream>
#include <vector>
#include <stack>
using namespace std;
struct TreeNode
{int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(nullptr), right(nullptr) {}
};class Solution
{
public:// 递归函数void traversak(TreeNode *cur, vector<int> &vec){if (cur == nullptr){return;}vec.push_back(cur->val);    // 当前节点traversak(cur->left, vec);  // 左traversak(cur->right, vec); // 右}// 前序遍历vector<int> preorderTraversal(TreeNode *root){vector<int> result;traversak(root, result);return result;}
};
class Solution
{
public:// 前序遍历vector<int> preorderTraversal(TreeNode *root){// 定义栈stack<TreeNode *> st;// 结果集vector<int> result;// 空节点 返回空if (root == NULL){return result;}// 根节点压入栈st.push(root);while (!st.empty()){TreeNode *node = st.top(); // 根节点st.pop();result.push_back(node->val);if (node->right){// 右（空节点不入栈st.push(node->right);}if (node->left){// 左（空节点不入栈st.push(node->left);}}return  result;}
};

return 只是结束当前栈帧的执行，并返回到调用它的函数。它不会影响其他栈帧的执行

43.二叉树的后序遍历

（力扣145题）

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

示例 1：

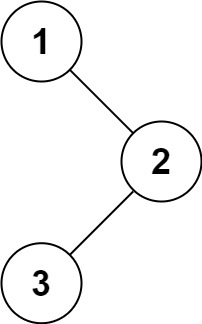
输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示：

• 树中节点数目在范围 [0, 100] 内
• -100 <= Node.val <= 100

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

解题思路

后序遍历的顺序是“左-右-根”，即先递归遍历左子树，然后递归遍历右子树，最后访问根节点。实现后序遍历可以使用递归或**非递归（栈）**的方法。

递归方法

递归方法是最直观的实现方式，利用函数调用栈来实现遍历：

1. 递归左子树：对当前节点的左子树进行后序遍历。
2. 递归右子树：对当前节点的右子树进行后序遍历。
3. 访问根节点：将当前节点的值加入结果向量。
4. 终止条件：如果当前节点为空，直接返回。

递归方法的优点是代码简洁，但可能会受到递归深度的限制。

非递归方法（栈）

非递归方法使用显式的栈来模拟递归调用：

1. 初始化栈：将根节点压入栈。
2. 循环条件：当栈不为空时，执行以下操作：
   • 弹出栈顶节点，访问其值，并将其值加入结果向量。
   • 如果左子节点不为空，将其压入栈。
   • 如果右子节点不为空，将其压入栈。
3. 反转结果集：由于栈的后进先出特性，最终结果需要反转。
4. 终止条件：栈为空时，遍历完成。

非递归方法的优点是避免了递归调用的开销，适合处理较深的树结构。

代码

#include <iostream>
#include <vector>
#include <stack>
#include <algorithm>
using namespace std;
struct TreeNode
{int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(nullptr), right(nullptr) {}
};class Solution
{
public:// 递归函数void traversak(TreeNode *cur, vector<int> &vec){if (cur == nullptr){return;}traversak(cur->left, vec);  // 左traversak(cur->right, vec); // 右vec.push_back(cur->val);    // 当前节点}// 后序遍历vector<int> postorderTraversal(TreeNode *root){vector<int> result;traversak(root, result);return result;}
};class Solution
{
public:// 后序遍历vector<int> postorderTraversal(TreeNode *root){// 定义栈stack<TreeNode *> st;// 结果集vector<int> result;// 空节点 返回空if (root == NULL){return result;}// 根节点压入栈st.push(root);while (!st.empty()){TreeNode *node = st.top(); // 根节点st.pop();result.push_back(node->val);if (node->left){// 左（空节点不入栈st.push(node->left);}if (node->right){// 右（空节点不入栈st.push(node->right);}}// 反转结果集reverse(result.begin(), result.end());return  result;}
};