[蓝桥杯]剪格子
剪格子
题目描述
如下图所示,3 x 3 的格子中填写了一些整数。

我们沿着图中的红色线剪开,得到两个部分,每个部分的数字和都是 60。
本题的要求就是请你编程判定:对给定的 m×nm×n 的格子中的整数,是否可以分割为两个部分,使得这两个区域的数字和相等。
如果存在多种解答,请输出包含左上角格子的那个区域包含的格子的最小数目。
如果无法分割,则输出 0。
输入描述
输入描述
程序先读入两个整数 m,nm,n 用空格分割 (m,n<10)(m,n<10),表示表格的宽度和高度。
接下来是 nn 行,每行 mm 个正整数,用空格分开。每个整数不大于 104104。
输出描述
在所有解中,包含左上角的分割区可能包含的最小的格子数目。
输入输出样例
示例
输入
3 3
10 1 52
20 30 1
1 2 3
输出
3
运行限制
- 最大运行时间:5s
- 最大运行内存: 64M
总通过次数: 2669 | 总提交次数: 3114 | 通过率: 85.7%
难度: 中等 标签: 2013, 省赛, 搜索
方法思路
题目要求将网格分割成两个连通区域,使得两个区域的数字和相等,并输出包含左上角格子的最小格子数目。解决思路如下:
-
检查总和:计算网格所有元素的总和。如果总和为奇数,则无法分割,输出0。
-
深度优先搜索:从左上角格子开始DFS,探索所有四连通区域:
-
剪枝优化:若当前区域和超过总和一半或格子数已超过最小解,则回溯。
-
解验证:当区域和等于总和一半时,检查剩余部分是否连通(使用BFS)。
-
-
连通性检查:对剩余部分进行BFS,验证其连通性。
-
结果输出:记录满足条件的最小格子数,若未找到解则输出0。
#include <iostream> #include <vector> #include <queue> #include <climits> using namespace std;int m, n; vector<vector<int>> grid; vector<vector<bool>> visited; int total = 0; int min_count = INT_MAX;// 方向数组:上、右、下、左 int dx[4] = {-1, 0, 1, 0}; int dy[4] = {0, 1, 0, -1};// 检查剩余部分连通性 bool check_connectivity(int count) {int total_count = n * m;int remain_count = total_count - count;if (remain_count == 0) return true;// 找到第一个剩余格子int start_i = -1, start_j = -1;for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (!visited[i][j]) {start_i = i;start_j = j;break;}}if (start_i != -1) break;}// BFS遍历剩余格子vector<vector<bool>> temp_vis(n, vector<bool>(m, false));queue<pair<int, int>> q;q.push({start_i, start_j});temp_vis[start_i][start_j] = true;int cnt = 1;while (!q.empty()) {auto [x, y] = q.front();q.pop();for (int k = 0; k < 4; k++) {int nx = x + dx[k];int ny = y + dy[k];if (nx >= 0 && nx < n && ny >= 0 && ny < m && !visited[nx][ny] && !temp_vis[nx][ny]) {temp_vis[nx][ny] = true;cnt++;q.push({nx, ny});}}}return cnt == remain_count; }// 深度优先搜索 void dfs(int i, int j, int sum, int count) {// 剪枝:超过总和一半或已找到更优解if (sum > total / 2) return;if (count >= min_count) return;// 找到可行解并检查剩余部分连通性if (sum == total / 2) {if (check_connectivity(count)) {min_count = min(min_count, count);}return;}// 四方向扩展for (int k = 0; k < 4; k++) {int ni = i + dx[k];int nj = j + dy[k];if (ni >= 0 && ni < n && nj >= 0 && nj < m && !visited[ni][nj]) {visited[ni][nj] = true;dfs(ni, nj, sum + grid[ni][nj], count + 1);visited[ni][nj] = false;}} }int main() {cin >> m >> n;grid.resize(n, vector<int>(m));visited.resize(n, vector<bool>(m, false));// 读入网格并计算总和for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {cin >> grid[i][j];total += grid[i][j];}}// 总和为奇数则无解if (total % 2 != 0) {cout << 0 << endl;return 0;}// 从左上角开始DFSvisited[0][0] = true;dfs(0, 0, grid[0][0], 1);// 输出结果if (min_count == INT_MAX) {cout << 0 << endl;} else {cout << min_count << endl;}return 0; }代码解释
-
输入处理:
-
读取网格的行数
n和列数m。 -
使用二维向量
grid存储网格元素,visited标记访问状态。 -
计算网格元素总和
total。
-
-
总和检查:
-
若总和为奇数,直接输出
0并结束(无法分割)。
-
-
深度优先搜索:
-
从左上角
(0,0)开始DFS,标记该格子已访问。 -
剪枝:当前区域和超过
total/2或格子数超过最小解时回溯。 -
解验证:当区域和等于
total/2时,调用check_connectivity检查剩余部分连通性。
-
-
连通性检查:
-
使用BFS遍历剩余格子:
-
统计剩余格子数量
remain_count。 -
从第一个剩余格子开始BFS,统计连通格子数
cnt。 -
若
cnt == remain_count则剩余部分连通。
-
-
-
结果输出:
-
若找到解,输出最小格子数
min_count。 -
若未找到解,输出
0。
-
示例说明
对于输入样例:
3 3 10 1 52 20 30 1 1 2 3
-
总和:120(
total/2 = 60)。 -
可行解:格子
(0,0)=10、(1,0)=20、(1,1)=30(和=60)。 -
剩余部分:其他格子连通(通过BFS验证)。
-
最小格子数:3(输出结果)。
相关文章:

[蓝桥杯]剪格子
剪格子 题目描述 如下图所示,3 x 3 的格子中填写了一些整数。 我们沿着图中的红色线剪开,得到两个部分,每个部分的数字和都是 60。 本题的要求就是请你编程判定:对给定的 mnmn 的格子中的整数,是否可以分割为两个部…...

明远智睿SSD2351开发板:语音机器人领域的变革力量
在人工智能快速发展的今天,语音机器人逐渐成为人们生活和工作中的得力助手。明远智睿SSD2351开发板凭借强大性能与丰富功能,为语音机器人的发展注入新动力,成为该领域的变革力量。 SSD2351开发板的四核1.4GHz处理器具备强劲的运算性能&#x…...
)
Mybtais框架各配置文件主要内容详解(一)
前言: Mybatis由ibatis框架演变而来——2010 年,iBATIS 框架正式更名为 MyBatis,并捐赠给 Apache 软件基金会,开启了开源社区驱动的发展之路。 Mybatis处于MVC三层架构的Model层,是一款优秀的半自动orm框架ÿ…...

Co-IP—验证蛋白互作的不二之选
蛋白互作在细胞生命活动中起着至关重要的作用,并在不同的时空层面上参与多种细胞活动,因此研究蛋白互作对于理解分子调控网络至关重要。而在植物中筛选到潜在的互作蛋白后,大多数情况下,获得表达两种蛋白的稳定转化植株费时又费力…...

数据可视化(第4、5、6次课)
Matplotlib 折线图 import numpy as np import matplotlib.pyplot as plt import matplotlib # 配置中文格式——保证图中出现中文的时候不会乱码 matplotlib.rcParams[font.sans-serif][SimHei] matplotlib.rcParams[axes.unicode_minus]False # 绘图 x np.linspace(0,2*np…...

DAY 18 推断聚类后簇的类型
目录 DAY 18 推断聚类后簇的类型1.推断簇含义的2个思路:先选特征和后选特征2.通过可视化图形借助ai定义簇的含义3.科研逻辑闭环:通过精度判断特征工程价值作业:参考示例代码对心脏病数据集采取类似操作,并且评估特征工程后模型效果有无提升。…...

结合源码分析Redis的内存回收和内存淘汰机制,LRU和LFU是如何进行计算的?
Redis 内存回收 1. 过期 key 处理 Redis 之所以性能强,最主要的原因就是基于内存存储。然而单节点的 Redis 其内存大小不宜过大,会影响持久化或主从同步性能。我们可以通过修改配置文件来设置Redis的最大内存: 当内存使用达到上限时&#…...

ESG体系
文字来自腾讯元宝 ESG是什么? ESG体系是一套综合评估企业在环境(Environmental)、社会(Social)和治理(Governance) 三个维度表现的非财务绩效标准,旨在衡量企业可持续发展能力和长期…...

基于 KubeKey 3.1.9,快速部署 K8s 1.33.0 高可用集群
作者:丁鑫磊,云原生运维工程师,专注于 KubeSphere 与 K8s 的深度应用,致力于自动化方向的探索与实践。热衷于挖掘 KubeSphere 的运维潜力,借助其简化 K8s 操作,提升运维效率,为企业云原生转型推…...

华为深度学习面试手撕题:手写nn.Conv2d()函数
题目 只允许利用numpy包,实现Pytorch二维卷积函数nn.Conv2d() 解答 此代码考察二维卷积的概念,详见: 6.2. 图像卷积 — 动手学深度学习 2.0.0 documentation 6.3. 填充和步幅 — 动手学深度学习 2.0.0 documentation 6.4. 多输入多输出通…...
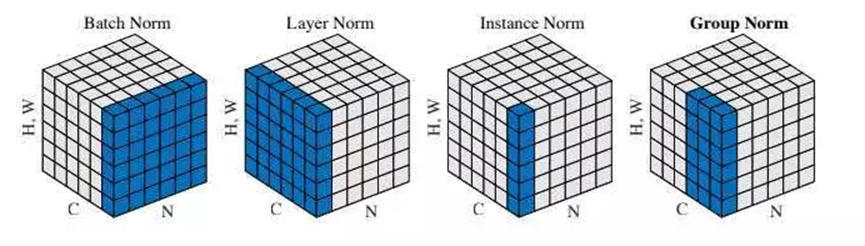
归一化相关
归一化相关问题 归一化方式Batch NormalizationLayer NormalizationInstance NormalizationGroup NormalizationRMSNorm(Root Mean Square Layer Normalization):RMSNorm 和 LayerNorm区别?归一化方式 Batch Normalization 在每一层的输入进行归一化处理,使其在每个批次内…...

STM32Cubemx-H7-17-麦克纳姆轮驱动
前言 --末尾有总体的.c和.h 本篇文章把麦克纳姆轮的代码封装到.c和.h,使用者只需要根据轮子正转的方向,在.h处修改定义方向引脚,把轮子都统一正向后,后面的轮子驱动函数就可以正常了,然后直接调用函数驱动即可。 设…...

机器学习算法-逻辑回归
今天我们用 「预测考试是否及格」 的例子来讲解逻辑回归,从原理到实现一步步拆解,保证零基础也能懂! 🎯 例子背景 假设你是班主任,要根据学生的「学习时间」预测「是否及格」,手上有以下数据:…...

Office 2024免费下载 安装包
各位办公小能手们,你们知道吗?咱们日常办公经常会用到一个超厉害的软件套件,那就是Office,它全称Microsoft Office,是微软公司开发的。这玩意儿能大大提升个人和团队的办公效率,像文档处理、数据分析、演示…...
)
Linux云计算训练营笔记day18(Python)
# 猜数字游戏: 程序生产一个 1-100的随机数 # 让用户重复去猜测, 直到猜对为止 # 如果用户输入的数字 大于 随机生成的数字 提示 大了 # 如果用户输入的数字 小于 随机生产的数字 提示 小了 # 否则 猜对了 break # 增加需求 最多猜6次,如果没有猜对,提示 你失…...

Git深入解析功能逻辑与核心业务场景流程
一、Git核心功能逻辑架构 #mermaid-svg-9tj1iCr99u6QenJM {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-9tj1iCr99u6QenJM .error-icon{fill:#552222;}#mermaid-svg-9tj1iCr99u6QenJM .error-text{fill:#552222;st…...

Opencv4 c++ 自用笔记 03 滑动条、相机与视频操作
1. 相机与视频操作 1.1 打开视频/相机 OpenCV 中 imread() 只能读取静态图像,若要读取视频文件或摄像头流,需要使用 VideoCapture 类: // 构造函数 cv::VideoCapture::VideoCapture(); cv::VideoCapture…...

LINUX528 重定向
2>&1 我的理解: 2>&1,2stderr错误输出,1stdout输出,stderr一般和stdout是分别输出(管道符只传递stdout,据元宝,stderr默认输出到终端;如果重定向符不进行2显示重定向&…...

研华工控机安装Windows10系统,适用UEFI(GPT)格式安装
主要硬件 主板:AIMB-787 、CPU:i5-6500 U盘启动工具:通过网盘分享的文件:rufus-3.20.zip 链接: https://pan.baidu.com/s/1YlFfd-_EhFHCG4sEHBQ8dQ?pwdQT12 提取码: QT12 Win10 22H2 Pro 纯净版系统:通过网盘分享…...

1、树莓派更换软件下载源
树莓派官方系统raspbian自带的是国外的软件源,在国内使用经常会遇到无法下载软件的问题。 以下是把raspbian系统(buster版本)的下载源改为阿里云软件源的方法。 1、修改sources.list文件 sudo nano /etc/apt/sources.list 将初始化中的代…...

历年中山大学计算机保研上机真题
历年中山大学计算机保研上机真题 2025中山大学计算机保研上机真题 2024中山大学计算机保研上机真题 2023中山大学计算机保研上机真题 在线测评链接:https://pgcode.cn/school 不连续1的子串 题目描述 给定一个数字 n n n,输出长度为 n n n 的 01…...

Python----目标检测(《SSD: Single Shot MultiBox Detector》论文和SSD的原理与网络结构)
一、SSD:单次多框检测器 1.1、基本信息 标题:SSD: Single Shot MultiBox Detector 作者:Wei Liu (UNC Chapel Hill), Dragomir Anguelov (Zoox Inc.), Dumitru Erhan, Christian Szegedy (Google Inc.), Scott Reed (University of Michiga…...

springboot集成websocket给前端推送消息
一般通常情况下,我们都是前端主动朝后端发送请求,那么有没有可能,后端主动给前端推送消息呢?这时候就可以借助websocket来实现。下面给出一个简单的实现样例。 首先创建一个websocketDemo工程,该工程的整体结构如下&a…...

DrissionPage SessionPage模式:轻量级HTTP请求的利器
引言 在Python自动化领域,DrissionPage以其创新的三模式设计脱颖而出。作为专为HTTP请求优化的SessionPage模式,凭借其轻量级架构和高效性能,成为API调用、数据采集等场景的首选方案。本文将深入解析SessionPage的技术特性、核心优势及典型应…...

0527漏洞原理:XSS笔记
理论知识 01 前端基础知识 1.1 HTML基础 定义:HTML(超文本标记语言)用于描述网页结构。标准结构: 内嵌脚本: <script>JavaScript代码</script>1.4 JavaScript弹窗函数 函数描述alert("文本&quo…...

智能制造之精读——RPA制造行业常见场景【附全文阅读】
RPA 在制造行业应用广泛,为企业带来显著价值,是极具潜力的智能化解决方案。它能节省成本,降低人力与管理成本;提升运营效率,减少人机交互损耗;提高质量,保障流程准确性;还能增强合规…...

spark shuffle的分区支持动态调整,而hive不支持
根据Spark官方文档,Spark Shuffle分区支持动态调整的核心原因在于其架构设计和执行模型的先进性: 1. 自适应查询执行(AQE)机制 Spark 3.0引入的AQE特性允许在运行时动态优化执行计划,包括Shuffle分区调整:…...

网络安全十大漏洞
1️⃣ 失效的访问控制(Broken Access Control) 核心问题:用户能访问本应被禁止的资源或操作 攻击案例: 修改URL参数:https://shop.com/order?user_id100 → 改为 user_id101 查看他人订单 直接访问管理员页面&#…...
)
关于uv 工具的使用总结(uv,conda,pip什么关系)
最近要开发MCP 项目,uv工具使用是官方推荐的方式,逐要了解这个uv工具。整体理解如下: 一.uv工具的基本情况 UV 是一个由 Rust 编写的现代化 Python 包管理工具,旨在通过极速性能和一体化功能替代传统工具(如 pip、vi…...

深入剖析 Docker 容器化原理与实战应用,开启技术新征程!
文章目录 前言一、为什么 是Docker ?二、Docker 容器化原理分析2.1 镜像(Image)2.2 容器(Container)2.3 仓库(Registry) 三、Docker 容器化实践3.1 Docker安装3.2 创建一个 Docker 镜像3.3 运行…...
