017搜索之深度优先DFS——算法备赛
深度优先搜索
如果说广度优先搜索是逐层扩散,那深度优先搜索就是一条道走到黑。
深度优先遍历是用递归实现的,预定一条顺序规则(如上下左右顺序) ,一直往第一个方向搜索直到走到尽头或不满足要求后返回上一个叉路口按第二个方向继续搜索,以此类推,直到所有节点都遍历到。
简单回溯
N皇后
问题描述:
设计一种算法,打印 N 皇后在 N × N 棋盘上的各种摆法,其中每个皇后都不同行、不同列,也不在对角线上。
这里的“对角线”指的是所有的对角线,不只是平分整个棋盘的那两条对角线。
原题链接
思路分析
N皇后问题是dfs的经典问题。
对于每一行,皇后都有N(N列)种放法,对于每一行遍历每一种位置,如果它与前面某一行的皇后处在同一列或同一对角线那就不能摆放在该位置;否则可以摆放在该位置,进行下一行的摆放。
vector<int>x; //存储第i行皇后所在列
vector<vector<string>>tar;
vector<string>tr;
int sum=0,s;
bool check(int k){for(int i=1;i<k;i++){if(x[k]==x[i]) return false; //判断该行的皇后是否与前面的皇后在同一列if(abs(x[k]-x[i])==k-i) return false; //判断该行的皇后是否与前面的皇后在同一对角线}return true;
}
void DFS(int t){if(t>s) { //当m>s时,该方案满足条件。sum++; //记录方案数。tar.push_back(tr);}else{for(int i=1;i<=s;i++){x[t]=i;tr[t-1]="";tr[t-1].insert(0,s,'.');tr[t-1][i-1]='Q'; //修改该行状态if(check(t)) DFS(t+1); //符合条件 开始下一行的摆放。 不合条件则摆在下一列。}}
}
vector<vector<string>> solveNQueens(int n) {s=n;x.resize(n+1);tr.resize(n);DFS(1); //从第一行开始搜索return tar;
}
路径之迷
蓝桥杯2016年国赛题
描述:

原题链接
代码
#include <bits/stdc++.h>
using namespace std;int dx[4] = { 0,1,0,-1 };
int dy[4] = { 1,0,-1,0 };
int n;
vector<int>rowCnt, colCnt;
bool allFlat = false;
vector<vector<bool>>vis;
vector<int>tar;bool checkEnd(int row, int col) {if (row != n - 1 || col != n - 1) return false;for (int i = 0; i < n; i++) {if (rowCnt[i]) return false; //有一个不为0,返回false}for (int i = 0; i < n; i++) {if (colCnt[i]) return false; //有一个不为0,返回false}allFlat = true;return true;
}bool check(int row, int col) {if (row < 0 || row >= n || col < 0 || col >= n|| vis[row][col]) return false; //越界或走到已走过的节点if (rowCnt[row] <= 0 || colCnt[col] <= 0) return false; //箭用完了return true;
}void dfs(int row, int col) {if (checkEnd(row, col) || allFlat) return; //结束for (int i = 0; i < 4; i++) {int x = row + dx[i];int y = col + dy[i];if (check(x,y)) {vis[x][y] = true;rowCnt[x]--, colCnt[y]--;tar.push_back(x * n + y); //第x行,第y列的节点编号为 x * n + ydfs(x, y);if (allFlat) return; //allFlat为true,不用继续执行了vis[x][y] = false; //回溯,还原现场rowCnt[x]++, colCnt[y]++;tar.pop_back();}}
}
int main()
{cin >> n;rowCnt = vector<int>(n);colCnt = vector<int>(n);vis = vector<vector<bool>>(n, vector<bool>(n));for (int i = 0; i < n; i++)cin >> colCnt[i];for (int i = 0; i < n; i++)cin >> rowCnt[i];vis[0][0] = 1;colCnt[0]--;rowCnt[0]--;tar.push_back(0);dfs(0, 0);for (auto i : tar) {cout << i << " ";}return 0;
}
简单正则问题
蓝桥杯2017年省赛题
问题描述
考虑一种简单的正则表达式:只由 x,(,),| 组成的正则表达式。求这个正则表达式能接受的最长字符串的长度?
例((xx|xxx)x|(x|xx))xx 能接受的最长字符串是xxxxxx,长度是6.
原题链接
思路分析
()规定了运算的优先级最高,|代表长度取max,x代表一个字符- 根据嵌套规则,设计dfs
- 自底向上画出问题的二叉树,以
((xx|xxx)x|(x|xx))xx为例

代码
#include<bits/stdc++.h>using namespace std;string s;
int k = 0;int dfs()
{int res = 0; //统计当前层可以容纳多少xwhile(k < s.size()){if(s[k] == '('){k++; //跳过左括号res += dfs(); //遇到括号,把括号中的值求出,再与res做+运算 k++; //跳过右括号}else if(s[k] == '|'){k++; //跳过 或 运算res = max(res, dfs()); //遇到或运算,把|右边的求出,再与res做max运算}else if(s[k] == ')') break; else{k++; res++; //遇到单个x,res直接加1}}return res;
}int main()
{cin >> s;cout << dfs() << endl;return 0;
}
记忆化搜索
掷骰子等于目标数的方法数
问题描述
这里有 n 个一样的骰子,每个骰子都不一样,每个骰子上都有 k 个面,分别标号为 1 到 k 。
给定三个整数 n、k 和 target,请返回投掷骰子的所有可能得到的结果中(总共有 k^n 种方式),使得骰子面朝上的数字总和等于 target的结果数。
由于答案可能很大,你需要对 109 + 7 取模。
原题链接
思路分析
枚举第n个筛子的点数为x,那么这种情况的结果数就是前 n-1个筛子点数和为target-x的结果数。
那可以很自然地想到定义dp[i][j]表示前i个筛子点数和为j的结果数,dp[i][j]=sum(dp[i-1][j-x]) , x为枚举的第i个筛子的点数。
动态规划的过程可以使用直观一点的记忆化搜索。
代码
int numRollsToTarget(int n, int k, int target) {int mod=1e9+7;vector<vector<int>>dp(n+1,vector<int>(target+1));auto dfs=[&](auto dfs,int st,int sum)->int{if(dp[st][sum]) return dp[st][sum];if(st==n){if(sum<=k){dp[n][sum]=1;return 1;}}int l=max(1,sum-(n-st)*k);int r=min(k,sum-(n-st));for(int i=l;i<=r;i++){dp[st][sum]=(dp[st][sum]+dfs(dfs,st+1,sum-i))%mod;}return dp[st][sum];};return dfs(dfs,1,target);
}
统计满足逆序对数量条件的排列数量
给你一个整数 n 和一个二维数组 requirements ,其中 requirements[i] = [endi, cnti] 表示这个要求中的末尾下标和 逆序对 的数目。
整数数组 nums 中一个下标对 (i, j) 如果满足以下条件,那么它们被称为一个 逆序对 :
i < j且nums[i] > nums[j]
请你返回 [0, 1, 2, ..., n - 1] 的 排列 perm 的数目,满足对 所有 的 requirements[i] 都满足 perm[0..endi] 中恰好有 cnti 个逆序对。
由于答案可能会很大,将它对 109 + 7 取余 后返回。
思路分析
首先将问题分解为子问题。考虑示例{n = 3, requirements = [[2,2],[0,0]] },整个排列 [0,2] 恰好要有 2 个逆序对。分情况进行讨论:
- 末尾元素为 0。由于 0 是最小元素,前面的两个元素,每个元素都会与 0 构成一对逆序对。此时,[0,1] 还需要贡献 0 对逆序对。
- 末尾元素为 1。前面的两个元素中,2 会与 1 构成一对逆序对。此时,[0,1] 还需要贡献 1 对逆序对。
- 末尾元素为 2。前面的两个元素中,任何元素都不能和 2 构成逆序对。此时,[0,1] 还需要贡献 2 对逆序对。
定义函数 dfs(end,cnt),用来计算排列逆序对为 cnt 且满足 requirements 的排列 perm[0…end] 的个数。代入示例 ,我们可以得到 dfs(2,2)=dfs(1,0)+dfs(1,1)+dfs(1,2) 的递推公式。
更一般地,计算dfs(end,cnt),我们可以得到以下递推公式:
- 如果
[0,end−1]在requirements有要求逆序对数量,且对应的逆序对要求数量为r,那么我们在计算dfs(end,cnt)时,因为[0,end-1]的逆序对个数为r,前面的元素需要与最后一个元素贡献cnt−r个逆序对,因为排列的每个元素都不一样,最后一个元素的取值要么不存在,要么唯一确定。这个逆序对的个数满足0≤cnt−r≤end。因此,当满足r≤cnt≤end+r时,dfs(end,cnt)=dfs(end−1,r);否则,dfs(end,cnt)=0。 - 如果
end−1不在requirements有要求。那么我们遍历末尾元素所有的可能性。遍历的范围为0∼min(end,cnt),得到递推公式dfs(end,cnt)=∑ i=0,min(end,cnt) dfs(end−1,cnt−i)。
注意需要对 dfs 应用记忆化搜索,定义数组memo,meno[i][j]存储dfs(i,j)的计算结果,这样每个状态最多被计算一次,降低时间复杂度。
最后返回 dfs(n−1,reqMap[n−1])即可,其中 reqMap 是将 requirements 转化成的键值对,键为 endi,值为 cnti。
代码
int numberOfPermutations(int n, vector<vector<int>>& requirements) {const int MOD = 1e9+7;vector<int> req(n, -1);req[0] = 0;for (auto& p : requirements) {req[p[0]] = p[1];}if (req[0]) {return 0;}int m = ranges::max(req);vector<vector<int>> memo(n, vector<int>(m + 1, -1)); // -1 表示没有计算过auto dfs = [&](auto&& dfs, int i, int j) -> int {if (i == 0) {return 1; //i为0,直接返回1}int& res = memo[i][j]; // 注意这里是引用if (res != -1) { // 之前计算过return res;}res = 0;if (int r = req[i - 1]; r >= 0) { //r大于0,说明在req中有逆序对数量要求if (j >= r && j <= r + i) { //对于满足要求的j,res值唯一确定,继承前者dfs(i-1,r)。res = dfs(dfs, i - 1, r);}} else {for (int k = 0; k <= min(i, j); k++) { //前面元素和当前最后一位组成k对逆序对,最多不会超过i。res = (res + dfs(dfs, i - 1, j - k)) % MOD; //对于每个枚举的k,前面元素需组成j - k对逆序对}}return res;};return dfs(dfs, n - 1, req[n - 1]);}
剪枝技巧
组合总数
问题描述
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
原题链接
代码
vector<vector<int>>tar;vector<int>tr;int s;void dfs(vector<int>& c,int begin,int t){if(t==0) {tar.push_back(tr);return;}/*在搜索中去重,每一次搜索的时候设置 下一轮搜索的起点 begin从每一层的第 2 个结点开始,都不能再搜索产生同一层结点已经使用过的 candidate 里的元素。*/for(int i=begin;i<s&&t-c[i]>=0;i++){ //t-c[i]>=0,减枝tr.push_back(c[i]);dfs(c,i,t-c[i]); tr.pop_back(); //回朔}}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {s=candidates.size();if(s==0) return tar;sort(candidates.begin(),candidates.end()); //排序是剪枝的前提dfs(candidates,0,target);return tar;}
买瓜
蓝桥杯2023年省赛题
问题描述
小蓝在瓜摊上买瓜。瓜摊上共有n个瓜,每个瓜的重量为Ai,小蓝可以把任何瓜劈成完全等重的两份,不过每个瓜最多劈一刀。小蓝希望买的瓜的重量之和为m。输出小蓝至少要劈多少个瓜才能买到总重量恰好为m的瓜,如果无论如何都无法得到总重量恰好为m的瓜,则输出-1。
原题链接
思路分析
每个西瓜可以有1.选整个,2.不选,3.选一半 三种选择,枚举所有总重量等于m的组合方案,选出劈瓜数最少得那个。如果纯暴力的话,总复杂度将达到O(3^n).
可通过剪枝来优化一下时间复杂度:
- 选取的瓜的总重量已经大于等于m,可以不用继续【递】下去,直接【归】。
- 维护一个最小劈瓜数ans,当前劈瓜数已经大于等于ans时不用再【递】下去,直接【归】。
- 定义一个后缀数组sum,记录sum[i]记录
[i,n-1]区间内所有西瓜的总重量,当前面选取西瓜重量+后面所有西瓜总重量都不足以等于m时不用再【递】下去,直接【归】。
代码
#include <bits/stdc++.h>
using namespace std;int ans=50;//ans维护最小劈瓜数 先设为一个大值int a[50];//存瓜 原数组int sum[50];//表示的是从第 i 个瓜到第 n 个瓜的总质量int n,m;void dfs(int S,int i,int cnt)//总和,下标,劈瓜计数器
{if(cnt>=ans)return;//剪枝if(S==m) ans=min(ans,cnt);//如果相等,说明劈瓜劈够了,返回已经劈了几次瓜if(i>=n||S>=m||S+sum[i]<m) return ;//递归结束条件dfs(S+a[i],i+1,cnt);//买一个瓜dfs(S+a[i]/2,i+1,cnt+1);//买半个瓜,计数器+1dfs(S,i+1,cnt);//不买当前瓜,跳到下一个瓜
}
int main()
{ios::sync_with_stdio(false); cin.tie(0),cout.tie(0); cin>>n>>m;m<<=1;//总质量也要*2才能保证结果不受影响for(int i=0;i<n;i++) cin>>a[i],a[i]<<=1;//为了防止劈瓜出现小数,将其左移一位*2倍//遍历所有的瓜for(int i=n-1;i>=0;i--){sum[i]=sum[i+1]+a[i];//记录后缀数组}dfs(0,0,0);if(ans==50)cout<<-1; //最终 ans 仍然为初始值 50,则表示无法通过劈瓜的方式满足要求else cout<<ans;return 0;
}
相关文章:

017搜索之深度优先DFS——算法备赛
深度优先搜索 如果说广度优先搜索是逐层扩散,那深度优先搜索就是一条道走到黑。 深度优先遍历是用递归实现的,预定一条顺序规则(如上下左右顺序) ,一直往第一个方向搜索直到走到尽头或不满足要求后返回上一个叉路口按…...

解决 maven编译项目-Fatal error compiling: 无效的目标发行版: 21 -> [Help 1]
目录 1. 问题描述 2. 排查思路 3. 设置-指定maven使用jdk21 4. 参考资料 1. 问题描述 在idea中使用maven编译时,在系统环境变量中已经设置了jdk为21,但是在执行mvn package时,确提示 Fatal error compiling: 无效的目标发行版: 21 -> [Help 1] [ERROR] Failed to e…...

Thinkphp6实现websocket
项目需要连接一台自动售货机,售货机要求两边用websocket连接,监听9997端口。本文实现了一个基于PHP的WebSocket服务器,用于连接自动售货机,支持start/stop/restart命令操作 1.新建文件 新建文件 /command/socket.php <?php namespace a…...

web-css
一.CSS选择器: 1.基础选择器 基本选择器: >.标签选择器 格式:标签名称{} >.类选择器(重) 格式:.class属性的值{} >.id选择器 格式:#id属性的值{} >.通配符(表示所有&am…...

关于 smali:2. 从 Java 到 Smali 的映射
一、对照 Java 代码与 Smali 代码差异 1.1 方法调用差异:Java vs Smali Java 方法分类: 方法类型Java 示例Smali 指令特点说明静态方法Utils.print("hi")invoke-static没有 this 指针实例方法obj.show()invoke-virtual有 this,虚…...

三、zookeeper 常用shell命令
作者:IvanCodes 日期:2025年5月28日 专栏:Zookeeper教程 ZooKeeper Shell (zkCli.sh) 是与ZooKeeper服务器交互的核心工具。本教程将详细介绍常用命令,并重点解析ZooKeeper数据节点 (ZNode) 的特性与分类。 思维导图 一、连接 Zo…...

分布式流处理与消息传递——Paxos Stream 算法详解
Java 实现 Paxos Stream 算法详解 一、Paxos Stream 核心设计 #mermaid-svg-cEJcmpaQwLXpEbx9 {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-cEJcmpaQwLXpEbx9 .error-icon{fill:#552222;}#mermaid-svg-cEJcmpaQw…...

智变与重构:AI 赋能基础教育教学的范式转型研究报告
一、研究背景与核心价值 (一)技术驱动下的教育转型浪潮 在全球数字化转型加速的背景下,人工智能作为核心技术力量,正重塑基础教育生态。据《人工智能赋能未来教育研究报告》指出,我国教育数字化战略行动已推动超 70…...

平衡三进制
平衡三进制 - OI Wiki https://oi-wiki.org/math/balanced-ternary/ 上海市计算机学会竞赛平台 | YACS 方法一,先分离后进位 #include <iostream> using namespace std; int n, a[100], cnt; bool flag; int main() {cin >> n;if(n0){cout <<…...
、轻量级工具、在线开发平台、代码管理工具等))
针对Python开发的工具推荐及分析,涵盖集成开发环境(IDE)、轻量级工具、在线开发平台、代码管理工具等)
以下是针对Python开发的工具推荐及全面分析,涵盖集成开发环境(IDE)、轻量级工具、在线开发平台、代码管理工具等,结合不同场景和需求进行分类说明: 目录 一、集成开发环境(IDE) 1. PyCharm 2…...

960g轻薄本,把科技塞进巧克力盒子
朋友们,谁懂啊 最近本打工人被同事疯狂种草了一款 “巧克力盒子” 华硕灵耀 14 Air 骁龙版! 960g的重量比一瓶大可乐还轻 塞进通勤包毫无压力 连健身房的瑜伽垫都能多卷两圈 这台行走的生产力工具,到底有啥魔法? 今天就带…...

xcode 编译运行错误 Sandbox: rsync(29343) deny(1) file-write-create
解决方法 方法一:修改Targets -> Build Settings 中 ENABLE_USER_SCRIPT_SANDBOXING 设置 NO 方法二:项目使用cocoaPods进行三方管理 且 使用了 use_frameworks,把 use_frameworks 注释掉,然后重新自行pod install...

C# 基于 Windows 系统与 Visual Studio 2017 的 Messenger 消息传递机制详解:发布-订阅模式实现
🧑 博主简介:CSDN博客专家、CSDN平台优质创作者,高级开发工程师,数学专业,10年以上C/C, C#, Java等多种编程语言开发经验,拥有高级工程师证书;擅长C/C、C#等开发语言,熟悉Java常用开…...

ComfyUI+阿里Wan2.1+内网穿透技术:本地AI视频生成系统搭建实战
文章目录 前言1.软件准备1.1 ComfyUI1.2 文本编码器1.3 VAE1.4 视频生成模型 2.整合配置3. 本地运行测试4. 公网使用Wan2.1模型生成视频4.1 创建远程连接公网地址 5. 固定远程访问公网地址总结 前言 各位技术爱好者,今天为您带来一组创新性的AI应用方案!…...

腾讯云开发者社区文章内容提取免费API接口教程
接口简介: 提取指定腾讯云开发者社区文章内容。本接口仅做内容提取,未经作者授权请勿转载。 请求地址: https://cn.apihz.cn/api/caiji/tencent.php 请求方式: POST或GET。 请求参数: 【名称】【参数】【必填】【说…...

利用海外代理IP,做Twitter2026年全球趋势数据分析
近年来,社交媒体趋势分析逐渐成为品牌监控、市场洞察和消费者研究的必备工具。而当谈到全球趋势数据分析,很多人都会立即想到 Twitter趋势(逼近连美丽国的总统都喜欢在上面发表自己的看法- -!!!)。Twitter趋势,即Twitt…...

OpenLayers 图形交互编辑
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 图形要素包括属性信息和几何信息,在实际应用中,不仅需要修改样式信息,也需要修改图形几何信息。在OpenLayers中&…...

pikachu靶场通关笔记06 XSS关卡02-反射型POST
目录 一、XSS 二、反射型XSS 三、POST型报文 四、GET型与POST型区别 五、代码审计 五、渗透实战 1、渗透方法1 2、渗透方法2 本系列为通过《pikachu靶场通关笔记》的XSS关卡(共10关)渗透集合,通过对XSS关卡源码的代码审计找到XSS风险的真实原因&…...
SQLiteStudio - 免费开源、轻量高效,跨平台的 SQLite 数据库管理工具,代替 Navicat for SQLite
管理 SQLite 数据库就用这款软件,真的早该摒弃破解和盗版的 Navicat 了。 SQLiteStudio 是一款专注于管理 SQLite 数据库 的桌面软件,用于浏览和编辑 SQLite 数据库文件。软件的作者是来自波兰的开发者 Paweł Salawa,他是一位拥有 20 年 Ja…...

Prometheus + Grafana + Cadvisor:构建高效企业级服务监控体系
在现代软件开发和运维领域,容器化技术的应用越来越广泛,其中 Docker 作为最受欢迎的容器化解决方案之一,其容器的监控管理变得至关重要。本文将详细介绍如何使用 cadvisor、Prometheus 和 Grafana 来监控 Docker 容器的状态。 一、安装镜像 …...

WEBSTORM前端 —— 第3章:移动 Web —— 第2节:空间转换、转化
目录 一、空间转换 1.空间转换 2.空间转换 – 平移 3.视距 perspective 4.空间 – 旋转 ③空间旋转——Z轴代码与效果视频 ④空间旋转——X轴代码与效果视频 ⑤空间旋转——Y轴代码与效果视频 5.立体呈现 – transform-style 案例 – 3D 导航 6.空间转换 – 缩放 …...

Java研学-MongoDB(一)
一 MongoDB 简介 MongoDB是一种高性能、开源的NoSQL数据库,采用面向文档的存储模型,以BSON(Binary JSON)格式存储数据,具有灵活的数据模型、强大的扩展性和丰富的功能特性,广泛应用于各类现代应用程序的数据…...

【AI面试秘籍】| 第25期:RAG的关键痛点及解决方案深度解析
今天我们来聊聊大模型领域一个非常火热的技术——RAG(Retrieval Augmented Generation)。RAG通过引入外部知识库,有效地缓解了大型语言模型(LLM)在处理知识密集型任务时可能出现的幻觉、知识过时等问题。然而ÿ…...

OpenGL、GLUT、freeGLUT 与 GLFW 的区别
在图形编程中,OpenGL 是最核心的渲染 API,但仅靠它本身无法完成窗口创建、事件处理等任务。因此,开发者通常会借助一些辅助库来简化开发流程。常见的库包括 GLUT、freeGLUT 和 GLFW。 本文将详细讲解这些技术之间的区别,并提供每…...

服务器带宽线路的区别(GIA、CN2、BGP、CMI等)
服务器带宽线路的区别(GIA、CN2、BGP、CMI等) 一、BGP线路 1. 定义与技术特点 BGP(Border Gateway Protocol,边界网关协议)是一种用于不同自治系统(AS)之间交换路由信息的协议,属…...

ppt一键制作:ai自动生成PPT,便捷高效超级精美!
深夜的台灯下,你对着杂乱的 PPT 内容反复刷新灵感,鼠标在字体、配色选项间来回穿梭,好不容易拼凑出的页面,却总透着浓浓的 “廉价感”;汇报在即,逻辑混乱的大纲改了又改,每一页感觉合适又不搭&a…...

多方法解决MNIST数字识别
全连接层 import torch from torchvision import datasets, transforms import torch.nn as nn import torch.optim as optim from tqdm import tqdm # 用于进度条显示 import os# 定义数据预处理(标准化+Tensor转换) transform = transforms.Compose([transforms.ToTensor…...

Maven(黑马)
Maven 是一个强大的项目管理和构建自动化工具,主要用于 Java 项目的构建、依赖管理和文档生成。它通过使用 POM(Project Object Model)文件来管理项目的配置和依赖关系,从而实现项目的自动化构建和管理。以下是 Maven 的一些核心概…...

CppCon 2014 学习:ODB, Advanced Weapons and Tactics
#Schema Evolution 是数据库持久化技术中的一个重要概念,特别是在使用像 ODB 这样的 C ORM 框架时。 展示的代码片段正是 ODB 支持的**模式演化(Schema Evolution)**语法示例。 什么是 Schema Evolution? Schema Evolution 指的…...
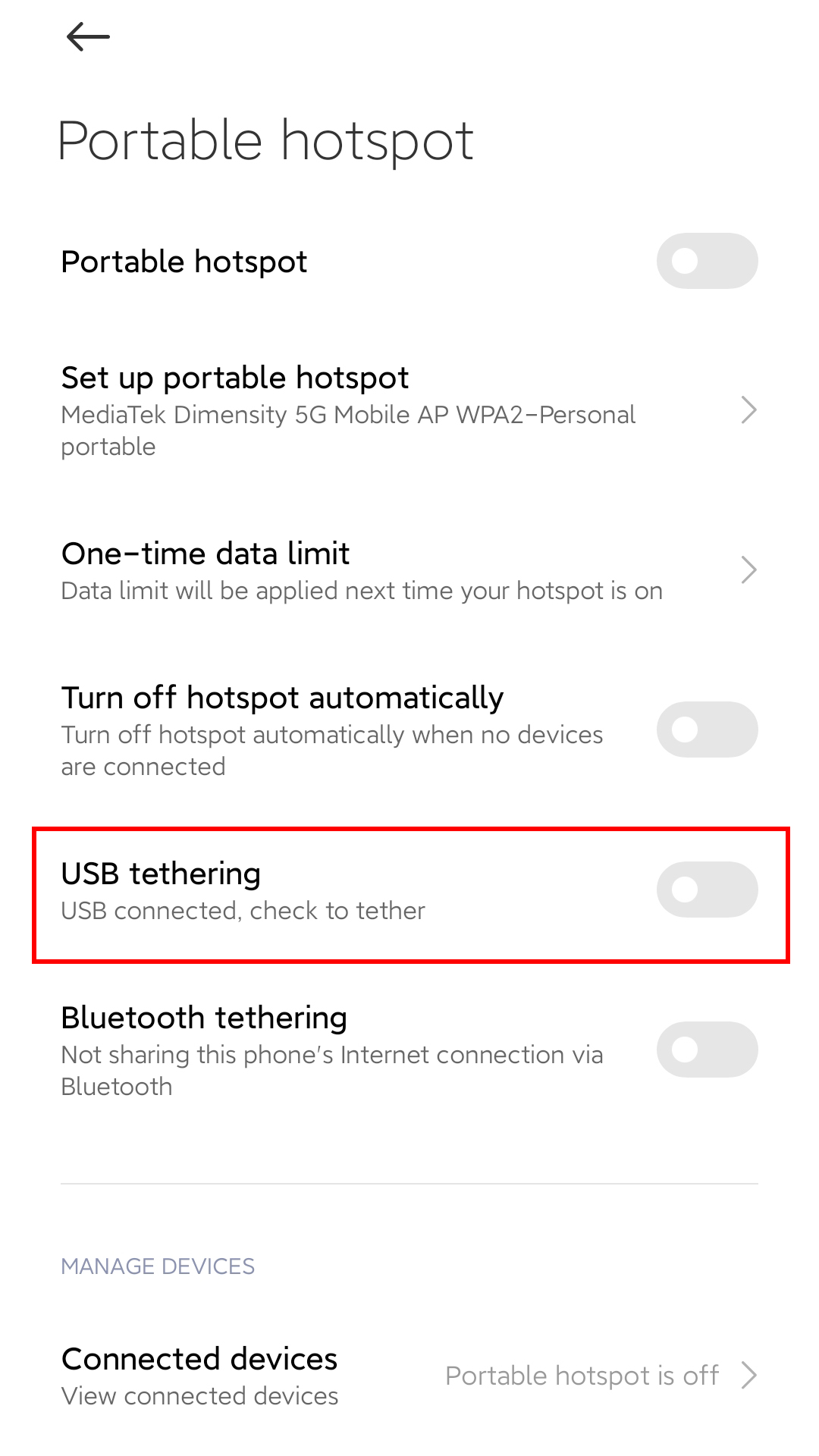
将手机网络经USB数据线和本地局域网共享给华为AP6050DN无线接入点
引言 由于最近装毕的新家所在的小区未能及时通宽带,于是家中各类无线设备如何上网就成了首要要解决的问题。 鉴于家中要联网的设备多、类型杂、支持频段也不一,总是开手机热点不是回事儿,于是就想着把手机网络引至华为AP6050DN无线接入点中,让家中所有的无线设备都能快速高…...
