机器人学基础——正运动学(理论推导及c++实现）

机器人正运动学

机器人正运动学一般是指从机器人的关节位置到基于参考坐标系下末端执行器的位置。

平移变换和旋转变换

平移变换

假设我们有两个坐标系A和B，坐标系A与B的方位相同，xyz轴的指向都是一致的，即没有旋转变换。有一点p，则在A坐标系下从A坐标原点到p的位置矢量即为在B坐标系下p的位置矢量加上在A坐标系下B原点的位置矢量，公式如下

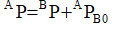
旋转变换

类似上述平移变换，我们假设坐标系A与坐标系B没有平移变换及原点位置一致，只有方位上的变换。如下

这个坐标系A和坐标系B原点一致并且在方位上不同，可以看成将坐标系A经过某个旋转变换进程为了B坐标系的方位。我们将这个变换的过程记为
上标为参考坐标系，这个变换也可以解释为B坐标系在A坐标系下的方位

复合变换

当两个坐标系之间的关系坐标原点没有重合方位也不是一致的时候我们该怎么描述这个变换过程呢？
当坐标系A与B无法使用单独的平移变换或者单独的旋转变换来描述时，我们可以将这个过程看作是先经过平移后经过旋转或者先经过旋转再经过平移来描述。由于这个过程都是的参考系都是A坐标系即参考坐标系是固定的，所以先平移还是先旋转是没有区别的。

假设有一点p,在A坐标系下位置是，在B坐标系下的描述为，从坐标系A到B的旋转变换为，坐标系A到B的平移变换为

A到B的平移变换即为平移变换部分讲的在A坐标系下B的坐标原点的矢量。那么具有下面这个关系

数学描述

对平移变换和旋转的概念大致有了一个了解，那么具体应该应该怎么计算呢？不管是平移变换还是旋转变换我们都可以使用矩阵来描述这个过程。

平移矩阵

我们知道在三维空间中描述点或者矢量可以用x,y,z三个量来表达和描述。
而平移变换的本质上即为从坐标系A（参考坐标系）原点到坐标系B（目标坐标系）原点的一个矢量，所以平移矩阵的数学表达可以这样表示

[x,y,z],即为在A坐标系下B坐标系原点的位置

旋转矩阵

坐标系经过旋转变换之后，相对应的点的位置描述也要被改变，那么要怎么使用数学语言来描述这个变换呢
我们可以将从坐标系A到坐标系B的旋转变换分解为绕A（参考坐标系）系的X轴旋转α°，绕Y轴旋转β°，转z轴旋转γ°，三种基本的旋转，其他都可以看作是这三种基础旋转的叠加旋转。
使用矩阵来表示这三种旋转方式
绕x转α°：

绕y轴旋转：

绕z轴旋转

c++实现

根据以上基础理论我们大致了解了机器人正运动学中基础的旋转变换和平移变换，接下来我们就可以使用这些来进行机器人正解我们使用c++来完成这个过程，假设我们有一个urdf模型，那么第一步我们需要对这个模型进行解析

导入解析urdf模型

打开一个终端，进入之前下载的frank机械臂的工作空间内，我们新创建一个功能包frank_fk，用来表示正运动学求解的功能包

~/franka/src/franka_ros$ catkin_create_pkg franka_fk  rospy roscpp std_msgs

我们新建一个cpp

~/franka/src/franka_ros/franka_fk/src$ touch frank_fk.cpp
~/franka/src/franka_ros/franka_fk/include/franka_fk$ touch frank_fk.h

在panda机器人里面使用的是.urdf.xacore文件，我们需要对这个文件进行预处理变成urdf格式的文件才可以使用c++的接口对其进行读取解析
使用终端命令行将这个.urdf.xacore转换成urdf格式的文件

cd franka/
source ./devel/setup.bash 
rosrun xacro xacro src/franka_ros/franka_description/robots/panda/panda.urdf.xacro > panda.urdf

可以看到在franka下生成了一个panda.urdf文件，我们将它移动到panda.urdf.xacore路径下

使用vscode打开刚才创建的frank_fk
键入以下代码

franka_fk.h
#include <eigen3/Eigen/Dense>
#include <urdf/model.h>
#include <string>
#include <fstream>
#include <sstream>
#include <stdexcept>
#include <cstdlib>
#include <map>class ROBOTFK
{
public:int Readmodel(std::string modelpath);Eigen::Matrix4d GetEndPos(std::map<std::string,double> jointname);
private:Eigen::Matrix3d GetJointpos();urdf::Model pdmodel;};

franka_fk.cpp
#include <iostream>
#include <urdf_model/model.h>
#include <frank_fk.h>
#include <ros/ros.h>
int ROBOTFK::Readmodel(const std::string modelpath)
{int a = pdmodel.initFile(modelpath);std::cout << "Robot Name: " << pdmodel.getName() << std::endl;return a;
}
bool fileExists(const std::string& path) {std::ifstream file(path);return file.good();
}
int main()
{ROBOTFK robotfk;int success = robotfk.Readmodel("src/franka_ros/franka_description/robots/panda/panda.urdf");return 0;
}

cmakelistcmake_minimum_required(VERSION 3.0.2)
project(franka_fk)#add_compile_options(-std=c++11)
find_package(catkin REQUIRED COMPONENTSroscpprospyurdfstd_msgs
)catkin_package(INCLUDE_DIRS include/franka_fk
)include_directories(include/franka_fk${catkin_INCLUDE_DIRS}
)${catkin_EXPORTED_TARGETS})add_executable(main src/frank_fk.cpp)target_link_libraries(main${catkin_LIBRARIES}
)

可以使用这个cpp暂时来进行urdf模型文件的读取，查看是否可以读取到正确的文件，接下来来进行一个简单的编译和运行

catkin_make
source ./devel/setup.bash
rosrun franka_fk main

可以看到运行结果是这样的

Robot Name: panda

这说明已经检测到正确的urdf文件并且读取出来我们的机器人名称为：panda

单关节旋转矩阵的计算

接下来我们对机器人单关节的变换矩阵进行c++的实现，需要从urdf模型中获取到我门制定关节对应的旋转轴（旋转类型）和相对上一关节位置的位移量，所以我们对Eigen::Matrix3d GetJointpos();这个函数进行填充

---

后面会补充…