行列式详解:从定义到应用
行列式详解:从定义到应用
引言
行列式是线性代数中的核心概念之一,它不仅是矩阵理论的重要组成部分,更是解决线性方程组、计算向量空间体积、判断矩阵可逆性等问题的关键工具。本文将从行列式的基本定义出发,系统地介绍其性质、计算方法和重要应用。
思维导图
mindmaproot((行列式))定义二阶行列式三阶行列式n阶行列式余子式和代数余子式性质转置不变性行列交换变号线性性质乘积性质计算方法按行列展开化上三角矩阵利用性质简化特殊行列式范德蒙德行列式对角行列式上下三角行列式应用克拉默法则矩阵可逆性判断体积计算线性相关性判断
1. 行列式的定义
1.1 二阶行列式
最简单的行列式是二阶行列式,定义为:
∣ a 11 a 12 a 21 a 22 ∣ = a 11 a 22 − a 12 a 21 \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix} = a_{11}a_{22} - a_{12}a_{21} a11a21a12a22 =a11a22−a12a21
这个公式可以理解为主对角线元素乘积减去副对角线元素乘积。
例如:
∣ 3 2 1 4 ∣ = 3 × 4 − 2 × 1 = 12 − 2 = 10 \begin{vmatrix} 3 & 2 \\ 1 & 4 \end{vmatrix} = 3 \times 4 - 2 \times 1 = 12 - 2 = 10 3124 =3×4−2×1=12−2=10
1.2 三阶行列式
三阶行列式的计算可以使用萨吕斯(Sarrus)法则或按行(列)展开:
∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ = a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 − a 13 a 22 a 31 − a 11 a 23 a 32 − a 12 a 21 a 33 \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix} = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} - a_{13}a_{22}a_{31} - a_{11}a_{23}a_{32} - a_{12}a_{21}a_{33} a11a21a31a12a22a32a13a23a33 =a11a22a33+a12a23a31+a13a21a32−a13a22a31−a11a23a32−a12a21a33
1.3 余子式和代数余子式
对于n阶行列式中的元素 a i j a_{ij} aij:
- 余子式 M i j M_{ij} Mij:去掉第i行第j列后得到的 ( n − 1 ) (n-1) (n−1)阶行列式
- 代数余子式 A i j A_{ij} Aij: A i j = ( − 1 ) i + j M i j A_{ij} = (-1)^{i+j}M_{ij} Aij=(−1)i+jMij
1.4 n阶行列式的定义
n阶行列式可以按第i行展开定义为:
∣ A ∣ = ∑ j = 1 n a i j A i j |A| = \sum_{j=1}^n a_{ij}A_{ij} ∣A∣=j=1∑naijAij
或按第j列展开定义为:
∣ A ∣ = ∑ i = 1 n a i j A i j |A| = \sum_{i=1}^n a_{ij}A_{ij} ∣A∣=i=1∑naijAij
2. 行列式的重要性质
2.1 基本性质
- 转置不变性: ∣ A T ∣ = ∣ A ∣ |A^T| = |A| ∣AT∣=∣A∣
- 行列交换变号:交换两行(列),行列式变号
- 比例性:某一行(列)乘以k,行列式也乘以k
- 加法性:某一行(列)是两个向量之和,行列式等于两个行列式之和
2.2 重要推论
- 有零行(列)的行列式等于0
- 有两行(列)相同的行列式等于0
- 有两行(列)成比例的行列式等于0
- 某一行(列)的k倍加到另一行(列),行列式不变
2.3 乘积性质
∣ A B ∣ = ∣ A ∣ ∣ B ∣ |AB| = |A||B| ∣AB∣=∣A∣∣B∣
这是行列式最重要的性质之一,对于理解矩阵的几何意义具有重要作用。
3. 行列式的计算方法
3.1 按行(列)展开法
这是定义性的计算方法,适用于任意阶数的行列式:
∣ A ∣ = ∑ j = 1 n a i j A i j (按第i行展开) |A| = \sum_{j=1}^n a_{ij}A_{ij} \quad \text{(按第i行展开)} ∣A∣=j=1∑naijAij(按第i行展开)
计算技巧:选择零元素最多的行或列进行展开,可以大大简化计算。
3.2 化上三角矩阵法
利用行列式性质,通过行变换将矩阵化为上三角形式,此时行列式等于对角元素的乘积。
步骤:
- 用行变换将矩阵化为上三角形
- 记录行变换对行列式的影响
- 计算对角元素乘积
例子:
∣ 2 1 3 4 2 1 1 3 2 ∣ \begin{vmatrix} 2 & 1 & 3 \\ 4 & 2 & 1 \\ 1 & 3 & 2 \end{vmatrix} 241123312
通过行变换:
∣ 2 1 3 0 0 − 5 0 5 2 1 2 ∣ \begin{vmatrix} 2 & 1 & 3 \\ 0 & 0 & -5 \\ 0 & \frac{5}{2} & \frac{1}{2} \end{vmatrix} 20010253−521
交换第二、三行(变号):
− ∣ 2 1 3 0 5 2 1 2 0 0 − 5 ∣ = − 2 × 5 2 × ( − 5 ) = 25 -\begin{vmatrix} 2 & 1 & 3 \\ 0 & \frac{5}{2} & \frac{1}{2} \\ 0 & 0 & -5 \end{vmatrix} = -2 \times \frac{5}{2} \times (-5) = 25 − 2001250321−5 =−2×25×(−5)=25
3.3 特殊行列式的计算
对角行列式
∣ a 1 0 ⋯ 0 0 a 2 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ a n ∣ = a 1 a 2 ⋯ a n \begin{vmatrix} a_1 & 0 & \cdots & 0 \\ 0 & a_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & a_n \end{vmatrix} = a_1a_2\cdots a_n a10⋮00a2⋮0⋯⋯⋱⋯00⋮an =a1a2⋯an
范德蒙德行列式
∣ 1 1 ⋯ 1 x 1 x 2 ⋯ x n x 1 2 x 2 2 ⋯ x n 2 ⋮ ⋮ ⋱ ⋮ x 1 n − 1 x 2 n − 1 ⋯ x n n − 1 ∣ = ∏ 1 ≤ i < j ≤ n ( x j − x i ) \begin{vmatrix} 1 & 1 & \cdots & 1 \\ x_1 & x_2 & \cdots & x_n \\ x_1^2 & x_2^2 & \cdots & x_n^2 \\ \vdots & \vdots & \ddots & \vdots \\ x_1^{n-1} & x_2^{n-1} & \cdots & x_n^{n-1} \end{vmatrix} = \prod_{1 \leq i < j \leq n}(x_j - x_i) 1x1x12⋮x1n−11x2x22⋮x2n−1⋯⋯⋯⋱⋯1xnxn2⋮xnn−1 =1≤i<j≤n∏(xj−xi)
4. 行列式的重要应用
4.1 克拉默法则
对于n元线性方程组 A x = b Ax = b Ax=b,当系数矩阵A的行列式 ∣ A ∣ ≠ 0 |A| \neq 0 ∣A∣=0时,方程组有唯一解:
x i = ∣ A i ∣ ∣ A ∣ x_i = \frac{|A_i|}{|A|} xi=∣A∣∣Ai∣
其中 A i A_i Ai是将A的第i列替换为常数列b得到的矩阵。
例子:解方程组
{ 2 x + y = 5 x + 3 y = 8 \begin{cases} 2x + y = 5 \\ x + 3y = 8 \end{cases} {2x+y=5x+3y=8
系数矩阵: A = ( 2 1 1 3 ) A = \begin{pmatrix} 2 & 1 \\ 1 & 3 \end{pmatrix} A=(2113), ∣ A ∣ = 6 − 1 = 5 |A| = 6 - 1 = 5 ∣A∣=6−1=5
x = ∣ 5 1 8 3 ∣ 5 = 15 − 8 5 = 7 5 x = \frac{\begin{vmatrix} 5 & 1 \\ 8 & 3 \end{vmatrix}}{5} = \frac{15 - 8}{5} = \frac{7}{5} x=5 5813 =515−8=57
y = ∣ 2 5 1 8 ∣ 5 = 16 − 5 5 = 11 5 y = \frac{\begin{vmatrix} 2 & 5 \\ 1 & 8 \end{vmatrix}}{5} = \frac{16 - 5}{5} = \frac{11}{5} y=5 2158 =516−5=511
4.2 矩阵可逆性判断
方阵A可逆的充要条件是 ∣ A ∣ ≠ 0 |A| \neq 0 ∣A∣=0。这为判断矩阵是否可逆提供了简便方法。
4.3 几何意义
在几何上,行列式具有重要的体积意义:
- 二阶行列式表示平行四边形的面积
- 三阶行列式表示平行六面体的体积
- n阶行列式表示n维空间中超平行体的"体积"
4.4 线性相关性判断
向量组 { α 1 , α 2 , … , α n } \{\alpha_1, \alpha_2, \ldots, \alpha_n\} {α1,α2,…,αn}线性相关的充要条件是以这些向量为列的矩阵的行列式等于0。
5. 学习建议和常见误区
5.1 学习建议
- 掌握基本计算:熟练掌握2阶、3阶行列式的计算
- 理解几何意义:将行列式与面积、体积联系起来理解
- 多练习性质应用:利用性质简化计算,避免机械展开
- 注意符号:行列式计算中符号错误是常见问题
5.2 常见误区
- 混淆矩阵和行列式:矩阵是数表,行列式是数值
- 忽视行列式性质:不利用性质直接展开,计算复杂
- 符号错误:在按行列展开时符号计算错误
- 几何意义理解不深:仅停留在计算层面,不理解几何背景
结语
行列式作为线性代数的基础概念,不仅具有重要的理论价值,更在实际应用中发挥着关键作用。从简单的二阶行列式到复杂的n阶行列式,从代数计算到几何意义,行列式为我们提供了理解线性关系的强有力工具。
掌握行列式的关键在于:
- 理解其定义和几何意义
- 熟练运用各种计算方法
- 灵活应用行列式性质
- 在实际问题中正确运用
随着学习的深入,你会发现行列式不仅是计算工具,更是理解线性代数美妙结构的窗口。它连接着代数与几何,抽象与具体,为进一步学习特征值、线性变换等高级概念奠定了坚实基础。
相关文章:

行列式详解:从定义到应用
行列式详解:从定义到应用 引言 行列式是线性代数中的核心概念之一,它不仅是矩阵理论的重要组成部分,更是解决线性方程组、计算向量空间体积、判断矩阵可逆性等问题的关键工具。本文将从行列式的基本定义出发,系统地介绍其性质、…...
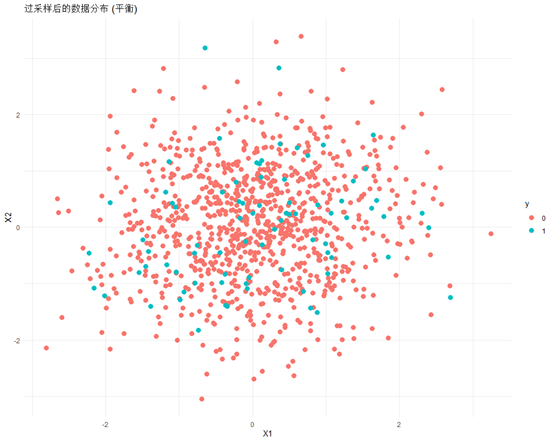
R语言使用随机过采样(Random Oversampling)平衡数据集
随机过采样(Random Oversampling)是一种用于平衡数据集的技术,常用于机器学习中处理类别不平衡问题。当某个类别的样本数量远少于其他类别时(例如二分类中的正负样本比例悬殊),模型可能会偏向多数类&#x…...

HertzBeat的安装和使用教程
以下是HertzBeat的安装和使用教程: 安装 • Docker安装:执行命令docker run -d -p 1157:1157 -p 1158:1158 --name hertzbeat apache/hertzbeat。启动后,访问http://localhost:1157,默认账号密码是admin/hertzbeat。 • 包安装…...

【Kotlin】高阶函数Lambda内联函数
【Kotlin】简介&变量&类&接口 【Kotlin】数字&字符串&数组&集合 【Kotlin】高阶函数&Lambda&内联函数 【Kotlin】表达式&关键字 文章目录 函数还是属性高阶函数抽象和高阶函数实例: 函数作为参数的需求方法引用表达式更多使用场…...

从0开始学vue:vue3和vue2的关系
一、版本演进关系1. 继承关系2. 版本生命周期 二、核心差异对比三、关键演进方向1. Composition API2. 性能优化 四、迁移策略1. 兼容构建模式2. 关键破坏性变更 五、生态演进1. 官方库升级2. 构建工具链 六、选型建议1. 新项目2. 现有项目 七、未来展望 一、版本演进关系 1. …...

MySQL关系型数据库学习
学习参考链接:https://www.runoob.com/mysql/mysql-tutorial.html Windows 安装MYSQL服务端的步骤:https://www.runoob.com/w3cnote/windows10-mysql-installer.html 1. 概念学习 MySQL 是一种关联数据库管理系统,关联数据库将数据保存在不…...

嵌入式硬件篇---龙芯2k1000串口
针对串口错误 “device reports readiness to read but returned no data (Device disconnected or multiple access on port?)” 的排查和解决方法 硬件方面 检查连接 确认串口设备(如串口线、连接的模块等)与龙芯设备之间的物理连接是否牢固…...

4-C#的不同窗口传值
C#的不同窗口传值 1.通过构造函数传值 this.Hide(); Form1 form01 new Form1(textBox2.Text); //Application.Run(form01); form01.Show();public Form1(string aaa) {InitializeComponent();label12.Text aaa; }2.全局类传值 namespace WindowsFormsApp1 {public class G…...
谷歌地图苹果版v6.138.2 - 前端工具导航
谷歌地图(Google maps)苹果版是是由谷歌官方推出的一款手机地图应用。软件功能强大,支持本地搜索查找世界各地的地址、地点和商家;支持在街景视图中查看世界各地的360度全景图;支持查找乘坐火车、公交车和地铁的路线,或者查找步行…...

NSSCTF [LitCTF 2025]test_your_nc
[复现]绕过学的还是太差了,多积累吧 题目 题目: 给了一个python文件 #!/bin/python3 import osprint("input your command")blacklist [cat,ls, ,cd,echo,<,${IFS},sh,\\]while True:command input()for i in blacklist:if i in com…...

第十九章 正则表达式
第十九章 正则表达式 文本型数据在所有的类UNIX系统(如 Linux)中会扮演着重要角色,在完全领会这些工具的全部特征之前,要先了解一下工具最为复杂的用法和相关技术:正则表达式。 什么是正则表达式 简单地说,正则表达式是一种用于…...

browser-use Agent 日志链路分析
browser-use Agent 日志链路分析 本节详细梳理 browser-use Agent 的日志输出,从 Agent 初始化到每一步的行为日志,帮助理解其行为轨迹。 1. Agent 初始化阶段 日志点: logger.info(🧠 Starting a browser-use agent ...) 记录 …...

Qwen3高效微调
高效微调 场景、模型、数据、算力 高效微调的应用场景 对话风格微调:高效微调可以用于根据特定需求调整模型的对话风格。例如,针对客服系统、虚拟助理等场景,模型可以通过微调来适应不同的 语气、礼貌程度 或 回答方式,从而在与…...

Gitee Wiki:重塑关键领域软件研发的知识管理范式
在数字化转型浪潮席卷全球的当下,关键领域软件研发正面临前所未有的知识管理挑战。传统文档管理模式的局限性日益凸显,知识传承的断层问题愈发严重,团队协作效率的瓶颈亟待突破。Gitee Wiki作为新一代知识管理平台,正在通过技术创…...

redis的哨兵模式和Redis cluster
目录 一. redis的主从复制 二. 哨兵模式 2.1 定义 2.2 作用 2.3 配置实例 三. Redis cluster 3.1 定义 3.2 作用 3.3 配置实例 1. 新建集群文件目录 2. 准备可执行文件到每个文件夹 3. 开启群集功能 4. 启动redis节点 5. 查看是否启动成功 6. 启动集群 7. 测试…...

MySQL计算精度计算加减乘除取模方式和方法总计
以下是 MySQL 中常用计算方式和方法 的总结,涵盖不同场景下的使用方式及示例说明: 1. 基本算术运算 适用场景: 对表中的字段或数值进行基础数学运算(加、减、乘、除、取模)。适用于单条记录的字段计算(如单价+税金、折扣后的价格等)。运算符: 运算符描述示例+加法SELE…...

农业机器人的开发
农业机器人的开发 喷农药机器人 番茄采摘机器人 葡萄采摘机器人 黄瓜采摘机器人 西瓜采摘机器人 蘑菇采摘机器人 草莓采摘机器人 草莓采摘机器人综述 视觉系统 CCD摄像机,距离传感器,PC计算机 其中CCD摄像机的作用是进行彩色图像的采集和进行果…...

Swift 解锁 LeetCode 热门难题:不改数组也能找出重复数字?
文章目录 摘要描述题解答案题解代码分析解读: 示例测试及结果时间复杂度空间复杂度总结实际场景类比可运行 Demo(Swift Playground)未来展望 摘要 在数组中找出唯一的重复数字,听起来像一道简单的题目,但如果你不能修…...

2025年微信小程序开发:趋势、最佳实践与AI整合
引言 微信小程序自2017年推出以来,已成为中国互联网生态中不可或缺的一部分。根据最新数据,截至2024年,微信小程序的日活跃用户超过4.5亿,总数超过430万个,95%的中国企业拥有自己的小程序(WeChat Mini Pro…...

【深度学习】15. Segment Anything Model (SAM) :基于提示的分割新时代
Segment Anything Model (SAM) :基于提示的分割新时代 基本介绍 The first foundation model for promptable segmentation. Segment Anything Model(简称 SAM)是 Meta AI 于 2023 年提出的一种通用型图像分割基础模型。与以往分割模型不同&…...

Java从入门到精通 - 常用API(一)
常用 API 此笔记参考黑马教程,仅学习使用,如有侵权,联系必删 文章目录 常用 API1. 包代码演示 2. String2.1 String 概述代码演示总结 2.2 String 的常用方法代码演示 2.3 String 使用时的注意事项第一点第二点代码演示 总结题目 2.4 String…...

SQL 筛选出在表1但不在表2中的数据
SQL 筛选出在表1但不在表2中的数据 在SQL中,要筛选出存在于表1但不存在于表2中的数据,有几种常见的方法: 方法1:使用LEFT JOIN WHERE IS NULL SELECT t1.* FROM table1 t1 LEFT JOIN table2 t2 ON t1.join_key t2.join_key W…...

MATLAB实战:实现数字调制解调仿真
以下是使用MATLAB实现BPSK和QPSK数字调制解调仿真的完整代码。该代码包括调制、AWGN信道、匹配滤波/相关解调、星座图绘制以及误码率计算与理论值比较。 %% 清理环境 clear all; close all; clc; %% 参数设置 numBits 100000; % 传输比特数 EbN0_dB 0:2:10; …...
-2 输入一个数,统计这个数二进制中1的个数)
ccf中学生计算机程序设计入门篇课后题p164页test(1)-2 输入一个数,统计这个数二进制中1的个数
include <iostream> using namespace std;int main() {int x;int n 0;// 输入数据cin >> x;// 统计x二进制中1的个数for (n 0; x ! 0; x & x - 1) {n;}// 输出结果cout << n << endl;return 0; }程序解释: 输入:程序从标…...

实现Cursor + Pycharm 交互
效果演示: 直接可以在cursor或Pycharm中点击右键点击,然后就可以跳转到另一个应用的对应位置了 使用方法: 分别在两个应用中安装插件【Switch2Cursor Switch2IDEA,这两个插件分别安装在 IDEA 和 Cursor 中】: Switc…...

C++标准模板库
C标准库参考: C 标准库-CSDN博客 标准模板库STL C 标准库 和 STL 的关系 1. 严格来说,STL ≠ C 标准库 STL(Standard Template Library) 是 C 标准库的一个子集,主要提供泛型编程相关的组件(如容器、迭代器…...

dvwa6——Insecure CAPTCHA
captcha:大概是“我不是机器人”的一个勾选框或者图片验证 LOW: 先输入密码正常修改试一下(123),发现报错 查看源码: <?phpif( isset( $_POST[ Change ] ) && ( $_POST[ step ] 1 ) ) {// Hide the C…...

【机器学习及深度学习】机器学习模型的误差:偏差、方差及噪声
机器学习模型的误差分析 V1.0机器学习模型的衡量准则概念引入机器学习模型误差分析误差出现的原因及消除 V1.0 机器学习模型的衡量准则 衡量机器学习模型的好坏可以考虑以下几个方面: 偏差(Bias): 在充分训练的情况下࿰…...

【学习笔记】On the Biology of a Large Language Model
On the Biology of a Large Language Model 1 Introduction 目标是对这些模型的内部工作机制进行逆向工程,从而更好地理解它们,并评估它们是否适合特定用途。 正如细胞是生物系统的基本构建单元,我们假设特征是模型内部计算的基本单位。仅仅…...

飞腾D2000,麒麟系统V10,docker,ubuntu1804,小白入门喂饭级教程
#下载docker Index of linux/static/stable/ 根据电脑的CPU类型选择: Intel和AMD选x86_64飞腾D2000选aarch64 #选择较新的版本 #在包含下载的docker-XX.X.X.tgz的文件夹中右键->打开终端 # 解压安装包(根据实际下载的文件) tar -zxvf …...
