李沐《动手学深度学习》 | 数值稳定性
文章目录
- 数值稳定性
- 梯度消失
- Sigmoid作为激活函数
- 梯度爆炸
- 让训练更加稳定
- 合理的权重初始化
- Xavier初始化(常用)
- He初始化/Kaiming方法
- Batch Normalization
- Q&A
数值稳定性
当神经网络的深度比较深时,非常容易数值不稳定。
不稳定梯度是指神经网络反向传播过程中,梯度出现极端数值的现象。
假设有一个d层的神经网络,每一层的变化定义为 f t f_t ft,该变换的权重参数为 W ( t ) W^{(t)} W(t),将第t-1层的输出 h t − 1 h^{t-1} ht−1作为输入传到第t层 f t f_t ft得到第t层的输出 h t = f t ( h t − 1 ) h^t = f_t(h^{t-1}) ht=ft(ht−1)。
计算损失关于参数 W t W_t Wt的梯度,从第d层反向传播到第t层会进行d-t次的矩阵乘法,会带来两个常见的问题①梯度爆炸 ②梯度消失

梯度消失
梯度消失:参数更新过小,在每次更新时几乎不会移动,导致模型无法学习。
若每层的局部梯度 ∣ ∂ h d ∂ h d − 1 ∣ < 1 ∣\frac{∂h^d}{∂h^{d-1}}∣<1 ∣∂hd−1∂hd∣<1,梯度会指数级衰减。
梯度消失的问题
- 底层参数几乎不更新: Δ w ≈ 0 Δw≈0 Δw≈0
- 训练停滞:损失函数长期不下降,不管如何选择学习了率
- 底层无法学习有效特征,仅顶部层训练较好,无法让神经网络更深。
梯度反向传播从顶部开始往底部传,传到后面梯度越来越小,学习效果越来越差。
Sigmoid作为激活函数
σ ( x ) = 1 1 + e − x , σ ′ ( x ) = σ ( x ) ( 1 − σ ( x ) ) \sigma(x)=\frac{1}{1+e^{-x}},\sigma'(x)=\sigma(x)(1-\sigma(x)) σ(x)=1+e−x1,σ′(x)=σ(x)(1−σ(x))

案例说明
对于第 l l l 层的前向传播流程
- 接收输入: z [ l − 1 ] z^{[l−1]} z[l−1]
- 线性变换: a [ l ] = W [ l ] z [ l − 1 ] + b [ l ] a^{[l]}=W^{[l]}z^{[l−1]}+b^{[l]} a[l]=W[l]z[l−1]+b[l]
- 激活函数: z [ l ] = σ ( a [ l ] ) z^{[l]}=\sigma(a^{[l]}) z[l]=σ(a[l])
现在需要通过反向传播计算 ∂ L ∂ W [ l ] \frac{∂L}{∂W[l]} ∂W[l]∂L


激****活函数可能会梯度消失
即使只是某一层输入接近 0(梯度最大为 0.25),在深层网络中梯度仍需连续相乘:0.25 × 0.25 × ... × 0.25 → 指数衰减趋近于 0。说明只要任意一层的输入在梯度不敏感区,其后所有层的梯度被清零。
要求所有层输入值都精准的落在[-2,2]梯度敏感区间,且初始化必去完美,这在实践中几乎不可能。
这个问题曾经困扰深度网络训练,后来更稳定的ReLU系列函数已经成为从业者的默认选择。
梯度爆炸
梯度爆炸:梯度爆炸是指在深度神经网络的反向传播过程中,梯度值变得异常巨大(通常是指数级增长),导致参数更新幅度过大,破坏模型稳定性的现象。
若每层的局部梯度 ∣ ∂ h d ∂ h d − 1 ∣ > 1 ∣\frac{∂h^d}{∂h^{d-1}}∣>1 ∣∂hd−1∂hd∣>1,梯度会指数级增长。
梯度爆炸的问题
- 发生数值溢出:梯度值超过浮点数表示范围(NaN 值)
- 对学习率敏感 w n e w = w − η ⋅ ∇ w w_{new}=w−η⋅∇w wnew=w−η⋅∇w,其中 ∇ w ∇w ∇w 极大
- 如果学习率太大-> 大参数值->更大的梯度
- 如果学习率太小-> 训练无法进展
- 需要再训练过程不断调整学习率
- 模型震荡发散:损失函数剧烈波动,无法收敛
让训练更加稳定
目标:让梯度值在合理的范围内
常见缓解方法
- 将乘法变为加法 CNN常用ResNet、RNN常用LSTM(之后内容)
- 梯度归一化,梯度裁剪(之后内容)
- 合理的权重初始和激活函数(本章内容)
合理的权重初始化
如果想减少权重的值,初始化就应该将其设为较小值。
神经网络权重常用初始化weights = np.random.randn(样本数, 特征数) * 0.01
生成一个二维数组,包含样本数*特征数个随机数,每个元素都是从标准正态分布 N ( 0 , 1 ) N(0,1) N(0,1) 中独立抽取的样本。最后为了避免初始值过大导致梯度爆炸,将每个元素值缩小100倍。
问题:可以将权重初始化设置为0吗?
解答:不希望将权重初始化为相同的值,在反向传播中,所有的权重都会进行相同的更新。相当于只有一个神经元在工作。为了防止权重均一化,必须随机生成初始值。
结论:权重必须随机生成初始值。
核心目标:我们希望各层的激活值(激活函数的输出数据)的分布有适当的广度,因为通过在各层间传递多样性的数据,神经网络可以进行高效的学习。
- 初始化权重:通过初始化权重实现,各层的激活分布会有适当的广度
- Batch Normalization:为了使各层拥有适当的广度,强制性调整激活值得分布
Xavier初始化(常用)
思路:通过调整权重的初始范围,使得每一层输出的方差保持一致,从而避免梯度消失或爆炸。
目标:保持前向传播时激活值的方差和反向传播时梯度的方差尽可能稳定。
这里的 n i n n_{in} nin表示前一层的神经元数量(当前层的输入), n o u t n_{out} nout表示当前层的神经元数量(当前层的输出)
- 初始化的权重值从均与分布中采样,范围为 ( − 6 n i n + n o u t , 6 n i n + n o u t ) (-\sqrt \frac{6}{n_{in}+n_{out}},\sqrt \frac{6}{n_{in}+n_{out}}) (−nin+nout6,nin+nout6)
- 初始化的权重值从高斯分布中采样,范围为 ( 0 , 2 n i n + n o u t ) (0,\sqrt \frac{2}{n_{in}+n_{out}}) (0,nin+nout2)
适用范围
激活函数在0点附近具有对称性(并不严格对称,而是保证正负信号均衡处理),且在0点附近呈线性,比如 sigmoid、tanh、softsign 等。

He初始化/Kaiming方法
思路:通过调整权重的初始范围,使得每一层输出的方差保持一致,从而避免梯度消失或爆炸。
这里的 n i n n_{in} nin表示前一层的神经元数量(当前层的输入), n o u t n_{out} nout表示当前层的神经元数量(当前层的输出)
- 初始化的权重值从均与分布中采样,范围为 ( − 6 n i n , 6 n i n ) (-\sqrt \frac{6}{n_{in}},\sqrt \frac{6}{n_{in}}) (−nin6,nin6)
- 初始化的权重值从高斯分布中采样,范围为 ( 0 , 2 n i n ) (0, \sqrt \frac{2}{n_{in}}) (0,nin2)
适用场景:ReLU函数
ReLU 函数会将大约一半的神经元输出设为零,因此需要更大的初始值来补偿这部分衰减。

Batch Normalization
思路:调整各层的激活值分布使其拥有适当的广度
做法:在神经网络中插入对数据分布进行正规化的层(Batch Normalization层)
算法
- 对mini=batch m个输入数据的集合 B = { x 1 , x 2 , . . . , x m } B=\{x_1,x_2,...,x_m\} B={x1,x2,...,xm}进行均值为0,方差为1(或者其他合适的分布)的正规化,通常将这个处理插入到激活函数的前面(后面),可以较小数据分布的偏向。
均值: μ B = 1 m ∑ i = 1 m x i μ_B=\frac{1}{m}\sum_{i=1}^mx_i μB=m1∑i=1mxi,方差: σ B 2 = 1 m ∑ i = 1 m ( x i − μ B ) 2 σ_B^2=\frac{1}{m}\sum_{i=1}^m(x_i-μ_B)^2 σB2=m1∑i=1m(xi−μB)2,归一化 x ^ i = ( x i − μ B ) σ B 2 + ε \hat x_i=\frac{(x_i-μ_B)}{\sqrt σ_B^2+ε} x^i=σB2+ε(xi−μB)
这里 ε ε ε是一个微小值(数值稳定性因子),目的是防止出现除以0的情况。
- Batch Norm层会对正规化后的数据进行缩放和平移变换 y i = γ x ^ i + β y_i=γ\hat x_i+β yi=γx^i+β
一开始 γ = 1 , β = 0 γ=1,β=0 γ=1,β=0,再通过学习调整到合适的值。
几乎所有的情况下都是使用Batch Norm时学习得更快,再不适用Batch Norm得情况下,如果赋予一个尺度好的初始值,学习将完全无法进行。
通过使用Batch Norm可以推动学习的进行,对权重初始化变得健壮(不那么依赖)。
Q&A
问题:如果在训练得过程中出现nan,时发生了梯度爆炸吗?
回答:一般是梯度爆炸导致的。
问题:梯度消失可以说是因为使用了sigmoid激活函数引起的吗?可以用ReLU替换sigmoid解决梯度消失问题吗?
回答:sigmoid容易引起梯度消失,梯度消失可能由其他原因产生的。使用ReLU可以让梯度消失的概率降低。
问题:梯度爆炸由什么激活函数引起
回答:一般梯度爆炸不是由激活函数(比较平滑)引起的,梯度爆炸一般是每个层的输出太大。
问题:强制使得每一层的输出特征均值为0,方差为1,是不是损失了网络的表达能力,改变了数据的特征?会降低学到的模型的准确度。
回答:数值是一个区间,在深度学习中数值范围本身并不承载语义信息,而是表达相对关系的方式。放缩都没关系,这个区间只是适合硬件。
相关文章:

李沐《动手学深度学习》 | 数值稳定性
文章目录 数值稳定性梯度消失Sigmoid作为激活函数 梯度爆炸 让训练更加稳定合理的权重初始化Xavier初始化(常用)He初始化/Kaiming方法 Batch Normalization Q&A 数值稳定性 当神经网络的深度比较深时,非常容易数值不稳定。 不稳定梯度是…...

OpenCV CUDA模块图像处理------图像连通域标记接口函数connectedComponents()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 该函数在 GPU 上执行二值图像的连通域标记操作,即将图像中所有相连的前景像素区域赋予相同的标签(label)&…...
Android Studio 打包时遇到了签名报错问题:Invalid keystore format
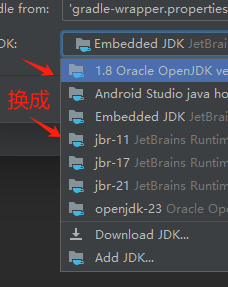
错误指出密钥库的格式无效,可能是由于密钥库本身的问题导致的,还有一种可能是由于jdk版本导致。我试过重新签名,也是不行,后来发现是JDK版本问题,我的Studio之前是jbr11,好像后来合并代码重新下载编译了项目…...

内存管理【Linux操作系统】
文章目录 简单谈一下物理内存管理页框为什么要把物理内存划分成一个一个固定大小的页框使用?对页框进行描述对页框进行组织管理虚拟地址→物理地址(真实的页表)真实的页表那我们如何把虚拟地址→物理地址呢?页表懒加载时ÿ…...

Go语言学习-->从零开始搭建环境
Go语言学习–>从零开始搭建环境 1 开发环境 Go官网下载地址:https://golang.org/dl/ Go官方镜像站(推荐):https://golang.google.cn/dl/ windos 平台下载: 我这里下载1.22稳定版 双击下载好的.msi文件 修改安装…...

【力扣】3403. 从盒子中找出字典序最大的字符串 I
解法一: class Solution {public String answerString(String word, int numFriends) {//对字符的划分,word长度为n,共有n1个位置可以插入,但是要求被分为非空字符串,所以插入的位置最多为n-1。int n word.length();…...

苹果企业签名撤销
苹果企业签名证书被撤销的原因通常涉及违反苹果的**《Apple Developer Program企业协议》**或相关安全政策,以下是常见原因: ### 一、核心违规原因 1. **证书滥用分发公开应用** * 企业证书仅限**内部员工使用**,若用于以下场景会被撤销&…...

12306高并发计算架构揭秘:Apache Geode 客户端接入与实践
目录 Apache Geode 客户端入门指南 一、安装 Apache Geode 二、启动 Geode 集群 三、Java 客户端接入 Geode Maven 示例依赖 Gradle 示例依赖 Java 示例代码 四、Spring Boot 客户端接入 Geode Maven 配置 Gradle 配置 运行应用 五、Apache Geode 原生客户端 .NET…...

JSON to Excel 3.0.0 版本发布 - 从Excel插件到Web应用的转变
1. 简介 JSON to Excel 3.0.0 是一个重大更新版本,将原有的Excel插件扩展为完整的Web应用。现在您可以直接在浏览器中使用它,无需安装任何插件。所有的转换在浏览器中完成,预览后,可点击下载按钮,导出成xlsx格式文件。…...

【前端】Vue3+elementui+ts,给标签设置样式属性style时,提示type check failed for prop,再次请出DeepSeek来解答
🌹欢迎来到《小5讲堂》🌹 🌹这是《前端》系列文章,每篇文章将以博主理解的角度展开讲解。🌹 🌹温馨提示:博主能力有限,理解水平有限,若有不对之处望指正!&…...

Neo4j 监控全解析:原理、技术、技巧与最佳实践
高效的监控是保障 Neo4j 图数据库性能、稳定性和可观察性的基石。本文将深入探讨 Neo4j 监控的核心原理、关键技术、实用技巧及行业最佳实践,助您构建强大的数据库运维体系。 掌握这些监控技术,将使您的 Neo4j 数据库在稳定性、性能和可维护性上达到企业…...

PyTorch——优化器(9)
优化器根据梯度调整参数,以达到降低误差 import torch.optim import torchvision from torch import nn from torch.nn import Sequential, Conv2d, MaxPool2d, Flatten, Linear from torch.utils.data import DataLoader# 加载CIFAR10测试数据集,设置tr…...

07 APP 自动化- appium+pytest+allure框架封装
文章目录 一、PO二、代码简单实现项目框架预览:base_page.pydir_config.pyget_data.pylogger.pystart_session.pyconfig.yamlkey_code.yamllaunch_page_loc.pylogin_page_loc.pylaunch_page.pylogin_page.pytest_login.pypytest.inirun.py 一、PO PO 分为四层 &…...

Postgresql常规SQL语句操作
目录 一、数据库与对象管理 二、数据操作 (CRUD) 三、查询优化与执行计划分析 四、事务控制 五、数据类型与高级特性应用 六、系统查询与维护 研发中的重要注意事项 在 PostgreSQL 研发中,以下这些 SQL 应用是极其常见且核心的操作,涵盖了数据库设…...

智能合约安全漏洞解析:从 Reentrancy 到 Integer Overflow
目录 🌀 Reentrancy(重入攻击) 原理解析 典型案例:The DAO 攻击事件 漏洞示例 防范措施 🔢 Integer Overflow(整数溢出) 原理解析 漏洞示例 防范措施 🛡️ 总结与建议 随着…...

英国2025年战略防御评估报告:网络与电磁域成现代战争核心
英国 2025 年战略防御评估 (SDR) 详细制定了一项计划,通过加强使用网络、人工智能和数字战争来整合其军事防御和进攻能力。 与美国一样,英国也被认为(尽管未被公开证实)会开展进攻性网络行动,甚至针对盟友。斯诺登泄露…...

基于QPSK调制解调+Polar编译码(SCL译码)的matlab性能仿真,并对比BPSK
目录 1.引言 2.算法仿真效果演示 3.数据集格式或算法参数简介 4.MATLAB核心程序 5.算法涉及理论知识概要 6.参考文献 7.完整算法代码文件获得 1.引言 Polar码由土耳其教授Erdal Arikan于2008年提出,是第一种被严格证明可以达到香农极限的构造性编码方法。其核…...

go语言学习 第5章:函数
第5章:函数 函数是编程中不可或缺的一部分,它封装了一段可重复使用的代码,用于执行特定的任务。在Go语言中,函数同样扮演着重要的角色。本章将详细介绍Go语言中函数的定义、调用、参数传递、返回值处理以及一些高级特性ÿ…...

Qt Quick快速入门笔记
Qt Quick快速入门笔记 基本的程序结构int main(int argc, char *argv[]) { #if QT_VERSION < QT_VERSION_CHECK(6, 0, 0)QCoreApplication::setAttribute(Qt::AA_EnableHighDpiScaling); #endifQGuiApplication app(argc, argv);QQmlApplicationEngine engine;const QUrl ur…...

《波段操盘实战技法》速读笔记
文章目录 书籍信息概览实战八法波段见顶信号中长线大顶形态投资理念 书籍信息 书名:《波段操盘实战技法》 作者:何瑞东 概览 实战八法 投资理念和投资理论概述:波段操作的核心是通过捕捉股价波动中的趋势性机会,结合技术分析与…...

Glide NoResultEncoderAvailableException异常解决
首先将解决方法提出来:缓存策略DiskCacheStrategy.DATA。 使用Glide加载图片,版本是4.15.0,有天发现无法显示gif图片,原始代码如下: Glide.with(context).load(本地资源路径).diskCacheStrategy(DiskCacheStrategy.A…...

工厂模式与多态结合
工厂模式与多态的结合是平台化项目中实现灵活架构的核心技术之一。这种组合能够创建可扩展、易维护的系统架构。 多态(Polymorphism)指同一操作作用于不同的对象,可以有不同的解释,产生不同的执行结果。 例子1: public abstract class Pay…...

无人机巡检智能边缘计算终端技术方案——基于EFISH-SCB-RK3588工控机/SAIL-RK3588核心板的国产化替代方案
一、方案核心价值 实时AI处理:6TOPS NPU实现无人机影像的实时缺陷检测(延迟<50ms)全国产化:芯片、操作系统、算法工具链100%自主可控极端环境适配:-40℃~85℃稳定运行,IP65防护等…...
相机--相机成像原理和基础概念
教程 成像原理 基础概念 焦距(物理焦距) 镜头的光学中心到感光元件之间的距离,用f表示,单位:mm;。 像素焦距 相机内参矩阵中的 fx 和 fy 是将物理焦距转换到像素坐标系的产物,可能不同。…...

2025-0604学习记录17——文献阅读与分享(2)
最近不是失踪了!也不是弃坑了...这不是马上要毕业了嘛!所以最近在忙毕业论文答辩、毕业去向填报、户档去向填报等等,事情太多了,没顾得上博客。现在这些事基本上都解决完了,也有时间静下心来写写文字了~ 想要写的内容…...

图解浏览器多进程渲染:从DNS到GPU合成的完整旅程
目录 浅谈浏览器进程 浏览器进程架构的演化 进程和线程关系图示 进程(Process) 线程(Thread) 协程(Coroutine) 进程&线程&协程核心对比 单进程和多进程浏览器 单进程浏览器编辑 单进程…...

【计算机网络】第3章:传输层—TCP 拥塞控制
目录 一、PPT 二、总结 TCP 拥塞控制详解 ⭐ 核心机制与算法 1. 慢启动(Slow Start) 2. 拥塞避免(Congestion Avoidance) 3. 快速重传(Fast Retransmit) 4. 快速恢复(Fast Recovery&…...

idea不识别lombok---实体类报没有getter方法
介绍 本篇文章,主要讲idea引入lombok后,在实体类中加注解Data,在项目启动的时候,编译不通过,报错xxx.java没有getXxxx()方法。 原因有以下几种 1. idea没有开启lombok插件 2. 使用idea-2023…...

【Hive入门】
之前实习写的笔记,上传留个备份。 1. 使用docker-compose快速搭建Hive集群 使用docker快速配置Hive环境 拉取镜像 2. Hive数据类型 隐式转换:窄的可以向宽的转换显式转换:cast 3. Hive读写文件 SerDe:序列化(对象转为字节码…...

亚马逊站内信规则2025年重大更新:避坑指南与合规策略
亚马逊近期对Buyer-Seller Messaging(买家-卖家站内信)规则进行了显著收紧,明确将一些曾经的“灰色操作”列为违规。违规操作轻则收到警告,重则导致账户暂停或绩效受限。本文为您全面解析本次规则更新的核心要点、背后逻辑&#x…...
