蜜獾算法(HBA,Honey Badger Algorithm)
2021年由Hashim等人提出(论文:Honey Badger Algorithm: A New Metaheuristic Algorithm for Solving Optimization Problems)。模拟蜜獾在自然界中的智能捕食行为,属于群体智能优化算法(与粒子群PSO、遗传算法GA同属一类),适用于连续优化问题。
一 行为模型
蜜獾的两种主要行为驱动算法设计:
(1)挖掘模式:
针对地下猎物:通过嗅觉定位 + 动态挖掘路径。
(2)采蜜模式:
跟随导蜜鸟定位蜂巢 → 直接奔袭蜜源。
二 数学模型与迭代步骤
2.1关键变量定义:
蜜獾位置:候选解向量
猎物强度(I):
:个体
的目标函数值(如适应度)
:当前种群中最小和最大函数值,两者做差可以将
进行归一化处理。
:极小常数(防止分母为零)
上述公式代标强度的范围最大是1+,最小是
。
函数值 反映解的质量。优化问题中,
越小(化最小问题)表示解越优,更优解代表更接近全局最优解,代表与“猎物”的隐含距离更小,因此隐含距离越小,强度越小,接近程度越大。
| 个体 | 函数值 F(x)F(x)F(x) | 与最优解距离 | 计算强度 IiI_iIi | 强度 vs 距离关系 |
|---|---|---|---|---|
| A(最优) | 最近 | 强度最小 | ||
| B | 中等 | 强度中等 | ||
| C(最差) | 最远 | 强度最大 |
强度越小越好。
距离大 ⇒ F(xi)差 ⇒ (F(xi)−Fmin) ↑ ⇒ ↑ ⇒ 算法反馈:加大搜索步长
这种设计以极低计算代价实现了蜜獾“嗅到远距离猎物时采取更大动作”的生物智能模拟。
为什么不用几何距离?
避免高维距离计算、函数值差距能推广到离散/非几何空间,泛用性高、算法运行中已计算 ,复用数据无需额外开销,效率高。
2.2探索阶段(Exploration)- 气味扩散
基于猎物强度的全局搜索:
:当前最佳猎物位置
:控制搜索方向(±1随机切换)
:随机向量
:密度因子(随迭代递减)
强度的作用:
大(解质量差、距离远)→ 乘以
后步长增大 → 加强全局探索
小(解质量好、距离近)→ 乘以
后步长减小 → 精细局部开发
2.3开发阶段(Exploitation)- 精确捕食
局部挖掘(模拟蜜獾洞穴内捕猎):
:随机向量
:个体到猎物的距离
通过密度因子 动态平衡探索与开发:
( 为常数,
为当前迭代,
为最大迭代)
决策规则:若 (
为切换阈值),使用挖掘模式;否则使用采蜜模式。
三 实现方法
3.1过程示例
初始化种群位置 x_i, i=1,2,...,N
计算适应度值 F(x_i)
while t < T_max:更新密度因子 α计算猎物强度 I_ifor each 蜜獾个体:if rand < δ:执行探索阶段(气味扩散)else:执行开发阶段(挖掘捕食)更新当前位置 x_i计算新适应度 F(x_i)更新全局最优解 x_preyt = t + 1
返回最优解 x_prey
3.2参数设置
| 参数 | 意义 | 推荐值 |
|---|---|---|
| 种群规模 | 30~50 | |
| 模式切换阈值 | 0.8 | |
| 密度衰减常数 | 2.0 | |
| 最大迭代次数 | 100~500 |
3.3优势和局限性
| 优势 | 局限性 |
|---|---|
| 全局探索能力强(气味机制) | 对高维问题敏感 |
| 局部开发高效(动态密度因子) | 参数需经验调整(如δ) |
| 收敛速度快于传统算法(PSO等) | 易陷局部最优的改进变体 |
| 代码实现简单 |
四 应用场景
工程优化:结构设计、PID控制器调参
人工智能:神经网络超参数优化
能源管理:光伏阵列最大功率点跟踪(MPPT)
研究方向:离散化改进(如HBA-TSP)、多目标版本(MO-HBA)
五 在CEC2017测试函数集上使用HBA的python代码
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import MaxNLocatorclass HBA:def __init__(self, obj_func, dim=30, pop_size=100, max_iter=1000, lb=-100, ub=100, C=2, delta=0.8):"""蜜獾算法 (Honey Badger Algorithm)参数:obj_func -- 目标函数dim -- 问题维度pop_size -- 种群大小max_iter -- 最大迭代次数lb -- 变量下界ub -- 变量上界C -- 密度因子常数delta -- 模式切换阈值"""self.obj_func = obj_funcself.dim = dimself.pop_size = pop_sizeself.max_iter = max_iterself.lb = lbself.ub = ubself.C = Cself.delta = delta# 初始化种群self.positions = np.random.uniform(lb, ub, (pop_size, dim))self.fitness = np.zeros(pop_size)self.best_position = np.zeros(dim)self.best_fitness = np.infself.convergence_curve = np.zeros(max_iter)def evaluate(self):"""评估所有个体适应度"""for i in range(self.pop_size):self.fitness[i] = self.obj_func(self.positions[i])if self.fitness[i] < self.best_fitness:self.best_fitness = self.fitness[i]self.best_position = self.positions[i].copy()def optimize(self):"""执行优化过程"""self.evaluate() # 初始评估for t in range(self.max_iter):# 1. 计算猎物强度f_min = np.min(self.fitness)f_max = np.max(self.fitness)I = (self.fitness - f_min) / (f_max - f_min + 1e-25) # 避免除零I = 1 + I # 确保强度至少为1# 2. 更新密度因子alpha = self.C * np.exp(-t / self.max_iter)# 3. 更新每个个体位置for i in range(self.pop_size):# 为每个个体生成随机方向因子F = 1 if np.random.rand() < 0.5 else -1 # 随机方向(在循环内部重新定义)if np.random.rand() < self.delta: # 挖掘模式(探索)r1, r2, r3 = np.random.rand(3) # 只需要3个随机数# 气味导向的位置更新new_pos = self.best_position + F * r1 * alpha * I[i] * \np.abs(np.cos(2 * np.pi * r2) * (1 - np.cos(2 * np.pi * r3)))else: # 采蜜模式(开发)r4 = np.random.rand()# 动态挖掘的位置更新new_pos = self.best_position + F * r4 * alpha * np.abs(self.best_position - self.positions[i])# 越界处理new_pos = np.clip(new_pos, self.lb, self.ub)# 计算新位置适应度new_fitness = self.obj_func(new_pos)# 更新个体位置和适应度if new_fitness < self.fitness[i]:self.positions[i] = new_posself.fitness[i] = new_fitnessif new_fitness < self.best_fitness:self.best_position = new_pos.copy()self.best_fitness = new_fitness# 记录当前最优解self.convergence_curve[t] = self.best_fitnessprint(f"Iteration {t + 1}/{self.max_iter} - Best Fitness: {self.best_fitness:.6e}")return self.best_position, self.best_fitness, self.convergence_curve# ===================== CEC2017测试函数集实现 ========================
def cec17_f1(x):"""Shifted and Rotated Bent Cigar Function (Function 1)"""d = len(x)z = x - 100 # Shift to new optimumrotated_z = z @ rot_matrix[d] if d in rot_matrix else z # Rotationreturn rotated_z[0] ** 2 + 1e6 * np.sum(rotated_z[1:] ** 2) + 100def cec17_f3(x):"""Shifted and Rotated Rosenbrock's Function (Function 3)"""d = len(x)z = 0.5 * (x - 40) # Shift and scalerotated_z = z @ rot_matrix[d] if d in rot_matrix else z # Rotationsum_val = 0for i in range(d - 1):sum_val += 100 * (rotated_z[i] ** 2 - rotated_z[i + 1]) ** 2 + (rotated_z[i] - 1) ** 2return sum_val + 300def cec17_f5(x):"""Shifted and Rotated Ackley's Function (Function 5)"""d = len(x)z = x + 50 # Shift to new optimumrotated_z = (z @ rot_matrix[d]) if d in rot_matrix else z # Rotationsum1 = np.sum(rotated_z ** 2)sum2 = np.sum(np.cos(2 * np.pi * rotated_z))return -20 * np.exp(-0.2 * np.sqrt(sum1 / d)) - np.exp(sum2 / d) + 20 + np.e + 500# ===================== 辅助函数 ========================
def generate_rotation_matrix(dim):"""生成随机旋转矩阵(模拟CEC2017的旋转特性)"""H = np.random.randn(dim, dim)Q, R = np.linalg.qr(H)return Qdef plot_results(convergence, func_name, dim):"""绘制收敛曲线"""plt.figure(figsize=(10, 6))plt.semilogy(convergence, 'b-', linewidth=2)plt.title(f'HBA on {func_name} - Dimension {dim}\nFinal Fitness: {convergence[-1]:.4e}', fontsize=12)plt.xlabel('Iteration', fontsize=12)plt.ylabel('Fitness (log scale)', fontsize=12)plt.grid(True, which='both', linestyle='--')plt.gca().xaxis.set_major_locator(MaxNLocator(integer=True))plt.tight_layout()plt.show()# ===================== 主程序 ========================
if __name__ == "__main__":# 实验参数dim = 30 # 问题维度max_iter = 1000 # 最大迭代次数pop_size = 100 # 种群大小# 预生成旋转矩阵 (模拟CEC2017特性)np.random.seed(42)rot_matrix = {dim: generate_rotation_matrix(dim)}# 定义要测试的函数test_functions = {"CEC2017 F1 (Bent Cigar)": cec17_f1,"CEC2017 F3 (Rosenbrock)": cec17_f3,"CEC2017 F5 (Ackley)": cec17_f5}# 对每个测试函数运行HBAresults = {}for name, func in test_functions.items():print(f"\n{'=' * 80}")print(f"Optimizing Function: {name}")print(f"{'=' * 80}")# 初始化并运行HBAoptimizer = HBA(obj_func=func,dim=dim,pop_size=pop_size,max_iter=max_iter,lb=-100,ub=100)best_sol, best_fit, convergence = optimizer.optimize()results[name] = convergence# 打印最终结果print(f"\n{'*' * 80}")print(f"{name} Optimization Result:")print(f"Best Solution: {best_sol[:5]}...") # 只打印前5维print(f"Best Fitness: {best_fit:.6e}")print(f"Optimal Value Found: {func(best_sol):.6e}")print(f"{'*' * 80}\n")# 绘制收敛曲线plot_results(convergence, name, dim)# 比较所有函数的收敛曲线plt.figure(figsize=(12, 8))for name, conv in results.items():plt.semilogy(conv, label=name, linewidth=2)plt.title(f'HBA Performance on CEC2017 Functions (Dim={dim})', fontsize=16)plt.xlabel('Iteration', fontsize=12)plt.ylabel('Fitness (log scale)', fontsize=12)plt.legend(fontsize=12)plt.grid(True, which='both', linestyle='--')plt.tight_layout()plt.savefig('hba_cec2017_convergence.png', dpi=300)plt.show()
输出值为:


 通过增加迭代次数和种群大小可以更加接近最优解。
通过增加迭代次数和种群大小可以更加接近最优解。



相关文章:

蜜獾算法(HBA,Honey Badger Algorithm)
2021年由Hashim等人提出(论文:Honey Badger Algorithm: A New Metaheuristic Algorithm for Solving Optimization Problems)。模拟蜜獾在自然界中的智能捕食行为,属于群体智能优化算法(与粒子群PSO、遗传算法GA同属一…...

Modbus转Ethernet IP网关助力罗克韦尔PLC数据交互
在工业自动化领域,Modbus协议是一种广泛应用的串行通信协议,它定义了主站和从站之间的通信规则和数据格式。罗克韦尔PLC是一种可编程的逻辑控制器,通过Modbus协议实现与其他设备之间的数据交互。然而,随着以太网技术的普及和发展&…...

飞算JavaAI 炫技赛重磅回归!用智能编码攻克老项目重构难题
深夜还在排查十年前Hibernate框架埋下的N1查询隐患?跨语言迁移时发现SpringMVC控制器里的业务逻辑像一团乱麻?当企业数字化进入深水区,百万行代码的老系统就像一座随时可能崩塌的"技术债冰山"。近日,飞算科技发布JavaAI…...

青少年编程与数学 02-020 C#程序设计基础 15课题、异常处理
青少年编程与数学 02-020 C#程序设计基础 15课题、异常处理 一、异常1. 异常的分类2. 异常的作用小结 二、异常处理1. 异常处理的定义2. 异常处理的主要组成部分3. 异常处理的作用小结 三、C#异常处理1. 异常的基本概念2. 异常处理的关键字3. 异常处理的流程4. 自定义异常5. 异…...

Electron打包前端和后端为exe
文章目录 什么是Electron? 安装electron过程 其他git项目地址比较好的文章electron的替代品安装报错 npm ERR! request to https://registry.npm.taobao.org/electron failed, reason: certificate has expired安装提示 npm WARN deprecated boolean3.2.0: Package …...
的身份来执行命令)
unix/linux,sudo,一个强大且灵活的工具,允许一个被授权的用户以另一个用户(通常是root,即超级用户)的身份来执行命令
sudo:不仅仅是“用管理员权限运行” sudo 这个词,来源于 SuperUser DO (或者 Substitute User DO,后者的含义更为广阔和准确)。它是一个强大且灵活的工具,允许一个被授权的用户以另一个用户(通常是root,即超级用户)的身份来执行命令。 1. Unix/Linux 的权限哲学:最小…...
 是个大坑?)
JavaScript 二维数组初始化:为什么 fill([]) 是个大坑?
JavaScript 二维数组初始化:为什么 fill([]) 是个大坑? 今天刷leetcode的时候,遇到一个神奇的bug。 当我修改数组中的一个元素,却意外影响了其他所有元素???。 问题重现:诡异的数组…...

项目任务,修改svip用户的存储空间。
修改存储空间 3GB->5GB,这是项目任务,首先有人任务就要去思考实现思路,首先存储空间,也就是说不只是前端样式3GB改一下就可以了,那用户实际还是3GB,所以我们去网站看后端谁返回给我们了3GB,我…...
)
TypeScript 全面学习指南 (2025最新版)
TypeScript 全面学习指南 目录 TypeScript 简介环境搭建与工具基础类型变量声明接口(Interfaces)类(Classes)函数(Functions)泛型(Generics)枚举(Enums)类型…...

【redis】过期策略 懒惰删除
过期删除: redis会将所有设置过期时间的key以及过期时间存储在字典里。 redis采取两个策略实现删除过期key: 1、定时删除:定期扫描字典,采用贪心的策略,从字典随机抽20个key,删除其中已经过期的key&#x…...

Docker或Docker-Compose时间时区配置
Docker或Docker-Compose配置时区,主要是为了使用容器内的时间和物理机操作系统的时间保持一致。以下是集中配置Docker或Docker-Compose环境时间时区的方式。 Dockerfile(Docker)中配置时区 在Dockerfile中,可以通过如下方式添加…...

如何在IDE中通过Spark操作Hive
在IDE中通过Spark操作Hive是一项常见的任务,特别是在大数据处理和分析的场景中。本文将详细介绍如何在集成开发环境(IDE)中使用Apache Spark与Hive进行交互,包括必要的设置、代码示例以及详细解释。 环境准备 在开始之前&#x…...

ToolsSet之:XML工具
ToolsSet是微软商店中的一款包含数十种实用工具数百种细分功能的工具集合应用,应用基本功能介绍可以查看以下文章: Windows应用ToolsSet介绍https://blog.csdn.net/BinField/article/details/145898264 ToolsSet中Text菜单下的XML Tool工具是一个Xml工…...

keepalived定制日志bug
keepalived定制日志bug 源码安装apt安装endl 源码安装 在/etc/rsyslog.d/目录下创建 keepalived的日志配置文件keepalived.conf [rootubuntu24-13:~]# vim /etc/rsyslog.d/keepalived.conf [rootubuntu24-13:~]# cat /etc/rsyslog.d/keepalived.conf local6.* /var/log/keepa…...

ElasticSearch+Gin+Gorm简单示例
更多个人笔记见: (注意点击“继续”,而不是“发现新项目”) github个人笔记仓库 https://github.com/ZHLOVEYY/IT_note gitee 个人笔记仓库 https://gitee.com/harryhack/it_note 个人学习,学习过程中还会不断补充&…...

数据库系统概论(十三)详细讲解SQL中数据更新(插入,修改与更新)
数据库系统概论(十三)详细讲解SQL中数据更新 前言一、数据插入1. 插入数据是什么?2.插入单条数据(插入元组)场景 1:指定部分列插入场景 2:不指定列名(插入所有列)场景 3&…...

JVMTI 在安卓逆向工程中的应用
JVMTI 在安卓逆向工程中的应用 JVMTI 在安卓逆向工程中扮演着重要角色,尤其是在分析和修改 Java 层应用行为时。以下是其核心应用场景、实现方式及典型工具: 一、核心应用场景 1. 动态代码注入与 hook 通过 JVMTI 可以在运行时修改或拦截 Java 方法&…...
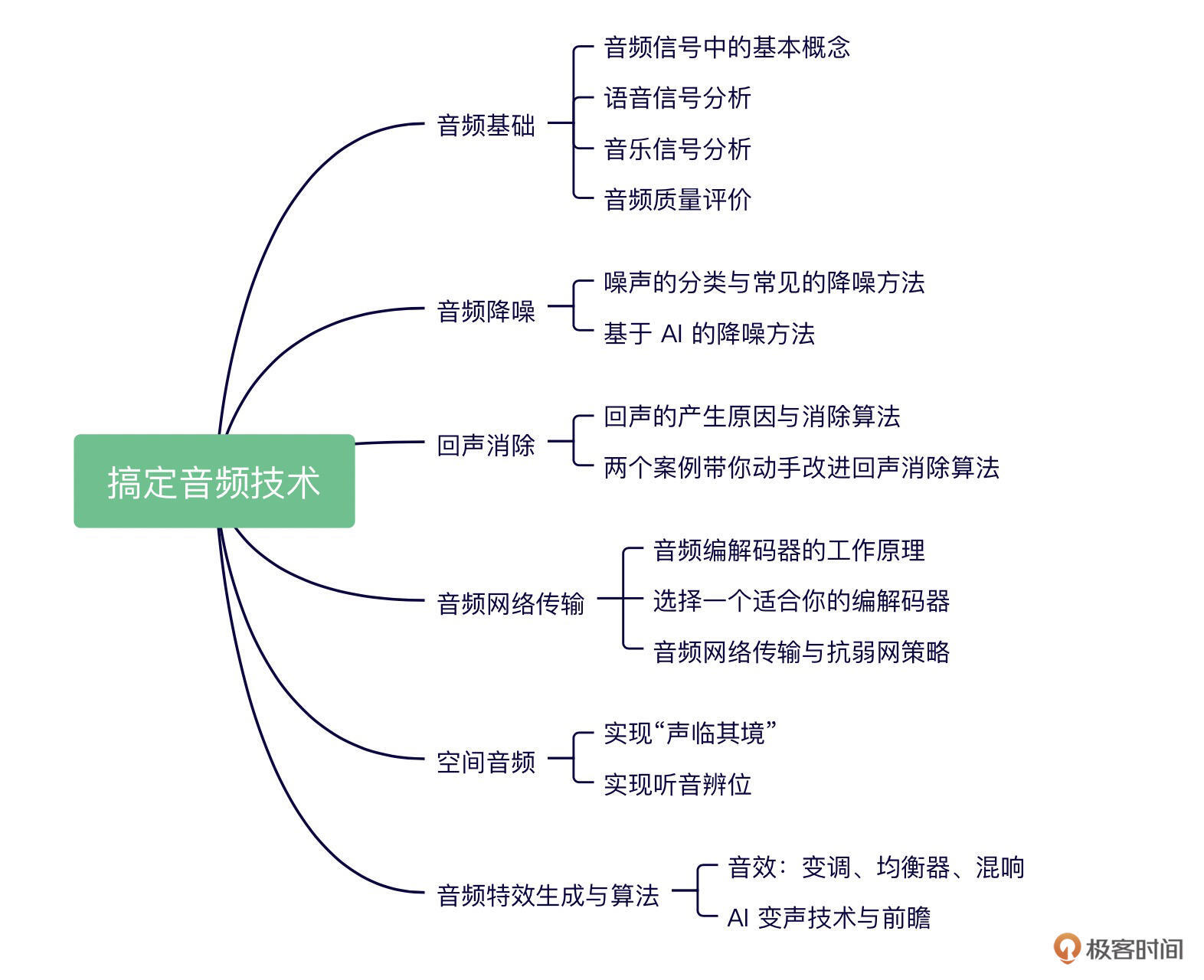
极客时间-《搞定音频技术》-学习笔记
极客时间-《搞定音频技术》-学习笔记 语音基础知识 https://www.zhangzhenhu.com/audio/feature.html 序章-0 作者说这个语音技术啊,未来肯定前景大好啊,大家都来学习,然后给出了课程的脑图 音频基础 什么是声音 声音的三要素是指响度、…...

网络攻防技术十三:网络防火墙
文章目录 一、网络防火墙概述1、网络型防火墙(网络防火墙)2、Web应用防火墙3、数据库防火墙4、主机防火墙(个人防火墙)5、网络防火墙的功能 二、防火墙工作原理1、无状态包过滤防火墙2、有状态包过滤防火墙(状态检测/动…...

Express 集成Sequelize+Sqlite3 默认开启WAL 进程间通信 Conf 打包成可执行 exe 文件
代码:express-exe: 将Express开发的js打包成exe服务丢给客户端使用 实现目标 Express 集成 Sequelize 操作 Sqlite3 数据库; 启动 Sqlite3 时默认开启 WAL 模式,避免读写互锁,支持并发读; 利用 Conf 实现主进程与 Ex…...

CppCon 2015 学习:A C++14 Approach to Dates and Times
Big Picture — 日期库简介 扩展 标准库 这个库是对 C 标准库中 <chrono> 的自然延伸,专注于处理“日历”相关的功能(比如年月日、闰年、节假日等),而不仅仅是时间点和时长。极简设计 它是**单头文件(header-on…...

基于CNN的OFDM-IM信号检测系统设计与实现
基于CNN的OFDM-IM信号检测系统设计与实现 摘要 本文详细研究了基于卷积神经网络(CNN)的正交频分复用索引调制(OFDM-IM)信号检测方法。通过在不同信噪比(SNR)和信道条件下进行系统仿真,对比分析了CNN检测器与传统最大似然(ML)检测器的误码率(BER)性能和计算复杂度。实验结果表…...
)
macos常见且应该避免被覆盖的系统环境变量(避免用 USERNAME 作为你的自定义变量名)
文章目录 macos避免用 USERNAME 作为你的自定义变量名macos常见且应该避免被覆盖的系统环境变量 macos避免用 USERNAME 作为你的自定义变量名 问题: 你执行了:export USERNAME“admin” 然后执行:echo ${USERNAME} 输出却是:xxx …...

2024年认证杯SPSSPRO杯数学建模D题(第二阶段)AI绘画带来的挑战解题全过程文档及程序
2024年认证杯SPSSPRO杯数学建模 D题 AI绘画带来的挑战 原题再现: 2023 年开年,ChatGPT 作为一款聊天型AI工具,成为了超越疫情的热门词条;而在AI的另一个分支——绘图领域,一款名为Midjourney(MJÿ…...

深入理解CSS常规流布局
引言 在网页设计中,理解元素如何排列和相互作用至关重要。CSS提供了三种主要的布局方式:常规流、浮动和定位。本文将重点探讨最基础也是最常用的常规流布局(Normal Flow),帮助开发者掌握页面布局的核心机制。 什么是…...

DOCKER使用记录
1、拉取镜像 直接使用docker pull <image>,大概率会出现下面的报错信息: (base) jetsonyahboom:~$ docker pull ubuntu:18.04 Error response from daemon: Get "https://registry-1.docker.io/v2/": net/http: request canceled while …...

MYSQL中常见的函数和使用
字符串函数 CONCAT(str1,str2,...,strN) :用于将多个字符串连接成一个字符串。例如,SELECT CONCAT(SQL, , 函数) ,结果为 “SQL 函数”。 LOWER(str) :将字符串中的所有字母转换为小写。例如,SELECT LOWER(MySQL Fun…...

【深度学习相关安装及配环境】Anaconda搭建虚拟环境并安装CUDA、cuDVV和对应版本的Pytorch,并在jupyter notebook上部署
目录 1. 查看自己电脑的cuda版本2.安装cuda关于环境变量的配置测试一下,安装完成 3.安装cuDVV环境变量的配置测试一下,安装完成 4.创建虚拟环境先安装镜像源下载3.11版本py 5.在虚拟环境下,下载pytorch6.验证是否安装成功7.在jupyter noteboo…...

web3-区块链基础:从区块添加机制到哈希加密与默克尔树结构
区块链基础:从区块添加机制到哈希加密与默克尔树结构 什么是区块链 抽象的回答: 区块链提供了一种让多个参与方在没有一个唯一可信方的情况下达成合作 若有可信第三方 > 不需要区块链 [金融系统中常常没有可信的参与方] 像股票市场,或者一个国家的…...

TCP小结
1. 核心特性 面向连接:通过三次握手建立连接,四次挥手终止连接,确保通信双方状态同步。 TCP连接建立的3次握手 抓包: client发出连接请求; server回应client请求,并且同步发送syn连接; clien…...
