策略梯度核心:Advantage 与 GAE 原理详解
一.Advantage(优势函数)详解
什么是 Advantage?
Advantage 表示当前动作比平均水平好多少。
其定义公式为:
A ( s , a ) = Q ( s , a ) − V ( s ) A(s, a) = Q(s, a) - V(s) A(s,a)=Q(s,a)−V(s)
其中:
- Q ( s , a ) Q(s, a) Q(s,a):在状态 s s s 下执行动作 a a a 所得到的期望回报
- V ( s ) V(s) V(s):在状态 s s s 下的平均期望回报
简而言之:
- 如果 A ( s , a ) > 0 A(s, a) > 0 A(s,a)>0,说明该动作比平均值好,应该增强其概率
- 如果 A ( s , a ) < 0 A(s, a) < 0 A(s,a)<0,说明该动作不好,应该削弱其概率
在策略梯度算法中的作用
在策略梯度方法(如 PPO、REINFORCE)中,优化目标常写为:
L ( θ ) = − log π θ ( a ∣ s ) ⋅ A ( s , a ) \mathcal{L}(\theta) = -\log \pi_\theta(a|s) \cdot A(s, a) L(θ)=−logπθ(a∣s)⋅A(s,a)
含义是:
- 当 Advantage 大时,增大该动作概率;
- 当 Advantage 小时,减小该动作概率;
- Advantage 起到了加权放大奖励信号的作用。
总结表格
| 项目 | 描述 |
|---|---|
| 定义 | 动作与当前状态平均价值的差异 |
| 数学表达 | A ( s , a ) = Q ( s , a ) − V ( s ) A(s, a) = Q(s, a) - V(s) A(s,a)=Q(s,a)−V(s) |
| 主要用途 | 用于衡量动作质量,指导策略梯度方向 |
| 使用场景 | PPO、REINFORCE、A2C、TRPO 等策略优化算法 |
| 是否关键 | 是策略更新的核心量,通常结合 GAE 进一步估算 |
二.GAE:Generalized Advantage Estimation
什么是 GAE?
GAE 是一种用于计算 Advantage(优势函数)的方法,目的是 在偏差和方差之间取得平衡,从而提高策略梯度算法(如 PPO、TRPO)的稳定性与收敛速度。
背景知识
回顾基本定义:
-
状态值函数: V ( s t ) V(s_t) V(st) 表示在状态 s t s_t st 下的期望回报。
-
优势函数: A ( s t , a t ) = Q ( s t , a t ) − V ( s t ) A(s_t, a_t) = Q(s_t, a_t) - V(s_t) A(st,at)=Q(st,at)−V(st),表示某动作比平均动作好多少。
-
TD误差(Temporal Difference Error):
δ t = r t + γ V ( s t + 1 ) − V ( s t ) \delta_t = r_t + \gamma V(s_{t+1}) - V(s_t) δt=rt+γV(st+1)−V(st)
GAE 的公式
GAE 使用加权和的形式累积多个时间步的 TD 误差:
A ^ t GAE ( γ , λ ) = ∑ l = 0 ∞ ( γ λ ) l δ t + l \hat{A}_t^{\text{GAE}(\gamma, \lambda)} = \sum_{l=0}^{\infty} (\gamma \lambda)^l \delta_{t+l} A^tGAE(γ,λ)=l=0∑∞(γλ)lδt+l
其中:
- δ t = r t + γ V ( s t + 1 ) − V ( s t ) \delta_t = r_t + \gamma V(s_{t+1}) - V(s_t) δt=rt+γV(st+1)−V(st) 是 TD 误差
- γ \gamma γ:折扣因子(控制未来奖励的重要性)
- λ \lambda λ:平滑因子(控制 bias vs. variance)
当 λ = 0 \lambda = 0 λ=0,只考虑一步 TD 误差(高偏低方);
当 λ → 1 \lambda \to 1 λ→1,接近 Monte Carlo(低偏高方);
GAE 的优势
| 特性 | 描述 |
|---|---|
| 降低方差 | 多步估计会平滑短期噪声 |
| 保持较小偏差 | 引入 λ \lambda λ 控制偏差 |
| 提高训练稳定性 | 在 PPO、TRPO 等算法中大幅提升收敛性能 |
| 易于实现 | 可用递推公式高效实现 |
递推公式(更高效)
实际中常用递推方式高效计算:
A ^ t = δ t + γ λ A ^ t + 1 \hat{A}_t = \delta_t + \gamma \lambda \hat{A}_{t+1} A^t=δt+γλA^t+1
从最后一个时间步开始反向计算,避免显式展开加权和。
总结
- GAE 是 TD 和 MC 方法之间的折中
- 关键控制参数是 λ \lambda λ,需调节其值以在 bias/variance 间权衡
- 是现代策略优化算法中的核心技术之一
📚 推荐论文:GAE 原始论文 by Schulman et al., 2016
相关文章:

策略梯度核心:Advantage 与 GAE 原理详解
一.Advantage(优势函数)详解 什么是 Advantage? Advantage 表示当前动作比平均水平好多少。 其定义公式为: A ( s , a ) Q ( s , a ) − V ( s ) A(s, a) Q(s, a) - V(s) A(s,a)Q(s,a)−V(s) 其中: Q ( s , a ) …...

Python 使用总结之:Python 文本转语音引擎 - pyttsx3 完全指南
文本转语音(TTS,Text-to-Speech)技术已经广泛应用于语音助手、智能硬件、教育软件等多个领域。Python 提供了多个库来实现 TTS,其中 pyttsx3 是一个非常常用的跨平台 TTS 引擎。本文将详细介绍如何使用 pyttsx3 实现文本转语音的功…...

星闪开发之Server-Client 指令交互控制红灯亮灭案例解析(SLE_LED详解)
系列文章目录 星闪开发之Server-Client 指令交互控制红灯亮灭的全流程解析(SLE_LED详解) 文章目录 系列文章目录前言一、项目地址二、客户端1.SLE_LED_Client\inc\SLE_LED_Client.h2.SLE_LED_Client\src\SLE_LED_Client.c头文件与依赖管理宏定义与全局变…...

day25-计算机网络-3
1. DNS解析流程 windows host文件是否配置域名对应的ip查询本地DNS缓存是否有这个域名对应的ip询问本地DNS(网卡配置的)是否知晓域名对应的ip本地DNS访问根域名解析服务器,但是根DNS只有顶级域名的记录,根告诉我们.cn顶级域名的D…...

【ArcGIS应用】ArcGIS应用如何进行影像分类?
ArcGIS应用如何进行影像分类?...
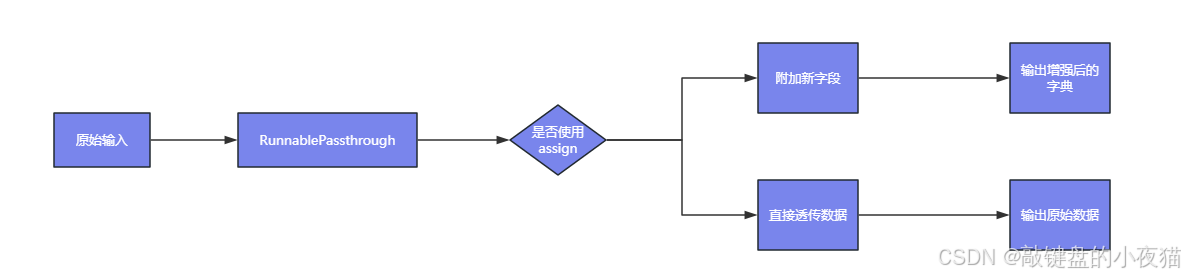
RunnablePassthrough介绍和透传参数实战
导读:在构建复杂的LangChain应用时,你是否遇到过需要在处理链中既保留原始输入又动态扩展上下文的场景?RunnablePassthrough正是为解决这类数据流处理问题而设计的核心组件。 本文通过深入剖析RunnablePassthrough的工作机制和实际应用&#…...

JavaSec-XSS
反射型XSS 简介 XSS(跨站脚本攻击)利用浏览器对服务器内容的信任,攻击者通过在网页中注入恶意脚本,使这些脚本在用户的浏览器上执行,从而实现攻击。常见的XSS攻击危害包括窃取用户会话信息、篡改网页内容、将用户重定向到恶意网站,…...

AtCoder-abc408_b 解析
题目链接 让我们一步一步详细分析这个问题: 题目要求我们实现去重并排序的功能,这在C中可以直接使用set容器来实现。set是STL中的一个关联容器,具有以下特性: 自动去重:所有元素都是唯一的自动排序:默认…...

echarts在uniapp中使用安卓真机运行时无法显示的问题
文章目录 一、实现效果二、话不多说,上源码 前言:我们在uniapp中开发的时候,开发的时候很正常,echarts的图形在h5页面上也是很正常的,但是当我们打包成安卓app或者使用安卓真机运行的时候,图形根本就没有渲…...

STM32----IAP远程升级
一、概述: IAP,全称是“In-Application Programming”,中文解释为“在程序中编程”。IAP是一种对通过微控制器的对外接口(如USART,IIC,CAN,USB,以太网接口甚至是无线射频通道&#…...

C++优选算法 904. 水果成篮
文章目录 1.题目描述2.算法思路 3.完整代码容器做法数组做法 1.题目描述 看到这种题目,总觉得自己在做阅读理解,晕了,题目要求我们在一个数组里分别找出两种数字,并统计这两种数字分别出现一共是多少。 2.算法思路 采用哈希表滑…...

Python6.5打卡(day37)
DAY 37 早停策略和模型权重的保存 知识点回顾: 过拟合的判断:测试集和训练集同步打印指标模型的保存和加载 仅保存权重保存权重和模型保存全部信息checkpoint,还包含训练状态 早停策略 作业:对信贷数据集训练后保存权重…...
大中型水闸安全监测管理系统建设方案
一、背景介绍 我国现已建成流量5m/s及以上的水闸共计100321座。其中,大型水闸923座,中型水闸6,697座。按功能类型划分,分洪闸8193座,排(退)水闸17808座,挡潮闸4955座,引水闸13796座&…...

Compose Multiplatform 实现自定义的系统托盘,解决托盘乱码问题
Compose Multiplatform是 JetBrains 开发的声明式 UI 框架,可让您为 Android、iOS、桌面和 Web 开发共享 UI。将 Compose Multiplatform 集成到您的 Kotlin Multiplatform 项目中,即可更快地交付您的应用和功能,而无需维护多个 UI 实现。 在…...

风控研发大数据学习路线
在如今信息爆炸时代,风控系统离不开大数据技术的支撑,大数据技术可以帮助风控系统跑的更快,算的更准。因此,风控技术研发需要掌握大数据相关技术。然而大数据技术栈内容庞大丰富,风控研发同学很可能会面临以下这些痛点…...

【设计模式】门面/外观模式
MySQL ,MyTomcat 的启动 现在有 MySQL ,MyTomcat 类,需要依次启动。 public class Application {public static void main(String[] args) {MySQL mySQL new MySQL();mySQL.initDate();mySQL.checkLog();mySQL.unlock();mySQL.listenPort(…...

spring的webclient与vertx的webclient的比较
Spring WebClient 和 Vert.x WebClient 都是基于响应式编程模型的非阻塞 HTTP 客户端,但在设计理念、生态整合和适用场景上存在显著差异。以下是两者的核心比较: 🔄 1. 技术背景与架构 • Spring WebClient ◦ 生态定位:属于 Sp…...

贪心算法应用:埃及分数问题详解
贪心算法与埃及分数问题详解 埃及分数(Egyptian Fractions)问题是数论中的经典问题,要求将一个真分数表示为互不相同的单位分数之和。本文将用2万字全面解析贪心算法在埃及分数问题中的应用,涵盖数学原理、算法设计、Java实现、优…...

高效集成AI能力:使用开放API打造问答系统,不用训练模型,也能做出懂知识的AI
本文为分享体验感受,非广告。 一、蓝耘平台核心功能与优势 丰富的模型资源库 蓝耘平台提供涵盖自然语言处理、计算机视觉、多模态交互等领域的预训练模型,支持用户直接调用或微调,无需从零开始训练,显著缩短开发周期。 高性能…...

Qt 仪表盘源码分享
Qt 仪表盘源码分享 一、效果展示二、优点三、源码分享四、使用方法 一、效果展示 二、优点 直观性 数据以图表或数字形式展示,一目了然。用户可以快速获取关键信息,无需深入阅读大量文字。 实时性 仪表盘通常支持实时更新,确保数据的时效性。…...

Python数据可视化科技图表绘制系列教程(四)
目录 带基线的棒棒糖图1 带基线的棒棒糖图2 带标记的棒棒糖图 哑铃图1 哑铃图2 包点图1 包点图2 雷达图1 雷达图2 交互式雷达图 【声明】:未经版权人书面许可,任何单位或个人不得以任何形式复制、发行、出租、改编、汇编、传播、展示或利用本博…...

RPM 数据库修复
RPM 数据库修复 1、备份当前数据库(重要!) sudo cp -a /var/lib/rpm /var/lib/rpm.backup此操作保护原始数据,防止修复失败导致数据丢失 2、清除损坏的锁文件 sudo rm -f /var/lib/rpm/__db.*这些锁文件(如 __db.00…...
)
R语言基础知识总结(超详细整理)
一、R语言简介 R是一种用于统计分析、数据可视化和科学计算的开源编程语言和环境。其语法简洁,内置丰富的统计函数和图形函数,广泛应用于数据科学、机器学习和生物统计等领域。 整体知识点目录: R语言基础知识总结 │ ├─ 安装与配置 │ …...

深入理解系统:UML类图
UML类图 类图(class diagram) 描述系统中的对象类型,以及存在于它们之间的各种静态关系。 正向工程(forward engineering)在编写代码之前画UML图。 逆向工程(reverse engineering)从已有代码建…...

C# 中的 IRecipient
IRecipient<TMessage> 是 .NET 中消息传递机制的重要组成部分,特别是在 MVVM (Model-View-ViewModel) 模式中广泛使用。下面我将详细介绍这一机制及其应用。 基本概念 IRecipient<TMessage> 是 .NET Community Toolkit 和 MVVM Toolkit 中定义的一个接…...

大模型RNN
RNN(循环神经网络)是一种专门处理序列数据的神经网络架构,在自然语言处理(NLP)、语音识别、时间序列分析等领域有广泛应用。其核心作用是捕捉序列中的时序依赖关系,即当前输出不仅取决于当前输入࿰…...

Python环境搭建竞赛技术文章大纲
竞赛背景与意义 介绍Python在数据科学、机器学习等领域的重要性环境搭建对于竞赛项目效率的影响常见竞赛平台对Python环境的特殊要求 基础环境准备 操作系统选择与优化(Windows/Linux/macOS)Python版本选择(3.x推荐版本)解释器…...

Redisson - 实现延迟队列
Redisson 延迟队列 Redisson 是基于 Redis 的一款功能强大的 Java 客户端。它提供了诸如分布式锁、限流器、阻塞队列、延迟队列等高可用、高并发组件。 其中,RDelayedQueue 是对 Redis 数据结构的高阶封装,能让你将消息延迟一定时间后再进入消费队列。…...

软件工程的定义与发展历程
文章目录 一、软件工程的定义二、软件工程的发展历程1. 前软件工程时期(1940s-1960s)2. 软件工程诞生(1968)3. 结构化方法时期(1970s)4. 面向对象时期(1980s)5. 现代软件工程(1990s-至今) 三、软件工程的发展趋势 一、软件工程的定义 软件工程是应用系统化、规范化、可量化的方…...

艾利特协作机器人:重新定义工业涂胶场景的精度革命
品牌使命与技术基因 作为全球协作机器人领域成长最快的企业之一,艾利特始终聚焦于解决工业生产中的人机协作痛点。在汽车制造、3C电子、新能源等领域的涂胶工艺场景中,我们通过自主研发的EC系列协作机器人,实现了: 空间利用率&a…...
