35.x64汇编写法(二)
免责声明:内容仅供学习参考,请合法利用知识,禁止进行违法犯罪活动!
本次游戏没法给
内容参考于:微尘网络安全
上一个内容:34.x64汇编写法(一)
上一个内容写了,汇编调用c标准库里的getchar函数,这次写的是c调用汇编
首先说明一下 extern 这个单词,只要有 extern 这个单词就说明当前函数或变量是一个全局的,比如 extern int f; 这个代码,现在在文件1中写 extern int f; 然后文件2中也写 extern int f; ,文件1中把f的值设置成了10,然后在文件2中什么都不写,只写extern int f;这一句,此时f的值会是10,因为是全局的,文件1中的修改影响到了它,函数也一样(可能普通手段没办法修改函数,因为会语法不通过)
c代码
#include <iostream>// 带着 extern 这个单词就说明从全局中找,带着extern它的如果函数名重复了会出现问题
// 在全局中找一个 addShu ,这个addShu函数实用汇编实现的
extern "C" int addShu(int s1, int s2);
int main() {int num = addShu(11, 23);printf("num = %d", num);
}
汇编代码,addShu函数的实现
.codeaddShu procsub rsp, 100h ; 开辟栈xor rax, raxmov rax, rcx ; 获取第一个参数给raxadd rax, rdx ; 第一个参数与第二个参数进行相加add rsp, 100h ; 恢复栈ret ; 返回addShu endpend
效果图:

然后有一个问题,把num改成从全局的,并把它的值设置成999

汇编代码的修改,正常运行的话,它会返回999

实际上它返回的是 -1892892644

这里直接说答案-1892892644是num的内存地址,怎么发现通过断点,如下图设置断点(鼠标左键单击红色圆的位置就可以设置断点和取消断点)

运行后断点住

然后打开监视窗口

然后可以看到它们俩的值是正常的

然后点击下图红框位置,运行一行代码

然后看到rax的值并不是999

然后写一个 &num 表示取num的内存地址

然后鼠标右击选择以十六进制显示

然后就能发现rax的值是num的内存地址了

这个问题就是这里的mov变成了lea,所以要注意在使用全局变量赋值的时候,多写一句 mov rax,[rax]这样的代码,如下图红框

效果图:

汇编代码
extern num:far
.codeaddShu procsub rsp, 100h ; 开辟栈xor rax, raxmov rax, rcx ; 获取第一个参数给raxadd rax, rdx ; 第一个参数与第二个参数进行相加mov rax, num ; 获取全局变量nummov rax,[rax] ; 获取num的值add rsp, 100h ; 恢复栈ret ; 返回addShu endpend
c/c++代码
#include <iostream>// 带着 extern 这个单词就说明从全局中找,带着extern它的如果函数名重复了会出现问题
// 在全局中找一个 addShu ,这个addShu函数实用汇编实现的
extern "C" int addShu(int s1, int s2);
extern "C" int num = 999;
int main() {num = addShu(11, 23);printf("num = %d", num);
}

相关文章:

35.x64汇编写法(二)
免责声明:内容仅供学习参考,请合法利用知识,禁止进行违法犯罪活动! 本次游戏没法给 内容参考于:微尘网络安全 上一个内容:34.x64汇编写法(一) 上一个内容写了,汇编调…...

安全大模型的思考
马上要准备2025年的护网了,最近就一直很忙,被事情裹挟着前进,忙的晕头转向,近乎感冒,昨天部门搞了一场AI大模型培训,演讲者有着很深的技术底蕴,我听到了一句关于Sass数据验证这块大为感悟&#…...

SQL Server 2025 预览版新功能
T-SQL 语言增强 正则表达式 (Regex) 支持 功能概述: SQL Server 2025 在 T-SQL 中原生引入了 POSIX 兼容的正则表达式支持,通过内置函数(如 REGEXP_LIKE、REGEXP_REPLACE 等)可直接在查询中对文本进行复杂模式匹配、查找和替换。…...
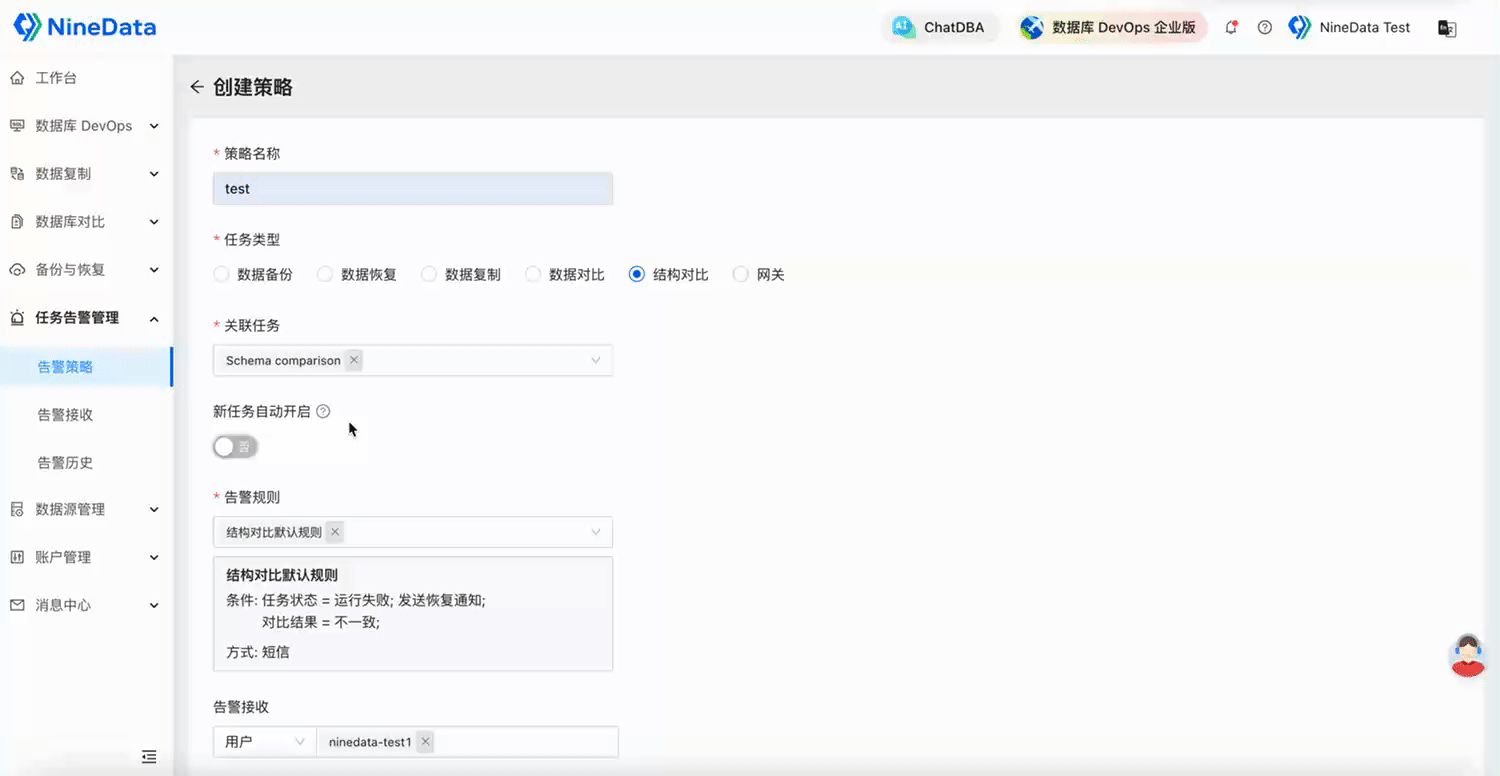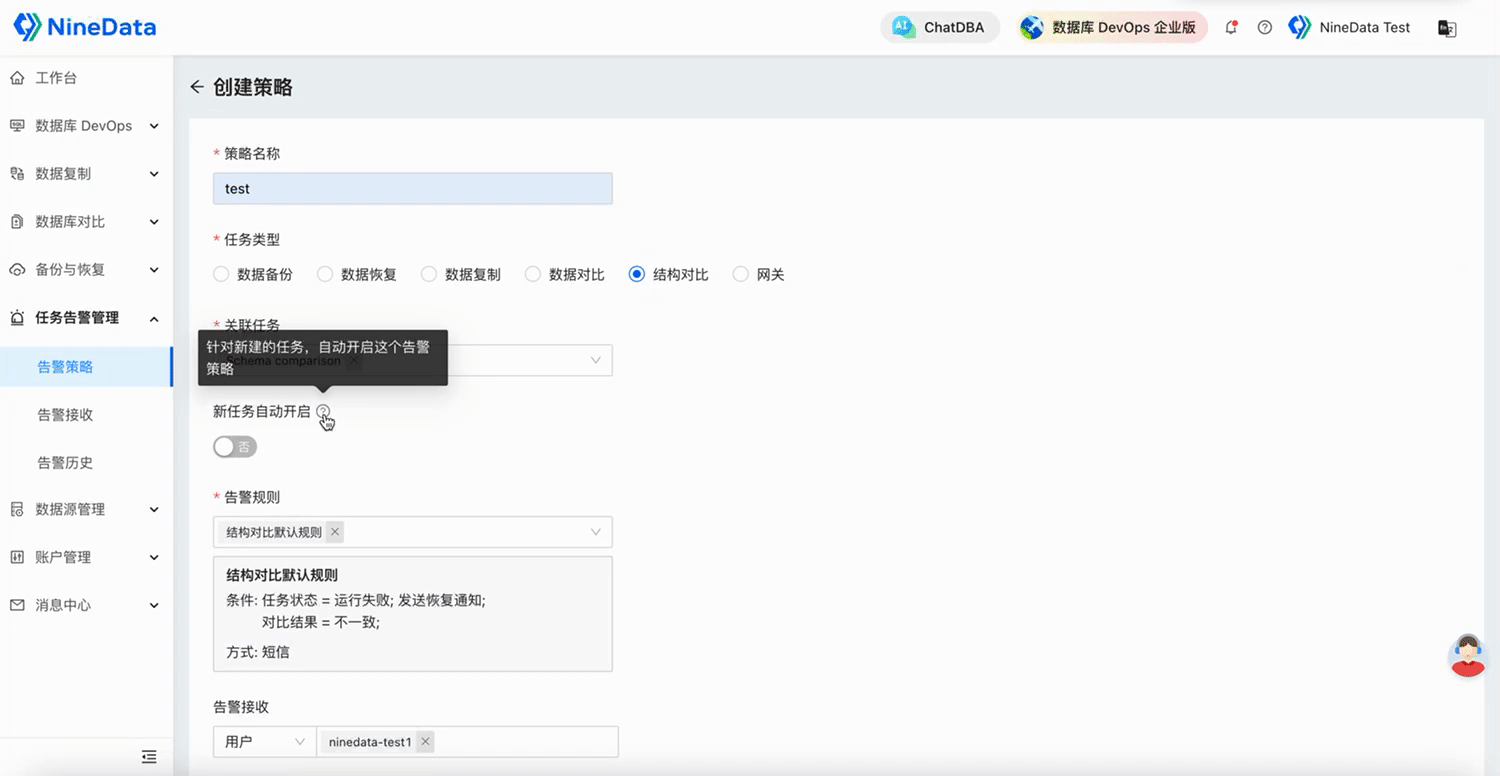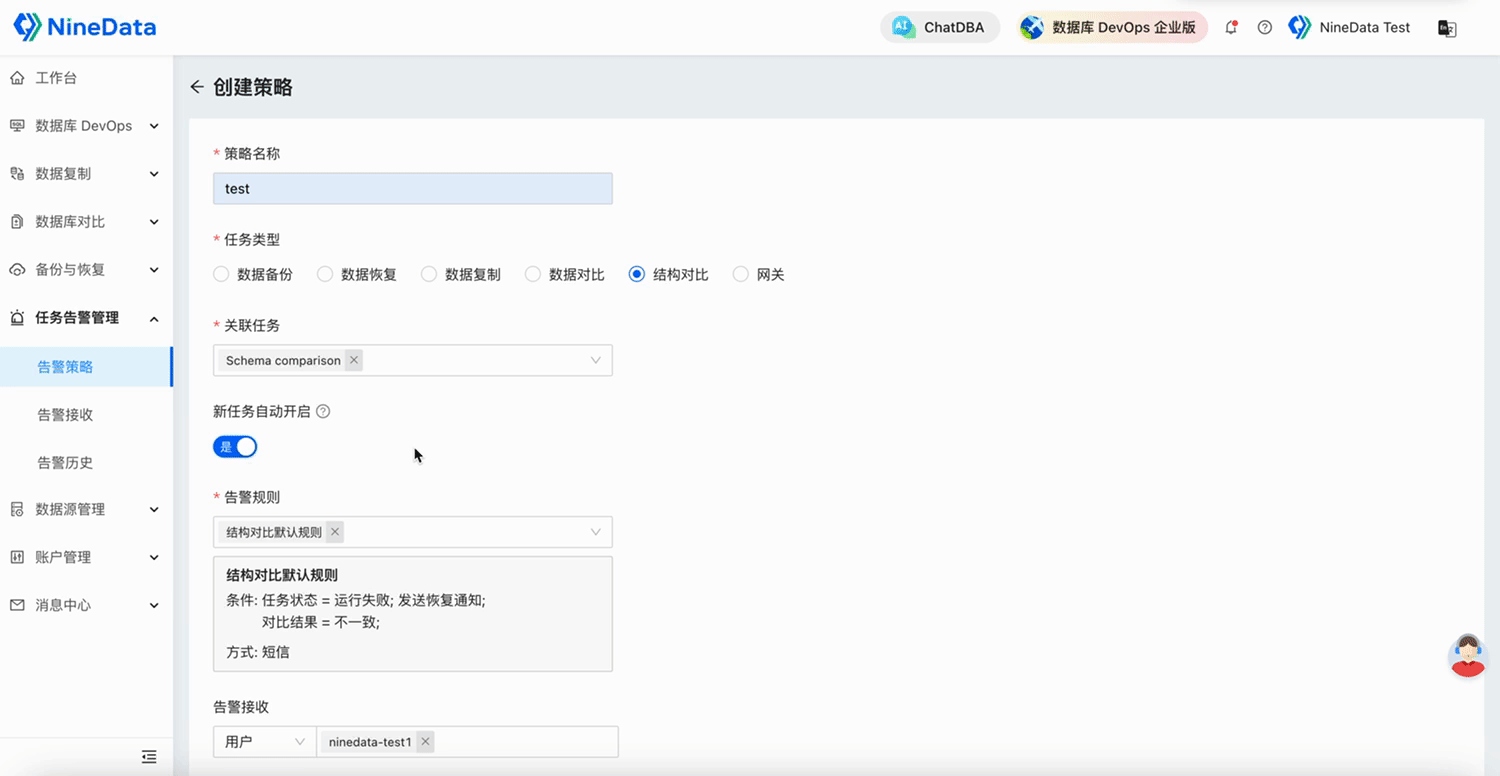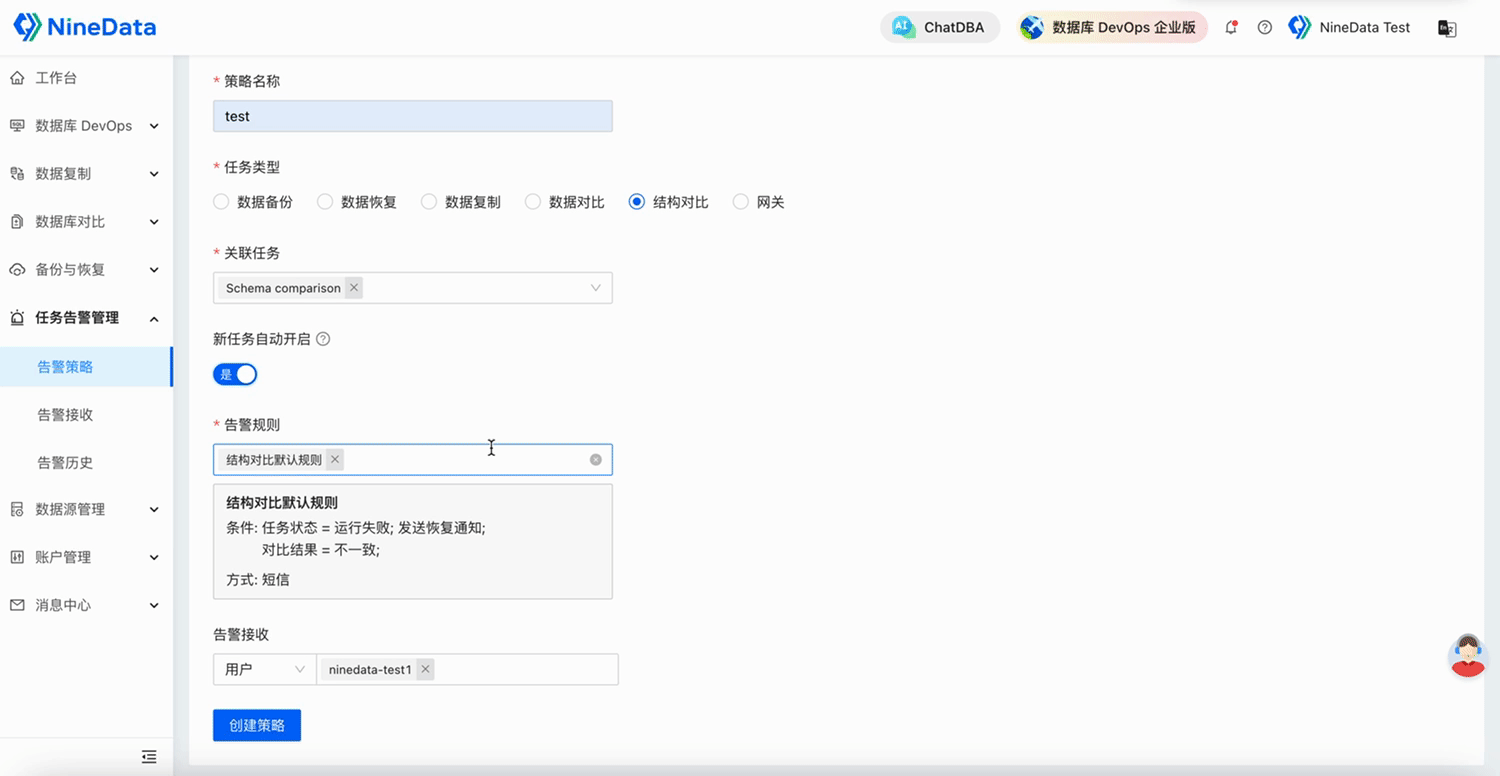
NineData云原生智能数据管理平台新功能发布|2025年5月版
本月发布 6 项更新,其中重点发布 3 项、功能优化 3 项。 重点发布 数据库 DevOps - 多源敏感数据保护 敏感数据扫描能力大幅扩展,新增支持 TiDB、Doris、SelectDB、OceanBase MySQL、GreatSQL、StarRocks、ClickHouse、SingleStore、Lindorm 9 种大数据…...

数学复习笔记 25
今天能把第五章学完。加油。今年是最好上岸的一年。 5.23:全是单根,笑死,居然难受了。我现在每个题,都要总结。总结。总结实际上也总结不出啥东西。但是我一定要总结。主动让自己思考一下。老师的思路很清奇。他认为考的稀松平常…...

Linux可执行文件ELF文件结构
目标文件格式 编译器编译源代码后生成的文件叫做目标文件,而目标文件经过编译器链接之后得到的就是可执行文件。那么目标文件到底是什么?它和可执行文件又有什么区别?链接到底又做了什么呢?接下来,我们将探索一下目标…...

RAG:大模型微调的革命性增强——检索增强生成技术深度解析
RAG:大模型微调的革命性增强——检索增强生成技术深度解析 当大模型遇到知识瓶颈,RAG(检索增强生成)为模型装上"外部记忆库",让静态知识库与动态生成能力完美融合。本文将深入拆解RAG的技术原理、微调策略及…...

DisplayPort 2.0协议介绍(1)
最近开始学习DisplayPort 2.0协议,相比于DP1.4a,最主要的是速率提升到了10Gbps/lane,还有就是128b/132b编码方式的修改。至于速率13.5Gbps和20Gbps还只是可选项,在DP2.1协议才成为必须支持选项。 那在实现技术细节上有哪些变化呢…...

I2C通信讲解
I2C总线发展史 怎么在一条串口线上连接多个设备呢? 由于速度同步线是由主机实时发出的,所以主机可以按需求修改通信速度,这样在一条线上可以挂接不同速度的器件,单片机和性能差的器件通信,就输出较慢的脉冲信号&#x…...
综合知识答案和详解)
【信息系统项目管理师-选择真题】2025上半年(第一批)综合知识答案和详解
更多内容请见: 备考信息系统项目管理师-专栏介绍和目录 文章目录 【第1题】【第2题】【第3题】【第4题】【第5题】【第6题】【第7题】【第8题】【第9题】【第10题】【第11题】【第12题】【第13题】【第14题】【第15题】【第16题】【第17题】【第18题】【第19题】【第20题】【第…...

ABP VNext 在 Kubernetes 中的零停机蓝绿发布
ABP VNext 在 Kubernetes 中的零停机蓝绿发布 🚀 📚 目录 ABP VNext 在 Kubernetes 中的零停机蓝绿发布 🚀📌 一、前提准备 ℹ️🧱 二、项目结构与目标 🎯🐳 三、多阶段 Dockerfile 构建 &#…...

linux 故障处置通用流程-36计-14-27
014:查看系统主要日志 查看以下日志: 主要查以下关键字 error/NIC/fs /"link down"/Oout of memory" /var/log/messages /var/log/dmesg 015:主机通讯是否延迟 执行命令: #ping 网关_IP #ping 关联主机_IP …...

https和http有什么区别-http各个版本有什么区别
http和 https的区别 HTTP(超文本传输协议)和 HTTPS(安全超文本传输协议)是两种用于在网络上传输数据的协议,它们的主要区别在于安全性: HTTP(Hypertext Transfer Protocol)&#x…...

基于回归算法的心理健康预测(EDA + 预测)
心理健康涵盖情感、心理与社会福祉,影响认知、情绪和行为模式,决定压力应对、人际交往及健康决策,且在生命各阶段(从童年至成年)均至关重要。心理健康与身体健康同为整体健康的核心要素:抑郁会增加糖尿病、…...

React Native开发鸿蒙运动健康类应用的项目实践记录
项目名称:HarmonyFitness - 基于React Native的鸿蒙运动健康应用 技术栈:React Native 0.72.5 TypeScript HarmonyOS API ArkTS原生模块 一、环境搭建与项目初始化 双环境配置 React Native环境: npx re…...

【新品解读】一板多能,AXRF49 定义新一代 RFSoC FPGA 开发平台
“硬件系统庞杂、调试周期长” “高频模拟前端不稳定,影响采样精度” “接收和发射链路难以同步,难以扩展更多通道” “数据流量大,处理与存储跟不上” 这些是大部分客户在构建多通道、高频宽的射频采样链路时,面临的主要问题。…...

贪心算法应用:线性规划贪心舍入问题详解
贪心算法应用:线性规划贪心舍入问题详解 贪心算法是一种在每一步选择中都采取当前状态下最优的选择,从而希望导致结果是全局最优的算法策略。在线性规划问题中,贪心算法特别是贪心舍入技术有着广泛的应用。下面我将全面详细地讲解这一主题。…...

YOLO在C#中的完整训练、验证与部署方案
YOLO在C#中的完整训练、验证与部署方案 C# 在 YOLO 部署上优势明显(高性能、易集成),但训练能力较弱,通常需结合 Python 实现。若项目对开发效率要求高且不依赖 C# 生态,建议全程使用 Python;若需深度集成…...
洛谷题目:P2761 软件补丁问题 (本题简单)
个人介绍: 题目传送门: P2761 软件补丁问题 - 洛谷 (luogu.com.cn) 前言: 这道题是一个典型的状态搜索问题,核心目标就是利用给定d额多个补丁程序,将包含若干错误的软件修复成没有错误的状态,并且要使得修复过程当中的总耗时最少。下面是小亦为大家阐述滴思路: 1、状态…...

智慧园区数字孪生全链交付方案:降本增效30%,多案例实践驱动全周期交付
在智慧园区建设浪潮中,数字孪生技术正成为破解传统园区管理难题的核心引擎。通过构建与物理园区1:1映射的数字模型,实现数据集成、状态同步与智能决策,智慧园区数字孪生全链交付方案已在多个项目中验证其降本增效价值——某物流园区通过该方案…...

【OpenGL学习】(四)统一着色和插值着色
文章目录 【OpenGL学习】(四)统一着色和插值着色统一着色(Flat/Uniform Shading)插值着色(Interpolated Shading) 【OpenGL学习】(四)统一着色和插值着色 着色器介绍: h…...

42、响应处理-【源码分析】-浏览器与PostMan内容协商完全适配
42、响应处理源码分析浏览器与PostMan内容协商完全适配 要实现浏览器与PostMan在内容协商上的完全适配,需要在Spring Boot应用中自定义内容协商策略,确保服务器能根据浏览器和PostMan的请求头正确返回合适格式的数据。以下是详细的步骤: ### …...

在 CentOS 上安装 Docker 和 Docker Compose 并配置使用国内镜像源
在 CentOS 上安装 Docker 和 Docker Compose 并配置使用国内镜像源,可以加速镜像下载速度。以下是详细的步骤: 一、安装 Docker 移除旧版本的 Docker(如果有): sudo yum remove docker \docker-client \docker-client…...

Java Lambda表达式深度解析:从入门到实战
简介 Lambda表达式是Java 8引入的最重要特性之一,它极大地简化了Java代码的编写方式,使函数式编程风格在Java中成为可能。本文将全面介绍Lambda表达式的概念、语法、应用场景以及与相关特性的配合使用,帮助开发者掌握这一强大的编程工具。 一、Lambda表达式基础 1.1 什么…...

Docker慢慢学
1、Docker DeskTop 2、N8N下载 docker run -p 8888:5678 n8nio/n8n 3、Kafka kafka依赖zookeeper,先启动zookeeper docker pull zookeeper docker run -d --name zookeeper -p 2181:2181 -e ALLOW_ANONYMOUS_LOGINyes zookeeper 启动kafka docker pull confluentinc/cp…...

cursor-free-vip使用
一、项目简介 Cursor-Free-VIP 是一个开源项目,旨在帮助用户免费使用 Cursor AI 的高级功能。它通过自动注册 Cursor 账号、重置机器 ID 和完成 Auth 验证等操作,解决 Cursor AI 中常见的限制提示。 二、系统准备 1…cursor需要更新到最新的版本 三、…...

使用SSH tunnel访问内网的MySQL
文章目录 环境背景方法参考 注:本文是使用SSH tunnel做端口转发的一个示例。有关SSH端口转发,可参考我的几篇文档 https://blog.csdn.net/duke_ding2/article/details/106878081https://blog.csdn.net/duke_ding2/article/details/135627263https://blo…...

Redis持久化模式RDB与AOF
RDB持久化 RDB也被叫做Redis数据快照。简单来说就是把内存中的所有数据记录到磁盘中。当Redis实例故障重启后重磁盘中读取快照文件进行数据恢复(快照文件默认保存在当前运行目录); 演示Redis正常停机自动执行一次RDB操作 配置Redis触发RDB机制 RDB其它配置也可在red…...

【JS进阶】ES5 实现继承的几种方式
ES5 实现继承的几种方式 1. 原型链继承(Prototype Chaining) function Parent(name) {this.name name || Parent;this.colors [red, blue]; }Parent.prototype.sayName function() {console.log(this.name); };function Child() {}// 关键ÿ…...

【数据结构】树形结构--二叉树(二)
【数据结构】树形结构--二叉树(二) 一.二叉树的实现1.求二叉树结点的个数2.求二叉树叶子结点的个数3.求二叉树第k层结点的个数4.求二叉树的深度(高度)5.在二叉树中查找值为x的结点6.判断二叉树是否为完全二叉树7.二叉树的销毁 一.…...
