【拓扑剪枝+深搜剪枝/计数】2024睿抗-章鱼图的判断
题目描述
对于无向图 G = ( V , E ) G=(V,E) G=(V,E),我们将有且只有一个环的、大于 2 2 2 个顶点的无向连通图称之为章鱼图,因为其形状像是一个环(身体)带着若干个树(触手),故得名。
给定一个无向图,请你判断是不是只有一个章鱼子图存在。
注意:这里的章鱼子图指的是满足章鱼图性质的极大连通子图。
输入格式
输入第一行是一个正整数 T T T,表示数据的组数。
每组数据的第一行是两个正整数 N , M N,M N,M,表示给定的无向图有 N N N 个点, M M M 条边。
接下来的 M M M 行,每行给出一条边两个端点的顶点编号。
注意:顶点编号从 1 1 1 开始,并且题目保证任何边不会重复给出,且没有自环。
输出格式
对于每组数据,如果给定的图里只有一个章鱼子图,则在一行中输出 Yes 和章鱼子图环的大小(及环中顶点数),其间以 1 1 1 个空格分隔。
否则,则在一行中输出 No 和图中章鱼子图的个数,其间以 1 1 1 个空格分隔。
数据范围
1 l e T l e 5 1 \\le T \\le 5 1leTle5,
1 l e N , M l e 10 5 1 \\le N,M \\le 10^5 1leN,Mle105
输入样例:
3
10 10
1 3
3 5
5 7
7 9
1 2
2 4
2 6
3 8
9 10
1 9
10 10
1 3
3 5
5 7
7 9
9 1
1 2
2 4
4 8
8 10
10 1
10 10
1 3
3 5
5 7
7 9
9 1
2 4
4 8
8 10
10 2
10 6
输出样例:
Yes 5
No 0
No 2
拓扑剪枝+深搜剪枝/计数
通过拓扑排序剥离无向图中的非环结构(“触手”),再通过DFS检测并统计剩余环的数量和大小,最终判断图中是否存在单一标准环(所有节点度数为2的连通环)或多个非常规环结构。
C++ 代码
/*
拓扑排序变种:以度数为衡量标准topsort 之效为剥除环之外的树状结构(谓之触手),留环(谓之头部)但须思忖余环呈多环嵌套或多环线连须去除
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10,M = 1e5 + 10;
int h[N],e[2*M],ne[2*M],idx;
int d[N]; // 记录结点度数
int n,m;
int cnt,ans;// 加边
void add(int a, int b){e[idx]=b;ne[idx]=h[a];h[a]=idx++;
}void topsort(){// 初始化队列queue<int> q;// 度0/1入队for(int i=1;i<=n;i++){if(d[i] == 1) q.push(i);}// 取队首,(归序),削邻度// 度0/1入,周而复始,队空则成while(!q.empty()){int t=q.front();q.pop();// 度数要变化!!d[t]--;for(int i=h[t]; ~i ; i = ne[i]){int j=e[i];if(--d[j] == 1) q.push(j);}}
}// 清除环并且记录环结点数
void dfs(int u){cnt ++;d[u]=0; // 清空当前节点的度数for(int i=h[u];~i;i=ne[i]){if(d[e[i]]) dfs(e[i]);}
}void solve(){cin>>n>>m;// 清空 idx,h,didx = 0;memset(h,-1,sizeof h);memset(d,0,sizeof d);// 初始化while(m--){int x,y;cin>>x>>y;add(x,y);add(y,x);d[x]++;d[y]++; // 度数加1}// topsort去除所有的非环topsort();// 去除所有的特异环for(int i=1;i<=n;i++){if(d[i]>0 && d[i]!=2){dfs(i);}}ans=cnt=0;for(int i=1;i<=n;i++){if(d[i] == 2){dfs(i);ans++;}}if(ans == 1){cout << "Yes" << " " << cnt << endl;}else{cout << "No" << " " << ans << endl;}
}int main(){int T;cin>>T;while(T--){solve();}return 0;
}
相关文章:

【拓扑剪枝+深搜剪枝/计数】2024睿抗-章鱼图的判断
题目描述 对于无向图 G ( V , E ) G(V,E) G(V,E),我们将有且只有一个环的、大于 2 2 2 个顶点的无向连通图称之为章鱼图,因为其形状像是一个环(身体)带着若干个树(触手),故得名。 给定一个…...

Android基础回顾】六:安卓显示机制Surface 、 SurfaceFlinger、Choreographer
在 Android 系统中,Surface 和 SurfaceFlinger 是图形渲染系统的核心组件,负责屏幕显示内容的合成与管理。它们协同工作,使各种 App 和系统界面能够高效地显示在屏幕上。 1 Surface 是什么? Surface 是一个抽象的图形缓冲区接口…...

SpringBoot核心注解详解及3.0与2.0版本深度对比
SpringBoot核心注解详解及3.0与2.0版本深度对比 本文全面解析SpringBoot核心注解原理,深入对比3.0与2.0版本差异,助你掌握新一代SpringBoot开发精髓 一、SpringBoot核心注解全景解析 1.1 什么是SpringBoot核心注解 SpringBoot核心注解是构建SpringBoot…...

敏捷开发中如何避免过度加班
在敏捷开发过程中避免过度加班,需要明确敏捷原则、合理规划迭代任务、加强团队沟通、优化流程效率、设定合理的工作负荷、注重团队士气和成员健康。明确敏捷原则,即保证可持续发展的步调,避免频繁地变更需求、过度承诺任务量。合理规划迭代任…...

深入浅出多路归并:原理、实现与实战案例解析
文章目录 二路归并多路归并方法一:指针遍历(多指针比较法)方法二:小根堆法(最小堆归并) 实际场景外部排序 经典题目丑数Ⅱ方法一:三指针法方法二:优先队列法(K路归并&…...

Java八股文——集合「Map篇」
Map 面试官您好,关于 Java 中常见的 Map 集合,我可以从非线程安全和线程安全两个方面来介绍: 首先,我们来看一下非线程安全的 Map 实现,这些在单线程环境下性能通常更好,但在并发场景下需要外部同步&…...

第1章_数据分析认知_知识点笔记
来自:数据分析自学课程-戴戴戴师兄 逐字稿:【课程4.0】第1章_分析认知_知识点笔记 【课程4.0】第1章 分析认知 知识点总结 数据分析的核心价值不是工具,而是用数据驱动业务增长。 一、数据分析的本质认知 数据分析是什么? 不是酷…...

111页可编辑精品PPT | 华为业务变革框架及战略级项目管理华为变革管理华为企业变革华为的管理模式案例培训
这份文档是关于华为公司业务变革管理框架(BTMS)V2.0的详细介绍,涵盖从年度规划到项目执行的全流程管理。BTMS框架通过变革战略规划、年度规划流程、解决方案开发(PMOP流程)、运作管理流程等多个模块,系统地…...

Python使用总结之Mac安装docker并配置wechaty
Python使用总结之Mac安装docker并配置wechaty ✅ 一、安装 Docker Desktop for macOS 1. 下载 Docker Desktop 安装包 访问官网下载安装包: 👉 https://www.docker.com/products/docker-desktop 选择 macOS (Apple 芯片或 Intel 芯片) 版本下载。 …...
html文字红色粗体,闪烁渐变动画效果
1. 代码 <!DOCTYPE html> <html lang"zh"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>红色粗体闪烁文字表格</title><s…...

进阶配置与优化:配置 HTTPS 以确保数据安全传输
在生产环境中,确保用户与服务器之间的数据传输安全至关重要。配置 HTTPS(HTTP Secure)可以通过使用 SSL/TLS 协议对数据进行加密,防止数据在传输过程中被窃听或篡改。本文将详细介绍如何使用 Let’s Encrypt 免费获取 SSL 证书&am…...

Python使用clickhouse-local和MySQL表函数实现从MySQL到ClickHouse数据同步
下面是一个使用clickhouse-local和MySQL表函数实现从MySQL到ClickHouse数据同步的Python解决方案,包含全量同步、增量同步和测试用例。 此解决方案提供了生产级数据同步所需的核心功能,可根据具体场景扩展更多高级特性如:数据转换、字段映射…...

解锁Java线程池:性能优化的关键
一、引言 在 Java 并发编程的世界里,线程池是一个至关重要的概念。简单来说,线程池就是一个可以复用线程的 “池子”,它维护着一组线程,这些线程可以被重复使用来执行多个任务,而不是为每个任务都创建一个新的线程。…...

如何自定义一个 Spring Boot Starter?
导语: 在后端 Java 面试中,Spring Boot 是绕不开的重点,而“如何自定义一个 Starter”作为进阶开发能力的体现,常被面试官用于考察候选人的工程架构思维与 Spring Boot 底层掌握程度。本文将带你深入理解自定义 Starter 的实现逻辑…...
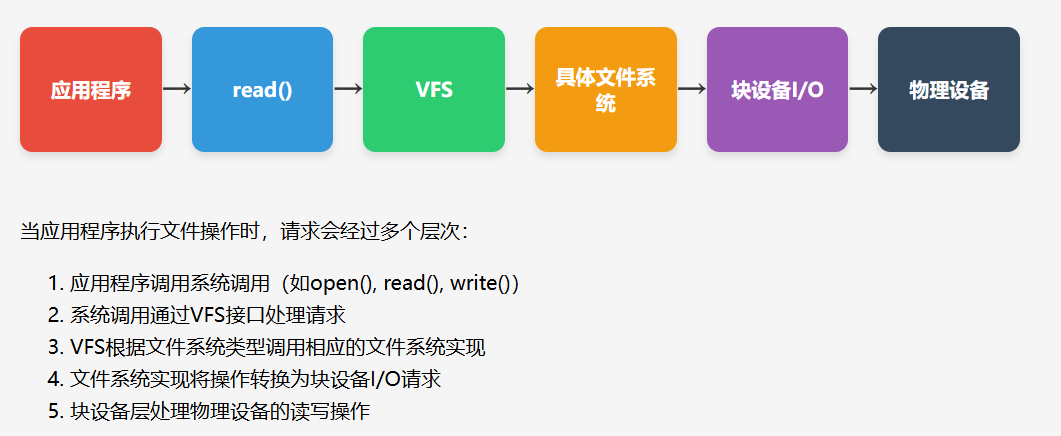
Linux文件系统详解:从入门到精通
无论是开发高性能应用还是进行系统级编程,文件系统都是我们必须掌握的基础知识。今天,我将带大家深入浅出地了解Linux文件系统的核心概念和工作原理。 一、Linux文件系统概述 Linux文件系统是操作系统中负责管理持久存储设备上数据的子系统。它不仅仅是…...

Electron Fiddle使用笔记
文章目录 下载界面示意图保存和打开项目save 和 save as forge project 其他文档打包报错 RequestError: read ECONNRESET 想要打包前端程序,奈何本地环境总是报错,意外发现可以通过electron fiddle直接调试代码。 下载 百度网盘地址: 首次…...
)
【PhysUnits】16.1 完善Var 结构体及其运算(variable.rs)
一、源码 这段代码定义了一个泛型结构体 Var,并为它实现了各种数学运算。 /** 变量结构体 Var* 该结构体泛型参数 T 需满足 Numeric 约束*/use core::ops::{Neg, Add, Sub, Mul}; use crate::constant::Integer; /// 定义 Numeric trait,约束 T 必须实…...

企业培训学习考试系统源码 ThinkPHP框架+Uniapp支持多终端适配部署
在数字化转型浪潮下,企业对高效培训与精准考核的需求日益迫切。一套功能完备、多终端适配且易于定制的培训学习考试系统,成为企业提升员工能力、检验培训成果的关键工具。本文给大家分享一款基于 ThinkPHP 框架与 Uniapp 开发的企业培训学习考试系统&…...

C++ if语句完全指南:从基础到工程实践
一、选择结构在程序设计中的核心地位 程序流程控制如同城市交通网络,if语句则是这个网络中的决策枢纽。根据ISO C标准,选择结构占典型项目代码量的32%-47%,其正确使用直接影响程序的: 逻辑正确性 执行效率 可维护性 安全边界 …...

SpringBoot手动实现流式输出方案整理以及SSE规范输出详解
背景: 最近做流式输出时,一直使用python实现的,应需求方的要求,需要通过java应用做一次封装并在java侧完成系统鉴权、模型鉴权等功能后才能真正去调用智能体应用,基于此调研java实现流式输出的几种方式,并…...

深入解析I²C总线接口:从基础到应用
IC总线概述与基本概念 一句话概述:本章节将介绍IC总线的历史、定义及其在嵌入式系统中的作用,帮助读者建立对IC的基本理解。 IC(Inter-Integrated Circuit)总线是一种广泛应用于嵌入式系统中的串行通信协议,最初由飞利…...

Sklearn 机器学习 缺失值处理 检测数据每列的缺失值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在代码与灵感交织的数字世界里和大家相遇~💖 ✨ 在这个技术浪潮奔涌的时代,我们既是探索者,也是分享者。我始终相信,每一行代码都是通往创新的钥匙,而分享则能让这把钥匙照亮更多人的…...

Unity基于GraphView的可视化关卡编辑器开发指南
一、GraphView技术基础与应用场景 1. GraphView核心组件 组件功能描述关卡编辑应用GraphView画布容器关卡拓扑结构编辑区Node基础节点房间/敌人/道具等关卡元素Edge节点连接线路径/依赖关系Port连接端口入口/出口标记Blackboard属性面板元素参数配置Minimap缩略图导航大型关卡…...

STL解析——list的使用
目录 1.简介 2.构造函数 3.迭代器 3.1封装 3.2迭代器分类 4.排序性能 4.1链式与数组 4.2缓存读取 1.简介 STL容器中提供的list容器也是一种顺序容器,底层实现方式是带头双向链表,这种实现方式能比单链表更高效的访问数据。 下面围绕部分重要接口…...

华为大规模——重塑生产力
华为大模型通过以下几个方面重塑生产力: 提供强大算力支持 华为致力于构建领先的昇腾人工智能算力平台,推出高性能昇腾AI集群,支持月级长期稳定训练,可靠性业界领先。同时打造开放的昇腾计算平台,兼容主流算子、框…...

【Go面试陷阱】对未初始化的chan进行读写为何会卡死?
Go面试陷阱:对未初始化的chan进行读写为何会卡死?深入解析nil channel的诡异行为 在Go的世界里,var ch chan int 看似人畜无害,实则暗藏杀机。它不会报错,不会panic,却能让你的程序悄无声息地"卡死&qu…...

SpringBoot自动化部署实战技术文章大纲
技术背景与目标 介绍SpringBoot在现代开发中的重要性自动化部署的价值:提升效率、减少人为错误、实现CI/CD适用场景:中小型Web应用、微服务架构 自动化部署核心方案 基于Docker的容器化部署 SpringBoot应用打包为Docker镜像使用Docker Compose编排多容…...
 软件项目任务分解)
软件项目管理(3) 软件项目任务分解
一、相关概念 1.任务分解的方法和步骤 (1)方法 模板参照方法:参照有标准或半标准的任分解结构图类比方法:任务分解结构图经常被重复使用,具有相似性自顶向下方法:一般->特殊,演绎推理从大…...

MQTTX连接阿里云的物联网配置
本文的目标是通过MQTTX的客户端,连接到阿里云的物联网的平台,发送温度信息,在阿里云的平台中显示出来。阿里云免费注册,免费有一个MQTT的服务器。有数量限制,但是对于测试来讲,已经足够。 1、注册阿里云的物…...

20250606-C#知识:匿名函数、Lambda表达式与闭包
C#知识:匿名方法、Lambda表达式与闭包 闭包乍一听感觉很复杂,其实一点也不简单 1、匿名方法 没有方法名的方法一般用于委托和事件 Func<int, int, int> myAction delegate(int a, int b) { return a b; }; Console.WriteLine( myAction(1, 2)…...
