机器学习:支持向量机(SVM)原理解析及垃圾邮件过滤实战
一、什么是支持向量机(SVM)
1. 基本概念
1.1 二分类问题的本质
在机器学习中,分类问题是最常见的任务之一。最简单的情况就是二分类:比如一封邮件是“垃圾邮件”还是“正常邮件”?一个病人是“患病”还是“健康”?一个图像是“猫”还是“狗”?
SVM专门擅长处理这种“把样本分成两类”的问题。它的核心目标是:找到一个最优的边界,把两类样本尽可能清晰地分开。
1.2 最大间隔划分思想
SVM的最大特点,就是它不像KNN那样靠近邻,也不像逻辑回归那样直接拟合概率,而是追求“最大间隔”:
它试图在两个类别之间,找到一条“超平面”(一个直线、一个面、或者一个高维空间中的超平面),这个超平面与两类样本中最近的点之间的距离最大,这个“最近的点”就是“支持向量”。
为什么要最大化这个间隔?
简单来说:更大的间隔 = 更强的容错率 = 更好的泛化能力。
1.3 支持向量的意义
在SVM中,真正决定这个“最佳分隔线”的,并不是所有数据点,而是最接近这条线的一小部分点,我们称之为“支持向量”。
这些支持向量对模型训练有决定性作用,一旦它们的位置改变,分界线就可能会改变。而其他点的影响几乎为零。
2. 超平面与间隔
-
超平面:在二维中是直线,在三维中是平面,在更高维中是“超平面”。SVM的目标就是找到这样一个能分开两类样本的超平面。
-
间隔:超平面到支持向量的最小距离。SVM通过最大化这个间隔来优化模型。
这是一种几何直觉非常强的优化方式,适合处理线性可分的数据。
2.1 硬间隔
**硬间隔(Hard Margin)**是支持向量机(SVM)中的一个概念,指的是在分类过程中,模型要求训练数据必须被完全正确分类,且每个样本点都不能落在分类间隔区域内。
直白解释:
硬间隔就是:“我要找到一条完美的分界线,一个样本都不能错分,也不能碰到分界线附近的空白区域。”
2.1.1 硬间隔的定义
设训练数据集为:
{ ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x n , y n ) } , x i ∈ R d , y i ∈ { − 1 , + 1 } \{(x_1, y_1), (x_2, y_2), \dots, (x_n, y_n)\},\quad x_i \in \mathbb{R}^d,\quad y_i \in \{-1, +1\} {(x1,y1),(x2,y2),…,(xn,yn)},xi∈Rd,yi∈{−1,+1}
SVM 要求找到一个线性可分的超平面:
w T x + b = 0 w^T x + b = 0 wTx+b=0
使得所有训练样本被完全正确分类,并且分类间隔最大。
约束条件(分类正确 + 间隔大):
对所有样本 i = 1 , 2 , . . . , n i = 1, 2, ..., n i=1,2,...,n,要求:
y i ( w T x i + b ) ≥ 1 y_i (w^T x_i + b) \geq 1 yi(wTxi+b)≥1
这表示:
-
如果 y i = + 1 y_i = +1 yi=+1,则 w T x i + b ≥ 1 w^T x_i + b \geq 1 wTxi+b≥1
-
如果 y i = − 1 y_i = -1 yi=−1,则 w T x i + b ≤ − 1 w^T x_i + b \leq -1 wTxi+b≤−1
也就是说:每个样本都要落在自己那一侧的“边界外”,而且不能在间隔区域里、也不能分类错误。
优化目标(最大间隔 = 最小化 ∥ w ∥ 2 \|w\|^2 ∥w∥2):
支持向量机通过最大化间隔来实现最优划分。因为几何间隔是 2 ∥ w ∥ \frac{2}{\|w\|} ∥w∥2,最大化它等价于最小化 ∥ w ∥ 2 \|w\|^2 ∥w∥2。
所以硬间隔 SVM 的优化问题是:
min w , b 1 2 ∥ w ∥ 2 subject to y i ( w T x i + b ) ≥ 1 , ∀ i = 1 , . . . , n \begin{aligned} \min_{w, b} \quad & \frac{1}{2} \|w\|^2 \\ \text{subject to} \quad & y_i (w^T x_i + b) \geq 1,\quad \forall i = 1, ..., n \end{aligned} w,bminsubject to21∥w∥2yi(wTxi+b)≥1,∀i=1,...,n
硬间隔只适用于:
-
数据完全线性可分
-
没有噪声和异常值
如果你的数据本身是完全线性可分的,比如下图中的两类点完全不重叠,那么硬间隔SVM就可以很完美地找到一个“最大间隔的超平面”来分开它们。

一旦数据中有噪声或重叠样本,硬间隔就无法找到合理解,甚至根本无法收敛。这时我们就要用软间隔,允许一些“点分类错了”,换取更强的容错能力。
2.1.2 硬间隔的对偶问题
构造拉格朗日函数(Lagrangian)
引入拉格朗日乘子 α i ≥ 0 \alpha_i \geq 0 αi≥0,对应约束 y i ( w T x i + b ) ≥ 1 y_i(w^T x_i + b) \geq 1 yi(wTxi+b)≥1。
构造拉格朗日函数:
L ( w , b , α ) = 1 2 ∥ w ∥ 2 − ∑ i = 1 n α i [ y i ( w T x i + b ) − 1 ] \mathcal{L}(w, b, \alpha) = \frac{1}{2} \|w\|^2 - \sum_{i=1}^n \alpha_i [y_i(w^T x_i + b) - 1] L(w,b,α)=21∥w∥2−i=1∑nαi[yi(wTxi+b)−1]
对偶问题推导步骤
我们要最小化 L \mathcal{L} L 关于 w w w 和 b b b,最大化关于 α \alpha α。
先求偏导设置为 0:
1. 对 w w w 求导并令其为 0:
∂ L ∂ w = w − ∑ i = 1 n α i y i x i = 0 ⇒ w = ∑ i = 1 n α i y i x i \frac{\partial \mathcal{L}}{\partial w} = w - \sum_{i=1}^n \alpha_i y_i x_i = 0 \Rightarrow w = \sum_{i=1}^n \alpha_i y_i x_i ∂w∂L=w−i=1∑nαiyixi=0⇒w=i=1∑nαiyixi
2. 对 b b b 求导并令其为 0:
∂ L ∂ b = − ∑ i = 1 n α i y i = 0 ⇒ ∑ i = 1 n α i y i = 0 \frac{\partial \mathcal{L}}{\partial b} = - \sum_{i=1}^n \alpha_i y_i = 0 \Rightarrow \sum_{i=1}^n \alpha_i y_i = 0 ∂b∂L=−i=1∑nαiyi=0⇒i=1∑nαiyi=0
代入得对偶问题
将 w w w 表达式代入 L \mathcal{L} L,得到只关于 α \alpha α 的对偶问题:
max α ∑ i = 1 n α i − 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j x i T x j s.t. ∑ i = 1 n α i y i = 0 α i ≥ 0 , ∀ i \begin{aligned} \max_{\alpha} \quad & \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j y_i y_j x_i^T x_j \\ \text{s.t.} \quad & \sum_{i=1}^n \alpha_i y_i = 0 \\ & \alpha_i \geq 0,\quad \forall i \end{aligned} αmaxs.t.i=1∑nαi−21i=1∑nj=1∑nαiαjyiyjxiTxji=1∑nαiyi=0αi≥0,∀i
这就是 硬间隔 SVM 的对偶形式。
它是一个凸二次规划问题,可以用标准优化算法求解。
2.2 软间隔
软间隔(Soft Margin)是支持向量机(SVM)在面对现实中不可完美划分数据时,引入的一种“宽容机制”。
通俗来说:
如果“硬间隔”是一个完美主义者,要求训练集所有点都正确分类;
那么“软间隔”就是个现实主义者,承认一些点可能分类错误,但整体效果更重要。
现实中的数据常常:
-
有噪声(例如标注错误、输入异常);
-
两类样本有重叠;
-
完全线性可分几乎不可能。
此时,如果继续使用硬间隔 SVM,会导致:
-
模型无法收敛;
-
过拟合噪声点,泛化能力差。
所以我们需要“放松限制”——允许一部分样本距离边界近,甚至被分错,但整体间隔仍尽可能大。
2.2.1 软间隔的形式定义
引入松弛变量 ξ i ≥ 0 \xi_i \geq 0 ξi≥0 来表示第 i i i 个样本允许“违背间隔要求”的程度。
优化问题变成:
min w , b , ξ 1 2 ∥ w ∥ 2 + C ∑ i = 1 n ξ i subject to y i ( w T x i + b ) ≥ 1 − ξ i , ∀ i ξ i ≥ 0 , ∀ i \begin{aligned} \min_{w, b, \xi} \quad & \frac{1}{2} \|w\|^2 + C \sum_{i=1}^{n} \xi_i \\ \text{subject to} \quad & y_i (w^T x_i + b) \geq 1 - \xi_i,\quad \forall i \\ & \xi_i \geq 0,\quad \forall i \end{aligned} w,b,ξminsubject to21∥w∥2+Ci=1∑nξiyi(wTxi+b)≥1−ξi,∀iξi≥0,∀i
解释各个部分含义:
- 1 2 ∥ w ∥ 2 \frac{1}{2} \|w\|^2 21∥w∥2:仍然是“最大化间隔”的目标;
- ξ i \xi_i ξi:表示第 i i i 个样本有多“违反”分类边界;
* ξ i = 0 \xi_i = 0 ξi=0:正常分类、在间隔外;
* 0 < ξ i < 1 0 < \xi_i < 1 0<ξi<1:在间隔边界内但没错分;
* ξ i > 1 \xi_i > 1 ξi>1:被分错类;- C C C:是一个超参数,控制“间隔最大化”与“容忍错误”的权衡:
* C 大:更偏向少错分(严格)→ 更可能过拟合;
* C 小:更偏向宽容误差(松弛)→ 更强泛化能力。
2.2.2 软间隔的对偶问题
构造拉格朗日函数
引入拉格朗日乘子:
-
α i ≥ 0 \alpha_i \geq 0 αi≥0:对应约束 y i ( w T x i + b ) ≥ 1 − ξ i y_i(w^T x_i + b) \geq 1 - \xi_i yi(wTxi+b)≥1−ξi
-
μ i ≥ 0 \mu_i \geq 0 μi≥0:对应约束 ξ i ≥ 0 \xi_i \geq 0 ξi≥0
拉格朗日函数为:

对偶问题推导(KKT 条件)
我们将对 w , b , ξ w, b, \xi w,b,ξ 求偏导并设为 0:
对 w w w 求导:
∂ L ∂ w = w − ∑ i = 1 n α i y i x i = 0 ⇒ w = ∑ i = 1 n α i y i x i \frac{\partial \mathcal{L}}{\partial w} = w - \sum_{i=1}^n \alpha_i y_i x_i = 0 \Rightarrow w = \sum_{i=1}^n \alpha_i y_i x_i ∂w∂L=w−i=1∑nαiyixi=0⇒w=i=1∑nαiyixi
对 b b b 求导:
∂ L ∂ b = − ∑ i = 1 n α i y i = 0 ⇒ ∑ i = 1 n α i y i = 0 \frac{\partial \mathcal{L}}{\partial b} = -\sum_{i=1}^n \alpha_i y_i = 0 \Rightarrow \sum_{i=1}^n \alpha_i y_i = 0 ∂b∂L=−i=1∑nαiyi=0⇒i=1∑nαiyi=0
对 ξ i \xi_i ξi 求导:
∂ L ∂ ξ i = C − α i − μ i = 0 ⇒ α i ≤ C ( 因为 μ i ≥ 0 ) \frac{\partial \mathcal{L}}{\partial \xi_i} = C - \alpha_i - \mu_i = 0 \Rightarrow \alpha_i \leq C \quad (\text{因为 } \mu_i \geq 0) ∂ξi∂L=C−αi−μi=0⇒αi≤C(因为 μi≥0)
最终对偶问题形式
整理后,软间隔 SVM 的对偶问题为:
max α ∑ i = 1 n α i − 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j x i T x j s.t. ∑ i = 1 n α i y i = 0 0 ≤ α i ≤ C , ∀ i \begin{aligned} \max_{\alpha} \quad & \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j y_i y_j x_i^T x_j \\ \text{s.t.} \quad & \sum_{i=1}^n \alpha_i y_i = 0 \\ & 0 \leq \alpha_i \leq C,\quad \forall i \end{aligned} αmaxs.t.i=1∑nαi−21i=1∑nj=1∑nαiαjyiyjxiTxji=1∑nαiyi=00≤αi≤C,∀i
相比于硬间隔的对偶问题,这里:
-
增加了上界 α i ≤ C \alpha_i \leq C αi≤C,体现对误差的容忍;
-
因此更适合实际带噪音的数据;
-
仍然是一个凸二次规划问题。
3. 核函数
3.1 核函数的定义
支持向量机算法分类和回归方法的中都支持线性性和非线性类型的数据类型。非线性类型通常是二维平面不可分,为了使数据可分,需要通过一个函数将原始数据映射到高维空间,从而使得数据在高维空间很容易可分,需要通过一个函数将原始数据映射到高维空间,从而使得数据在高维空间很容易区分,这样就达到数据分类或回归的目的,而实现这一目标的函数称为核函数。


3.2 常见的核函数
1. 线性核(Linear Kernel)
K ( x , x ′ ) = x T x ′ K(x, x') = x^T x' K(x,x′)=xTx′
适用场景:
-
特征数非常大(如文本分类)
-
数据本身已经线性可分或接近线性
2. 多项式核
K ( x , x ′ ) = ( x T x ′ + c ) d K(x, x') = (x^T x' + c)^d K(x,x′)=(xTx′+c)d
其中 d d d:多项式的次数, c c c:常数项(通常 c ≥ 0 c \geq 0 c≥0)
适用场景:
-
特征间有高阶交互关系的情况
-
对非线性边界较敏感的问题
3. 高斯核
K ( x , x ′ ) = exp ( − ∥ x − x ′ ∥ 2 2 σ 2 ) K(x, x') = \exp\left(-\frac{\|x - x'\|^2}{2 \sigma^2} \right) K(x,x′)=exp(−2σ2∥x−x′∥2)
其中 σ \sigma σ:控制“邻近范围”的宽度(或使用 γ = 1 2 σ 2 \gamma = \frac{1}{2\sigma^2} γ=2σ21)
适用场景:
-
不知道数据的具体分布情况
-
默认首选的非线性核
4. Sigmoid 核(双曲正切核)
K ( x , x ′ ) = tanh ( κ x T x ′ + c ) K(x, x') = \tanh(\kappa x^T x' + c) K(x,x′)=tanh(κxTx′+c)
类似于神经元中的激活函数
适用场景:
-
模拟神经网络的效果(如早期神经 SVM 研究)
-
情况较少使用
二、代码实战
1. 实验内容
实战要求:使用SVM建立自己的垃圾邮件过滤器。首先需要将每个邮件x变成一个n维的特征向量,并训练一个分类器来分类给定的电子邮件x是否属于垃圾邮件 ( y = 1 ) (y=1)(y=1) 或者非垃圾邮件 ( y = 0 ) (y=0)(y=0) 。
已有数据集:emailSample1.txt, vocab.txt, spamTrain.mat, spamTest.mat
2.代码实现
1. 加载并查看样例邮件内容
#查看样例邮件
f = open('emailSample1.txt', 'r').read()
print(f)
读取一封样例邮件的原始文本内容,便于后续处理。
2. 邮件预处理函数 processEmail
def processEmail(email):email = email.lower() #转化为小写email = re.sub('<[^<>]+>', ' ', email) #移除所有HTML标签email = re.sub(r'(http|https)://[^\s]*', 'httpaddr', email) #将所有的URL替换为'httpaddr'email = re.sub(r'[^\s]+@[^\s]+', 'emailaddr', email) #将所有的地址替换为'emailaddr'email = re.sub(r'\d+', 'number', email) #将所有数字替换为'number'email = re.sub('[$]+', 'dollar', email) #将所有美元符号($)替换为'dollar'#将所有单词还原为词根//移除所有非文字类型,空格调整stemmer = nltk.stem.PorterStemmer() #使用Porter算法tokens = re.split(r'[ @$/#.-:&*+=\[\]?!()\{\},\'\">_<;%]', email) #把邮件分割成单个的字符串,[]里面为各种分隔符tokenlist = []for token in tokens:token = re.sub('[^a-zA-Z0-9]', '', token) #去掉任何非字母数字字符try: #porterStemmer有时会出现问题,因此用trytoken = stemmer.stem(token) #词根except:token = ''if len(token) < 1: continue #字符串长度小于1的不添加到tokenlist里tokenlist.append(token)return tokenlist
核心步骤解释:
-
统一格式:转小写、去 HTML 标签、替换网址、邮箱、数字、货币符号等。
-
分词:使用正则表达式切分文本成单词。
-
词干提取(stemming):调用 NLTK 的 PorterStemmer,还原单词基本形式,如 running → run。
-
清洗:剔除空词、特殊符号,返回标准词汇列表。
- 词汇表映射及向量化处理
vocab_list = np.loadtxt('vocab.txt', dtype='str', usecols=1)
词汇表 vocab.txt 中存有 1899 个关键词。
下面两个函数实现了“文本 → 向量”转换:
def word_indices(processed_f, vocab_list):indices = []for i in range(len(processed_f)):for j in range(len(vocab_list)):if processed_f[i]!=vocab_list[j]:continueindices.append(j+1)return indices
def emailFeatures(indices):features = np.zeros((1899))for each in indices:features[each-1] = 1 #若indices在对应单词表的位置上词语存在则记为1return features
效果:
每封邮件被表示成一个 1899维的二进制特征向量,其中:
-
第 i i i 个位置为
1,表示邮件中包含词汇表中第 i i i 个词。 -
类似 One-hot 编码,但是多热(multi-hot)表示。
- 训练 SVM 模型
train = scio.loadmat('spamTrain.mat')
train_x = train['X']
train_y = train['y']
- 载入 .mat 格式的训练数据。
- X 为 4000 封邮件的特征矩阵,y 为对应的垃圾与非垃圾标签(1 或 0)。
clf = svm.SVC(C=0.1, kernel='linear')
clf.fit(train_x, train_y)
- 使用线性核训练 SVM 模型。
- 参数 C=0.1 控制软间隔的惩罚程度,越小越宽容。
- 模型评估
def accuracy(clf, x, y):predict_y = clf.predict(x)m = y.sizecount = 0for i in range(m):count = count + np.abs(int(predict_y[i])-int(y[i])) #避免溢出错误得到225return 1-float(count/m)
- 自定义精度计算函数,统计预测正确率。
train_accuracy = accuracy(clf, train_x, train_y)
test_accuracy = accuracy(clf, test['Xtest'], test['ytest'])
- 解释模型——重要单词排序
print(vocab_list[np.argsort(clf.coef_).flatten()[i]], end=' ')
- SVM 的线性模型可以通过系数权重判断哪些词对“判定为垃圾邮件”影响最大。
打印前 15 个正权重最大词汇,说明:
邮件中若含这些词,更可能是垃圾邮件。
- 预测新邮件是否为垃圾邮件
t = open('spamSample2.txt', 'r').read()
processed_f = processEmail(t)
f_indices = word_indices(processed_f, vocab_list)
x = np.reshape(emailFeatures(f_indices), (1,1899))
clf.predict(x)
- 流程和训练集一致,对新邮件样本做预处理 → 向量化 → 调用模型预测。
- 输出为 1(垃圾)或 0(正常)。
- PCA 可视化 SVM 决策边界
# PCA降维到2维
pca = PCA(n_components=2)
train_x_pca = pca.fit_transform(train_x)# 重新训练一个2维的SVM,用于绘制决策边界
clf_pca = svm.SVC(C=0.1, kernel='linear')
clf_pca.fit(train_x_pca, train_y)# 画图
plt.figure(figsize=(10, 6))# 绘制不同类别样本点
plt.scatter(train_x_pca[train_y==0, 0], train_x_pca[train_y==0, 1], c='blue', label='Non-spam', edgecolors='k')
plt.scatter(train_x_pca[train_y==1, 0], train_x_pca[train_y==1, 1], c='red', label='Spam', edgecolors='k')# 绘制决策边界
# 创建一个网格
x_min, x_max = train_x_pca[:, 0].min() - 1, train_x_pca[:, 0].max() + 1
y_min, y_max = train_x_pca[:, 1].min() - 1, train_x_pca[:, 1].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 500),np.linspace(y_min, y_max, 500))# 计算决策函数值
Z = clf_pca.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)# 绘制决策边界和间隔带
plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors='green')
plt.contour(xx, yy, Z, levels=[-1, 1], linestyles='--', colors='gray')plt.legend()
plt.title('SVM Decision Boundary (PCA Reduced 2D)')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.show()
- 用 PCA 将高维特征压缩成 2 维空间。
- 使用 SVM 在这个低维空间重新训练一个模型(仅用于可视化)。
- 展示不同类别的点分布情况,以及 SVM 的分界线与间隔。
- 完整代码
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.io as scio
from sklearn import svm
import re #处理正则表达式的模块
import nltk #自然语言处理工具包
from sklearn.decomposition import PCA#查看样例邮件
f = open('emailSample1.txt', 'r').read()
print(f)def processEmail(email):email = email.lower() #转化为小写email = re.sub('<[^<>]+>', ' ', email) #移除所有HTML标签email = re.sub(r'(http|https)://[^\s]*', 'httpaddr', email) #将所有的URL替换为'httpaddr'email = re.sub(r'[^\s]+@[^\s]+', 'emailaddr', email) #将所有的地址替换为'emailaddr'email = re.sub(r'\d+', 'number', email) #将所有数字替换为'number'email = re.sub('[$]+', 'dollar', email) #将所有美元符号($)替换为'dollar'#将所有单词还原为词根//移除所有非文字类型,空格调整stemmer = nltk.stem.PorterStemmer() #使用Porter算法tokens = re.split(r'[ @$/#.-:&*+=\[\]?!()\{\},\'\">_<;%]', email) #把邮件分割成单个的字符串,[]里面为各种分隔符tokenlist = []for token in tokens:token = re.sub('[^a-zA-Z0-9]', '', token) #去掉任何非字母数字字符try: #porterStemmer有时会出现问题,因此用trytoken = stemmer.stem(token) #词根except:token = ''if len(token) < 1: continue #字符串长度小于1的不添加到tokenlist里tokenlist.append(token)return tokenlist#查看处理后的样例
processed_f = processEmail(f)
for i in processed_f:print(i, end=' ')#得到单词表,序号为索引号+1
vocab_list = np.loadtxt('vocab.txt', dtype='str', usecols=1)
#得到词汇表中的序号
def word_indices(processed_f, vocab_list):indices = []for i in range(len(processed_f)):for j in range(len(vocab_list)):if processed_f[i]!=vocab_list[j]:continueindices.append(j+1)return indices#查看样例序号
f_indices = word_indices(processed_f, vocab_list)
for i in f_indices:print(i, end=' ')def emailFeatures(indices):features = np.zeros((1899))for each in indices:features[each-1] = 1 #若indices在对应单词表的位置上词语存在则记为1return featuressum(emailFeatures(f_indices)) #45def emailFeatures(indices):features = np.zeros((1899))for each in indices:features[each-1] = 1 #若indices在对应单词表的位置上词语存在则记为1return featuressum(emailFeatures(f_indices)) #45#训练模型
train = scio.loadmat('spamTrain.mat')
train_x = train['X']
train_y = train['y']clf = svm.SVC(C=0.1, kernel='linear')
clf.fit(train_x, train_y)#精度
def accuracy(clf, x, y):predict_y = clf.predict(x)m = y.sizecount = 0for i in range(m):count = count + np.abs(int(predict_y[i])-int(y[i])) #避免溢出错误得到225return 1-float(count/m) train_accuracy = accuracy(clf, train_x, train_y) #0.99825
print("Train accuracy:", train_accuracy)#测试模型
test = scio.loadmat('spamTest.mat')test_accuracy = accuracy(clf, test['Xtest'], test['ytest']) #0.989
print("Test accuracy:", test_accuracy)#打印权重最高的前15个词,邮件中出现这些词更容易是垃圾邮件
i = (clf.coef_).size-1
while i >1883:#返回从小到大排序的索引,然后再打印print(vocab_list[np.argsort(clf.coef_).flatten()[i]], end=' ')i = i-1t = open('spamSample2.txt', 'r').read()
#预处理
processed_f = processEmail(t)
f_indices = word_indices(processed_f, vocab_list)
#特征提取
x = np.reshape(emailFeatures(f_indices), (1,1899))
#预测
clf.predict(x)# 载入训练数据
train = scio.loadmat('spamTrain.mat')
train_x = train['X']
train_y = train['y'].flatten() # 拉平成1维数组方便使用# 用线性核训练SVM
clf = svm.SVC(C=0.1, kernel='linear')
clf.fit(train_x, train_y)# PCA降维到2维
pca = PCA(n_components=2)
train_x_pca = pca.fit_transform(train_x)# 重新训练一个2维的SVM,用于绘制决策边界
clf_pca = svm.SVC(C=0.1, kernel='linear')
clf_pca.fit(train_x_pca, train_y)# 画图
plt.figure(figsize=(10, 6))# 绘制不同类别样本点
plt.scatter(train_x_pca[train_y==0, 0], train_x_pca[train_y==0, 1], c='blue', label='Non-spam', edgecolors='k')
plt.scatter(train_x_pca[train_y==1, 0], train_x_pca[train_y==1, 1], c='red', label='Spam', edgecolors='k')# 绘制决策边界
# 创建一个网格
x_min, x_max = train_x_pca[:, 0].min() - 1, train_x_pca[:, 0].max() + 1
y_min, y_max = train_x_pca[:, 1].min() - 1, train_x_pca[:, 1].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 500),np.linspace(y_min, y_max, 500))# 计算决策函数值
Z = clf_pca.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)# 绘制决策边界和间隔带
plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors='green')
plt.contour(xx, yy, Z, levels=[-1, 1], linestyles='--', colors='gray')plt.legend()
plt.title('SVM Decision Boundary (PCA Reduced 2D)')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.show()
3.运行结果

-
决策边界与支持向量带
绿色实线:SVM 的决策边界(分类超平面),表示模型判断垃圾/非垃圾邮件的分界线。
灰色虚线(上下各一条):代表 SVM 的“间隔边界”(margin)——支持向量带。
SVM 的目标就是最大化这两条边界之间的间隔(margin)。
落在虚线之间的点是支持向量,最影响决策边界的位置。 -
分类结果分布
红色点(Spam):预测为垃圾邮件
蓝色点(Non-spam):预测为非垃圾邮件
观察结果:
大部分红点和蓝点被成功分开,说明模型效果不错。
决策边界大致水平(沿 x 轴延展),说明分类器主要依据 PCA 的第 2 主成分 进行分类(也就是 y 轴方向)。
有少量红蓝点混杂,尤其靠近边界或 margin 区域,是分类难度较大的样本,也可能是误分类点。
相关文章:

机器学习:支持向量机(SVM)原理解析及垃圾邮件过滤实战
一、什么是支持向量机(SVM) 1. 基本概念 1.1 二分类问题的本质 在机器学习中,分类问题是最常见的任务之一。最简单的情况就是二分类:比如一封邮件是“垃圾邮件”还是“正常邮件”?一个病人是“患病”还是“健康”&a…...

LLM Agent 如何颠覆股价预测的传统范式
写在前面 股价预测,金融领域的“圣杯”之一,吸引了无数研究者和投资者。传统方法从技术指标到复杂的计量经济模型,再到机器学习,不断演进,但市场的高度复杂性、非线性和充斥噪声的特性,使得精准预测依然是巨大的挑战。大型语言模型(LLM)的崛起,特别是LLM Agent这一新…...

App/uni-app 离线本地存储方案有哪些?最推荐的是哪种方案?
以下是 UniApp 离线本地存储方案的详细介绍及推荐方案分析: 一、UniApp 离线本地存储方案分类 1. 基于 uni.storage 系列 API(跨端基础方案) API 及特点: 提供 uni.setStorage(异步存储)、uni.getStorag…...

【案例分享】如何借助JS UI组件库DHTMLX Suite构建高效物联网IIoT平台
随着工业领域数字化进程的持续加快,Web 技术在实现实时监控、数据可视化与控制系统等方面正扮演着越来越核心的角色。来自智利的科技企业 Wise Data Global 就是这一趋势中的积极践行者。他们借助慧都科技代理的 DHTMLX Suite JavaScript UI 控件库,为遥…...

Skia如何绘制几何图形
应用程序(网页、桌面应用或移动应用)大多数都是由基本的几何图形构成的。那我们该如何使用 Skia 绘制基本的几何图形。 画矩形 void drawRect(SkCanvas* canvas) {SkPaint paint;paint.setColor(SK_ColorRED);paint.setStroke(true);paint.setStrokeWid…...

spring:实例化类过程中方法执行顺序。
如题。在实例化Bean时,会根据配置依次调用方法。在此测试代码如下: 在测试类中继承接口InitializingBean,接口InterfaceUserService(该接口为自定义,只是定义set方法)。 InterfaceUserService,…...

设置应用程序图标
(1)找一张图片 (2)然后转ico图片 在线生成透明ICO图标——ICO图标制作 验证16x16就可以 降低exe大小 (3) 在xxx.pro修改 添加 (4) 删除 build 和 xxxpro_user文件 (5)编译project 和运行xx.exe (6)右键 设置快捷方式...
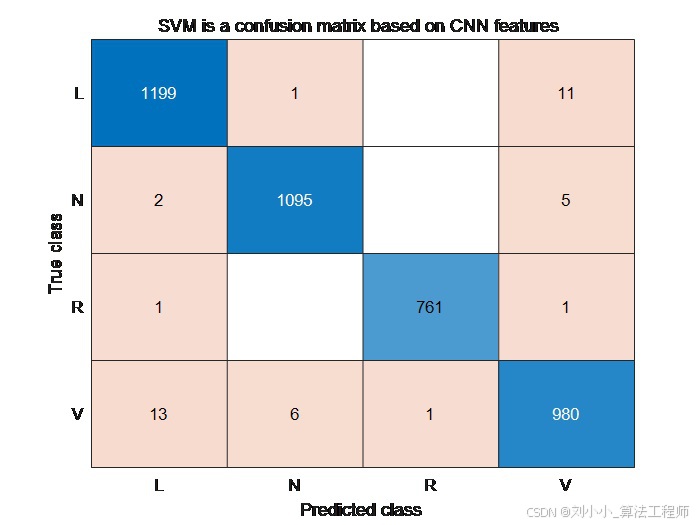
「基于连续小波变换(CWT)和卷积神经网络(CNN)的心律失常分类算法——ECG信号处理-第十五课」2025年6月6日
一、引言 心律失常是心血管疾病的重要表现形式,其准确分类对临床诊断具有关键意义。传统的心律失常分类方法主要依赖于人工特征提取和经典机器学习算法,但这些方法往往受限于特征选择的主观性和模型的泛化能力。 随着深度学习技术的发展,基于…...

用go从零构建写一个RPC(4)--gonet网络框架重构+聚集发包
在追求高性能的分布式系统中,RPC 框架的底层网络能力和数据传输效率起着决定性作用。经过几轮迭代优化,我完成了第四版本的 RPC 框架。相比以往版本,这一版本的最大亮点在于 重写了底层网络框架 和 实现了发送端的数据聚集机制,这…...

OpenBayes 一周速览|TransPixeler 实现透明化文本到视频生成;统一图像定制框架 DreamO 上线,一键处理多种图像生成任务
公共资源速递 2 个公共数据集: * s1K-1.1 数学推理数据集 * HPA 人类蛋白质图谱数据集 3 个公共模型: * MedGemma-4B-IT * Devstral-Small-2505 * DeepSeek-Prover-V2-7B 12 个公共教程: 视频生成 * 2 语音交互 * 3 代码生成 * 3 …...

视频的分片上传,断点上传
上传功能的实现,点击上传按钮,判断添加的文件是否符合要求,如果符合把他放入文件列表中,并把他的状态设置为等待中,对于每个文件,把他们切分为chunksize大小的文件片段,再检查他的状态是否为…...

CSS 性能优化
目录 CSS 性能优化CSS 提高性能的方法1. 选择器优化1.1 选择器性能原则1.2 选择器优化示例 2. 重排(Reflow)和重绘(Repaint)优化2.1 重排和重绘的概念2.2 触发重排的操作2.3 触发重绘的操作2.4 优化重排和重绘的方法 3. 资源优化3…...

华为×小鹏战略合作:破局智能驾驶深水区的商业逻辑深度解析
当中国智能电动车竞争进入下半场,头部玩家的合纵连横正在重构产业格局。华为与小鹏汽车近日官宣的“战略合作”,表面看是技术互补的常规操作,实则暗藏改写行业游戏规则的深层商业逻辑。 一、技术破壁:从“单点突破”到“全栈协同”…...

4D毫米波雷达产品推荐
供应商链接 :https://mp.weixin.qq.com/s/GYarrc9VEZS0FafxRUeG9w 大陆 ARS548 采埃孚 博世 安波福 -------- Waymo MobileEye 华为(未找到官网资料) ------- 森思泰克 http://www.whst.com/contact.html 芜湖经济技术开发区东区…...

yolo 训练 中间可视化
yolo训练前几个batch,会可视化target: if plots and ni < 33:f save_dir / ftrain_batch{ni}.jpg # filenameplot_images(imgs, targets, paths, f, kpt_labelkpt_label)...

Rust 学习笔记:关于 Cargo 的练习题
Rust 学习笔记:关于 Cargo 的练习题 Rust 学习笔记:关于 Cargo 的练习题问题一问题二问题三问题四问题五问题六问题七 Rust 学习笔记:关于 Cargo 的练习题 参考视频: https://www.bilibili.com/video/BV1xjAaeAEUzhttps://www.b…...
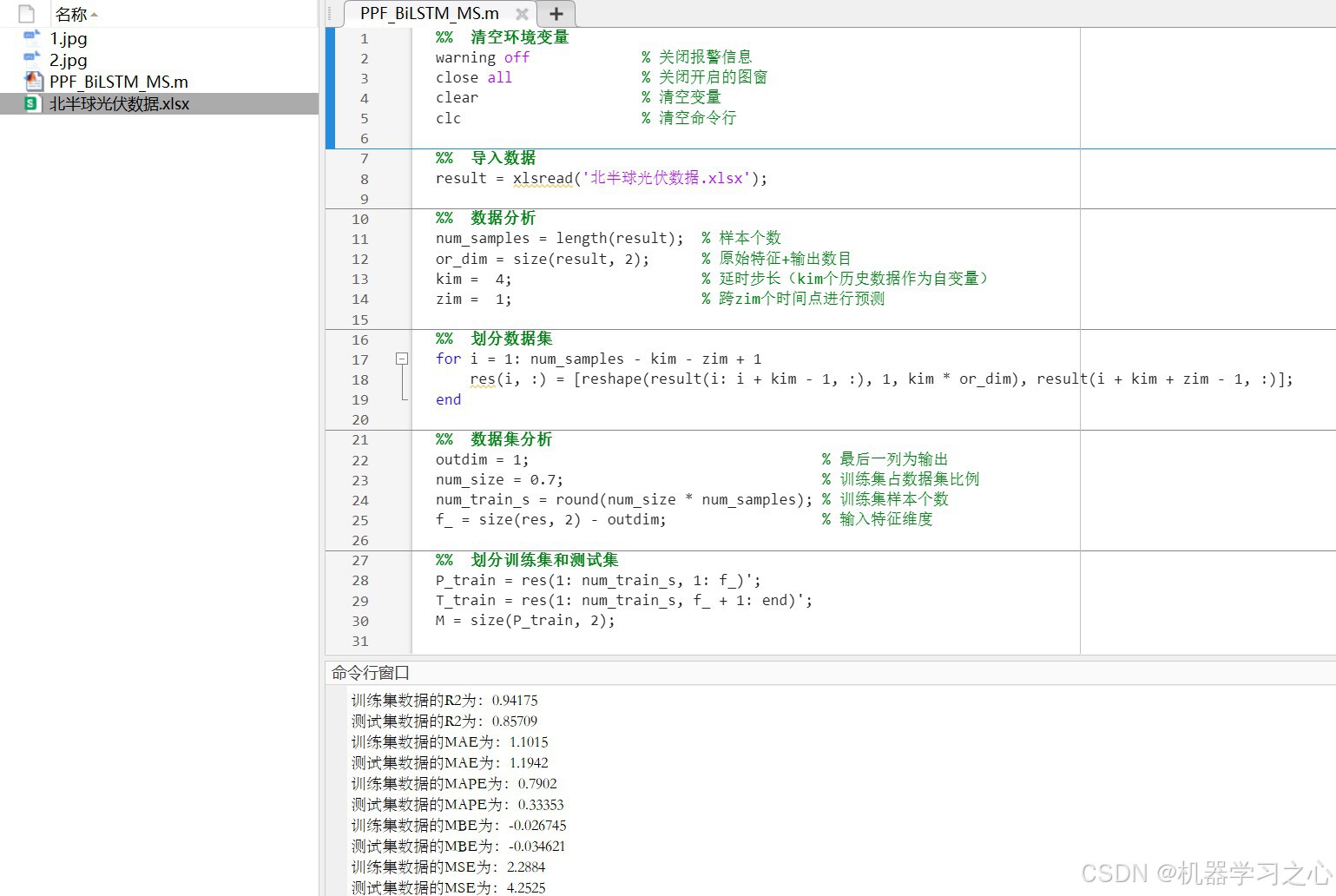
光伏功率预测 | BiLSTM多变量单步光伏功率预测(Matlab完整源码和数据)
光伏功率预测 | BiLSTM多变量单步光伏功率预测(Matlab完整源码和数据) 目录 光伏功率预测 | BiLSTM多变量单步光伏功率预测(Matlab完整源码和数据)效果一览基本介绍程序设计参考资料 效果一览 基本介绍 光伏功率预测 | BiLSTM多变…...

20250606-C#知识:委托和事件
C#知识:委托和事件 使用委托可以很方便地调用多个方法,也方便将方法作为参数进行传递 1、委托 委托是方法的容器委托可以看作一种特殊的类先定义委托类,再用委托类声明委托变量,委托变量可以存储方法 delegate int Calculate(in…...

AI数字人技术革新进行时:井云数字人如何重塑人机交互未来?
老板们注意了!不用反复真人出镜拍摄,AI数字人来帮你做口播,只需3分钟克隆你的形象和声音,输入文案24小时随时都能生成视频! 在元宇宙概念持续升温、虚拟与现实加速融合的当下,AI数字人正以惊人的速度从科幻…...

ruoyi-plus-could 负载均衡 通过 Gateway模块配置负载均衡
这个很简单的,其实都不用配置。 在nacos中ruoyi-gateway.yml配置文件里面: 其实他已经给我们配置好了,只要uri:lb有【lb】就表示负载均衡配置 我们只需要在启动服务的时候改下端口就可以。 然后通过小工具测试下: 结…...

江科大读写内部flash到hal库实现
hal库相关代码 进程结构体 typedef struct {__IO FLASH_ProcedureTypeDef ProcedureOnGoing; /*表示闪存操作过程中的不同状态或过程类型*/__IO uint32_t DataRemaining; /*记录尚未完成的页数或者半字数*/__IO uint32_t Address; /…...

Matlab回归预测大合集又更新啦!新增2种高斯过程回归预测模型,已更新41个模型!性价比拉满!
Matlab回归预测大合集又更新啦!新增2种高斯过程回归预测模型,已更新41个模型!性价比拉满! 目录 Matlab回归预测大合集又更新啦!新增2种高斯过程回归预测模型,已更新41个模型!性价比拉满…...

主流 AI IDE 之一的 Cursor 介绍
一、什么是 Cursor Cursor 是由 Anysphere 公司开发的 AI 驱动的代码编辑器(IDE);Anysphere 成立于 2022 年,创始团队包括来自麻省理工学院(MIT)的毕业生,如联合创始人 Aman Sanger 和 Michael …...

0x-1 记一次SGA PGA设置失败,重新开库
0、生产侧定时平台上传数据库11g hang,修改无法startup 厂商统一发放的虚拟机作为前置机导入平台后,直接开机使用。主机在虚拟化平台中,实例卡死后,按照虚拟机系统64G,原SGA2g,不知哪个大聪明给默认设置的。保守计划修…...
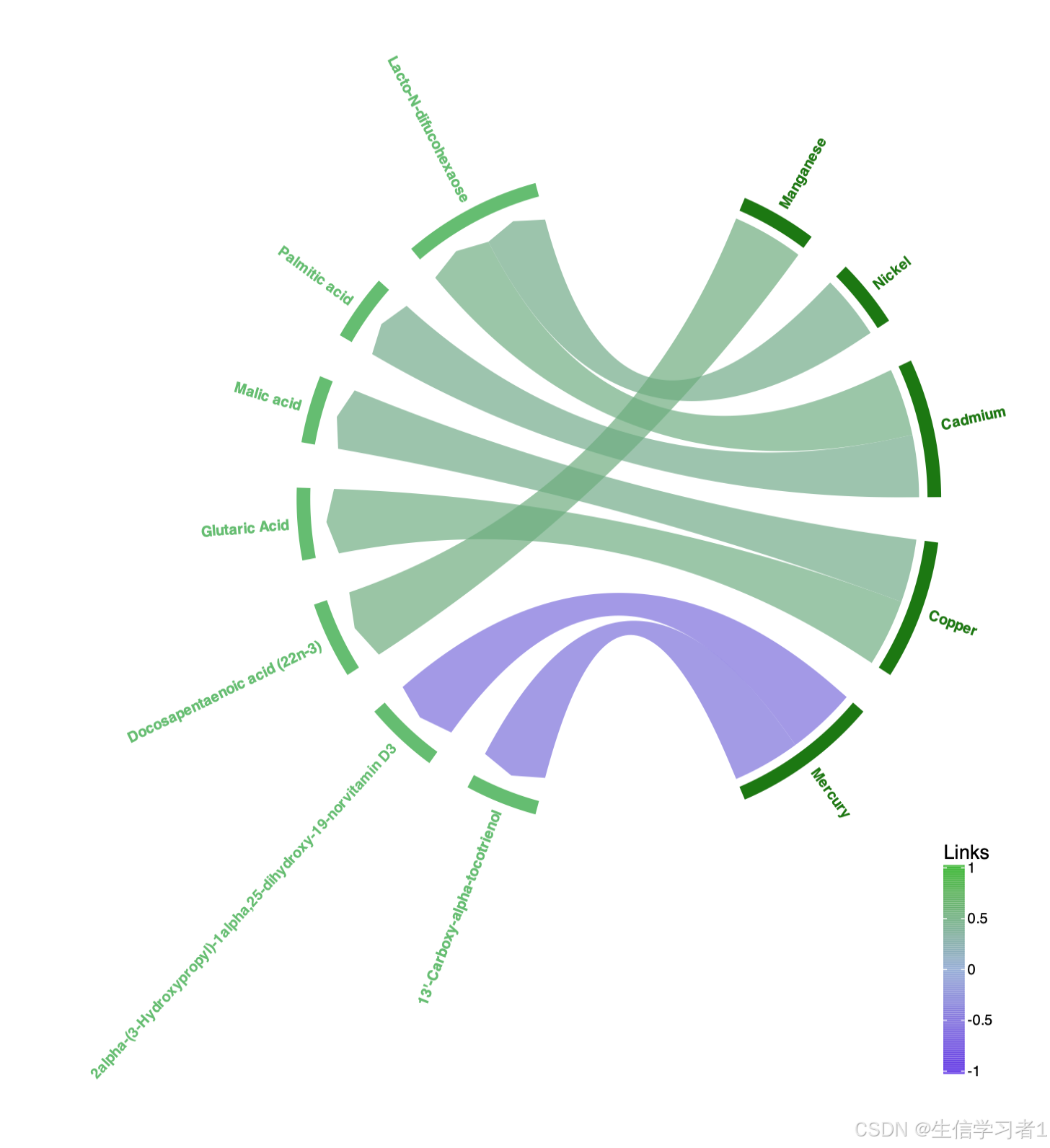
【科研绘图系列】R语言绘制和弦图(Chord diagram plot)
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍加载R包数据下载导入数据数据预处理相关性计算和弦图系统信息介绍 本文介绍了一个基于R语言的数据分析和可视化流程,主要用于生成和弦图(Chord Diagram)。和弦图是一种用于展示…...
PPT转图片拼贴工具 v3.0
软件介绍 这个软件就是将PPT文件转换为图片并且拼接起来。 这个代码支持导入单个文件也支持导入文件夹 但是目前还没有解决可视化界面问题。 效果展示 软件源码 import os import re import win32com.client from PIL import Image from typing import List, Uniondef con…...

关于安科瑞APD局部放电监测装置解决方案的应用分析
1 什么是局部放电? 局部放电(Partial Discharge, PD)是指发生在电气设备绝缘系统局部区域的、未贯穿整个电极的微小放电现象。它通常发生在高压电气设备(如变压器、开关柜、电缆、GIS等)内部存在绝缘缺陷、电场集中或…...
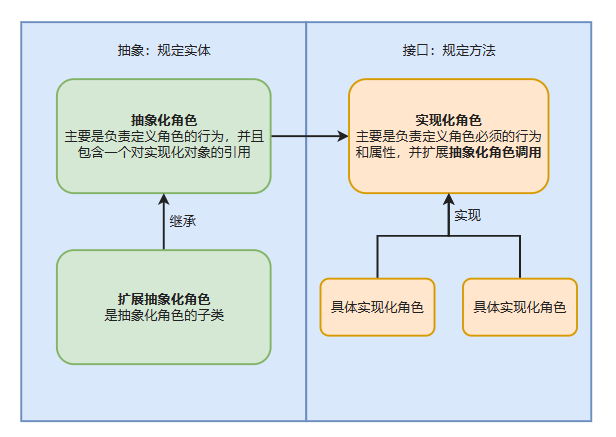
设计模式-2 结构型模式
一、代理模式 1、举例 海外代购 2、代理基本结构图 3、静态代理 1、真实类实现一个接口,代理类也实现这个接口。 2、代理类通过真实对象调用真实类的方法。 4、静态代理和动态代理的区别 1、静态代理在编译时就已经实现了,编译完成后代理类是一个实际…...

大量企业系统超龄服役!R²AIN SUITE 一体化企业提效解决方案重构零售数智化基因
《中国百货商业协会2024零售IT及数字化系统需求调查报告》为我们呈现了零售企业在数字化转型中的复杂图景。数据显示,82%的企业高管对AI改变行业未来充满信心 source:中国百货商业协会 ,零售IT及数字化系统需求调查报告 ,2024年 但…...

Cesium使用glb模型、图片标记来实现实时轨迹
目录 1、使用glb模型进行实时轨迹 2、使用图片进行实时轨迹 基于上一篇加载基础地图的代码上继续开发 vue中加载Cesium地图(天地图、高德地图)-CSDN博客文章浏览阅读164次。vue中加载Cesium三维地球https://blog.csdn.net/ssy001128/article/details…...
