【大模型LLM学习】Flash-Attention的学习记录
【大模型LLM学习】Flash-Attention的学习记录
- 0. 前言
- 1. flash-attention原理简述
- 2. 从softmax到online softmax
- 2.1 safe-softmax
- 2.2 3-pass safe softmax
- 2.3 Online softmax
- 2.4 Flash-attention
- 2.5 Flash-attention tiling
0. 前言
Flash Attention可以节约模型训练和推理时间,很多模型可以通过config参数来选择attention是标准的attention实现还是flash-attention方式。在这里记录一下flash attention的学习过程,发现了一位博主以及参考的资料特别好:
- zhihu一位做高性能计算的博主博文
- 华盛顿大学的课程note
1. flash-attention原理简述
a t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) V attention(Q,K,V)=softmax\left(\frac{QK^T}{\sqrt{d_k}}\right)V attention(Q,K,V)=softmax(dkQKT)V
标准的attention操作的时间卡点不是在运算上,而是卡在数据读写上。SRAM的读写速度快,但是存储空间有限,无法一次存下来所有的中间计算结果,一次attention计算存在SRAM<->HBM的多次读写操作。
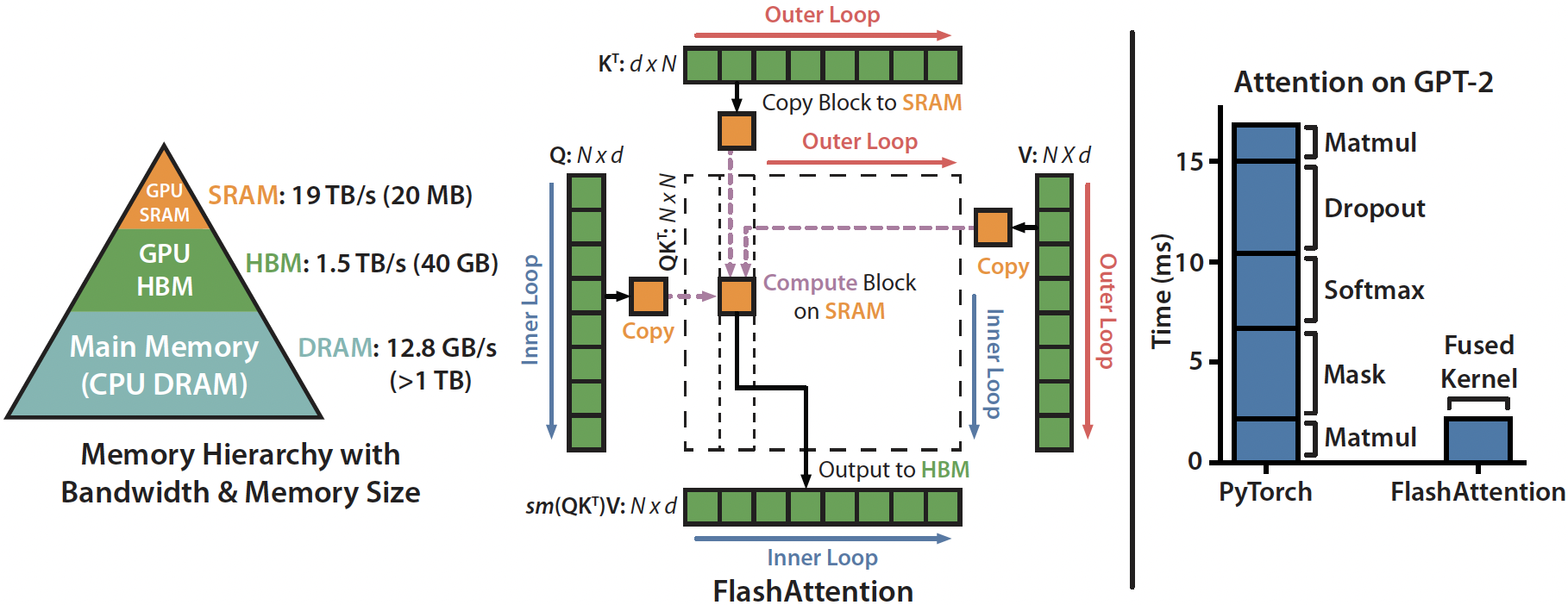
与标准的attention操作比较,flash-attention通过减少数据在HBM和SRAM间的读写操作,来节约时间(甚至backward时还进行了重新计算,重新计算的速度也比把数据从HBM读取到SRAM要快)。

2. 从softmax到online softmax
直接看flash-attention的论文比较难看明白,发现华盛顿大学的那份note写得特别清晰,跟着它从softmax看到flash-attention会比较容易。
2.1 safe-softmax
首先是safe的softmax计算方式。原始的softmax,对于N个数:
s o f t m a x ( { x 1 , . . . , x N } ) = { e x i ∑ j = 1 N e x j } i = 1 N softmax(\{x_1,...,x_N\})=\left\{\frac{e^{x_i}}{\sum_{j=1}^{N}e^{x_j}}\right\}_{i=1}^{N} softmax({x1,...,xN})={∑j=1Nexjexi}i=1N
对于FP16,最大能表示的数据为65536,当 x > = 11 x>=11 x>=11时, e x e^x ex就会超过FP16的最大表示范围影响结果的正确性。为了避免这个问题,SafeSoftmax 通过减去输入向量中的最大值来调整输入,使得最大的指数项变为 e 0 = 1 e^0=1 e0=1从而防止了上溢的发生。同时,由于所有的指数项都除以同一个数,它们的比例关系不会改变,因此也不会影响最终的概率分布。
e x i ∑ j = 1 N e x j = e x i − m ∑ j = 1 N e x j − m , m = m a x { x j } j = 1 N \frac{e^{x_i}}{\sum_{j=1}{N}e^{x_j}}=\frac{e^{x_i-m}}{\sum_{j=1}{N}e^{x_j-m}}, \quad m=max\left\{x_j\right\}_{j=1}^{N} ∑j=1Nexjexi=∑j=1Nexj−mexi−m,m=max{xj}j=1N
2.2 3-pass safe softmax
- 对于一个行向量 { x i } i = 1 N \{x_i\}_{i=1}^N {xi}i=1N,最直白的softmax计算方式是直接for循环

这个算法计算softmax需要执行3次从1->N的循环,在attention中, { x i } \{x_i\} {xi}是 Q K T QK^T QKT的结果,但是如果SRAM里面存不下这个大的矩阵,上面的计算过程,就需要从HBM里面加载3次 { x i } \{x_i\} {xi},时间花在了数据读写上。
2.3 Online softmax
如果能把上面(7)(8)(9)这3个式子的计算放一个for循环,就只需要一次load数据。但是 m N m_N mN是全局最大值,计算 m N m_N mN就已经需要一次遍历了。
Online softmax算法把(7)(8)进行了合并,把3次遍历缩减为2个。它提出计算 d i ′ = ∑ j = 1 i e x j − m i d_i^{\prime}=\sum_{j=1}^{i}e^{x_j-m_i} di′=∑j=1iexj−mi来代替计算 d i d_i di,当算到最后 i = N i=N i=N时会发现, d N = d N ′ d_N=d_N^{\prime} dN=dN′。具体的,迭代计算 d i ′ d_i^{\prime} di′的方式为:
d i ′ = ∑ j = 1 i e x j − m i = ( ∑ j = 1 i − 1 e x j − m i ) + e x i − m i = ( ∑ j = 1 i − 1 e x j − m i − 1 ) e m i − 1 − m i + e x i − m i = d i − 1 ′ e m i − 1 − m i + e x i − m i \begin{aligned} d_i^{\prime} &= \sum_{j=1}^{i} e^{x_j - m_i} \\ &= \left( \sum_{j=1}^{i-1} e^{x_j - m_i} \right) + e^{x_i - m_i} \\ &= \left( \sum_{j=1}^{i-1} e^{x_j - m_{i-1}} \right) e^{m_{i-1} - m_i} + e^{x_i - m_i} \\ &= d_{i-1}^{\prime} e^{m_{i-1} - m_i} + e^{x_i - m_i} \end{aligned} di′=j=1∑iexj−mi=(j=1∑i−1exj−mi)+exi−mi=(j=1∑i−1exj−mi−1)emi−1−mi+exi−mi=di−1′emi−1−mi+exi−mi
所以就可以用迭代的方式,在找最大值 m N m_N mN的时候,同时来计算 d i ′ d_i^{\prime} di′,把(7)和(8)一起计算,这样只需要加载两次 x i x_i xi。

2.4 Flash-attention
上面的online softmax仍然需要2个for循环,加载2次 x i x_i xi来完成softmax的计算。完成softmax的计算,没法更进一步地压缩到1次遍历。但是attention计算的最终目标是获取输出结果,也就是注意力分数与 V V V相乘的结果 O = A × V O=A \times V O=A×V,计算 O O O可以通过一次遍历完成。

可以使用类似online softmax把计算 d i d_i di变成计算 d i ′ d_i^{\prime} di′的方式,把 o i o_i oi的计算也改成迭代式的,首先把 a i a_i ai带入 o i o_i oi的表达式
o i = ∑ j = 1 i ( e x j − m N d N ′ V [ j , : ] ) o_i=\sum_{j=1}^{i}\left(\frac{e^{x_j-m_{N}}}{d_N^{\prime}}V[j,:]\right) oi=j=1∑i(dN′exj−mNV[j,:])
可以找到一个 o i ′ o_i^{\prime} oi′,它不依赖于全局的 d N ′ d_N^{\prime} dN′和 m N m_N mN
o i ′ = ∑ j = 1 i ( e x j − m i d i ′ V [ j , : ] ) o_i^{\prime}=\sum_{j=1}^{i}\left(\frac{e^{x_j-m_{i}}}{d_i^{\prime}}V[j,:]\right) oi′=j=1∑i(di′exj−miV[j,:])
对于 o i ′ o_i^{\prime} oi′的计算可以使用迭代的方式,同样的是有 o N = o N ′ o_N=o_N^{\prime} oN=oN′
o i ′ = ∑ j = 1 i e x j − m i d i ′ V [ j , : ] = ( ∑ j = 1 i − 1 e x j − m i d i ′ V [ j , : ] ) + e x i − m i d i ′ V [ i , : ] = ( ∑ j = 1 i − 1 e x j − m i − 1 d i − 1 ′ e x j − m i e x j − m i − 1 d i − 1 ′ d i ′ V [ j , : ] ) + e x i − m i d i ′ V [ i , : ] = ( ∑ j = 1 i − 1 e x j − m i − 1 d i − 1 ′ V [ j , : ] ) d i − 1 ′ d i ′ e m i − 1 − m i + e x i − m i d i ′ V [ i , : ] = o i − 1 ′ d i − 1 ′ e m i − 1 − m i d i ′ + e x i − m i d i ′ V [ i , : ] \begin{aligned} o_i' &= \sum_{j=1}^{i} \frac{e^{x_j - m_i}}{d_i'} V[j,:] \\ &= \left( \sum_{j=1}^{i-1} \frac{e^{x_j - m_i}}{d_i'} V[j,:] \right) + \frac{e^{x_i - m_i}}{d_i'} V[i,:] \\ &= \left( \sum_{j=1}^{i-1} \frac{e^{x_j - m_{i-1}}}{d_{i-1}'} \frac{e^{x_j - m_i}}{e^{x_j - m_{i-1}}} \frac{d_{i-1}'}{d_i'} V[j,:] \right) + \frac{e^{x_i - m_i}}{d_i'} V[i,:] \\ &= \left( \sum_{j=1}^{i-1} \frac{e^{x_j - m_{i-1}}}{d_{i-1}'} V[j,:] \right) \frac{d_{i-1}'}{d_i'} e^{m_{i-1} - m_i} + \frac{e^{x_i - m_i}}{d_i'} V[i,:] \\ &= o_{i-1}' \frac{d_{i-1}' e^{m_{i-1} - m_i}}{d_i'} + \frac{e^{x_i - m_i}}{d_i'} V[i,:] \end{aligned} oi′=j=1∑idi′exj−miV[j,:]=(j=1∑i−1di′exj−miV[j,:])+di′exi−miV[i,:]=(j=1∑i−1di−1′exj−mi−1exj−mi−1exj−midi′di−1′V[j,:])+di′exi−miV[i,:]=(j=1∑i−1di−1′exj−mi−1V[j,:])di′di−1′emi−1−mi+di′exi−miV[i,:]=oi−1′di′di−1′emi−1−mi+di′exi−miV[i,:]
这样计算attention的输出结果可以只进行一次遍历就完成

2.5 Flash-attention tiling
上面是每次计算一个元素 [ i ] [i] [i],实际上可以一次读取一个大小为b的块(tile)来计算


此外,在flash-attention的paper里面,对 Q Q Q、 K K K、 V V V和 O O O分块,其中 Q Q Q
和 O O O每块大小为 m i n ( M / 4 d , d ) × d min(M/4d,d) \times d min(M/4d,d)×d, K / V K/V K/V的每块大小为 M / 4 d × d M/4d \times d M/4d×d,加起来正好不会超过SRAM的大小M,完整的算法在paper中:

相关文章:

【大模型LLM学习】Flash-Attention的学习记录
【大模型LLM学习】Flash-Attention的学习记录 0. 前言1. flash-attention原理简述2. 从softmax到online softmax2.1 safe-softmax2.2 3-pass safe softmax2.3 Online softmax2.4 Flash-attention2.5 Flash-attention tiling 0. 前言 Flash Attention可以节约模型训练和推理时间…...

三、元器件的选型
前言:我们确立了题目的功能后,就可以开始元器件的选型,元器件的选型关乎到我们后面代码编写的一个难易。 一、主控的选择 主控的选择很大程度上决定我们后续使用的代码编译器,比如ESP32使用的是VScode,或者Arduino&a…...
:Socialight的定价转型启示——B2B商业模式的价格策略与利润优化)
精益数据分析(95/126):Socialight的定价转型启示——B2B商业模式的价格策略与利润优化
精益数据分析(95/126):Socialight的定价转型启示——B2B商业模式的价格策略与利润优化 在创业过程中,从B2C转向B2B不仅是商业模式的转变,更是定价策略与成本结构的全面重构。今天,我们将通过Socialight的实…...

stm32_DMA
DMA 1. 概念与基本原理 DMA,全称Direct Memory Access,即直接存储器访问。它是微控制器(MCU)、嵌入式处理器中的一个独立硬件模块,用于在无需CPU干预的情况下,在不同内存区域(包括外设寄存器和…...

物联网数据归档之数据存储方案选择分析
在上一篇文章中《物联网数据归档方案选择分析》中凯哥分析了归档设计的两种方案,并对两种方案进行了对比。这篇文章咱们就来分析分析,归档后数据应该存储在哪里?及存储方案对比。 这里就选择常用的mysql及taos数据库来存储归档后的数据吧。 你在处理设备归档表存储方案时对…...

【自动驾驶避障开发】如何让障碍物在 RViz 中‘显形’?呈现感知数据转 Polygon 全流程
【自动驾驶避障开发】如何让障碍物在 RViz 中"显形"?呈现感知数据转 Polygon 全流程 自动驾驶系统中的障碍物可视化是开发调试过程中至关重要的一环。本文将详细介绍如何将自动驾驶感知模块检测到的障碍物数据转换为RViz可显示的Polygon(多边形)形式,实现障碍物…...

【C语言】C语言经典小游戏:贪吃蛇(上)
文章目录 一、游戏背景及其功能二、Win32 API介绍1、Win32 API2、控制台程序3、定位坐标(COORD)4、获得句柄(GetStdHandle)5、获得光标属性(GetConsoleCursorInfo)1)描述光标属性(CO…...

usbutils工具的使用帮助
作为嵌入式系统开发中的常用工具,usbutils 是一套用于管理和调试USB设备的Linux命令行工具集。以下是其核心功能和使用方法的详细说明: 1. 工具组成 核心命令: lsusb:列出所有连接的USB设备及详细信息(默认安装&#…...

vue2中使用jspdf插件实现页面自定义块pdf下载
pdf下载 实现pdf下载的环境安装jspdf插件在项目中使用 实现pdf下载的环境 项目需求案例背景,点击【pdf下载】按钮,弹出pdf下载弹窗,显示需要下载四个模块的下载进度,下载完成后,关闭弹窗即可! 项目使用的是…...

如何防止服务器被用于僵尸网络(Botnet)攻击 ?
防止服务器被用于僵尸网络(Botnet)攻击是关键的网络安全措施之一。僵尸网络是黑客利用大量被感染的计算机、服务器或物联网设备来发起攻击的网络。以下是关于如何防止服务器被用于僵尸网络攻击的技术文章: 防止服务器被用于僵尸网络ÿ…...
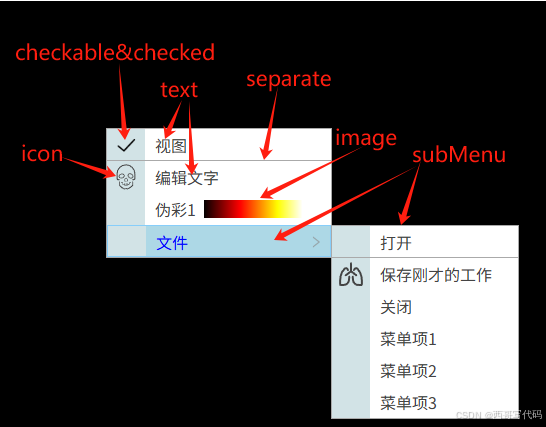
基于cornerstone3D的dicom影像浏览器 第二十九章 自定义菜单组件
文章目录 前言一、程序结构1. 菜单数据结构2. XMenu.vue3. XSubMenu.vue4. XSubMenuSlot.vue5. XMenuItem.vue 二、调用流程总结 前言 菜单用于组织程序功能,为用户提供导航。是用户与程序交互非常重要的接口。 开源组件库像Element Plus和Ant Design中都提供了功能…...

【Block总结】DBlock,结合膨胀空间注意模块(Di-SpAM)和频域模块Gated-FFN|即插即用|CVPR2025
论文信息 标题: DarkIR: Robust Low-Light Image Restoration 作者: Daniel Feijoo, Juan C. Benito, Alvaro Garcia, Marcos Conde 论文链接:https://arxiv.org/pdf/2412.13443 GitHub链接:https://github.com/cidautai/DarkIR 创新点 DarkIR提出了…...

【学习笔记】单例类模板
【学习笔记】单例类模板 一、单例类模板 以下为一个通用的单例模式框架,这种设计允许其他类通过继承Singleton模板类来轻松实现单例模式,而无需为每个类重复编写单例实现代码。 // 命名空间(Namespace) 和 模板(Tem…...
)
字符串加密(华为OD)
题目描述 给你一串未加密的字符串str,通过对字符串的每一个字母进行改变来实现加密,加密方式是在每一个字母str[i]偏移特定数组元素a[i]的量,数组a前三位已经赋值:a[0]=1,a[1]=2,a[2]=4。当i>=3时,数组元素a[i]=a[i-1]+a[i-2]+a[i-3]。例如:原文 abcde 加密后 bdgkr,…...

口罩佩戴检测算法AI智能分析网关V4工厂/工业等多场景守护公共卫生安全
一、引言 在公共卫生安全日益受到重视的当下,口罩佩戴成为预防病毒传播、保障人员健康的重要措施。为了高效、精准地实现对人员口罩佩戴情况的监测,AI智能分析网关V4口罩检测方案应运而生。该方案依托先进的人工智能技术与强大的硬件性能,…...

Double/Debiased Machine Learning
独立同步分布的观测数据 { W i ( Y i , D i , X i ) ∣ i ∈ { 1 , . . . , n } } \{W_i(Y_i,D_i,X_i)| i\in \{1,...,n\}\} {Wi(Yi,Di,Xi)∣i∈{1,...,n}},其中 Y i Y_i Yi表示结果变量, D i D_i Di表示因变量, X i X_i Xi表…...

HarmonyOS Next 弹窗系列教程(4)
HarmonyOS Next 弹窗系列教程(4) 介绍 本章主要介绍和用户点击关联更加密切的菜单控制(Menu) 和 气泡提示(Popup) 它们出现显示弹窗出现的位置都是在用户点击屏幕的位置相关 菜单控制(Menu&…...

【C】-递归
1、递归概念 递归(Recursion)是编程中一种重要的解决问题的方法,其核心思想是函数通过调用自身来解决规模更小的子问题,直到达到最小的、可以直接解决的基准情形(Base Case)。 核心:自己调用…...

飞马LiDAR500雷达数据预处理
0 引言 在使用飞马D2000无人机搭载LiDAR500进行作业完成后,需要对数据进行预处理,方便给内业人员开展点云分类等工作。在开始操作前,先了解一下使用的软硬件及整体流程。 0.1 外业测量设备 无人机:飞马D2000S激光模块ÿ…...

Kerberos面试内容整理-在 Linux/Windows 中的 Kerberos 实践
Windows 实践: 在Windows环境中,Kerberos 几乎是无形融合的。用户使用域账号登录计算机时,实际上就完成了Kerberos的AS认证并获取TGT;此后的资源访问(如共享文件夹、打印机、数据库等)都会自动使用Kerberos进行验证,而无需用户干预。Windows通过LSASS进程维护和缓存用户…...
已创建的 **Module** 的操作指南)
在 Allegro PCB Editor 中取消(解除或删除)已创建的 **Module** 的操作指南
在 Allegro PCB Editor 中取消(解除或删除)已创建的 Module 有两种主要场景,操作也不同: 📌 场景一:仅想解除元件与 Module 的关联(保留元件位置和布线,但可独立编辑) …...

基于springboot的校园社团信息系统的设计与实现
其他源码获取可以看首页:代码老y 个人简介:专注于毕业设计项目定制开发:springbootvue系统,Java微信小程序,javaSSM系统等技术开发,并提供远程调试部署、代码讲解、文档指导、ppt制作等技术指导。源码获取&…...

nodejs里面的http模块介绍和使用
Node.js的http模块是构建在libuv库之上,以JavaScript接口形式暴露出来的核心模块之一,它允许开发者轻松地创建和管理HTTP服务器及客户端,进而实现网络应用的快速开发。此模块的设计理念围绕着事件驱动和非阻塞I/O模型,这些特性使N…...

mamba架构和transformer区别
Mamba 架构和 Transformer 架构存在多方面的区别,具体如下: 计算复杂度1 Transformer:自注意力机制的计算量会随着上下文长度的增加呈平方级增长,例如上下文增加 32 倍时,计算量可能增长 1000 倍,在处理长序…...

嵌入式鸿蒙开发环境搭建操作方法与实现
Linux环境搭建镜像下载链接: 链接:https://pan.baidu.com/s/1F2f8ED5V1KwLjyYzKVx2yQ 提取码:Leun vscode和Linux系统连接的详细过程1.下载Visual Studio Code...

在 Spring Boot 中使用 WebFilter:实现请求拦截、日志记录、跨域处理等通用逻辑!
💡 前言 在开发 Web 应用时,我们经常需要对所有请求进行统一处理,例如: 记录请求日志实现跨域(CORS)接口权限控制请求参数预处理防止 XSS 攻击 这些功能如果都写在每个 Controller 或 Service 里&#x…...
)
CSS预处理器:Sass与Less的语法和特性(含实际案例)
Sass(SCSS语法示例) 1. 变量:统一管理颜色 // 定义变量 $primary-color: #1a237e; $success-color: #4caf50; $font-size-base: 16px;// 实际应用 body {color: $primary-color;font-size: $font-size-base; }.button {background: $succes…...

QT常用控件(1)
控件是构成QT的基础元素,例如Qwidget也是一个控件,提供了一个‘空’的矩形,我们可以往里面添加内容和处理用户输入,例如:按钮(QpushButton),基础显示控件(Lableÿ…...

明基编程显示器终于有优惠了,程序员快来,错过等一年!
最近618的活动已经陆续开始了,好多人说这是买数码产品的好时候,作为一名资深程序员,我做了不少功课,决定给自己升级办公设备,入手明基 RD 系列的显示器,这是市面上首家专注于我们程序员痛点和需求的产品&am…...

【计算机网络】非阻塞IO——select实现多路转接
🔥个人主页🔥:孤寂大仙V 🌈收录专栏🌈:计算机网络 🌹往期回顾🌹:【计算机网络】NAT、代理服务器、内网穿透、内网打洞、局域网中交换机 🔖流水不争࿰…...
