[蓝桥杯]通电
通电
题目描述
2015 年,全中国实现了户户通电。作为一名电力建设者,小明正在帮助一带一路上的国家通电。
这一次,小明要帮助 nn 个村庄通电,其中 1 号村庄正好可以建立一个发电站,所发的电足够所有村庄使用。
现在,这 nn 个村庄之间都没有电线相连,小明主要要做的是架设电线连接这些村庄,使得所有村庄都直接或间接的与发电站相通。
小明测量了所有村庄的位置(坐标)和高度,如果要连接两个村庄,小明需要花费两个村庄之间的坐标距离加上高度差的平方,形式化描述为坐标为(x1,y1x1,y1) 高度为 h1h1 的村庄与坐标为 (x2,y2x2,y2) 高度为 h2h2 的村庄之间连接的费用为
(x1−x2)2+(y1−y2)2+(h1−h2)2(x1−x2)2+(y1−y2)2+(h1−h2)2
高度的计算方式与横纵坐标的计算方式不同。
由于经费有限,请帮助小明计算他至少要花费多少费用才能使这 nn 个村庄都通电。
输入描述
输入的第一行包含一个整数 nn ,表示村庄的数量。
接下来 nn 行,每个三个整数 x,y,hx,y,h,分别表示一个村庄的横、纵坐标和高度,其中第一个村庄可以建立发电站。
其中,1≤n≤1000,0≤x,y,h≤100001≤n≤1000,0≤x,y,h≤10000。
输出描述
输出一行,包含一个实数,四舍五入保留 2 位小数,表示答案。
输入输出样例
示例
输入
4
1 1 3
9 9 7
8 8 6
4 5 4
输出
17.41
运行限制
- 最大运行时间:1s
- 最大运行内存: 256M
总通过次数: 1434 | 总提交次数: 1697 | 通过率: 84.5%
难度: 困难 标签: 2020, 最小生成树, 省模拟赛
C++实现村庄通电问题:最小生成树(Prim算法)
算法思路
该问题本质是求解最小生成树(MST),需要连接所有村庄,使总费用最小。费用计算公式为:
费用 = √[(x₁-x₂)² + (y₁-y₂)²] + (h₁-h₂)²
其中:
- 前半部分为平面欧几里得距离(需开平方)
- 后半部分为高度差的平方
采用 Prim算法(适合稠密图),步骤:
- 从发电站(村庄0)开始初始化
- 每次选择当前距离生成树集合最近的未连接村庄
- 更新该村庄邻接点与集合的最小距离
- 重复直至所有村庄连通
C++代码实现
#include <iostream>
#include <vector>
#include <cmath>
#include <iomanip>
#include <climits>
using namespace std;struct Village {double x, y, h;
};double calculateCost(const Village& a, const Village& b) {double dx = a.x - b.x;double dy = a.y - b.y;double dh = a.h - b.h;return sqrt(dx*dx + dy*dy) + dh*dh; // 关键公式
}int main() {int n;cin >> n;vector<Village> villages(n);// 读取村庄数据for (int i = 0; i < n; ++i) {cin >> villages[i].x >> villages[i].y >> villages[i].h;}vector<double> minDist(n, 1e18); // 初始化为极大值vector<bool> visited(n, false);double totalCost = 0.0;// 从发电站(0号村庄)开始minDist[0] = 0;for (int i = 0; i < n; ++i) {int u = -1;// 寻找最近的未访问村庄for (int j = 0; j < n; ++j) {if (!visited[j] && (u == -1 || minDist[j] < minDist[u])) {u = j;}}if (minDist[u] == 1e18) { // 存在未连通村庄cout << "-1" << endl;return 0;}visited[u] = true;totalCost += minDist[u];// 更新邻接村庄的最小距离for (int v = 0; v < n; ++v) {if (!visited[v]) {double cost = calculateCost(villages[u], villages[v]);if (cost < minDist[v]) {minDist[v] = cost;}}}}cout << fixed << setprecision(2) << totalCost << endl;return 0;
}代码解析
-
数据结构
Village结构体存储坐标(x,y)和高度(h)minDist数组:记录各村庄到生成树集合的最小距离visited数组:标记村庄是否已连接
-
核心函数
double calculateCost(const Village& a, const Village& b) {double dx = a.x - b.x;double dy = a.y - b.y;double dh = a.h - b.h;return sqrt(dx*dx + dy*dy) + dh*dh; // 平面距离 + 高度差平方 } -
Prim算法流程
- 初始化:将发电站(0号村庄)距离设为0
- 贪心选择:每次选取
minDist最小的未访问村庄 - 更新距离:用新加入村庄更新邻接点距离
- 终止条件:所有村庄被访问
实例验证
输入样例:
4
1 1 3
9 9 7
8 8 6
4 5 4计算过程:
- 初始选择村庄0(1,1,3),距离集合为0
- 选择村庄3(4,5,4),费用=√(3²+4²)+(4-3)²=5+1=6
- 选择村庄2(8,8,6),费用=√(4²+3²)+(6-4)²=5+4=9
- 选择村庄1(9,9,7),费用=√(1²+1²)+(7-6)²≈1.41+1=2.41
- 总费用=6+9+2.41=17.41
输出结果:17.41 ✅
关键测试点
| 测试场景 | 预期结果 | 验证要点 |
|---|---|---|
| 单村庄 (n=1) | 0.00 | 边界条件处理 |
| 所有村庄高度相同 | 纯平面距离求和 | 高度计算正确性 |
| 所有村庄坐标相同 | 0.00 | 零距离处理 |
| 线性排列村庄 | 相邻距离求和 | 连接顺序正确性 |
| 高度差主导费用 | 优先选低高度差 | 贪心策略有效性 |
优化建议
-
堆优化Prim(时间复杂度O(ElogV))
priority_queue<pair<double, int>> pq; pq.push({0, 0}); while (!pq.empty()) {int u = pq.top().second;pq.pop();// ...更新邻接点距离并加入堆 } -
计算优化
- 预先计算所有点对距离 → 空间换时间(O(n²)空间)
- 高度差平方改用整数计算避免浮点误差
-
异常处理
- 添加连通性检查(未连通时返回-1)
- 浮点数精度控制(如用
1e-8容差)
注意事项
-
浮点精度问题
- 比较浮点数时使用容差:
abs(a-b) < 1e-8 - 输出时用
setprecision(2)控制小数位
- 比较浮点数时使用容差:
-
大数处理
- 坐标范围0~10000时,最大距离≈√(2×10000²)=14142,需用
double存储
- 坐标范围0~10000时,最大距离≈√(2×10000²)=14142,需用
-
算法选择
- 村庄数≤1000 → Prim的O(n²)优于Kruskal的O(n²logn)
- 若村庄数>10⁴,需改用堆优化Prim或Kruskal
相关文章:

[蓝桥杯]通电
通电 题目描述 2015 年,全中国实现了户户通电。作为一名电力建设者,小明正在帮助一带一路上的国家通电。 这一次,小明要帮助 nn 个村庄通电,其中 1 号村庄正好可以建立一个发电站,所发的电足够所有村庄使用。 现在…...

单片机0-10V电压输出电路分享
一、原理图 二、芯片介绍 GP8101是一个PWM信号转模拟信号转换器,相当于一个PWM信号输入,模拟信号输出的DAC。此 芯片可以将占空比为0%到100%的PWM信号线性转换成0-5V或者0-10V的模拟电压,并且输出电压 精度小于1%。GP8101M可以处理高频调制的…...

从零开始,搭建一个基于 Django 的 Web 项目
🎯 主要步骤概述 1️⃣ 安装 Python 和 pip 2️⃣ 创建虚拟环境 3️⃣ 安装 Django 4️⃣ 创建 Django 项目 5️⃣ 运行开发服务器 6️⃣ 创建一个简单的应用(app) 7️⃣ 配置数据库并迁移 8️⃣ 创建超级用户(admin)…...

大模型模型部署和暴露接口
创建环境 激活案件 安装相关依赖 conda create -n fastApi python3.10 conda activate fastApi conda install -c conda-forge fastapi uvicorn transformers pytorch pip install safetensors sentencepiece protobuf 新建文件夹 mkdir App cd App touch main.py 复制代码…...

2025服装收银系统推荐:智能管理助力服装商家高效经营
在服装批发零售行业,一套高效的收银系统不仅能简化日常经营流程,还能通过数据分析帮助商家优化库存、提升销售。随着AI技术的普及,现代收银系统已不再局限于简单的记账功能,而是能提供智能选品、库存预警、精准营销等进阶服务。 …...

Microsoft Copilot Studio - 尝试一下Agent
1.简单介绍 Microsoft Copilot Studio以前的名字是Power Virtual Agent(简称PVA)。Power Virutal Agent是2019年出现的,是低代码平台Power Platform的一部分。当时Generative AI还没有出现,但是基于已有的Conversation AI技术,即Microsoft L…...

【Python 算法零基础 4.排序 ⑨ 堆排序】
目录 一、问题描述 二、算法对比 1.朴素算法 ① 数组模拟容器 ② 有序数组模拟容器 2.二叉堆 ① 二叉堆特点 ② 数组表示二叉树 ③ 堆 ④ 大顶堆 ⑤ 小顶堆 ⑥ 元素插入 ⑦ 获取堆顶 ⑧ 堆顶元素删除 三、代码分析 1.工具函数 2.调整大顶堆函数 Ⅰ、计算子节点索引 Ⅱ、找出最…...

Deepseek/cherry studio中的Latex公式复制到word中
需要将Deepseek/cherry studio中公式复制到word中,但是deepseek输出Latex公式,比如以下Latex代码段,需要通过Mathtype翻译才能在word中编辑。 $$\begin{aligned}H_1(k1) & H_1(k) \frac{1}{A_1} \left( Q_1 u_1(k) Q_{i1} - Q_2 u_2(k…...

测试设计技术全解析:黑盒与白盒测试的七种武器与覆盖率指标
在软件开发的生命周期中,测试设计技术扮演着至关重要的角色,它直接影响着产品质量和用户体验。测试设计技术主要分为黑盒测试技术和白盒测试技术两大类,它们各有优势和适用场景。黑盒测试技术侧重于从用户视角验证软件功能是否符合需求&#…...
)
AWS中国区IAM相关凭证自行管理策略(只读CodeCommit版)
目标 需要从CodeCommit读取代码。除了设置AWS托管策略:AWSCodeCommitReadOnly。还需要自定义策略,让用户能够自行管理IAM自己的相关凭证。 IAM自定义策略 {"Version": "2012-10-17","Statement": [{"Sid": &…...

极限复习c++
一、核心语法必背 1. 指针 vs 引用(简答题高频) 区别指针引用定义存储地址的变量,可改指向变量的别名,绑定后不可改初始化可空(nullptr)、延迟初始化必须初始化,不能引用空值访问需解引用&…...
32单片机——窗口看门狗
1、WWDG的简介 WWDG:Window watchdog,即窗口看门狗 窗口看门狗本质上是能产生系统复位信号和提前唤醒中断的递减计数器 WWDG产生复位信号的条件: (1)当递减计数器值从0x40减到0x3F时复位(即T6位跳变到0&a…...

javascript中Cookie、BOM、DOM的使用
Cookie 在客户端存储小型文本数据(通常 ≤ 4KB),常用于会话管理、个性化设置等场景。 名称描述作用生命周期存储位置安全性会话 Cookie临时存储,浏览器关闭后自动删除会话管理、个性化设置浏览器关闭内存高持久 Cookie设置过期时…...

IDEA 中 Undo Commit,Revert Commit,Drop Commit区别
一、Undo Commit 适用情况:代码修改完了,已经Commit了,但是还未push,然后发现还有地方需要修改,但是又不想增加一个新的Commit记录。这时可以进行Undo Commit,修改后再重新Commit。如果已经进行了Push&…...

DAY43打卡
浙大疏锦行 kaggle找到一个图像数据集,用cnn网络进行训练并且用grad-cam做可视化 进阶:并拆分成多个文件 fruit_cnn_project/ ├─ data/ # 存放数据集(需手动创建,后续放入图片) │ ├─ train/ …...

Leetcode 1892. 页面推荐Ⅱ
1.题目基本信息 1.1.题目描述 表: Friendship ---------------------- | Column Name | Type | ---------------------- | user1_id | int | | user2_id | int | ---------------------- (user1_id,user2_id) 是 Friendship 表的主键(具有唯一值的列的组合…...

进程——环境变量及程序地址空间
目录 环境变量 概念 补充:命令行参数 引入 其它环境变量 理解 程序地址空间 引入 理解 虚拟地址存在意义 环境变量 概念 环境变量一般是指在操作系统中用来指定操作系统运行环境的一些参数。打个比方,就像你布置房间,这些参数就类…...
4 点李克特量表是什么)
(4-point Likert scale)4 点李克特量表是什么
文章目录 4-point Likert scale 定义4-point Likert scale 的构成4-point Likert scale 的特点4-point Likert scale 的应用场景 4-point Likert scale 定义 4-point Likert scale(4 点李克特量表)是一种常用的心理测量量表,由美国社会心理学…...

亚矩阵云手机实测体验:稳定流畅背后的技术逻辑
最近在测试一款云手机服务时,发现亚矩阵的表现出乎意料地稳定。作为一个经常需要多设备协作的开发者,我对云手机的性能、延迟和稳定性要求比较高。经过一段时间的体验,分享一下真实感受,避免大家踩坑。 1. 云手机能解决什么问…...

VR视频制作有哪些流程?
VR视频制作流程知识 VR视频制作,作为融合了创意与技术的复杂制作过程,涵盖从初步策划到最终呈现的多个环节。在这个过程中,我们可以结合众趣科技的产品,解析每一环节的实现与优化,揭示背后的奥秘。 VR视频制作有哪些…...

NodeJS全栈WEB3面试题——P2智能合约与 Solidity
2.1 简述 Solidity 的数据类型、作用域、函数修饰符。 数据类型: 值类型(Value Types):uint, int, bool, address, bytes1 到 bytes32, enum 引用类型(Reference Types):array, struct, mappin…...

某水表量每15分钟一报,然后某天示数清0了,重新报示值了 ,如何写sql 计算每日水量
要计算每日电量,需处理电表清零的情况。以下是针对不同数据库的解决方案: 方法思路 识别清零点:通过比较当前值与前一个值,若当前值明显变小(如小于前值的10%),则视为清零。分段累计ÿ…...

Ubuntu 系统部署 MySQL 入门篇
一、安装 MySQL 1.1 更新软件包 在终端中执行以下命令,更新系统软件包列表,确保安装的是最新版本的软件: sudo apt update 1.2 安装 MySQL 执行以下命令安装 MySQL 服务端: sudo apt install mysql-server 在安装过程中&…...

【MATLAB代码】制导——平行接近法,三维,目标是运动的,订阅专栏后可直接查看MATLAB源代码
文章目录 运行结果简介代码功能概述运行结果核心模块解析代码特性与优势MATLAB例程代码调整说明相关公式视线角速率约束相对运动学方程导引律加速度指令运动学更新方程拦截条件判定运行结果 运行演示视频: 三维平行接近法导引运行演示 简介 代码功能概述 本代码实现了三维空…...

大模型安全测试报告:千问、GPT 全系列、豆包、Claude 表现优异,DeepSeek、Grok-3 与 Kimi 存在安全隐患
大模型安全测试报告:千问、GPT 全系列、豆包、Claude 表现优异,DeepSeek、Grok-3 与 Kimi 存在安全隐患 引言 随着生成式人工智能技术的快速演进,大语言模型(LLM)正在广泛应用于企业服务、政务系统、教育平台、金融风…...

vue3 按钮级别权限控制
在Vue 3中实现按钮级别的权限控制,可以通过多种方式实现。这里我将介绍几种常见的方法: 方法1:使用Vue 3的Composition API 在Vue 3中,你可以使用Composition API来创建一个可复用的逻辑来处理权限控制。 创建权限控制逻辑 首…...

vue3子组件获取并修改父组件的值
在子组件中,父组件传递来的 prop 是只读的,但是确实有修改的需求,故此做个小小研究 // 父组件使用模版:update:xxx"dialogVisible $event" // 子组件使用模版 // const emits defineEmits([update:xxx]); // emits(u…...

【Redis】Cluster集群
目录 1、背景2、核心特性【1】数据分片【2】高可用【3】去中心化【4】客户端重定向 3、集群架构【1】最小规模【2】节点角色【3】通信协议 4、数据分片与路由【1】哈希槽分配【2】客户端路由逻辑 5、故障恢复6、适用场景 1、背景 Redis Cluster是Redis官方提供的分布式解决方案…...

黑马Java面试笔记之 微服务篇(SpringCloud)
一. SpringCloud 5大组件 SpringCloud 5大组件有哪些? 总结 五大件分别有: Eureka:注册中心Ribbon:负载均衡Feign:远程调用Hystrix:服务熔断Zuul/Gateway:网关 如果项目用到了阿里巴巴ÿ…...
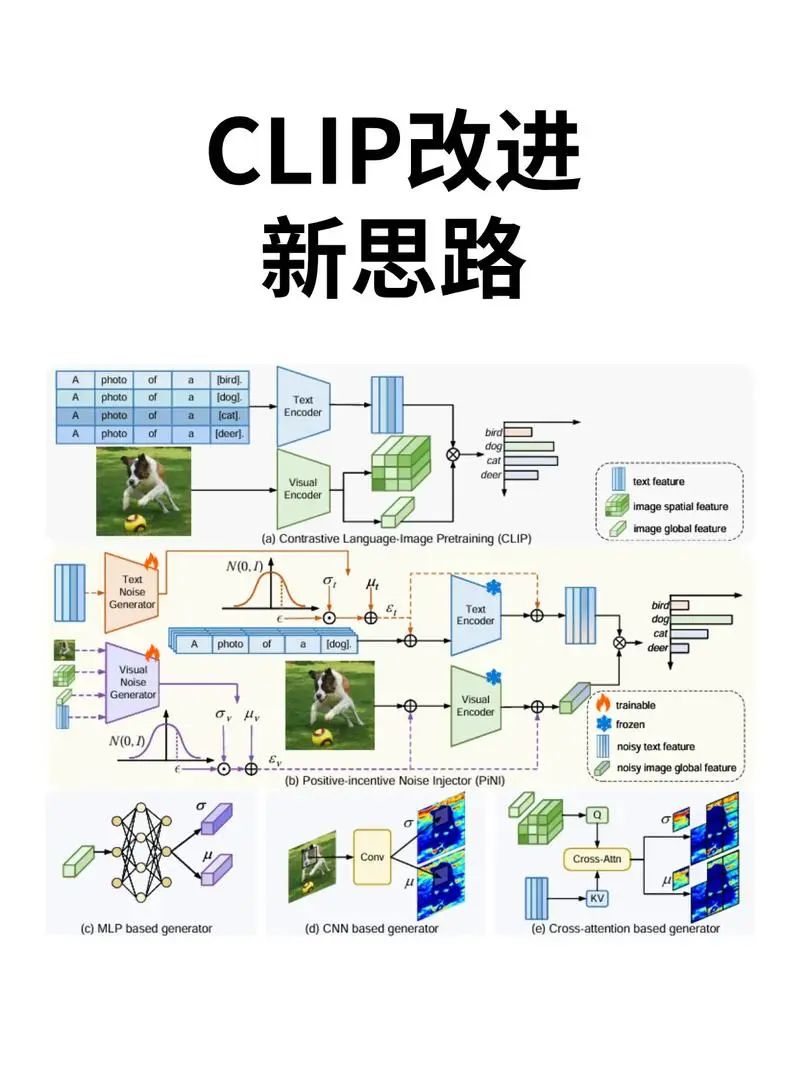
CLIP多模态大模型的优势及其在边缘计算中的应用
CLIP多模态大模型的优势及其在边缘计算中的应用 CLIP(Contrastive Language-Image Pre-training)模型,是OpenAI开发的一种多模态大模型。该模型通过对比学习的方式,在大规模图像-文本对上进行预训练,成功实现了图像和文…...
