平滑技术(数据处理,持续更新...)
一.介绍
“平滑”是一种用于减少数据中的短期波动、噪声或者异常值的技术,从而更清晰地揭示数据的长期趋势或周期性特征。
平滑的主要作用:
1.减少噪声。数据中常常包含各种随机噪声或误差,这些误差可能会掩盖数据的真实趋势。平滑可以降低噪声的影响,使数据更加平滑,更容易观察到数据的主要变化趋势。
2.揭示趋势。去除数据中的短期波动,使得长期趋势更加明显。对于理解数据的整体走向和进行长期预测非常重要。
3.数据可视化。平滑后的数据在图表中更容易呈现清晰的曲线或趋势线。
二.常见的平滑方法
-
移动平均(Moving Average, MA):
-
原理:计算数据窗口内的平均值,窗口向前移动一个数据点,重复计算。
-
适用场景:适用于短期趋势平滑,常用于金融时间序列分析。
-
公式:简单移动平均(SMA)公式为:
SMA_t = k分之一西格玛i从0到k-1对x_t-i求和其中,k 是窗口大小,xt−i 是时间序列数据。
-
-
加权移动平均(Weighted Moving Average, WMA):
-
原理:赋予不同位置的数据点不同的权重,通常较新的数据点赋予更大的权重。
-
适用场景:当数据的近期变化更重要时,如金融市场的短期预测。
-
公式:
WMAt=∑i=0k−1wi∑i=0k−1wixt−i其中,wi 是权重。
-
-
指数平滑(Exponential Smoothing, ES):
-
原理:赋予数据点递减的权重,越新的数据点权重越大,权重衰减呈指数形式。
-
适用场景:适用于具有趋势和季节性特征的数据。
-
公式:简单指数平滑(SES)公式为:
ESt=αxt+(1−α)ESt−1其中,α 是平滑参数,取值范围在 0 到 1 之间。
-
-
Hodrick-Prescott(HP)滤波:
-
原理:通过最小化趋势项和残差项的加权和,将时间序列分解为趋势项和周期项。
-
适用场景:常用于经济学中分离经济时间序列的趋势和周期成分。
-
-
Savitzky-Golay 滤波:
-
原理:通过对数据进行局部多项式拟合来平滑数据,保留数据的形状和特征。
-
适用场景:适用于需要保留数据细微特征的平滑处理,如光谱数据分析。
-
平滑的应用场景
-
金融数据分析:平滑股票价格、汇率等时间序列数据,帮助识别趋势和信号。
-
气象数据分析:平滑气温、降水量等气象数据,分析长期气候变化。
-
销售数据分析:平滑销售数据,预测未来销售趋势。
-
医学数据分析:平滑生理信号,如心电图(ECG)或脑电图(EEG)数据。
平滑的优缺点
-
优点:
-
去除噪声,揭示趋势。
-
提高数据可视化效果。
-
简单易实现,适用于多种数据类型。
-
-
缺点:
-
可能引入滞后性,影响实时性。
-
过度平滑可能丢失重要的短期信息。
-
例子:有下面的表格
| 时间 | 价格 |
| -- | --- |
| 1 | 100 |
| 2 | 102 |
| 3 | 98 |
| 4 | 101 |
| 5 | 103 |
| 6 | 105 |
| 7 | 106 |
| 8 | 104 |
| 9 | 102 |
| 10 | 100 |
我们使用简单移动平均(窗口大小为3)对数据进行平滑:
SMA3=3100+102+98=100 SMA4=3102+98+101=100.33S MA5=398+101+103=100.67
平滑后数据如下:
| 时间 | 价格 | SMA (3) |
| -- | --- | ------- |
| 1 | 100 | - |
| 2 | 102 | - |
| 3 | 98 | 100 |
| 4 | 101 | 100.33 |
| 5 | 103 | 100.67 |
| 6 | 105 | 103 |
| 7 | 106 | 104.67 |
| 8 | 104 | 105 |
| 9 | 102 | 104 |
| 10 | 100 | 102 |
三.应用
1.移动平均的应用1:填充缺失值
import numpy as npdef simple_moving_average_fill(data, window_size):"""使用简单移动平均填充缺失值参数:data: 包含缺失值的一维列表或数组window_size: 窗口大小(应为奇数)返回:填充后的数据数组"""data = np.array(data, dtype=np.float64)filled_data = data.copy()half_window = window_size // 2for i in range(len(data)):if np.isnan(data[i]):# 确定左侧和右侧的索引范围left = max(0, i - half_window)right = min(len(data), i + half_window + 1) # 加1是为了包含右侧边界,因为切片是左闭右开区间,而len(data)不加1是因为索引是从0开始的# 计算平均值时跳过NaN值window = data[left:right]non_nan_window = window[~np.isnan(window)] # np.isnan(window)返回布尔数组,~操作符取反,得到非NaN值的布尔索引if len(non_nan_window) > 0:filled_data[i] = np.mean(non_nan_window)else:filled_data[i] = np.nanreturn filled_data# 示例数据
data = [1.5, 2.3, np.nan, 4.1, np.nan, 5.2, 6.8, np.nan, 8.0]
filled_data = simple_moving_average_fill(data, window_size=3)print("原始数据:", data)
print("移动平均填充后的数据:", filled_data.tolist())
输出值:
原始数据: [1.5, 2.3, nan, 4.1, nan, 5.2, 6.8, nan, 8.0]
移动平均填充后的数据: [1.5, 2.3, 3.1999999999999997, 4.1, 4.65, 5.2, 6.8, 7.4, 8.0]
四.移动平均中对窗口的理解
在移动平均填充中,“窗口” 是指一组相邻的数据点,用于计算平均值。 以简单移动平均(SMA)为例,假设我们有一个时间序列数据集合,如 [1,2,3,4,5],我们选择一个窗口大小为 3。具体解释如下:
-
想象你是一个街边小店的老板,现在要分析每天经过你店门前的行人流量(这就是时间序列数据,代表不同时间点的数据),但某个时间段的数据因停电丢失了(即出现了缺失值),你希望用移动平均填充法来估算这些缺失值。
-
窗口大小 k 就好比你设定的一个“观察范围”。比如你选择窗口大小为 3,意味着你要根据缺失值前后共 3 天的数据(包括缺失值当天)来估算这个缺失值。
-
假设缺失值出现在第 3 天。你先向左看 1 天(即第 2 天)的数据,再向右看 1 天(即第 4 天)的数据,加上缺失值当天的位置(虽然数据缺失,但位置上还是算进去),一共 3 个数据点构成这个窗口。
-
当你用这个窗口内的数据来估算缺失值时,相当于综合了缺失值前后两天的行人流量,取一个平均值,作为缺失值的填充值。比如,如果第 2 天有 20 个人经过,第 4 天有 30 个人经过,那么缺失的第 3 天的行人流量估算值就是 (20+30)/2=25。
-
如果缺失值的位置靠近序列的开头或结尾,可能无法完整地找到两侧各 (k−1)/2 个数据点。这时你可以只用一侧的可用数据点来计算平均值,就像你开小店时,如果缺失的是前几天的数据,你只能参考后续几天的数据来估算一样。
五.pandas中的rolling函数:创建滚动窗口
pandas 中的 rolling() 函数用于创建滚动窗口计算(也称为移动窗口计算),它允许你在数据上定义一个固定大小的窗口,并在窗口滑动过程中对窗口内的数据进行统计操作(如均值、求和、标准差等)。这在时间序列分析、信号处理和金融数据分析中非常常见。
基本语法:
DataFrame.rolling(window, min_periods=None, center=False, win_type=None, on=None, axis=0, closed=None)-
window: 窗口大小(核心参数)-
整数:表示窗口包含的行数(如
window=3)。 -
时间字符串:用于时间序列(如
window='5D'表示 5 天)。
-
-
min_periods: 窗口内最少有效数据量(默认为window值)。 -
center: 是否以当前行为窗口中心(默认为False,窗口向右对齐)。 -
win_type: 窗口权重类型(如'hamming'、'gaussian')。 -
on: 对指定列应用滚动(仅适用于DataFrame)。 -
axis: 应用方向(0=行方向,1=列方向)
import pandas as pd
import numpy as npdata = {'value': [2, 5, 3, 8, 10, 7]}
df = pd.DataFrame(data)
# print(df)# 计算3个数据的滚动平均值
df['rolling_mean'] = df['value'].rolling(window=3).mean() # 参数center默认为False,表示滚动窗口向右偏移。设置为True时,滚动窗口会居中对齐
# print(df)# 只要窗口内有1个有效数据就计算
df['roll_min_periods'] = df['value'].rolling(window=3, min_periods=1).sum()
# print(df)# 窗口以当前行为中心
df['roll_center'] = df['value'].rolling(window=3, center=True).mean()
print(df)输出:
value rolling_mean roll_min_periods roll_center
0 2 NaN 2.0 NaN
1 5 NaN 7.0 3.333333
2 3 3.333333 10.0 5.333333
3 8 5.333333 16.0 7.000000
4 10 7.000000 21.0 8.333333
5 7 8.333333 25.0 NaN
# 时间序列滚动
# 创建时间序列数据
import pandas as pd
date_rng = pd.date_range(start='2023-01-01', periods=6, freq='D')
ts = pd.DataFrame({'value': [2, 5, 3, 8, 10, 7]}, index=date_rng)# 按3天窗口计算均值
ts['roll_time'] = ts['value'].rolling('3D').mean() # 默认min_periods=1,表示窗口内有1个有效数据就计算
print(ts)
# 这里没有前两行没有出现NaN值是因为滚动窗口是以时间为单位的,即时间窗口,min_periods默认值为1,表示只要窗口内有1个有效数据就计算均值
# 它与行数窗口不一样,行数窗口是以行数为单位的,即行数窗口,min_periods默认值为None,表示窗口内所有数据都有效才计算均值输出:
value roll_time
2023-01-01 2 2.000000
2023-01-02 5 3.500000
2023-01-03 3 3.333333
2023-01-04 8 5.333333
2023-01-05 10 7.000000
2023-01-06 7 8.333333
# 定义自定义函数(例如:计算窗口内最大值与最小值的差)
def max_min_diff(x):return x.max() - x.min()import pandas as pd
import numpy as np
data = {'value': [2, 5, 3, 8, 10, 7]}
df = pd.DataFrame(data)
df['custom'] = df['value'].rolling(3).apply(max_min_diff)
print(df)输出:
value custom
0 2 NaN
1 5 NaN
2 3 3.0
3 8 5.0
4 10 7.0
5 7 3.0
七.滚动时间窗口
在 Pandas 中,时间窗口(Time-based Window)是一种基于时间间隔而非固定行数的滚动计算方法,特别适合处理时间序列数据。与固定行数窗口不同,时间窗口能智能处理不规则时间间隔、缺失日期和真实时间边界。
基本语法
DataFrame.rolling(window, min_periods=1, center=False, win_type=None, closed=None)-
window(时间窗口大小)-
使用时间字符串定义窗口长度
-
格式:
'n' + 时间单位 -
常用单位:
-
'D'- 天 -
'H'- 小时 -
'T'或'min'- 分钟 -
'S'- 秒 -
'W'- 周 -
'M'- 月(注意:月不是固定天数) -
'Q'- 季度 -
'Y'- 年
-
-
-
min_periods(最小数据点要求)-
窗口内最少需要多少有效数据点才进行计算
-
默认值:1(只要有1个数据点就计算)
-
设置为窗口大小可强制要求完整数据
-
-
closed(窗口边界闭合规则)-
控制窗口边界是否包含:
-
'right':包含当前点,不包含左边界(默认) -
'left':包含左边界,不包含当前点 -
'both':包含两端 -
'neither':两端都不包含
-
-
对结果有重大影响,需根据业务场景选择
-
-
center(窗口居中)-
True:以当前点为中心 -
False:窗口在当前点结束(默认)
-
import pandas as pd
import numpy as np# 创建每日数据
dates = pd.date_range('2023-01-01', periods=5, freq='D')
values = [2, 5, 3, 8, 10]
ts = pd.DataFrame({'value': values}, index=dates)# 计算3天滚动平均值
ts['rolling_3D'] = ts['value'].rolling('3D').mean()print(ts)输出:
value rolling_3D
2023-01-01 2 2.000000 # 窗口:2023-01-01
2023-01-02 5 3.500000 # 窗口:2023-01-01 到 2023-01-02
2023-01-03 3 3.333333 # 窗口:2023-01-01 到 2023-01-03
2023-01-04 8 5.333333 # 窗口:2023-01-02 到 2023-01-04
2023-01-05 10 7.000000 # 窗口:2023-01-03 到 2023-01-05
# 创建不规则时间序列
irregular_dates = pd.DatetimeIndex(['2023-01-01 09:00','2023-01-01 09:02','2023-01-01 09:15','2023-01-01 09:30','2023-01-01 09:45'
])
values = [10, 15, 20, 18, 22]
irregular_ts = pd.DataFrame({'value': values}, index=irregular_dates)# 10分钟窗口计算均值
irregular_ts['10min_avg'] = irregular_ts['value'].rolling('10T').mean()print(irregular_ts)输出:
value 10min_avg
2023-01-01 09:00:00 10 10.000000 # 窗口:09:00-09:10 (仅09:00)
2023-01-01 09:02:00 15 12.500000 # 窗口:09:02-09:12 (09:00,09:02)
2023-01-01 09:15:00 20 20.000000 # 窗口:09:15-09:25 (仅09:15)
2023-01-01 09:30:00 18 18.000000 # 窗口:09:30-09:40 (仅09:30)
2023-01-01 09:45:00 22 22.000000 # 窗口:09:45-09:55 (仅09:45)
控制边界闭合规则
# 创建每分钟数据
minute_data = pd.DataFrame({'value': [10, 12, 15, 14, 18]},index=pd.date_range('2023-01-01 09:00', periods=5, freq='T')
)# 不同边界规则比较
minute_data['closed_right'] = minute_data['value'].rolling('2T', closed='right').mean()
minute_data['closed_left'] = minute_data['value'].rolling('2T', closed='left').mean()
minute_data['closed_both'] = minute_data['value'].rolling('2T', closed='both').mean()
minute_data['closed_neither'] = minute_data['value'].rolling('2T', closed='neither').mean()print(minute_data)输出
value closed_right closed_left closed_both closed_neither
2023-01-01 09:00:00 10 10.0 NaN 10.0 NaN
2023-01-01 09:01:00 12 11.0 10.0 11.0 10.0
2023-01-01 09:02:00 15 13.5 12.0 13.5 11.0
2023-01-01 09:03:00 14 14.5 15.0 14.5 13.5
2023-01-01 09:04:00 18 16.0 14.0 16.0 14.5
# 创建每日温度数据
temp_data = pd.DataFrame({'temp': [22, 24, 23, 25, 26, 28, 27]},index=pd.date_range('2023-06-01', periods=7, freq='D')
)# 居中3天窗口计算平均温度
temp_data['centered_3D'] = temp_data['temp'].rolling('3D', center=True).mean()print(temp_data)输出:
temp centered_3D
2023-06-01 22 NaN # 无法居中(左侧无数据)
2023-06-02 24 23.000000 # 窗口:06-01到06-03 → (22+24+23)/3
2023-06-03 23 24.000000 # 窗口:06-02到06-04 → (24+23+25)/3
2023-06-04 25 24.666667 # 窗口:06-03到06-05 → (23+25+26)/3
2023-06-05 26 26.333333 # 窗口:06-04到06-06 → (25+26+28)/3
2023-06-06 28 NaN # 无法居中(右侧无数据)
2023-06-07 27 NaN
复杂时间窗口应用
# 创建股票分钟数据
stock_data = pd.DataFrame({'price': [100, 101, 102, 103, 104, 105, 106],'volume': [5000, 6000, 5500, 7000, 8000, 7500, 9000]},index=pd.date_range('2023-01-01 09:30', periods=7, freq='5T')
)# 15分钟窗口计算技术指标
stock_data['15min_avg_price'] = stock_data['price'].rolling('15T').mean()
stock_data['15min_volume_sum'] = stock_data['volume'].rolling('15T').sum()
stock_data['15min_price_range'] = stock_data['price'].rolling('15T').apply(lambda x: x.max() - x.min())# 计算VWAP(成交量加权平均价)
def vwap_calc(x):prices = stock_data.loc[x.index, 'price']volumes = stock_data.loc[x.index, 'volume']return (prices * volumes).sum() / volumes.sum()stock_data['15min_VWAP'] = stock_data['price'].rolling('15T').apply(vwap_calc)print(stock_data)相关文章:
)
平滑技术(数据处理,持续更新...)
一.介绍 “平滑”是一种用于减少数据中的短期波动、噪声或者异常值的技术,从而更清晰地揭示数据的长期趋势或周期性特征。 平滑的主要作用: 1.减少噪声。数据中常常包含各种随机噪声或误差,这些误差可能会掩盖数据的真实趋势。平滑可以降低…...
)
App 上线后还能加固吗?iOS 应用的动态安全补强方案实战分享(含 Ipa Guard 等工具组合)
很多开发者以为 App 一旦上线,安全策略也就定型了。但现实是,App 上线只是攻击者的起点——从黑产扫描符号表、静态分析资源文件、注入调试逻辑,到篡改功能模块,这些行为都可能在你“以为很安全”的上线版本里悄然发生。 本篇文章…...
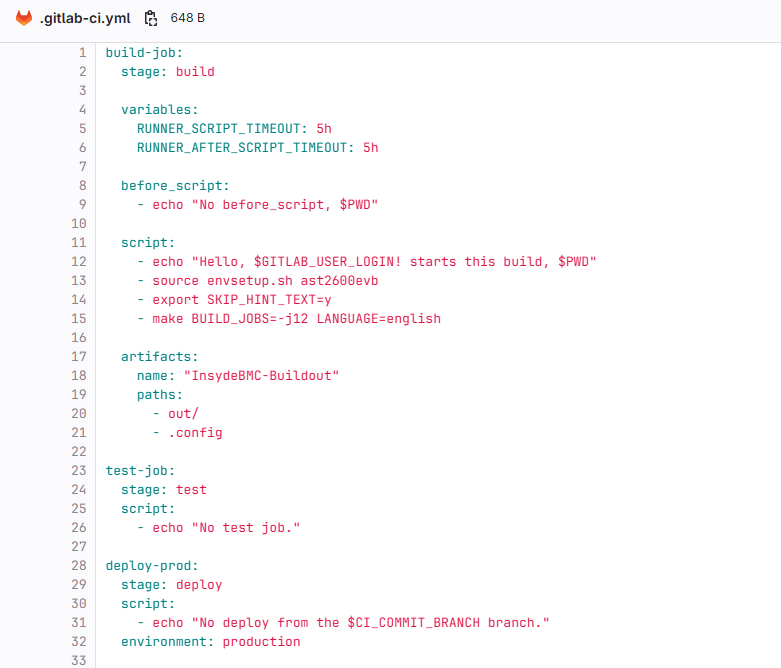
gitlab CI/CD本地部署配置
背景: 代码管理平台切换为公司本地服务器的gitlab server。为了保证commit的代码至少编译ok,也为了以后能拓展test cases,现在先搭建本地gitlab server的CI/CD基本的编译job pipeline。 配置步骤: 先安装gitlab-runner: curl -L "ht…...

AI大模型在测试领域应用案例拆解:AI赋能的软件测试效能跃迁的四大核心引擎(顺丰科技)
导语 5月份QECon深圳大会已经结束,继续更新一下案例拆解,本期是来自顺丰科技。 文末附完整版材料获取方式。 首先来看一下这个案例的核心内容,涵盖了测四用例设计、CI/CD辅助、测试执行、监控预警四大方面,也是算大家比较熟悉的…...

从零搭建uniapp项目
目录 创建uni-app项目 基础架构 安装 uni-ui 组件库 安装sass依赖 easycom配置组件自动导入 配置view等标签高亮声明 配置uni-ui组件类型声明 解决 标签 错误 关于tsconfig.json中提示报错 关于非原生标签错误(看运气) 安装 uview-plus 组件库…...

数据库密码加密
数据库密码加密 添加jar包构建工具类具体使用优缺点 添加jar包 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-security</artifactId> </dependency>构建工具类 public class PasswordUtil …...

GaLore:基于梯度低秩投影的大语言模型高效训练方法详解一
📘 GaLore:基于梯度低秩投影的大语言模型高效训练方法详解 一、论文背景与动机 随着大语言模型(LLM)参数规模的不断增长,例如 GPT-3(175B)、LLaMA(65B)、Qwenÿ…...

OpenCV CUDA模块图像处理------图像融合函数blendLinear()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 该函数执行 线性融合(加权平均) 两个图像 img1 和 img2,使用对应的权重图 weights1 和 weights2。 融合公式…...

Linux服务器如何安装wps?
1.到wps官网 https://www.wps.cn/product/wpslinux 2.到安装目录上执行命令 sudo dpkg -i wps-office*.deb 3.启动wps 在终端中输入 wps 命令即可启动 WPS...

图片压缩工具 | 图片生成PDF文档
OPEN-IMAGE-TINY,一个基于 Electron VUE3 的图片压缩工具,项目开源地址:https://github.com/0604hx/open-image-tiny ℹ️ 需求描述 上一版本发布后,有用户提出想要将图片转换(或者说生成更为贴切)PDF文档…...

Python的浅拷贝与深拷贝
一、浅拷贝 浅拷贝,指的是重新分配一块内存,创建一个新的对象,但里面的元素是原对象中各个子对象的引用。 浅拷贝有几种方法: 1、 使用数据类型本身的构造器 list1[1,2,3]list2 list(list1) # 使用了数据类型本身的构造器 list…...
VSCode - VSCode 放大与缩小代码
VSCode 放大与缩小代码 1、放大 点击顶部菜单栏【查看】 -> 点击外观 -> 点击【放大】 或者,使用快捷键:Ctrl # 操作方式先按住 Ctrl 键,再按 键2、缩小 点击顶部菜单栏【查看】 -> 点击外观 -> 点击【缩小】 或者&#x…...

消息队列处理模式:流式与批处理的艺术
🌊 消息队列处理模式:流式与批处理的艺术 📌 深入解析现代分布式系统中的数据处理范式 一、流式处理:实时数据的"活水" 在大数据时代,流式处理已成为实时分析的核心技术。它将数据视为无限的流,…...

11-Oracle 23ai Vector Embbeding和ONNX
Embedding (模型嵌入)是 AI 领域的一个核心概念 一、Embedding(嵌入)的含义 Embedding 是一种将 非结构化数据(如文本、图像、音频、视频)转换为 数值向量的技术。 其核心是通过 嵌入模型(…...
 序章)
Build a Large Language Model (From Scratch) 序章
关于本书 《从零构建大型语言模型》旨在帮助读者全面理解并从头创建类似GPT的大型语言模型(LLMs)。 全书首先聚焦于文本数据处理的基础知识和注意力机制的编码,随后指导读者逐步实现一个完整的GPT模型。书中还涵盖了预训练机制以及针对文本…...

【HarmonyOS 5】教育开发实践详解以及详细代码案例
以下是基于 HarmonyOS 5 的教育应用开发实践详解及核心代码案例,结合分布式能力与教育场景需求设计: 一、教育应用核心开发技术 ArkTS声明式UI 使用 State 管理学习进度状态,LocalStorageProp 实现跨页面数据同步(如课程…...

NoSQL 之Redis哨兵
目录 一、Redis 哨兵模式概述 (一)背景与核心目标 (二)基本架构组成 (三)核心功能 二、哨兵模式实现原理 (一)配置关键参数 (二)哨兵节点的定时任务 …...

【nano与Vim】常用命令
使用nano编辑器 保存文件 : 按下CtrlO组合键,然后按Enter键确认文件名。 退出编辑器 : 按下CtrlX组合键。 使用vi或vim编辑器 保存文件 : 按Esc键退出插入模式,然后输入:w并按Enter键保存文件。 退出编辑器 …...

OpenCV 图像色彩空间转换与抠图
一、知识点: 1、色彩空间转换函数 (1)、void cvtColor( InputArray src, OutputArray dst, int code, int dstCn 0, AlgorithmHint hint cv::ALGO_HINT_DEFAULT ); (2)、将图像从一种颜色空间转换为另一种。 (3)、参数说明: src: 输入图像,即要进行颜…...

Amazing晶焱科技:电子系统产品在多次静电放电测试后的退化案例
在我们的电子设计世界里,ESD(静电放电)问题总是让人头疼。尤其是当客户面临系统失效的困境时,寻找一个能够彻底解决问题的方案就变得格外重要。这一次,我们要谈的是一个经典案例:电子系统产品在多次静电放电…...

Go 中的 Map 与字符处理指南
Go 中的 Map 与字符处理指南 在 Go 中,map 可以存储字符,但需要理解字符在 Go 中的表示方式。在 Go 语言中,"字符" 实际上有两种表示方法:byte(ASCII 字符)和 rune(Unicode 字符&…...

互联网大厂Java求职面试:云原生架构下的微服务网关与可观测性设计
互联网大厂Java求职面试:云原生架构下的微服务网关与可观测性设计 郑薪苦怀着忐忑的心情走进了会议室,对面坐着的是某大厂的技术总监张总,一位在云原生领域有着深厚积累的专家。 第一轮面试:微服务网关的设计挑战 张总…...

C++中const关键字详解:不同情况下的使用方式
在 C 中,const 关键字用于指定一个对象或变量是常量,意味着它的值在初始化之后不能被修改。下面详细介绍 const 修饰变量、指针、类对象和类中成员函数的区别以及注意事项。 修饰变量 详细介绍 当 const 修饰变量时,该变量成为常量&#x…...

Java 2D 图形类总结与分类
一、基本形状类 这些类用于绘制简单的标准几何形状。 1. 圆形 / 椭圆类 Ellipse2D:椭圆基类,支持浮点精度。 子类: Ellipse2D.Double:双精度浮点坐标。Ellipse2D.Float:单精度浮点坐标。 参数:x, y, wid…...

C# 快速检测 PDF 是否加密,并验证正确密码
引言:为什么需要检测PDF加密状态? 在批量文档处理系统(如 OCR 文字识别、内容提取、格式转换)中,加密 PDF 无法直接操作。检测加密状态可提前筛选文件,避免流程因密码验证失败而中断。 本文使用 Free Spire…...

服务器信任质询
NSURLSession 与 NSURLAuthenticationMethodServerTrust —— 从零开始的“服务器信任质询”全流程 目标读者:刚接触 iOS 网络开发、准备理解 HTTPS 与证书校验细节的同学 出发点:搞清楚为什么会有“质询”、质询的触发时机、以及在 delegate 里怎么正确…...

华为云Flexus+DeepSeek征文| 华为云Flexus X实例单机部署Dify-LLM应用开发平台全流程指南
华为云FlexusDeepSeek征文| 华为云Flexus X实例单机部署Dify-LLM应用开发平台全流程指南 前言一、相关名词介绍1.1 华为云Flexus X实例介绍1.2 Dify介绍1.3 DeepSeek介绍1.4 华为云ModelArts Studio介绍 二、部署方案介绍2.1 方案介绍2.2 方案架构2.3 需要资源2.4 本…...

Python: 操作 Excel折叠
💡Python 操作 Excel 折叠(分组)功能详解(openpyxl & xlsxwriter 双方案) 在处理 Excel 报表或数据分析时,我们常常希望通过 折叠(分组)功能 来提升表格的可读性和组织性。本文将详细介绍如何使用 Python 中的两个主流 Excel 操作库 —— openpyxl 和 xlsxwriter …...

IBM官网新闻爬虫代码示例
通常我们使用Python编写爬虫,常用的库有requests(发送HTTP请求)和BeautifulSoup(解析HTML)。但这里需要注意的是,在爬取任何网站之前,务必遵守该网站的robots.txt文件和相关法律法规,…...

Java持久层技术对比:Hibernate、MyBatis与JPA的选择与应用
目录 简介持久层技术概述Hibernate详解MyBatis详解JPA详解技术选型对比最佳实践与应用场景性能优化策略未来发展趋势总结与建议 简介 在Java企业级应用开发中,持久层(Persistence Layer)作为连接业务逻辑与数据存储的桥梁,其技…...
