每日算法刷题Day25 6.7:leetcode二分答案3道题,用时1h40min(遇到两道动态规划和贪心时间较长)
3. 1631.最小体力消耗路径(中等,dfs不熟练)
1631. 最小体力消耗路径 - 力扣(LeetCode)
思想
1.你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ,其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ,且你希望去最右下角的格子 (rows-1, columns-1) (注意下标从 0 开始编号)。你每次可以往 上,下,左,右 四个方向之一移动,你想要找到耗费 体力 最小的一条路径。
一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。
请你返回从左上角走到右下角的最小 体力消耗值 。
2.单调性检验:二分答案的是体力消耗值(最大高度差绝对值),如果它越小,越不容易满足条件,所以有个最小值,而一旦一个值满足条件,大于它的值一定满足条件,符合单调性
3.dfs注意点:
(1)用vis数组记录已访问过的元素,避免重复反复,但是不要回溯
(2)dfs返回值是bool,这个用作判断条件,而不是直接return,避免找到一条可能路径就退出
if (dfs(heights, nx, ny, mid,vis)) { // 写判断条件而不是写return dfs(heights, nx, ny,// mid, vis),不然不会搜索其他路径return true;
}
代码
c++:
class Solution {
private:vector<int> dx = {-1, 1, 0, 0}, dy = {0, 0, -1, 1};public:bool inmap(int x, int y, int n, int m) {return 0 <= x && x < n && 0 <= y && y < m;}bool dfs(vector<vector<int>>& heights, int x, int y, int mid,vector<vector<bool>>& vis) {int n = heights.size(), m = heights[0].size();if (x == n - 1 && y == m - 1)return true;vis[x][y] = true; // 避免重复遍历for (int i = 0; i < 4; ++i) {int nx = x + dx[i], ny = y + dy[i];if (!inmap(nx, ny, n, m) || vis[nx][ny])continue;if (abs(heights[x][y] - heights[nx][ny]) <= mid) {if (dfs(heights, nx, ny, mid,vis)) { // 写判断条件而不是写return dfs(heights, nx, ny,// mid, vis),不然不会搜索其他路径return true;}}}// vis[x][y]=false; //不需要回溯return false;}bool check(vector<vector<int>>& heights, int mid) {int n = heights.size(), m = heights[0].size();vector<vector<bool>> vis(n, vector<bool>(m, false));if (dfs(heights, 0, 0, mid, vis))return true;elsereturn false;}int minimumEffortPath(vector<vector<int>>& heights) {check(heights, 2);int left = 0, right = INT_MIN, res = 0;for (int i = 0; i < heights.size(); ++i) {for (int j = 0; j < heights[0].size(); ++j) {if (j + 1 < heights[0].size())right = max(right, abs(heights[i][j + 1] - heights[i][j]));if (i + 1 < heights.size())right = max(right, abs(heights[i + 1][j] - heights[i][j]));}}while (left <= right) {int mid = left + ((right - left) >> 1);if (check(heights, mid)) {res = mid;right = mid - 1;} elseleft = mid + 1;}return res;}
};
4. 2560.打家劫舍IV(中等,学习动态规划和贪心证明)
2560. 打家劫舍 IV - 力扣(LeetCode)
思想
1.沿街有一排连续的房屋。每间房屋内都藏有一定的现金。现在有一位小偷计划从这些房屋中窃取现金。
由于相邻的房屋装有相互连通的防盗系统,所以小偷 不会窃取相邻的房屋 。
小偷的 窃取能力 定义为他在窃取过程中能从单间房屋中窃取的 最大金额 。
给你一个整数数组 nums 表示每间房屋存放的现金金额。形式上,从左起第 i 间房屋中放有 nums[i]美元。
另给你一个整数 k ,表示窃贼将会窃取的 最少 房屋数。小偷总能窃取至少 k 间房屋。
返回小偷的 最小 窃取能力。
2.单调性检验:二分答案是偷窃能力,偷窃能力越小,越不容易偷到k间房屋,所以存在一个最小值,而一旦一个值满足条件,大于它的值肯定满足条件,符合单调性
3.我的思路是dfs取搜索,但是会存在重复子问题(比如连续两个房屋都可以偷,但他们后面偷的房屋都一样,连续的第2个就要再求解重复子问题了),会超时,所以要用动态规划来消除冗余,解决重复子问题
4.学习动态规划:
- 状态定义:
f[i]表示到第i间房屋可以偷的房屋数量,所以最终答案是f[n-1] - 初始状态:如果
nums[0]<=mid,则f[0]=1,否则f[0]=0,f1为1的情况是n>1 && (nums[1]<=mid || f[0]=1) - 状态转移方程:
(1)nums[i]>mid,说明第i家不可以偷,f[i]=f[i-1]
(2)nums[i]<=mid,说明第i家可以偷,偷的话f[i]=f[i-2]+1,所以综上,f[i]=max(f[i-1],f[i-2]+1)(取最大的) - 遍历方式:i从2遍历到n-1即可
5.学习贪心
上式:
f[i]=max(f[i-1],f[i-2]+1)说明f[i]>=f[i-1],而f[i]至多比f[i-1]多1,所以f[i-1]+1>=f[i],即f[i-2]+1>=f[i-1],所以f[i]=f[i-2]+1,此式说明能偷则偷,最终答案是最大的
代码
c++:
我的dfs:
class Solution {
public:bool dfs(int x, vector<int>& nums, int k, int mid, int cnt) {if (cnt == k)return true;int n = nums.size();for (int i = x + 2; i < n; ++i) {if (nums[i] <= mid) {if (dfs(i, nums, k, mid, cnt + 1))return true;}}return false;}bool check(vector<int>& nums, int k, int mid) {int n = nums.size();int id = 0;for (int i = 0; i < n; ++i) {if (nums[i] <= mid) {id = i;break;}}if (dfs(id, nums, k, mid, 1) ||(id + 1 < n && nums[id + 1] <= mid && dfs(id + 1, nums, k, mid, 1)))return true;elsereturn false;}int minCapability(vector<int>& nums, int k) {int n = nums.size();int res = 0, left = INT_MAX, right = INT_MIN;for (const int x : nums) {left = min(left, x);right = max(right, x);}while (left <= right) {int mid = left + ((right - left) >> 1);if (check(nums, k, mid)) {res = mid;right = mid - 1;} elseleft = mid + 1;}return res;}
};
学习动态规划:
class Solution {
public:bool check(vector<int>& nums, int k, int mid) {int n = nums.size();vector<int> f(n, 0);if (nums[0] <= mid)f[0] = 1;// f[1]情况复杂一点if (n > 1 && (nums[1] <= mid || f[0] == 1))f[1] = 1;for (int i = 2; i < n; ++i) {f[i] = f[i - 1];if (nums[i] <= mid) {f[i] = max(f[i - 1], f[i - 2] + 1);}}if (f[n - 1] >= k)return true;elsereturn false;}int minCapability(vector<int>& nums, int k) {check(nums, k, 2);int n = nums.size();int res = 0, left = INT_MAX, right = INT_MIN;for (const int x : nums) {left = min(left, x);right = max(right, x);}while (left <= right) {int mid = left + ((right - left) >> 1);if (check(nums, k, mid)) {res = mid;right = mid - 1;} elseleft = mid + 1;}return res;}
};
学习贪心:
bool check(vector<int>& nums, int k, int mid) {int n = nums.size();int cnt = 0, i = 0;while (i < n) {if (nums[i] <= mid) {++cnt; // 能偷则偷if (cnt >= k)return true;i += 2;} else++i;}return false;
}
5. 2616.最小化数对的最大差值(中等,学习动态规划和贪心)
2616. 最小化数对的最大差值 - 力扣(LeetCode)
思想
1.给你一个下标从 0 开始的整数数组 nums 和一个整数 p 。请你从 nums 中找到 p 个下标对,每个下标对对应数值取差值,你需要使得这 p 个差值的 最大值 最小。同时,你需要确保每个下标在这 p 个下标对中最多出现一次。
对于一个下标对 i 和 j ,这一对的差值为 |nums[i] - nums[j]| ,其中 |x| 表示 x 的 绝对值 。
请你返回 p 个下标对对应数值 最大差值 的 最小值 。
2.单调性检验:二分答案的是最大差值,该值越小,越不能选择p个下标对,所以存在一个最小值,而一旦一个值成立,大于它的值一定满足条件
3.我想到先排序,但是无法证明就是选连续两个就是最优的,下面还是先写动态规划式子,然后能证明贪心最优
4.动态规划(与2560.打家劫舍IV一模一样):
- 状态定义:
f[i]在nums前i个数 中选择的最多有序对,所以答案为f[n-1] - 初始状态:
f[0]=0,f[1]=1的条件为n>1 && abs(nums[1]-nums[0]<=mid) - 状态转移方程:
(1)nums[i]与nums[i-1]不能选,即abs(nums[i]-nums[i-1])>mid,f[i]=f[i-1]
(2)nums[i]与nums[i-1]能选,即abs(nums[i]-nums[i-1])<=mid,f[i]=max(f[i-1],f[i-2]+1) - 遍历顺序:i从2开始到n-1
5.贪心证明:
f[i]=max(f[i-1],f[i-2]+1),而f[i-1]与f[i-2]最多差1,所以f[i-2]+1>=f[i-1],所以f[i]=f[i-2]+1,说明有连续两个满足条件就直接选择即可,满足贪心条件
代码
c++:
动态规划:
class Solution {
public:bool check(vector<int>& nums, int p, int mid) {int n = nums.size();vector<int> f(n, 0); // f[i]表示前i个元素中最多能选出的数对数f[0] = 0;if (n > 1 && abs(nums[1] - nums[0]) <= mid)f[1] = 1;for (int i = 2; i < n; ++i) {f[i] = f[i - 1];if (abs(nums[i] - nums[i - 1]) <= mid) {f[i] = max(f[i], f[i - 2] + 1);}}if (f[n - 1] >= p)return true;elsereturn false;}int minimizeMax(vector<int>& nums, int p) {int n = nums.size();int res = 0, left = 0, right = 0;sort(nums.begin(), nums.end());right = nums[n - 1] - nums[0];while (left <= right) {int mid = left + ((right - left) >> 1);if (check(nums, p, mid)) {res = mid;right = mid - 1;} elseleft = mid + 1;}return res;}
};
贪心:
bool check(vector<int>& nums, int p, int mid) {if (p == 0)return true;int n = nums.size();int cnt = 0;int i = 0;while (i + 1 < n) {if (abs(nums[i] - nums[i + 1]) <= mid) {++cnt;if (cnt >= p)return true;i += 2;} else++i;}return false;
}
相关文章:
)
每日算法刷题Day25 6.7:leetcode二分答案3道题,用时1h40min(遇到两道动态规划和贪心时间较长)
3. 1631.最小体力消耗路径(中等,dfs不熟练) 1631. 最小体力消耗路径 - 力扣(LeetCode) 思想 1.你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ,其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左…...

14-Oracle 23ai Vector Search 向量索引和混合索引-实操
一、Oracle 23ai支持的2种主要的向量索引类型: 1.1 内存中的邻居图向量索引 (In-Memory Neighbor Graph Vector Index) HNSW(Hierarchical Navigable Small World :分层可导航小世界)索引 是 Oracle AI Vector Search 中唯一支持的内存邻居图向量索引类…...

kubeadm安装k8s
1、环境准备 1.1、升级系统内核 参考另一篇文章:https://blog.csdn.net/u012533920/article/details/148457715?spm1011.2415.3001.5331 1.2、设置Hostname cat <<EOF > /etc/hosts 127.0.0.1 localhost localhost.localdomain localhost4 localhos…...

服务器新建用户无法使用conda
服务器新建用户无法使用conda 1.将.bashrc文件复制到新用户家目录下 sudo cp .bashrc /home/newuser/.bashrc2.source命令激活该文件 source ~/.bashrc3.将.condarc文件复制到新用户家目录下 sudo cp .condarc/home/newuser/.condarc...

Web前端基础:JavaScript
1.JS核心语法 1.1 JS引入方式 第一种方式:内部脚本,将JS代码定义在HTML页面中 JavaScript代码必须位于<script></script>标签之间在HTML文档中,可以在任意地方,放置任意数量的<script></script>一般会把…...

基于对比学习的带钢表面缺陷分类研究,整合SimCLR自监督预训练与YOLOv8目标检测框架的技术解析及Python实现方案
以下基于对比学习的带钢表面缺陷分类研究,整合SimCLR自监督预训练与YOLOv8目标检测框架的技术解析及Python实现方案: 基于对比学习的带钢表面缺陷分类研究 ——SimCLR与YOLOv8算法融合应用 #mermaid-svg-VqDPIOfR5WJcGtD7 {font-family:"trebuchet ms",verdana,ar…...

基于AWS Serverless架构:零运维构建自动化SEO内容生成系统
作者:[Allen] 技术专栏 | 深度解析云原生SEO自动化 在流量为王的时代,持续产出高质量SEO内容成为技术运营的核心痛点。传统方案面临开发成本高、扩展性差、关键词响应滞后三大难题。本文将分享如何用AWS Serverless技术栈,构建一套零服务器运…...
)
【.net core】天地图坐标转换为高德地图坐标(WGS84 坐标转 GCJ02 坐标)
类文件 public static class WGS84ToGCJ02Helper {// 定义一些常量private const double PI 3.14159265358979324;private const double A 6378245.0;private const double EE 0.00669342162296594323;// 判断坐标是否在中国范围内(不在国内则不进行转换&#x…...

Linux操作系统故障应急场景及对应排查方法
001:系统CPU负载高并触发监控报警 005 查看系统CPU使用情况,,确认CPU数量,确认系统负载,确认CPU高对系统的影响 006 定位占用CPU资源最多的进程,根据进程判断是应用进程还是系统进程还是第三方工具进程。 014 查看…...

电镀机的阳极是什么材质?
知识星球(星球名:芯片制造与封测技术社区,点击加入)里的学员问:电镀的阳极有什么讲究?什么是可溶性阳极和非可溶性阳极? 什么是可溶性阳极与非可溶性阳极? 可溶性阳极 阳极本身就是…...

vscode调试deepspeed的方法之一(无需调整脚本)
现在deepspeed的脚本文件是: # 因为使用 RTX 4000 系列显卡时,不支持通过 P2P 或 IB 实现更快的通信宽带,需要设置以下两个环境变量 # 禁用 NCCL 的 P2P 通信,以避免可能出现的兼容性问题 export NCCL_P2P_DISABLE"1" …...

神经网络-Day44
import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pyplot as plt# 设置中文字体支持 plt.rcParams["font.family"] ["SimHei"…...

创客匠人:如何通过精准定位实现创始人IP打造与知识变现
在当今知识经济时代,越来越多的专业人士希望通过个人品牌实现知识变现,但许多人面临一个共同困境:明明很努力,却收效甚微。创客匠人作为深耕知识付费赛道9年的专业机构,揭示了这一现象背后的关键原因——90%的IP失败源…...

Codeforces Round 509 (Div. 2) C. Coffee Break
题目大意: 给你n、m、d n为元素个数,m为数列长度,d为每个元素之间的最短间隔 问最少需要多少个数列可以使得元素都能装进数列,并且满足每个元素之间的间隔大于等于d 核心思想 使用贪心的思想,将元素的大小进行排序,问题出在必…...
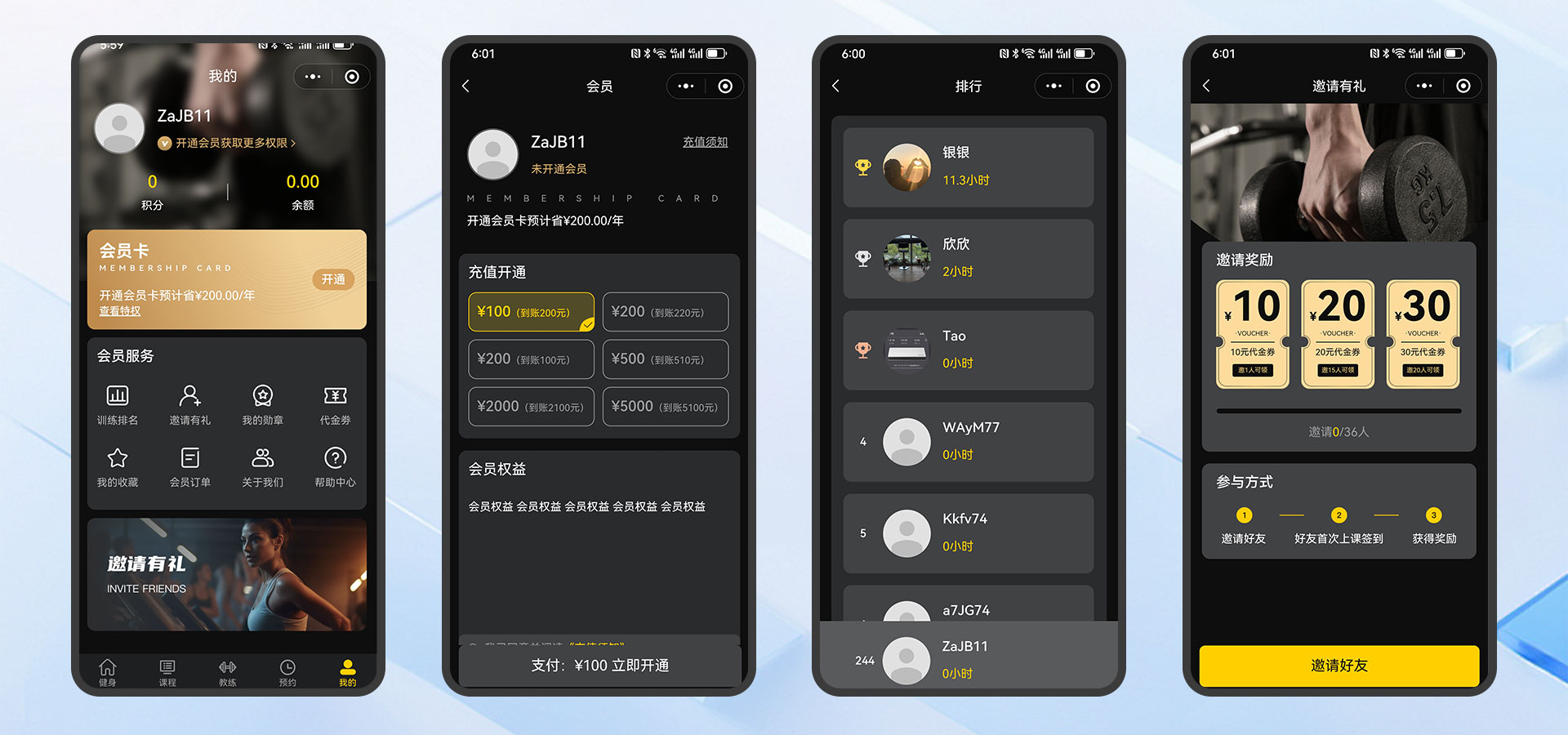
榕壹云健身预约系统:多门店管理的数字化解决方案(ThinkPHP+MySQL+UniApp实现)
随着全民健身热潮的兴起,传统健身房在会员管理、课程预约、多门店运营等方面面临诸多挑战。针对这一需求,我们开发了一款基于ThinkPHPMySQLUniApp的榕壹云健身预约系统,为中小型健身机构及连锁品牌提供高效、灵活的数字化管理工具。本文将详细…...

QUIC——UDP实现可靠性传输
首先我们要知道TCP存在什么样的痛点问题 TCP的升级很困难TCP建立连接的延迟网络迁移需要重新建立连接TCP存在队头阻塞问题 QUIC就是为了解决以上的问题而诞生了, 下面我会介绍QUIC的一些特性和原理 QUIC对比TCP优势: 握手建连更快 QUIC内部包含了TLS, 它在自己的帧会携带TL…...

提高Python编程效率的工具推荐
在 Python 开发中,选择合适的工具可以显著提升编程效率。以下是一些经过精心挑选的工具,涵盖代码编辑、调试、数据分析等多个方面,希望能帮助你在 Python 开发中事半功倍。 一、集成开发环境(IDE) 1. PyCharm PyCha…...

React Native图片预加载:让你的应用图片预览像德芙一样丝滑
写在前面:一张图片引发的性能血案 你有没有遇到过这种情况?——用户疯狂滑动你的React Native图片列表,结果图片加载慢得像蜗牛,甚至出现空白闪烁?等到图片终于加载出来,用户早就失去耐心,愤然退出…… 但你知道吗?这个问题只需要几行代码就能解决! 比如,使用reac…...

快速上手shell脚本运行流程控制
一、条件运行流程控制 1.if单分支结构 #!/bin/bash if [ 条件 ] then动作1动作2... fi 2.if双分支结构 #!/bin/bash if [ 条件 ] then动作1动作2... else动作1动作2... fi 3.if多分支结构 二、循环运行流程控制 1.无判定for循环 给网卡一键添加5个IP 2.判断循环 while…...

10.Linux进程信号
1. 理解信号 信号VS信号量 老婆:老婆饼-》没有任何关系!信号:闹钟,上课铃声,脸色...人-》进程;信号中断人正在做的事,是一种事件的异步通知机制; 我们自习一会,等张三回…...

Python 函数全攻略:函数基础
函数(Functions)基础 什么是函数? 一个命名的代码块,代指一大堆代码。 定义: def function_name(): (使用def关键字,英文括号,冒号,缩进代码块)。 执行/调用: function…...

机器学习基础(四) 决策树
决策树简介 决策树结构: 决策树是一种树形结构,树中每个内部节点表示一个特征上的判断,每个分支代表一个判断结果的输出,每个叶子节点代表一种分类结果 决策树构建过程(三要素): 特征选择 选…...

DDPM优化目标公式推导
DDPM优化目标公式推导 DDPM优化目标公式推导**1. 问题定义****2. 优化目标:最大化对数似然****3. 变分下界的分解****4. 关键步骤:简化 KL 散度项****(a) 后验分布 q ( x t − 1 ∣ x t , x 0 ) q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0) q(xt…...
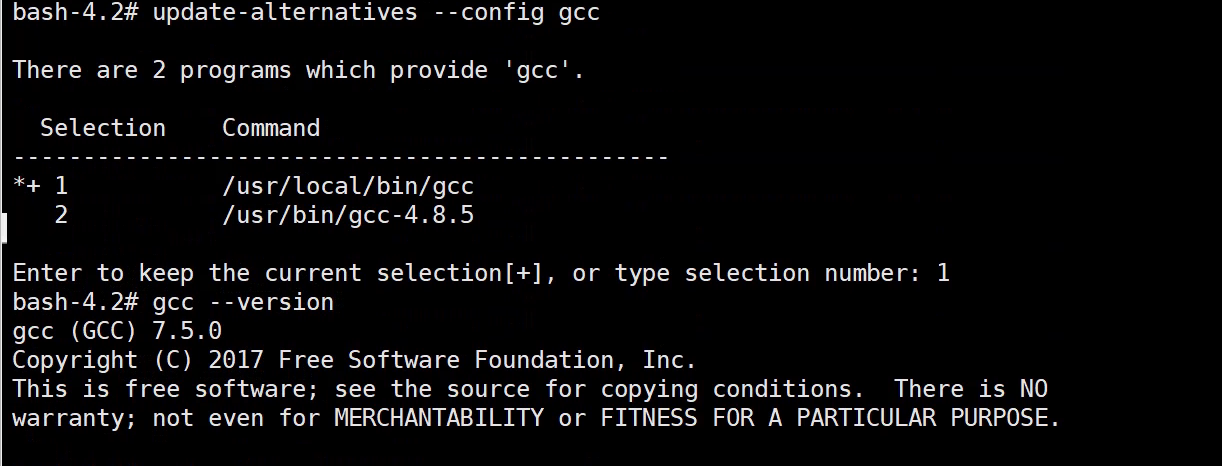
CentOS 7如何编译安装升级gcc至7.5版本?
CentOS 7如何编译安装升级gcc版本? 由于配置CentOS-SCLo-scl.repo与CentOS-SCLo-scl-rh.repo后执行yum install -y devtoolset-7安装总是异常,遂决定编译安装gcc7.5 # 备份之前的yum .repo文件至 /tmp/repo_bak 目录 mkdir -p /tmp/repo_bak && cd /etc…...

为什么React列表项需要key?(React key)(稳定的唯一标识key有助于React虚拟DOM优化重绘大型列表)
文章目录 1. **帮助 React 识别列表项的变化**2. **性能优化**3. **避免组件状态混乱**4. **为什么使用 rpid 作为 key**5. **不好的做法示例**6. **✅ 正确的做法** 在 React 中添加 key{item.rpid} 是非常重要的,主要有以下几个原因: 1. 帮助 React 识…...
)
Playwright自动化测试全栈指南:从基础到企业级实践(2025终极版)
引言 在Web应用复杂度指数级增长的今天,传统自动化测试工具面临动态渲染适配难、多浏览器兼容差、测试稳定性低三大挑战。微软开源的Playwright凭借跨浏览器支持、自动等待机制和原生异步架构,成为新一代自动化测试的事实标…...

飞牛云一键设置动态域名+ipv6内网直通访问内网的ssh服务-家庭云计算专家
IPv6访问SSH的难点与优势并存。难点主要体现在网络环境支持不足:部分ISP未完全适配IPv6协议,导致客户端无法直接连通;老旧设备或工具(如Docker、GitHub)需额外配置才能兼容IPv6,技术门槛较高;若…...

虚实共生时代的情感重构:AI 恋爱陪伴的崛起、困局与明日图景
一、虚拟恋人:从技术幻想到情感刚需的跨越 在 5G 网络编织的数字浪潮里,AI 驱动的虚拟恋人正打破次元界限。深度学习算法剖析 3000 万段真实对话语料库,搭配 VR 设备带来的多维度交互体验,如今的虚拟对象已能精准模拟瞳孔微表情&…...
!!!C++语言(嵌入式八股文,嵌入式面经))
嵌入式面试高频(5)!!!C++语言(嵌入式八股文,嵌入式面经)
一、C有几种传值方式之间的区别 一、值传递(Pass by Value) 机制:创建参数的副本,函数内操作不影响原始数据语法:void func(int x)特点: 数据安全:原始数据不受影响性能开销:需要复…...

C++动态规划-线性DP
这是一套C线性DP题目的答案。如果需要题目,请私信我,我将会更新题干 P1:单子序列最大和 #include <bits/stdc.h> using namespace std; int n,A,B,C; int a[200005]; int s[200005]; int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)…...
