DDPM优化目标公式推导
DDPM优化目标公式推导
- DDPM优化目标公式推导
- **1. 问题定义**
- **2. 优化目标:最大化对数似然**
- **3. 变分下界的分解**
- **4. 关键步骤:简化 KL 散度项**
- **5. 最终优化目标**
- **关键结论**
- 补充内容(优化思路)
- 变分下界(VLB)最终简化公式的逐项解析与优化思路
- **1. 重构项 (Reconstruction Term)**
- **2. 去噪匹配项 (Denoising Matching Term)**
- **3. 先验匹配项 (Prior Matching Term)**
- **整体优化思路分析**
- **1. 核心优化目标**
- **2. 实际训练简化**
- **3. 物理意义图解**
- **4. 为什么此优化有效?**
- **总结**
DDPM优化目标公式推导
DDPM(Denoising Diffusion Probabilistic Models)的优化目标推导基于变分下界(Variational Lower Bound, VLB) 或 证据下界(Evidence Lower Bound, ELBO)。以下是详细推导过程:
1. 问题定义
- 目标:学习一个模型 p θ ( x 0 ) p_\theta(\mathbf{x}_0) pθ(x0) 逼近真实数据分布 q ( x 0 ) q(\mathbf{x}_0) q(x0)。
- 前向过程(扩散过程):
固定方差序列 β 1 , … , β T \beta_1, \dots, \beta_T β1,…,βT,定义马尔可夫链:
q ( x 1 : T ∣ x 0 ) = ∏ t = 1 T q ( x t ∣ x t − 1 ) , q ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t x t − 1 , β t I ) q(\mathbf{x}_{1:T} | \mathbf{x}_0) = \prod_{t=1}^T q(\mathbf{x}_t | \mathbf{x}_{t-1}), \quad q(\mathbf{x}_t | \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t \mathbf{I}) q(x1:T∣x0)=t=1∏Tq(xt∣xt−1),q(xt∣xt−1)=N(xt;1−βtxt−1,βtI) - 反向过程(生成过程):
学习参数化的马尔可夫链:
p θ ( x 0 : T ) = p ( x T ) ∏ t = 1 T p θ ( x t − 1 ∣ x t ) , p θ ( x t − 1 ∣ x t ) = N ( x t − 1 ; μ θ ( x t , t ) , Σ θ ( x t , t ) ) p_\theta(\mathbf{x}_{0:T}) = p(\mathbf{x}_T) \prod_{t=1}^T p_\theta(\mathbf{x}_{t-1} | \mathbf{x}_t), \quad p_\theta(\mathbf{x}_{t-1} | \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t)) pθ(x0:T)=p(xT)t=1∏Tpθ(xt−1∣xt),pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))
2. 优化目标:最大化对数似然
目标是最大化 log p θ ( x 0 ) \log p_\theta(\mathbf{x}_0) logpθ(x0),但直接计算困难,转而最大化其变分下界:
log p θ ( x 0 ) ≥ E q ( x 1 : T ∣ x 0 ) [ log p θ ( x 0 : T ) q ( x 1 : T ∣ x 0 ) ] ≜ VLB \log p_\theta(\mathbf{x}_0) \geq \mathbb{E}_{q(\mathbf{x}_{1:T} | \mathbf{x}_0)} \left[ \log \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} | \mathbf{x}_0)} \right] \triangleq \text{VLB} logpθ(x0)≥Eq(x1:T∣x0)[logq(x1:T∣x0)pθ(x0:T)]≜VLB
3. 变分下界的分解
将 VLB 展开并分解:
VLB = E q ( x 1 : T ∣ x 0 ) [ log p θ ( x 0 : T ) q ( x 1 : T ∣ x 0 ) ] = E q [ log p θ ( x 0 : T ) q ( x 1 : T ∣ x 0 ) ] = E q [ log p θ ( x T ) + ∑ t = 1 T log p θ ( x t − 1 ∣ x t ) q ( x t ∣ x t − 1 ) ] \begin{align*} \text{VLB} &= \mathbb{E}_{q(\mathbf{x}_{1:T} | \mathbf{x}_0)} \left[ \log \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} | \mathbf{x}_0)} \right] \\ &= \mathbb{E}_{q} \left[ \log \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} | \mathbf{x}_0)} \right] \\ &= \mathbb{E}_{q} \left[ \log p_\theta(\mathbf{x}_T) + \sum_{t=1}^T \log \frac{p_\theta(\mathbf{x}_{t-1} | \mathbf{x}_t)}{q(\mathbf{x}_t | \mathbf{x}_{t-1})} \right] \\ \end{align*} VLB=Eq(x1:T∣x0)[logq(x1:T∣x0)pθ(x0:T)]=Eq[logq(x1:T∣x0)pθ(x0:T)]=Eq[logpθ(xT)+t=1∑Tlogq(xt∣xt−1)pθ(xt−1∣xt)]
利用马尔可夫性质,改写为:
VLB = E q [ log p θ ( x 0 ∣ x 1 ) + ∑ t = 2 T log p θ ( x t − 1 ∣ x t ) q ( x t − 1 ∣ x t , x 0 ) − ∑ t = 1 T log q ( x t ∣ x t − 1 ) q ( x t − 1 ∣ x 0 ) ] + C \text{VLB} = \mathbb{E}_{q} \left[ \log p_\theta(\mathbf{x}_0 | \mathbf{x}_1) + \sum_{t=2}^T \log \frac{p_\theta(\mathbf{x}_{t-1} | \mathbf{x}_t)}{q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0)} - \sum_{t=1}^T \log \frac{q(\mathbf{x}_t | \mathbf{x}_{t-1})}{q(\mathbf{x}_{t-1} | \mathbf{x}_0)} \right] + C VLB=Eq[logpθ(x0∣x1)+t=2∑Tlogq(xt−1∣xt,x0)pθ(xt−1∣xt)−t=1∑Tlogq(xt−1∣x0)q(xt∣xt−1)]+C
最终简化为:
VLB = E q [ log p θ ( x 0 ∣ x 1 ) ] − ∑ t = 2 T E q [ D KL ( q ( x t − 1 ∣ x t , x 0 ) ∥ p θ ( x t − 1 ∣ x t ) ) ] − D KL ( q ( x T ∣ x 0 ) ∥ p ( x T ) ) \boxed{\text{VLB} = \mathbb{E}_{q} \left[ \log p_\theta(\mathbf{x}_0 | \mathbf{x}_1) \right] - \sum_{t=2}^T \mathbb{E}_{q} \left[ D_\text{KL} \left( q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_{t-1} | \mathbf{x}_t) \right) \right] - D_\text{KL} \left( q(\mathbf{x}_T | \mathbf{x}_0) \parallel p(\mathbf{x}_T) \right)} VLB=Eq[logpθ(x0∣x1)]−t=2∑TEq[DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))]−DKL(q(xT∣x0)∥p(xT))
详细过程请参考DDPM优化目标公式推导(详细)
4. 关键步骤:简化 KL 散度项
(a) 后验分布 q ( x t − 1 ∣ x t , x 0 ) q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0) q(xt−1∣xt,x0) 的闭式解
由贝叶斯公式:
q ( x t − 1 ∣ x t , x 0 ) = N ( x t − 1 ; μ ~ t ( x t , x 0 ) , β ~ t I ) q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0), \tilde{\beta}_t \mathbf{I}) q(xt−1∣xt,x0)=N(xt−1;μ~t(xt,x0),β~tI)
其中:
μ ~ t ( x t , x 0 ) = α ˉ t − 1 β t 1 − α ˉ t x 0 + α t ( 1 − α ˉ t − 1 ) 1 − α ˉ t x t , β ~ t = 1 − α ˉ t − 1 1 − α ˉ t β t \tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0) = \frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1 - \bar{\alpha}_t} \mathbf{x}_0 + \frac{\sqrt{\alpha_t} (1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t, \quad \tilde{\beta}_t = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t μ~t(xt,x0)=1−αˉtαˉt−1βtx0+1−αˉtαt(1−αˉt−1)xt,β~t=1−αˉt1−αˉt−1βt
(记 α t = 1 − β t \alpha_t = 1 - \beta_t αt=1−βt, α ˉ t = ∏ i = 1 t α i \bar{\alpha}_t = \prod_{i=1}^t \alpha_i αˉt=∏i=1tαi)
(b) 参数化均值 μ θ ( x t , t ) \boldsymbol{\mu}_\theta(\mathbf{x}_t, t) μθ(xt,t)
设 p θ ( x t − 1 ∣ x t ) = N ( x t − 1 ; μ θ ( x t , t ) , Σ θ ( x t , t ) ) p_\theta(\mathbf{x}_{t-1} | \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t)) pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))。
为匹配后验分布,选择:
μ θ ( x t , t ) = μ ~ t ( x t , x t − 1 − α ˉ t ϵ θ α ˉ t ) \boldsymbol{\mu}_\theta(\mathbf{x}_t, t) = \tilde{\boldsymbol{\mu}}_t \left( \mathbf{x}_t, \frac{\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t} \boldsymbol{\epsilon}_\theta}{\sqrt{\bar{\alpha}_t}} \right) μθ(xt,t)=μ~t(xt,αˉtxt−1−αˉtϵθ)
代入闭式解得:
μ θ = 1 α t ( x t − β t 1 − α ˉ t ϵ θ ( x t , t ) ) \boldsymbol{\mu}_\theta = \frac{1}{\sqrt{\alpha_t}} \left( \mathbf{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \right) μθ=αt1(xt−1−αˉtβtϵθ(xt,t))
© KL 散度的闭式解
两个高斯分布的 KL 散度为:
D KL ( N ( μ 1 , Σ 1 ) ∥ N ( μ 2 , Σ 2 ) ) = 1 2 [ log ∣ Σ 2 ∣ ∣ Σ 1 ∣ − d + tr ( Σ 2 − 1 Σ 1 ) + ( μ 2 − μ 1 ) ⊤ Σ 2 − 1 ( μ 2 − μ 1 ) ] D_\text{KL}(\mathcal{N}(\boldsymbol{\mu}_1, \boldsymbol{\Sigma}_1) \parallel \mathcal{N}(\boldsymbol{\mu}_2, \boldsymbol{\Sigma}_2)) = \frac{1}{2} \left[ \log \frac{|\boldsymbol{\Sigma}_2|}{|\boldsymbol{\Sigma}_1|} - d + \text{tr}(\boldsymbol{\Sigma}_2^{-1} \boldsymbol{\Sigma}_1) + (\boldsymbol{\mu}_2 - \boldsymbol{\mu}_1)^\top \boldsymbol{\Sigma}_2^{-1} (\boldsymbol{\mu}_2 - \boldsymbol{\mu}_1) \right] DKL(N(μ1,Σ1)∥N(μ2,Σ2))=21[log∣Σ1∣∣Σ2∣−d+tr(Σ2−1Σ1)+(μ2−μ1)⊤Σ2−1(μ2−μ1)]
假设 Σ θ = σ t 2 I \boldsymbol{\Sigma}_\theta = \sigma_t^2 \mathbf{I} Σθ=σt2I(常取 σ t 2 = β t \sigma_t^2 = \beta_t σt2=βt 或 β ~ t \tilde{\beta}_t β~t),则:
D KL = 1 2 σ t 2 ∥ μ ~ t − μ θ ∥ 2 + C D_\text{KL} = \frac{1}{2\sigma_t^2} \| \tilde{\boldsymbol{\mu}}_t - \boldsymbol{\mu}_\theta \|^2 + C DKL=2σt21∥μ~t−μθ∥2+C
代入 μ θ \boldsymbol{\mu}_\theta μθ 和 μ ~ t \tilde{\boldsymbol{\mu}}_t μ~t 的表达式:
μ ~ t − μ θ = β t α t 1 − α ˉ t ( ϵ − ϵ θ ( x t , t ) ) \tilde{\boldsymbol{\mu}}_t - \boldsymbol{\mu}_\theta = \frac{\beta_t}{\sqrt{\alpha_t} \sqrt{1 - \bar{\alpha}_t}} \left( \boldsymbol{\epsilon} - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \right) μ~t−μθ=αt1−αˉtβt(ϵ−ϵθ(xt,t))
其中 x t = α ˉ t x 0 + 1 − α ˉ t ϵ \mathbf{x}_t = \sqrt{\bar{\alpha}_t} \mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t} \boldsymbol{\epsilon} xt=αˉtx0+1−αˉtϵ。最终:
D KL ∝ E x 0 , ϵ [ ∥ ϵ − ϵ θ ( x t , t ) ∥ 2 ] \boxed{D_\text{KL} \propto \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \left[ \| \boldsymbol{\epsilon} - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \|^2 \right]} DKL∝Ex0,ϵ[∥ϵ−ϵθ(xt,t)∥2]
5. 最终优化目标
忽略常数项和权重,DDPM 的简化目标为:
L simple ( θ ) = E t , x 0 , ϵ [ ∥ ϵ − ϵ θ ( x t , t ) ∥ 2 ] \mathcal{L}_\text{simple}(\theta) = \mathbb{E}_{t, \mathbf{x}_0, \boldsymbol{\epsilon}} \left[ \| \boldsymbol{\epsilon} - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \|^2 \right] Lsimple(θ)=Et,x0,ϵ[∥ϵ−ϵθ(xt,t)∥2]
其中:
- t ∼ Uniform ( 1 , T ) t \sim \text{Uniform}(1, T) t∼Uniform(1,T)
- x 0 ∼ q ( x 0 ) \mathbf{x}_0 \sim q(\mathbf{x}_0) x0∼q(x0)
- ϵ ∼ N ( 0 , I ) \boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) ϵ∼N(0,I)
- x t = α ˉ t x 0 + 1 − α ˉ t ϵ \mathbf{x}_t = \sqrt{\bar{\alpha}_t} \mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t} \boldsymbol{\epsilon} xt=αˉtx0+1−αˉtϵ
关键结论
DDPM 通过训练一个网络 ϵ θ \boldsymbol{\epsilon}_\theta ϵθ 预测添加到样本中的噪声,最小化噪声预测的均方误差,从而实现数据生成。此目标等价于对数据分布的梯度(分数)进行匹配,与基于分数的生成模型有深刻联系。
补充内容(优化思路)
变分下界(VLB)最终简化公式的逐项解析与优化思路
最终VLB公式为:
VLB = E q ( x 1 ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] − ∑ t = 2 T E q ( x t ∣ x 0 ) [ D KL ( q ( x t − 1 ∣ x t , x 0 ) ∥ p θ ( x t − 1 ∣ x t ) ) ] − D KL ( q ( x T ∣ x 0 ) ∥ p ( x T ) ) \begin{align*} \text{VLB} = & \;\mathbb{E}_{q(\mathbf{x}_1 | \mathbf{x}_0)} \Big[ \log p_\theta(\mathbf{x}_0 | \mathbf{x}_1) \Big] \\ & - \sum_{t=2}^T \mathbb{E}_{q(\mathbf{x}_t | \mathbf{x}_0)} \left[ D_{\text{KL}} \Big( q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_{t-1} | \mathbf{x}_t) \Big) \right] \\ & - D_{\text{KL}} \Big( q(\mathbf{x}_T | \mathbf{x}_0) \parallel p(\mathbf{x}_T) \Big) \end{align*} VLB=Eq(x1∣x0)[logpθ(x0∣x1)]−t=2∑TEq(xt∣x0)[DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))]−DKL(q(xT∣x0)∥p(xT))
1. 重构项 (Reconstruction Term)
E q ( x 1 ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] \mathbb{E}_{q(\mathbf{x}_1 | \mathbf{x}_0)} \Big[ \log p_\theta(\mathbf{x}_0 | \mathbf{x}_1) \Big] Eq(x1∣x0)[logpθ(x0∣x1)]
-
含义:
衡量从第一步带噪样本 x 1 \mathbf{x}_1 x1 重建原始数据 x 0 \mathbf{x}_0 x0 的质量。- q ( x 1 ∣ x 0 ) q(\mathbf{x}_1 | \mathbf{x}_0) q(x1∣x0):前向过程第一步( x 0 → x 1 \mathbf{x}_0 \to \mathbf{x}_1 x0→x1)
- p θ ( x 0 ∣ x 1 ) p_\theta(\mathbf{x}_0 | \mathbf{x}_1) pθ(x0∣x1):反向生成过程的第一步( x 1 → x 0 \mathbf{x}_1 \to \mathbf{x}_0 x1→x0)
-
物理意义:
评估模型在轻度噪声水平( t = 1 t=1 t=1)下的数据重建能力。
对于图像数据,此项常建模为离散分布(如像素级交叉熵)或连续分布(如高斯似然)。 -
优化作用:
确保生成过程最终输出高质量样本。实际训练中此项影响较小(因 t = 1 t=1 t=1 噪声水平低)。
2. 去噪匹配项 (Denoising Matching Term)
− ∑ t = 2 T E q ( x t ∣ x 0 ) [ D KL ( q ( x t − 1 ∣ x t , x 0 ) ∥ p θ ( x t − 1 ∣ x t ) ) ] - \sum_{t=2}^T \mathbb{E}_{q(\mathbf{x}_t | \mathbf{x}_0)} \left[ D_{\text{KL}} \Big( q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_{t-1} | \mathbf{x}_t) \Big) \right] −t=2∑TEq(xt∣x0)[DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))]
-
含义:
核心优化项!要求反向生成过程 p θ p_\theta pθ 匹配前向过程的后验分布 q q q。- q ( x t − 1 ∣ x t , x 0 ) q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0) q(xt−1∣xt,x0):已知 x 0 \mathbf{x}_0 x0 和 x t \mathbf{x}_t xt 时 x t − 1 \mathbf{x}_{t-1} xt−1 的真实后验分布(可解析计算的高斯分布)
- p θ ( x t − 1 ∣ x t ) p_\theta(\mathbf{x}_{t-1} | \mathbf{x}_t) pθ(xt−1∣xt):参数化的反向生成模型(神经网络预测)
-
物理意义:
在每一步 t t t,强制生成模型从 x t \mathbf{x}_t xt 预测 x t − 1 \mathbf{x}_{t-1} xt−1 的分布接近理论最优去噪分布。 -
关键推导结论:
该KL散度可简化为 噪声预测的均方误差:
D KL ∝ ∥ ϵ − ϵ θ ( x t , t ) ∥ 2 D_{\text{KL}} \propto \| \boldsymbol{\epsilon} - \boldsymbol{\epsilon}_\theta (\mathbf{x}_t, t) \|^2 DKL∝∥ϵ−ϵθ(xt,t)∥2
其中 x t = α ˉ t x 0 + 1 − α ˉ t ϵ \mathbf{x}_t = \sqrt{\bar{\alpha}_t} \mathbf{x}_0 + \sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon} xt=αˉtx0+1−αˉtϵ, ϵ θ \boldsymbol{\epsilon}_\theta ϵθ 是预测噪声的神经网络。 -
优化作用:
主导整个训练过程(占损失函数权重的99%以上)。
将复杂的分布匹配问题转化为简单的监督学习:训练网络 ϵ θ \boldsymbol{\epsilon}_\theta ϵθ 预测加入的噪声 ϵ \boldsymbol{\epsilon} ϵ。
3. 先验匹配项 (Prior Matching Term)
− D KL ( q ( x T ∣ x 0 ) ∥ p ( x T ) ) - D_{\text{KL}} \Big( q(\mathbf{x}_T | \mathbf{x}_0) \parallel p(\mathbf{x}_T) \Big) −DKL(q(xT∣x0)∥p(xT))
-
含义:
衡量前向过程最终分布 q ( x T ∣ x 0 ) q(\mathbf{x}_T | \mathbf{x}_0) q(xT∣x0) 与预设先验 p ( x T ) p(\mathbf{x}_T) p(xT) 的相似度。- q ( x T ∣ x 0 ) = N ( x T ; α ˉ T x 0 , ( 1 − α ˉ T ) I ) q(\mathbf{x}_T | \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_T; \sqrt{\bar{\alpha}_T} \mathbf{x}_0, (1-\bar{\alpha}_T)\mathbf{I}) q(xT∣x0)=N(xT;αˉTx0,(1−αˉT)I)
- p ( x T ) = N ( 0 , I ) p(\mathbf{x}_T) = \mathcal{N}(\mathbf{0}, \mathbf{I}) p(xT)=N(0,I)(标准高斯分布)
-
物理意义:
确保前向过程结束时,噪声分布接近标准高斯分布(生成过程的起点)。 -
优化作用:
- 当 α ˉ T ≈ 0 \bar{\alpha}_T \approx 0 αˉT≈0 时(DDPM通常满足),此项趋近于0(因 q ( x T ∣ x 0 ) ≈ N ( 0 , I ) q(\mathbf{x}_T|\mathbf{x}_0) \approx \mathcal{N}(0, \mathbf{I}) q(xT∣x0)≈N(0,I))。
- 实际训练中常被忽略,因其不依赖可训练参数 θ \theta θ 且值极小。
整体优化思路分析
1. 核心优化目标
最大化 log p θ ( x 0 ) \log p_\theta(\mathbf{x}_0) logpθ(x0) 的下界(VLB),等价于最小化:
L VLB = − VLB = L 0 + ∑ t = 2 T L t + L T \mathcal{L}_{\text{VLB}} = -\text{VLB} = \mathcal{L}_0 + \sum_{t=2}^T \mathcal{L}_{t} + \mathcal{L}_T LVLB=−VLB=L0+t=2∑TLt+LT
其中:
- L 0 = − E [ log p θ ( x 0 ∣ x 1 ) ] \mathcal{L}_0 = -\mathbb{E}[\log p_\theta(\mathbf{x}_0|\mathbf{x}_1)] L0=−E[logpθ(x0∣x1)](重构损失)
- L t = E [ D KL ( q ∥ p θ ) ] \mathcal{L}_{t} = \mathbb{E}[D_{\text{KL}}(q \parallel p_\theta)] Lt=E[DKL(q∥pθ)](去噪匹配损失)
- L T = D KL ( q ( x T ∣ x 0 ) ∥ p ( x T ) ) \mathcal{L}_T = D_{\text{KL}}(q(\mathbf{x}_T|\mathbf{x}_0) \parallel p(\mathbf{x}_T)) LT=DKL(q(xT∣x0)∥p(xT))(先验匹配损失)
2. 实际训练简化
-
忽略 L T \mathcal{L}_T LT:
因 α ˉ T ≈ 0 \bar{\alpha}_T \approx 0 αˉT≈0,此项可忽略(接近0)。 -
简化 L 0 \mathcal{L}_0 L0:
用均方误差替代离散分布建模(如对于图像数据)。 -
主导项 L t \mathcal{L}_{t} Lt 的转化:
通过数学推导,将KL散度转化为噪声预测损失:
L t ∝ E x 0 , ϵ , t ∥ ϵ − ϵ θ ( x t , t ) ∥ 2 \mathcal{L}_{t} \propto \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}, t} \| \boldsymbol{\epsilon} - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \|^2 Lt∝Ex0,ϵ,t∥ϵ−ϵθ(xt,t)∥2 -
均匀时间步采样:
为稳定训练,对 t ∼ Uniform { 1 , . . . , T } t \sim \text{Uniform}\{1,...,T\} t∼Uniform{1,...,T} 采样并去权重:
L simple = E t , x 0 , ϵ ∥ ϵ − ϵ θ ( x t , t ) ∥ 2 \mathcal{L}_{\text{simple}} = \mathbb{E}_{t,\mathbf{x}_0,\boldsymbol{\epsilon}} \| \boldsymbol{\epsilon} - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \|^2 Lsimple=Et,x0,ϵ∥ϵ−ϵθ(xt,t)∥2
3. 物理意义图解
生成过程(反向): x_T ≈ N(0,I) → [pθ(x_{T-1}|x_T)] → ... → [pθ(x_0|x_1)] → x_0↑ 匹配 ↑ 匹配 ↑ 匹配
前向过程 : x_0 → [q(x1|x0)] → x_1 → ... → [q(x_T|x_{T-1})] → x_T重构项↑ 去噪匹配项↑ 先验匹配项↑
4. 为什么此优化有效?
- 解耦复杂性:
将高维数据分布匹配问题分解为 T T T 个简单的高斯分布匹配任务。 - 渐进式优化:
通过时间步 t t t 控制噪声水平,从易(高噪声)到难(低噪声)逐步训练。 - 闭式解指导:
利用前向过程后验 q ( x t − 1 ∣ x t , x 0 ) q(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0) q(xt−1∣xt,x0) 的解析解提供训练目标。 - 隐式分数匹配:
噪声预测等价于学习数据分布的梯度场( ϵ θ ∝ − ∇ x t log p ( x t ) \boldsymbol{\epsilon}_\theta \propto -\nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t) ϵθ∝−∇xtlogp(xt))。
总结
| 项 | 含义 | 优化作用 | 实际处理 |
|---|---|---|---|
| 重构项 | 从 x 1 \mathbf{x}_1 x1 重建 x 0 \mathbf{x}_0 x0 | 保证最终输出质量 | 保留或用MSE替代 |
| 去噪匹配项 | 匹配反向生成与前向后验分布 | 核心训练目标(>99%权重) | 转化为噪声预测损失 |
| 先验匹配项 | 对齐 x T \mathbf{x}_T xT 与标准高斯 | 确保生成起点正确 | 忽略(值≈0) |
DDPM的创新优化思路:
将生成建模问题转化为序列化的噪声预测任务,通过:
- 利用前向过程后验的闭式解提供训练目标
- 将KL散度转化为均方误差损失
- 均匀采样时间步简化训练
使扩散模型可稳定训练于高维数据(如图像、音频),成为生成式AI的核心框架。
相关文章:

DDPM优化目标公式推导
DDPM优化目标公式推导 DDPM优化目标公式推导**1. 问题定义****2. 优化目标:最大化对数似然****3. 变分下界的分解****4. 关键步骤:简化 KL 散度项****(a) 后验分布 q ( x t − 1 ∣ x t , x 0 ) q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0) q(xt…...
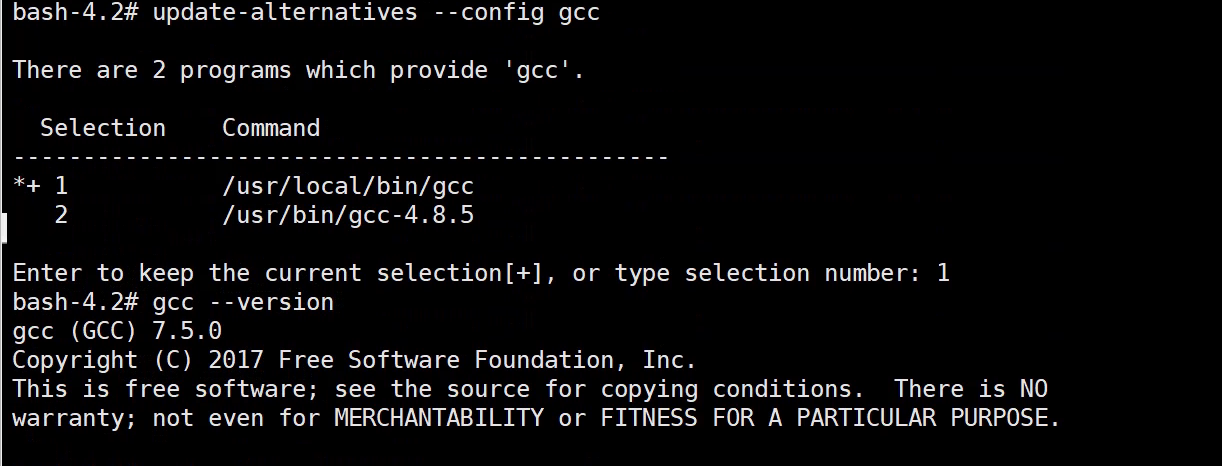
CentOS 7如何编译安装升级gcc至7.5版本?
CentOS 7如何编译安装升级gcc版本? 由于配置CentOS-SCLo-scl.repo与CentOS-SCLo-scl-rh.repo后执行yum install -y devtoolset-7安装总是异常,遂决定编译安装gcc7.5 # 备份之前的yum .repo文件至 /tmp/repo_bak 目录 mkdir -p /tmp/repo_bak && cd /etc…...

为什么React列表项需要key?(React key)(稳定的唯一标识key有助于React虚拟DOM优化重绘大型列表)
文章目录 1. **帮助 React 识别列表项的变化**2. **性能优化**3. **避免组件状态混乱**4. **为什么使用 rpid 作为 key**5. **不好的做法示例**6. **✅ 正确的做法** 在 React 中添加 key{item.rpid} 是非常重要的,主要有以下几个原因: 1. 帮助 React 识…...
)
Playwright自动化测试全栈指南:从基础到企业级实践(2025终极版)
引言 在Web应用复杂度指数级增长的今天,传统自动化测试工具面临动态渲染适配难、多浏览器兼容差、测试稳定性低三大挑战。微软开源的Playwright凭借跨浏览器支持、自动等待机制和原生异步架构,成为新一代自动化测试的事实标…...

飞牛云一键设置动态域名+ipv6内网直通访问内网的ssh服务-家庭云计算专家
IPv6访问SSH的难点与优势并存。难点主要体现在网络环境支持不足:部分ISP未完全适配IPv6协议,导致客户端无法直接连通;老旧设备或工具(如Docker、GitHub)需额外配置才能兼容IPv6,技术门槛较高;若…...

虚实共生时代的情感重构:AI 恋爱陪伴的崛起、困局与明日图景
一、虚拟恋人:从技术幻想到情感刚需的跨越 在 5G 网络编织的数字浪潮里,AI 驱动的虚拟恋人正打破次元界限。深度学习算法剖析 3000 万段真实对话语料库,搭配 VR 设备带来的多维度交互体验,如今的虚拟对象已能精准模拟瞳孔微表情&…...
!!!C++语言(嵌入式八股文,嵌入式面经))
嵌入式面试高频(5)!!!C++语言(嵌入式八股文,嵌入式面经)
一、C有几种传值方式之间的区别 一、值传递(Pass by Value) 机制:创建参数的副本,函数内操作不影响原始数据语法:void func(int x)特点: 数据安全:原始数据不受影响性能开销:需要复…...

C++动态规划-线性DP
这是一套C线性DP题目的答案。如果需要题目,请私信我,我将会更新题干 P1:单子序列最大和 #include <bits/stdc.h> using namespace std; int n,A,B,C; int a[200005]; int s[200005]; int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)…...

Java高级 | 【实验七】Springboot 过滤器和拦截器
隶属文章:Java高级 | (二十二)Java常用类库-CSDN博客 系列文章:Java高级 | 【实验一】Springboot安装及测试 |最新-CSDN博客 Java高级 | 【实验二】Springboot 控制器类相关注解知识-CSDN博客 Java高级 | 【实验三】Springboot 静…...

es地理信息索引的类型以及geo_point和geo_hash的关系
Elasticsearch中地理信息索引的主要数据类型有两种: geo_point:用于存储单个地理点坐标(如纬度/经度),支持精确位置查询和基于距离的搜索操作。geo_shape:用于存储复杂的地理形状(如点、线、多…...

深入理解 Spring IOC:从概念到实践
目录 一、引言 二、什么是 IOC? 2.1 控制反转的本质 2.2 类比理解 三、Spring IOC 的核心组件 3.1 IOC 容器的分类 3.2 Bean 的生命周期 四、依赖注入(DI)的三种方式 4.1 构造器注入 4.2 Setter 方法注入 4.3 注解注入(…...

Vue解决开发环境 Ajax 跨域问题
一、前言 在使用 Vue 进行前后端分离开发时,前端通常运行在本地开发服务器(如 http://localhost:8080),而后端接口可能部署在其他域名或端口下(如 http://api.example.com:3000)。这时就可能出现 跨域&…...

行为设计模式之Command (命令)
行为设计模式之Command (命令) 前言: 需要发出请求的对象(调用者)和接收并执行请求的对象(执行者)之间没有直接依赖关系时。比如遥控器 每个按钮绑定一个command对象,这个Command对…...
)
若依添加添加监听容器配置(删除键,键过期)
1、配置Redis的键触发事件 # 基础配置 bind 0.0.0.0 # 允许所有IP连接 protected-mode no # 关闭保护模式(生产环境建议结合密码使用) port 6379 # 默认端口 daemonize no …...

NeRF 技术深度解析:原理、局限与前沿应用探索(AI+3D 产品经理笔记 S2E04)
引言:光影的魔法师——神经辐射场概览 在前三篇笔记中,我们逐步揭开了 AI 生成 3D 技术的面纱:从宏观的驱动力与价值(S2E01),到主流技术流派的辨析(S2E02),再到实用工具的…...

ROS2,工作空间中新建了一个python脚本,需要之后作为节点运行。告诉我步骤?
提问 ROS2,工作空间中新建了一个python脚本,需要之后运行。告诉我步骤? 大概要包括而不限于:chmod给可执行权限、setup.py中entry point的配置,如果在launch文件中要使用,还涉及到launch.py文件的配置。最…...

【AI智能体】Spring AI MCP 从使用到操作实战详解
目录 一、前言 二、MCP 介绍 2.1 什么是MCP 2.2 MCP 核心特点 2.3 MCP 核心价值 2.4 MCP 与Function Calling 区别 三、Spring AI MCP 架构介绍 3.1 整体架构 3.1.1 三层架构实现说明 3.2 服务端与客户端 3.2.1 MCP 服务端 3.2.1 MCP 客户端 3.3 MCP中SSE和STDIO区…...

Vue:Ajax
AJAX 允许我们在不刷新页面的情况下与服务器交互,实现:动态加载数据,提交表单信息,实时更新内容,与后端 API 通信。通常使用专门的 HTTP 客户端库来处理 AJAX 请求。 npm install axiosimport axios from axios;expor…...

法律大语言模型(Legal LLM)技术架构
目录 摘要 1 法律AI大模型技术架构 1.1 核心架构分层 1.2 法律知识增强机制 2 关键技术突破与对比 2.1 法律专用组件创新 2.2 性能对比(合同审查场景) 3 开发部署实战指南 3.1 环境搭建流程 3.2 合同审查代码示例 4 行业应用与挑战 4.1 典型场景效能提升 4.2 关…...

理解 RAG_HYBRID_BM25_WEIGHT:打造更智能的混合检索增强生成系统
目录 理解 RAG_HYBRID_BM25_WEIGHT:打造更智能的混合检索增强生成系统 一、什么是 Hybrid RAG? 二、什么是 RAG_HYBRID_BM25_WEIGHT? 三、参数设置示例 四、什么时候该调整它? 五、实战建议 六、总结 理解 RAG_HYBRID_BM25…...

Hive终极性能优化指南:从原理到实战
摘要:本文系统总结Hive在生产环境的核心调优手段,涵盖执行引擎选择、存储优化、SQL技巧、资源调配及数据倾斜解决方案,附可复用的参数配置与实战案例。 一、执行引擎优化:突破MapReduce瓶颈 启用Tez/Spark引擎 优势&am…...

第六十二节:深度学习-加载 TensorFlow/PyTorch/Caffe 模型
在计算机视觉领域,OpenCV的DNN(深度神经网络)模块正逐渐成为轻量级模型部署的利器。本文将深入探讨如何利用OpenCV加载和运行三大主流框架(TensorFlow、PyTorch、Caffe)训练的模型,并提供完整的代码实现和优化技巧。 一、OpenCV DNN模块的核心优势 OpenCV的DNN模块自3.3…...
MobaXterm配置跳转登录堡垒机
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 背景操作步骤 背景 主要是为了能通过MobaXterm登录堡垒机,其中需要另外一台服务器进行跳转登录 操作步骤 MobaXterm登录堡垒机的操作,需…...

零基础在实践中学习网络安全-皮卡丘靶场(第八期-Unsafe Filedownload模块)
这期内容更是简单和方便,毕竟谁还没在浏览器上下载过东西,不过对于url的构造方面,可能有一点问题,大家要多练手 介绍 不安全的文件下载概述 文件下载功能在很多web系统上都会出现,一般我们当点击下载链接,…...

测试 FreeSWITCH 的 mod_loopback
bgapi originate loopback/answer,park/default/inline park inline show channels as xml show calls as xml 有 2 个 channels 有 2 个 calls 比较有意思 在 loopback-a 是播放 wav 在 loopback-b 上可以录音 这就是回环 有什么用呢? 除了做测试&#x…...

【C++快读快写】
算法竞赛中用于解决卡常问题 int rd(){int k 0;char c getchar();while(!isdigit(c)){c getchar();}while(isdigit(c)){k (k << 1) (k << 3) (c^0), c getchar();}return k; }void wr(int x) {if (x > 9)wr(x / 10);putchar((x % 10) ^ 0); }用法&#x…...
)
测试(面经 八股)
目录 前言 一,软件测试(定义) 1,定义 2,目的 3,价值 4,实践 二,软件测试(目的) 1,找 bug 2,验证达标 3,质量评价…...
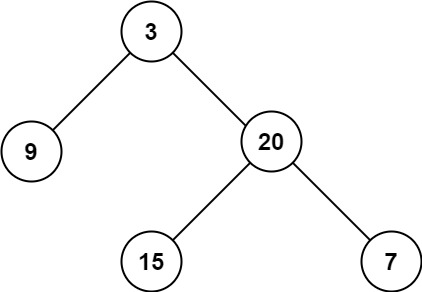
[面试精选] 0104. 二叉树的最大深度
文章目录 1. 题目链接2. 题目描述3. 题目示例4. 解题思路5. 题解代码6. 复杂度分析 1. 题目链接 104. 二叉树的最大深度 - 力扣(LeetCode) 2. 题目描述 给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点…...

图上合成:用于大型语言模型持续预训练的知识合成数据生成
摘要 大型语言模型(LLM)已经取得了显著的成功,但仍然是数据效率低下,特别是当学习小型,专业语料库与有限的专有数据。现有的用于连续预训练的合成数据生成方法集中于文档内内容,而忽略了跨文档的知识关联&a…...
 ---MySQL 8.4 新特性与变量变更)
MYSQL(二) ---MySQL 8.4 新特性与变量变更
MySQL 8.4 新特性与变量变更 作者:程序员LSP 分类:MySQL 8.4 教程 / 新特性 / 升级指南 更新时间:2025年6月 📌 前言 MySQL 8.4 是当前最新的稳定版本,相较于 8.0 系列,在审计日志、高可用、性能调优、认证…...
