【统计方法】树模型,ensemble,bagging, boosting
决策树基础
回归树
理论上,决策区域可以有任何形状。•
然而,我们选择将预测空间划分为高维矩形或框,这是为了简单和易于解释结果预测模型
- 目标:将预测空间划分为矩形区域,最小化残差平方和(RSS)
∑ j = 1 J ∑ i ∈ R j ( y i − y ^ R j ) 2 \sum_{j=1}^J \sum_{i \in R_j} (y_i - \hat{y}_{R_j})^2 ∑j=1J∑i∈Rj(yi−y^Rj)2- y ^ R j \hat{y}_{R_j} y^Rj 为区域 R j R_j Rj 内样本响应的均值
- 示例(棒球运动员薪资预测):
- 关键分裂规则:
- R 1 = { X ∣ Years < 4.5 } R_1 = \{X \mid \text{Years} < 4.5\} R1={X∣Years<4.5}
- R 2 = { X ∣ Years ≥ 4.5 , Hits < 117.5 } R_2 = \{X \mid \text{Years} \geq 4.5, \text{Hits} < 117.5\} R2={X∣Years≥4.5,Hits<117.5}
- R 3 = { X ∣ Years ≥ 4.5 , Hits ≥ 117.5 } R_3 = \{X \mid \text{Years} \geq 4.5, \text{Hits} \geq 117.5\} R3={X∣Years≥4.5,Hits≥117.5}
- 区域𝑅1、𝑅2和𝑅3称为终端节点。
- 决策树通常是上下颠倒的,因为叶子在树的底部。
- 沿着预测空间被分割的树的点被称为内部节点。
- 结论:经验年限(Years)是薪资决定性因素,高经验球员中安打数(Hits)显著影响薪资
- 分类之后节点里的数据做平均作为预测值,分类任务则取众数
- 关键分裂规则:
分类树
-
预测方式:将样本划分至终端节点,预测该节点内最频繁的类别
最上面的节点是最重要的,对比线性模型,我们看P值,< 0.05说明重要
-
分裂标准:
-
基尼指数(衡量节点纯度):
Gini指数是衡量分类节点纯度的重要指标。
-
Gini指数衡量了所有 K K K个类别的总方差。
- 当所有 p ^ m k \hat{p}_{mk} p^mk(第 m m m个节点第 k k k类的比例)值都接近0或1时,Gini指数取较小值。
- 这种情况意味着节点中某个类别占多数,节点较纯。
-
因此,Gini指数被用来衡量节点的纯度(purity)。
- 较小的Gini值表明该节点中的观测值主要来自同一个类别。
总结来说,Gini指数越低,节点纯度越高,分类效果越好。
G = ∑ k = 1 K p ^ m k ( 1 − p ^ m k ) G = \sum_{k=1}^{K} \hat{p}_{mk}(1 - \hat{p}_{mk}) G=∑k=1Kp^mk(1−p^mk)
- p ^ m k \hat{p}_{mk} p^mk:区域 m m m 中第 k k k 类样本比例
- 值越小表示节点纯度越高
-
-
熵(替代指标):
D = − ∑ j = 1 J ∑ k = 1 K p j k log p j k D = -\sum_{j=1}^{J} \sum_{k=1}^{K} p_{jk} \log p_{jk} D=−∑j=1J∑k=1Kpjklogpjk
熵(Entropy)和基尼指数(Gini Index)都是衡量分类树中节点纯度的指标,但它们有以下区别:
-
定义不同
-
基尼指数:
G = ∑ k = 1 K p k ( 1 − p k ) = 1 − ∑ k = 1 K p k 2 G = \sum_{k=1}^K p_{k}(1 - p_{k}) = 1 - \sum_{k=1}^K p_k^2 G=k=1∑Kpk(1−pk)=1−k=1∑Kpk2
衡量节点中类别的不纯度,值越小越纯。 -
熵:
D = − ∑ k = 1 K p k log p k D = -\sum_{k=1}^K p_k \log p_k D=−k=1∑Kpklogpk
衡量信息的不确定性,值越小越纯。
-
-
数值范围和敏感性
- 基尼指数最大值通常是0.5(对于二分类,类别均匀分布时),对极端概率值敏感度较低。
- 熵最大值为 log K \log K logK,对概率分布更敏感,尤其是概率接近0或1时变化更剧烈。
-
计算复杂度
- 基尼指数计算相对简单,速度更快。
- 熵涉及对数运算,计算略复杂。
-
算法应用
- CART决策树常用基尼指数作为分裂标准。
- ID3和C4.5决策树常用熵和信息增益。
-
表现差异
在实际应用中,基尼指数和熵通常效果相近,差异不大,选择更多基于算法设计和偏好。
总结:
基尼指数和熵都是衡量节点纯度的指标,基尼指数偏重简单和计算效率,熵则有更强的信息理论基础和敏感度。 -

树的构建与剪枝
我们希望将特征空间划分为𝐽不同的区域。
但是尝试每一个可能的分区在计算上是不可行的。
相反,我们使用自上而下的贪婪方法(递归二进制分割):在每一步上,选择最佳的分割。在产生的子空间上递归地重复这个过程。
-
递归二叉分裂:
-
流程:从根节点(全体数据)开始,贪心地选择能最大程度降低RSS(回归)或提升纯度(分类)的分裂点
-
缺陷:局部最优且易过拟合
通过递归二叉分割生长的树可以产生深度、复杂的树,可以完美地拟合训练数据。这样的树可能会过拟合,因为它捕获的是噪声而不是信号
这导致高方差和较差的泛化
-
-
剪枝(控制复杂度):
- 代价复杂度剪枝 Cost-Complexity Pruning (the weakest link pruning):
$ C_{\alpha}(T) = \text{RSS} + \alpha |T| $- α \alpha α:权衡模型复杂度与拟合度的调参参数
- ∣ T ∣ |T| ∣T∣:子树节点数
- 代价复杂度剪枝 Cost-Complexity Pruning (the weakest link pruning):
使用决策树进行预测
我们将预测空间划分为:
𝑋1,𝑋2,…,𝑋𝑝的可能值的集合,分为𝐽不同的和不重叠的区域,𝑅1,𝑅2,…,𝑅𝐽。
对于每个落在𝑅𝑗区域的观测值,我们做相同的预测,这只是𝑅𝑗中训练观测值的响应值的平均值。
线性模型与树模型的对比

-
图1(Graph 1)展示了当特征与响应变量之间的关系可被线性模型很好拟合时,线性模型的表现优于树模型。
-
图2(Graph 2)展示了树模型拟合的结果,虽然逼近了线性边界,但由于分段结构,表现稍差于线性模型。
-
图3(Graph 3)和图4(Graph 4)展示了特征与响应之间的复杂非线性关系:
- 线性模型(图3)无法很好捕捉这种非线性边界。
- 树模型(图4)通过分区分割能更灵活地拟合复杂形状,表现更合适。
总结:
- 如果数据关系接近线性,线性模型更优。
- 如果数据关系复杂且非线性,树模型更适合。
树模型的优缺点
优点(Advantages)
- 树模型非常容易向人解释。
- 有人认为决策树与人类的决策过程较为接近。
- 树模型可以图形化展示,直观易懂。
- 能处理不同类型的数据,不需要进行数据缩放。
缺点(Disadvantages)
- 树模型的预测准确度通常不及其他一些回归和分类方法。
- prone to over-fitting
树模型集成方法详解
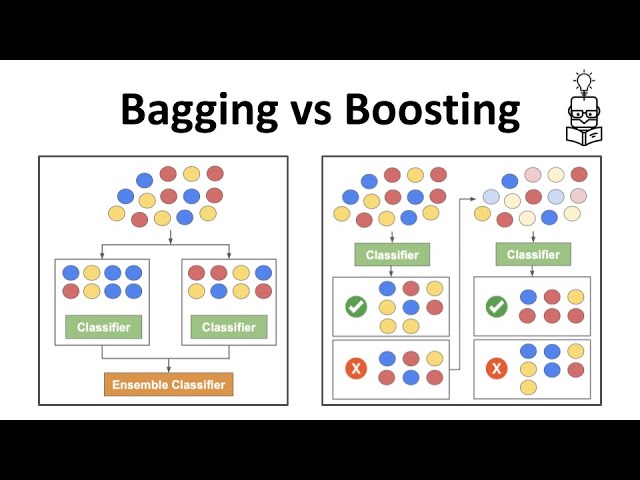
树模型集成(Ensemble of Trees)
- 构建多个决策树
- 结合多个树的结果,形成更稳定、更准确的预测器
关键思想
- 对树进行采样(如自助采样 bootstrap)
- 每次分裂时使用随机子集特征
- 聚合预测结果:
- 分类任务采用多数投票
- 回归任务采用平均值
常用方法
- Bagging:并行构建多棵树并平均结果
- 随机森林(Random Forest):Bagging 加上随机特征选择
- Boosting:序列式构建树以改进误差
集成方法的优势在于通过聚合降低方差,提高模型鲁棒性。
Bagging(Bootstrap Aggregating)
- Bagging是一种降低模型方差的通用方法,特别适用于决策树。
- 原理是对训练数据集进行多次自助采样,生成多个训练子集。
- 对每个子集训练独立的树模型,最终对预测结果求平均。
Bagging的方差原理
- 给定 n n n个独立样本,均值的方差是 σ 2 / n \sigma^2 / n σ2/n。
- 通过平均多个样本,减少方差。
- 由于只有一个训练集,使用bootstrap采样制造多个训练集。
Bagging流程
-
从原始训练集采样 B B B个bootstrap样本。
-
训练 B B B个树模型,记第 b b b个树的预测为 f ^ b ∗ ( x ) \hat{f}_b^*(x) f^b∗(x)。
-
集成预测为:
f ^ ( x ) = 1 B ∑ b = 1 B f ^ b ∗ ( x ) \hat{f}(x) = \frac{1}{B} \sum_{b=1}^B \hat{f}_b^*(x) f^(x)=B1b=1∑Bf^b∗(x)
OOB误差估计(Out-of-Bag Error)
-
由于每棵树仅使用约 2 / 3 2/3 2/3的样本进行训练,剩余 1 / 3 1/3 1/3样本称为OOB样本。
OOB(Out-Of-Bag)样本是在bagging过程中划分的,具体来说:
- 在bagging时,每棵树的训练数据是通过bootstrap采样从原始训练集中随机有放回抽取的一个子样本。
- 由于是有放回抽样,平均而言,大约2/3的样本会被抽到用于训练该树。
- 剩下的约1/3样本没有被抽中,这部分样本就是对应这棵树的OOB样本。
换句话说,OOB样本是bagging抽样后自动形成的,它不是提前划分的固定测试集,而是每棵树“未见过”的样本。
利用这些OOB样本,可以在训练阶段对模型性能进行无偏估计,相当于一种交叉验证。
总结:
OOB样本是在bagging采样时自然划分出来的,属于bagging过程的一部分,而不是在bagging前固定划分的。 -
利用OOB样本对对应未训练该样本的树进行预测,取平均值作为该样本的预测。
-
OOB误差相当于一种留一交叉验证(LOO CV)误差估计,且计算方便。
随机森林(Random Forest)
- 随机森林在Bagging基础上,增加分裂时随机选取 m m m个特征作为候选变量。
- 每次分裂只从这 m m m个特征中选最佳分裂变量,降低树间相关性,进一步减少方差。
- 通常 m ≈ p m \approx \sqrt{p} m≈p,其中 p p p为总特征数。
随机森林伪代码
设置模型数B
for i = 1 to B:
生成bootstrap样本
训练决策树:
每次分裂:
从p个特征中随机选m个
选择最佳分裂特征
endfor
Boosting方法
- Boosting是另一种集成思想,树模型按序列顺序依次训练。
- 每棵树使用之前树的错误信息,重点拟合残差。
- 通过逐步修正误差,提高整体预测性能。
Boosting基本思想
- 与Bagging不同,Boosting模型是依赖的序列结构。
- 最终模型为多个弱学习器的加权和。
- 通过学习率 λ \lambda λ控制每一步改进的幅度,防止过拟合。
Boosting流程(回归树示例)
-
初始化预测模型 f ^ ( 0 ) ( x ) = 0 \hat{f}^{(0)}(x) = 0 f^(0)(x)=0,残差 r i = y i r_i = y_i ri=yi。
-
对 b = 1 , . . . , B b=1,...,B b=1,...,B:
-
拟合树模型 f ^ b \hat{f}_b f^b到残差 r r r。
-
更新模型:
f ^ ( b ) ( x ) = f ^ ( b − 1 ) ( x ) + λ f ^ b ( x ) \hat{f}^{(b)}(x) = \hat{f}^{(b-1)}(x) + \lambda \hat{f}_b(x) f^(b)(x)=f^(b−1)(x)+λf^b(x) -
更新残差:
r i ← r i − λ f ^ b ( x i ) r_i \leftarrow r_i - \lambda \hat{f}_b(x_i) ri←ri−λf^b(xi)
-
-
最终模型为所有加权树的和。
需要调节的参数
- 树的个数 B B B
- 学习率 λ \lambda λ(通常为0.001到0.01)
- 树的深度 d d d(如 d = 1 d=1 d=1即树桩)
其他Boosting变体
- AdaBoost:针对分类,重加权错误样本,组合弱分类器。
- 随机梯度提升(Stochastic Gradient Boosting):每次迭代使用训练集子样本,增强泛化能力。
- XGBoost:高效的梯度提升实现,支持正则化,处理缺失值,广泛应用。
Bagging与Boosting对比
| 特性 | Bagging | Boosting |
|---|---|---|
| 学习器训练方式 | 独立、并行 independently | 序列式依赖 sequentially |
| 树的复杂度 | 复杂树 | 通常为弱学习器(树桩) |
| 参数调节 | 参数较少 | 参数较多,需细调 |
| 目标 | 降低方差 | 降低偏差和方差 |
总结
- 决策树简单易解释,但单棵树性能有限。
- Bagging通过并行构建多棵树降低方差。
- 随机森林在Bagging基础上增加特征随机化,进一步提升性能。
- Boosting通过序列训练和残差拟合,提升预测准确度。
- 随机森林和Boosting是监督学习中效果领先的方法,但解释性较弱。
- 可通过变量重要性(如基尼指数减少)评估特征影响。
相关文章:

【统计方法】树模型,ensemble,bagging, boosting
决策树基础 回归树 理论上,决策区域可以有任何形状。• 然而,我们选择将预测空间划分为高维矩形或框,这是为了简单和易于解释结果预测模型 目标:将预测空间划分为矩形区域,最小化残差平方和(RSS&#x…...

【选配电脑】CPU核显工作机控制预算5000
【选配电脑】CPU核显工作机控制预算5000 1.背景2.配置及估价3.选配的说明 1.背景 不需要独立显卡,内存,硬盘尽量大; 预算控制到5000, 主板型号,电源功率支持后续添加独立显卡。 时间节点:2025.06.07 2.配…...
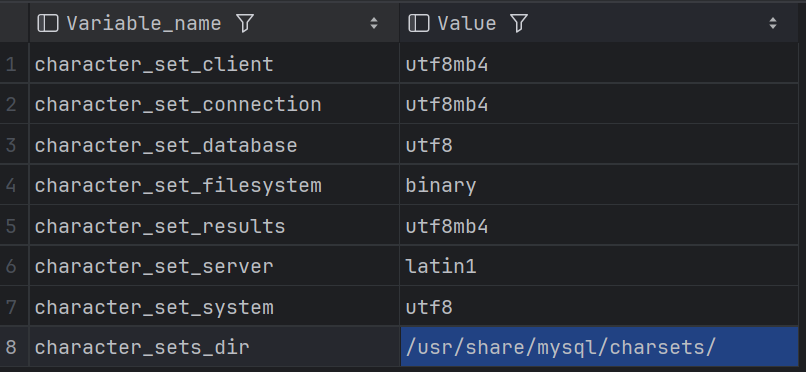
Mysql 插入中文乱码
session范围 查看数据库编码: show variables like %char%; # MySQL 5.7 字符集强制配置 # 修复 character_set_databaselatin1 等问题 [mysqld] character-set-server utf8mb4 collation-server utf8mb4_unicode_ci init_connect SET NAMES utf8mb4[client] d…...

UserAgent包名识别工具
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 背景具体实现 背景 为了更准确地分析用户下单行为的来源渠道,并实现精细化运营与风险控制,我们希望在用户下单时,能够通过请求中…...

96.如何使用C#实现串口发送? C#例子
Nuget包名称 System.IO.Ports 参考代码 using System; using System.IO.Ports; using System.Threading;namespace test {class Program{static void Main(){SerialPort port new SerialPort("COM1", 9600); // 配置串口port.Open();Timer timer new Timer((_) &…...

【工具使用】STM32CubeMX-FreeRTOS操作系统-信号标志、互斥锁、信号量篇
一、概述 无论是新手还是大佬,基于STM32单片机的开发,使用STM32CubeMX都是可以极大提升开发效率的,并且其界面化的开发,也大大降低了新手对STM32单片机的开发门槛。 本文主要讲述STM32芯片FreeRTOS信号标志、互斥锁和信号…...

[P2P]并发模式
设备可以同时作为 P2P Client 监听其他P2P请求,需要硬件和驱动支持。 //某些高级Wi-Fi芯片(如高通、博通)支持 Concurrent Mode(并发模式 GO 如果GO已经有一个client,大多数支持接受新的P2P Discovery。默认情况下会…...

Cloudflare 免费域名邮箱 支持 Catch-all 无限别名收件
本文首发于只抄博客,欢迎点击原文链接了解更多内容。 前言 与自建 Poste.io 还有 Serv00 邮局不同,Cloudflare 的域名邮箱并不需要 VPS,也没有复杂的配置。只要有一个托管在 Cloudflare 的域名就可以部署,像是常见的免费域名 eu.org 或者 dpdns.org 都是可以使用的。 需要…...
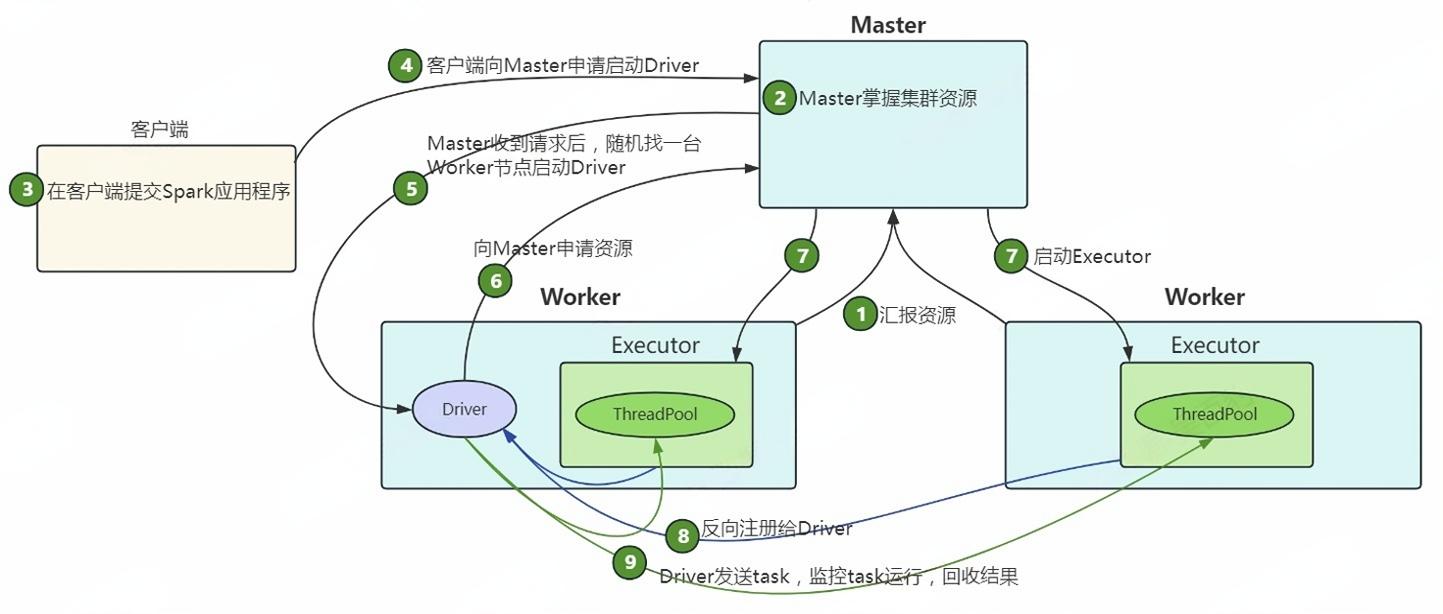
大数据Spark(六十一):Spark基于Standalone提交任务流程
文章目录 Spark基于Standalone提交任务流程 一、Standalone-Client模式 1、提交命令 2、任务执行流程 二、Standalone-Cluster模式 1、提交命令 2、任务执行流程 Spark基于Standalone提交任务流程 在Standalone模式下,Spark的任务提交根据Driver程序运行的位…...

学习记录:DAY32
Electron 开发之旅:从入门到实践 前言 接续上一篇 blog,这篇的内容主要和 Electron 有关。 课设不是特别想做下去了,实际核心代码大概只有 3,4 百行左右,比较水…… 或许会把 Docker 的部署也做一做(权当是…...

next,react封装axios,http请求
import axios from axios;//声明一个基础接口变量1 let base_url; //配置开发环境 if (process.env.NODE_ENV development) {base_url "http://127.0.0.1/"; } // 配置生产环境 if (process.env.NODE_ENV production) {base_url "http://127.0.0.1/"; …...

元图CAD:一键解锁PDF转CAD,OCR技术赋能高效转换
在建筑、工程与制造领域,图纸的精准性与高效协作是项目成功的关键。然而,传统PDF文件中的文字和图形往往难以直接编辑,手动输入不仅耗时易错,还可能因格式问题导致信息丢失。元图CAD凭借创新的OCR文字识别技术,重新定义…...

Android 平台RTSP/RTMP播放器SDK接入说明
一、技术背景 自2015年起,大牛直播SDK持续深耕音视频直播领域,自主研发并迭代推出跨平台 RTSP/RTMP 播放模块,具备如下核心优势: 全平台兼容:支持 Android/iOS/Windows/Linux 等主流系统; 超低延迟&#…...

Nodejs工程化实践:构建高性能前后端交互系统
一、工程架构设计 1.1 现代化项目初始化 采用多包管理架构: mkdir content-platform && cd content-platform npm init -y npx lerna init mkdir -p {packages/client,packages/server,packages/shared} 关键模块划分: client/: 基于Next.js…...

STM32什么是寄存器
提示:文章 文章目录 前言一、背景二、2.12.2 三、3.1 总结 前言 前期疑问: 1、什么是寄存器? 答:在4GB的地址空间中,512MB的block2上,每4个字节组成32位,这个32位为一个单元,控制&a…...

Linux 的 find 命令使用指南
精通 Linux 的 find 命令:终极使用指南 在 Linux 系统中,find 命令是文件搜索的瑞士军刀,它能基于多种条件在目录树中精准定位文件。无论你是系统管理员还是开发者,掌握 find 都能极大提升工作效率。本文将深入解析 find 的核心用法,并附赠实用示例! 一、基础语法结构 …...

第六个微信小程序:教师工具集
源于工作需要,下面开始。 安装及使用 | Taro 文档 vscode 代码管理 git 辅助 开发技术如上: 1.开始创建模板 taro4.1.1 $ taro init teachers-tools 2.用vsocde开始吧。 选择 第二个文件夹找一。 (base) PS D:\react\teachers-tools> pnpm…...

记录一个用了很久的git提交到github和gitee比较方便的方法
在当前git init后,在隐藏的git文件夹中找到config文件 [user]name thels [remote "github"]url your github repository urlfetch refs/heads/*:refs/remotes/origin/* [remote "gitee"]url your gitee repository urlfetch refs/heads/*:…...

Qt Qml模块功能及功能解析
QtQml 是 Qt 6.0 中用于声明式 UI 开发和应用程序逻辑的核心模块,它提供了 QML 语言的支持和运行时环境。 一、主要功能 1. QML 语言支持 QML 语法解析:支持 QML (Qt Meta-Object Language 或 Qt Modeling Language) 的完整语法 JavaScript 集成&…...

前端八股之JS的原型链
1.原型的定义 每一个对象从被创建开始就和另一个对象关联,从另一个对象上继承其属性,这个另一个对象就是 原型。 当访问一个对象的属性时,先在对象的本身找,找不到就去对象的原型上找,如果还是找不到,就去…...

NLP学习路线图(二十九):BERT及其变体
在自然语言处理(NLP)领域,一场静默的革命始于2017年。当谷歌研究者发表《Attention is All You Need》时,很少有人预料到其中提出的Transformer架构会彻底颠覆NLP的发展轨迹,更催生了以GPT系列为代表的语言模型风暴,重新定义了人类与机器的交互方式。 一、传统NLP的瓶颈:…...

机器翻译模型笔记
机器翻译学习笔记(简体中文) 1. 任务概述 目标:将英文句子翻译成简体中文。 示例: 输入:Tom is a student. 输出:汤姆是一个学生。 框架:Seq2Seq(序列到序列)模型。…...

Ref vs. Reactive:Vue 3 响应式变量的最佳选择指南
Ref vs. Reactive:Vue 3 响应式变量的最佳选择指南 在 Vue 3 的 Composition API 中,ref 和 reactive 是创建响应式数据的两种主要方式。许多开发者经常困惑于何时使用哪种方式。本文将深入对比两者的差异,帮助您做出最佳选择。 核心概念解…...
像大语言模型(LLMs)一样“会思考”)
让视觉基础模型(VFMs)像大语言模型(LLMs)一样“会思考”
视觉检测器的演进:从 DETR 到 Grounding-DINO DINO-R1 的基础是 Grounding-DINO,而 Grounding-DINO 本身是一系列视觉检测器演进的结果。理解这个发展过程对掌握 DINO-R1 的核心技术至关重要。 DETR:用 Transformer 革新目标检测 在 DETR&…...

现代前端框架的发展与演进
现代前端框架的发展与演进是一个非常值得关注的话题,反映了整个前端生态系统的不断演化与技术深度的提升。以下是这一趋势的详细解析: 📈 现代前端框架的发展与演进 🔹 第一阶段:jQuery 时代(2006-2013&am…...

【LLM-Agent】智能体的记忆缓存设计
note 实践:https://modelscope-agent.readthedocs.io/zh-cn/latest/modules/memory.html 文章目录 note一、Agent的记忆实现二、相关综述三、记忆体的构建四、cursor的记忆设计1. 记忆生成提示词2. 记忆评估提示词 五、记忆相关的MCPReference 一、Agent的记忆实现…...
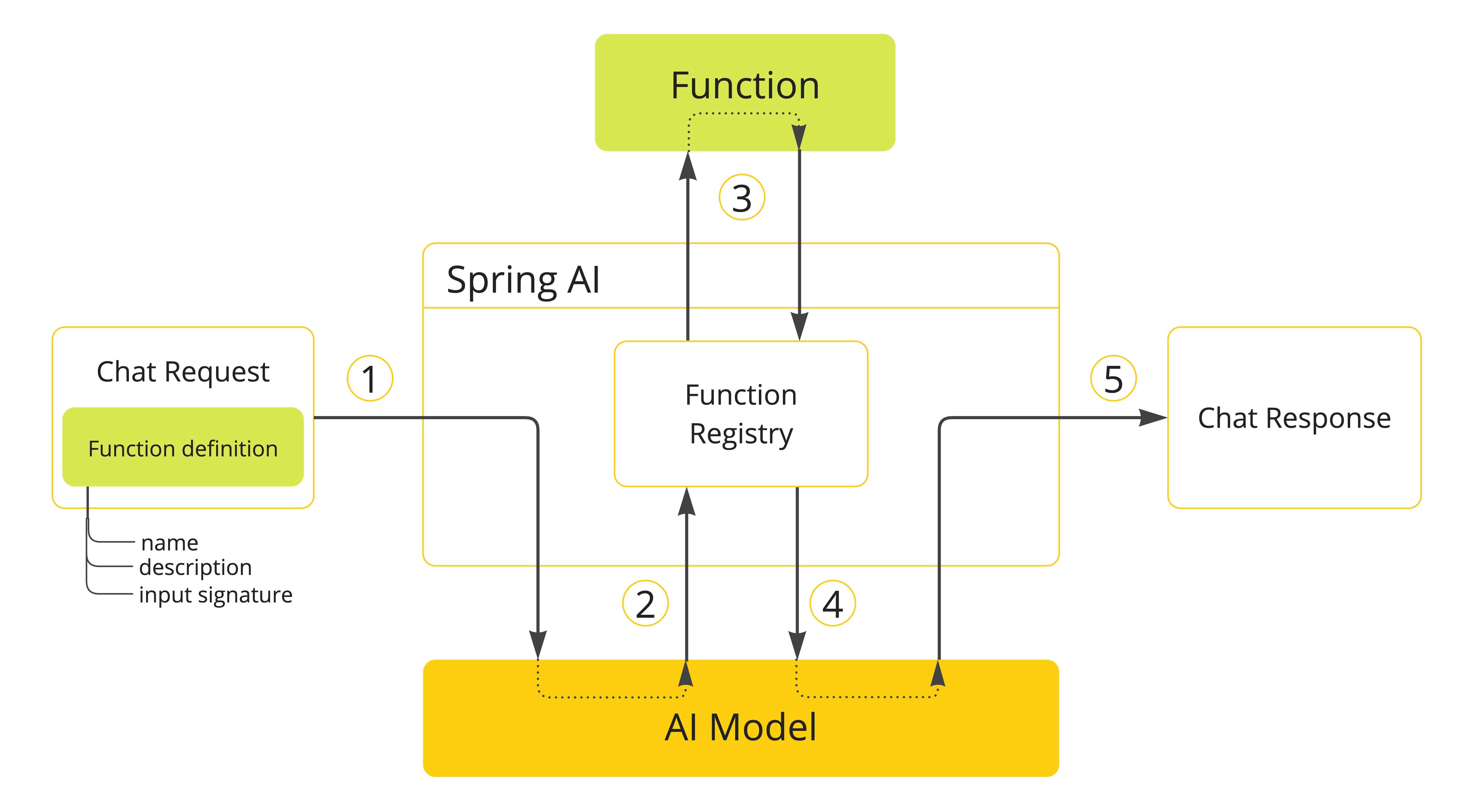
一起学Spring AI:核心概念
人工智能概念 本节描述了 Spring AI 使用的核心概念。我们建议您仔细阅读,以理解 Spring AI 实现背后的思想。 模型(Models) 人工智能模型是设计用来处理和生成信息的算法,通常模仿人类的认知功能。通过从大型数据集中学习模式…...

Oracle业务用户的存储过程个数及行数统计
Oracle业务用户的存储过程个数及行数统计 统计所有业务用户存储过程的个数独立定义的存储过程定义在包里的存储过程统计所有业务用户存储过程的总行数独立定义的存储过程定义在包里的存储过程📖 对存储过程进行统计主要用到以下三个系统视图: dba_objects:记录了所有独立创…...

PicSharp(图片压缩工具) v1.1.6
PicSharp 一个简单、高效、灵活的跨平台桌面图像压缩应用程序。软件基于Rust实现,高性能低资源,能快速扫描文件或目录,批处理图像。软件还具备组合压缩策略,TinyPNG提供最佳压缩比,但需要互联网连接,对大量…...

前端文件下载常用方式详解
在前端开发中,实现文件下载是常见的需求。根据不同的场景,我们可以选择不同的方法来实现文件流的下载。本文介绍三种常用的文件下载方式: 使用 axios 发送 JSON 请求下载文件流使用 axios 发送 FormData 请求下载文件流使用原生 form 表单提…...
