信息最大化(Information Maximization)
信息最大化在目标域无标签的域自适应任务中,它迫使模型在没有真实标签的情况下,对未标记数据产生高置信度且类别均衡的预测。此外,这些预测也可以作为伪标签用于自训练。
例如,在目标域没有标签时,信息最大化损失可以应用于目标域数据,使模型适应目标域并产生有意义的预测,缓解源域和目标域之间的分布偏移。在自训练或生成模型中,信息最大化通过要求整体预测分布均衡,有效防止模型将所有样本都预测到少数几个类别上。
信息最大化损失函数
信息最大化的损失函数可以表达为[1]:
L I M = L e n t + L d i v = H ( Y ∣ X ) − H ( Y ) \begin{align} \mathcal{L}_{IM} &= \mathcal{L}_{ent}+\mathcal{L}_{div} \\ &= H(Y|X)-H(Y) \end{align} LIM=Lent+Ldiv=H(Y∣X)−H(Y)
式中, H ( Y ∣ X ) H(Y|X) H(Y∣X)模型预测输出标签的信息熵,最小化条件熵让模型的预测P(Y|X)更加自信。 H ( Y ) H(Y) H(Y)是预测类别标签的边缘熵,由于损失前面有个负号,则需要最大化边缘熵,迫使模型预测的各个类别均匀分布,而不是偏向其中某个类别。
信息最大化本质是最大化预测标签 Y Y Y 与输入 X X X 的互信息 I ( X ; Y ) = H ( Y ) − H ( Y ∣ X ) I(X;Y) = H(Y) - H(Y|X) I(X;Y)=H(Y)−H(Y∣X),因此 L I M = − I ( X ; Y ) \mathcal{L}_{IM} = -I(X;Y) LIM=−I(X;Y)。最小化该损失等价于提升输入与预测标签之间的互信息。
① 熵最小化损失 (Entropy Minimization):
L e n t = − E x ∑ c = 1 C δ c ( f ( x ) ) log δ c ( f ( x ) ) \begin{align} \mathcal{L}_{ent} = -\mathbb{E}_x \sum_{c=1}^C \delta_c(f(x)) \log \delta_c(f(x)) \end{align} Lent=−Exc=1∑Cδc(f(x))logδc(f(x))
式中, f ( x ) f(x) f(x)表示模型的预测输出, δ c \delta_c δc是softmax函数,代表样本 x x x是类别 c c c的概率值。
② 多样性最大化损失 (Diversity Regularization):
L d i v = − ( − ∑ c = 1 C p ^ c log p ^ c ) = ∑ c = 1 C p ^ c log p ^ c \begin{align} \mathcal{L}_{div} &=-(- \sum_{c=1}^C \hat{p}_c \log \hat{p}_c)\\ &= \sum_{c=1}^C \hat{p}_c \log \hat{p}_c \end{align} Ldiv=−(−c=1∑Cp^clogp^c)=c=1∑Cp^clogp^c
其中, p ^ c = 1 N ∑ i = 1 N p i c \hat{p}_c=\frac{1}{N}\sum_{i=1}^{N}p_{ic} p^c=N1∑i=1Npic表示类别 c c c在整个批次上的平均预测概率,也就是类别 c c c的边缘分布。注意:在数学上, P ( Y = c ) P(Y=c) P(Y=c)的边缘概率应该为 P ( Y = c ) = ∑ i = 1 N P ( X = x i , Y = c ) P(Y = c) = \sum_{i=1}^N P(X = x_i, Y = c) P(Y=c)=∑i=1NP(X=xi,Y=c),这里采用的均值而非总和,即采用批次均值 p ^ c \hat{p}_c p^c 作为无偏估计。
总结:
- 最小化条件熵 H ( Y ∣ X ) H(Y|X) H(Y∣X):迫使模型对每个目标域样本做出确定性预测。
- 最大化边缘熵 H ( Y ) H(Y) H(Y):确保模型在整个目标域上的预测类别分布均匀,防止坍缩到少数类。
代码
import torch
import torch.nn as nn
import torch.nn.functional as Fclass IMLoss(nn.Module):def __init__(self, lambda_div=0.1, eps=1e-8):"""信息最大化损失函数:无监督学习范式Args:lambda_div (float): 多样性损失的权重系数,默认0.1eps (float): 数值稳定项,防止log(0),默认1e-8"""super().__init__()self.lambda_div = lambda_divself.eps = epsdef forward(self, logits):"""计算信息最大化损失Args:logits (torch.Tensor): 模型输出的logits张量,形状为(batch_size, num_classes)Returns:torch.Tensor: 计算得到的总损失值"""# 计算softmax概率probs = F.softmax(logits, dim=1)# 1. L_ent: 熵最小化损失,使预测更确定entropy_per_sample = -torch.sum(probs * torch.log(probs + self.eps), dim=1)entropy_loss = torch.mean(entropy_per_sample)# 2. L_div: 多样性最大化损失, 使类别分布均匀mean_probs = torch.mean(probs, dim=0) # 边缘分布,由于样本是独立同分布的,这里考虑概率的平均值而非总和diversity_loss = -torch.sum(mean_probs * torch.log(mean_probs + self.eps))# L_IM总损失total_loss = entropy_loss - self.lambda_div * diversity_lossreturn total_lossnum_classes=3
bs=2logits = torch.randn(bs, num_classes) # 模型输出的逻辑值:model(x)
loss_fn = IMLoss()
loss = loss_fn(logits)
知识点
边缘分布/边际分布 (Marginal distribution)定义[2]:Given a known joint distribution of two discrete random variables, say, X X X and Y Y Y, the marginal distribution of either variable – X X X for example – is the probability distribution of X X X when the values of Y Y Y are not taken into consideration.
p X ( x i ) = ∑ j p ( x i , y j ) , p Y ( y j ) = ∑ i p ( x i , y j ) p_X(x_i)=\sum_jp(x_i,y_j),\\ p_Y(y_j)=\sum_i p(x_i,y_j) pX(xi)=j∑p(xi,yj),pY(yj)=i∑p(xi,yj)
案例:
如下表所示,一个批次有3个样本,类别为4,对应的随机变量Y的边缘分布为最后一行。
| y 1 y_1 y1 | y 2 y_2 y2 | y 3 y_3 y3 | y 4 y_4 y4 | p X ( x ) p_X(x) pX(x) | |
|---|---|---|---|---|---|
| x 1 x_1 x1 | 4 32 \frac{4}{32} 324 | 2 32 \frac{2}{32} 322 | 1 32 \frac{1}{32} 321 | 1 32 \frac{1}{32} 321 | 8 32 \frac{8}{32} 328 |
| x 2 x_2 x2 | 3 32 \frac{3}{32} 323 | 6 32 \frac{6}{32} 326 | 3 32 \frac{3}{32} 323 | 3 32 \frac{3}{32} 323 | 15 32 \frac{15}{32} 3215 |
| x 3 x_3 x3 | 9 32 \frac{9}{32} 329 | 0 0 0 | 0 0 0 | 0 0 0 | 9 32 \frac{9}{32} 329 |
| p Y ( y ) p_Y(y) pY(y) | 16 32 \frac{16}{32} 3216 | 8 32 \frac{8}{32} 328 | 4 32 \frac{4}{32} 324 | 4 32 \frac{4}{32} 324 | 32 32 \frac{32}{32} 3232 |
参考:
[1] [2002.08546] Do We Really Need to Access the Source Data? Source Hypothesis Transfer for Unsupervised Domain Adaptation
[2] Marginal distribution - Wikipedia
相关文章:
)
信息最大化(Information Maximization)
信息最大化在目标域无标签的域自适应任务中,它迫使模型在没有真实标签的情况下,对未标记数据产生高置信度且类别均衡的预测。此外,这些预测也可以作为伪标签用于自训练。 例如,在目标域没有标签时,信息最大化损失可以…...

整数的字典序怎么算
在Python中,字典序(lexicographical order)通常指的是按照字符串的字典顺序进行比较或排序。对于整数来说,字典序可以理解为将整数转换为字符串后进行比较的顺序。 计算整数的字典序 要计算整数的字典序,可以按照以下…...

知识拓展卡————————关于Access、Trunk、Hybrid端口
目录 什么是Trunk List、VLAN ID、PVID: VLAN ID(Virtual Local Area Network Identifier): Trunk List(Trunk列表): PVID(Prot VLAN ID): 关于Native VLAN &#x…...

AUTOSAR实战教程--DoIP_02_诊断链路建立流程
第一步:DoIP实体车辆声明/诊断仪车辆识别请求 打开激活线以后,DoIP实体发的三帧车辆声明报文。其中包含了DoIP实体的诊断逻辑地址(可以类比DoCAN的物理请求/响应地址),对应车辆的VIN码(若已配置࿰…...
音频剪辑软件少之又少好用
我们平时见到的图片以及视频编辑工具非常多,但是音频剪辑软件却是少之又少,更不用说有没有好用的,今天,给大家带来一款非常专业的音频剪辑软件,而且是会员喔。 软件简介 一款手机号登录即可以享受会员的超专业音频剪…...

客户端和服务器已成功建立 TCP 连接【输出解析】
文章目录 图片**1. 连接状态解析****第一条记录(服务器监听)****第二条记录(客户端 → 服务器)****第三条记录(服务器 → 客户端)** **2. 关键概念澄清****(1) 0.0.0.0 的含义****(2) 端口号的分配规则** *…...

多标签多分类 用什么函数激活
在多标签多分类任务中,激活函数的选择需要根据任务特性和输出层的设计来决定。以下是常见的激活函数及其适用场景: 一、多标签分类任务的特点 每个样本可以属于多个类别(标签之间非互斥,例如一篇文章可能同时属于 “科技” 和 “…...

day26-计算机网络-4
1. tcp的11种状态 ss -ant -a 表示看所有状态 -n 表示不将ip解析为主机名 -t 表示tcp 1.1. closed状态(客户端、服务端) 客户端发起建立连接前的状态服务端启动服务前的状态 1.2. listen状态(服务端) 服务端软件运行的时候状…...

ngx_stream_geo_module在传输层实现高性能 IP Region 路由
一、模块定位与核心价值 层次:工作在 Stream (TCP/UDP) 层,和 ngx_http_geo_module 的 L7 语义互补。作用:基于客户端 IP 前缀 / 范围生成一个 Nginx 变量,可在后续 proxy_pass、map、limit_conn、access 等指令中使用࿰…...

国防科技大学计算机基础慕课课堂学习笔记
1.信息论 香农作为信息论的这个创始人,给出来了这个信息熵的计算方法,为我们现在的这个生活的很多领域奠定了基础,我第一次听说这个信息熵是在这个数学建模里面的理论学习中有关于这个:决策树的模型,在那个问题里面&a…...
【第七篇】 SpringBoot项目的热部署
简介 本文介绍了热部署(Hot Deployment)的概念、使用场景及在IDEA中的配置方法。热部署可在不重启应用的情况下动态更新代码,提升开发效率,适用于调试、微服务架构和自动化测试等场景。文章详细说明了热部署的实现步骤(…...
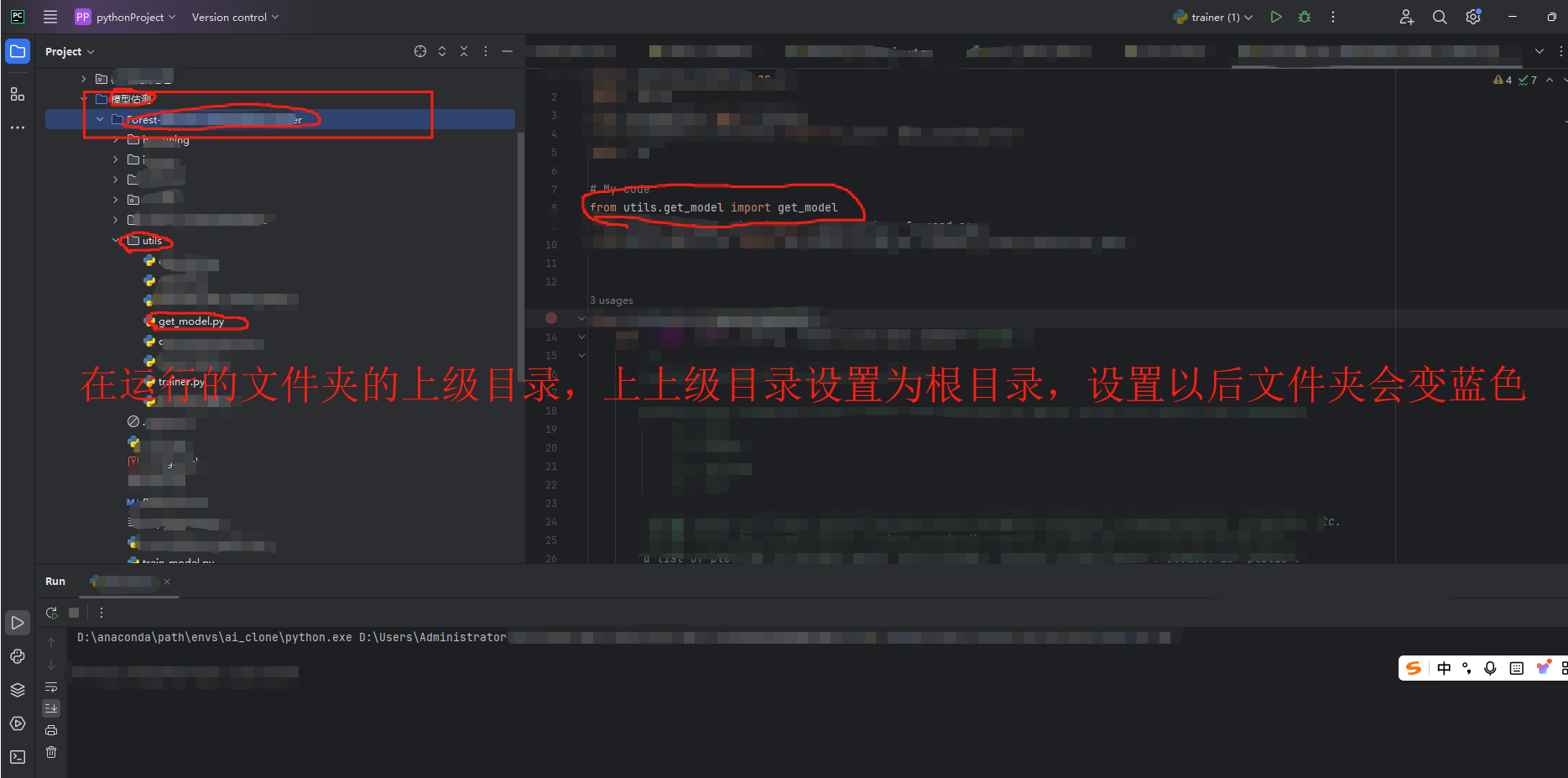
解决pycharm同一个文件夹下from *** import***仍显示No module named
1、,from ***import *,同文件夹中已有.py文件但是仍然报错No module named 原因是因为pycharm没有把文件夹设置为根目录,只需要在文件夹的上一级设置为根目录即可,测试过如果仅仅将当前的文件夹设置仍然报错,如果把最上…...
)
GO 基础语法和数据类型面试题及参考答案(上)
目录 Go 中变量定义方式有哪些?各有什么适用场景? 使用 : 定义变量的限制是什么? 全局变量可以使用 : 声明吗?为什么? Go 中如何声明一个多变量赋值?有哪些注意事项? 常量能否通过表达式赋值…...

使用 Redisson 实现分布式锁—解决方案详解
Redisson 是 Redis 官方推荐的 Java 客户端,提供了一系列分布式服务实现,其中分布式锁是其核心功能之一。本文将深入解析 Redisson 分布式锁的实现原理、高级特性和最佳实践。 一、Redisson 分布式锁的优势 与传统实现的对比 特性手动实现Redisson 实现…...

结合三维基因建模与智能体技术打造工业软件无码平台
通过深度整合 Protocol Buffers (Protobuf)、gRPC 及 Microsoft AI 技术,构建面向智能制造的高性能、智能化 PLM 平台。 一、Protocol Buffers 深度集成 1. 基因模型标准化定义 三维基因容器 Protobuf 规范: protobuf syntax "proto3"; pa…...

Python Day46
Task: 1.不同CNN层的特征图:不同通道的特征图 2.什么是注意力:注意力家族,类似于动物园,都是不同的模块,好不好试了才知道。 3.通道注意力:模型的定义和插入的位置 4.通道注意力后的特征图和热力…...

基于PostGIS的各地级市路网长度统计及Echarts图表可视化实践-以湖南省为例
目录 前言 一、路网长度计算 1、地级市列表查询 2、地级市路网长度查询 二、Echarts可视化实现 1、Echarts后端生成 2、引入Colormap配色 3、前端微调 三、总结 前言 在当今快速发展的社会中,交通路网的建设与布局对于一个地区的经济发展、居民生活以及城市…...

mac版excel如何制作时长版环形图
设置辅助列 创建簇状柱形图 将辅助列绘制在次坐标轴 工作时长在主坐标轴,右键分别更改图表类型为圆环。 辅助列圆环全部为灰色,边框为白色 辅助列设置透明度100% 设置辅助列和工作时长列同样的圆环大小 可得 核心:只要辅助列边框不透明…...
)
PCB设计教程【大师篇】——STM32开发板原理图设计(电源部分)
前言 本教程基于B站Expert电子实验室的PCB设计教学的整理,为个人学习记录,旨在帮助PCB设计新手入门。所有内容仅作学习交流使用,无任何商业目的。若涉及侵权,请随时联系,将会立即处理 目录 前言 1. 工程创建与前期…...

k8s4部署
configMap configmap概述:数据会存储在etcd数据库,其应用场景主要在应用程序的配置 configmap支持的类型(1)键值对(2)多行数据 pod使用configmap资源有两种常见的方式(1)变量注入&a…...
)
贝叶斯医学分析中“先验”的如何进行选择(文献解读)
贝叶斯医学分析中“先验”的如何进行选择(文献解读) 作者:Callum Taylor, Kathryn Puxty, Tara Quasim, Martin Shaw 文章标题:Understanding Bayesian analysis of clinical trials: an overview for clinicians 期刊名称&#x…...

【汇编逆向系列】七、函数调用包含多个参数之浮点型- XMM0-3寄存器
目录 1. 汇编代码 1.1 debug编译 1.2 release编译 2. 汇编分析 2.1 浮点参数传递规则 2.2 栈帧rsp的变化时序 2.3 参数的访问逻辑 2.4 返回值XMM0寄存器 3. 汇编转化 3.1 Debug编译 3.2 Release 编译 3.3 C语言转化 1. 汇编代码 上一节介绍了整型的函数传参&#x…...

【MySQL系列】MySQL 执行 SQL 文件
博客目录 一、MySQL 执行 SQL 文件的常见场景二、MySQL 执行 SQL 文件的主要方法1. 使用 MySQL 命令行客户端2. 在 MySQL 交互界面中使用 source 命令3. 使用 MySQL Workbench 等图形化工具4. 使用编程语言接口 三、执行 SQL 文件时的注意事项1. 字符集问题2. 事务处理3. 错误处…...

论文MR-SVD
每个像素 7 个 FLOPs意思: FLOPs(浮点运算次数):衡量算法计算复杂度的指标,数值越小表示运算越高效。含义:对图像中每个像素进行处理时,仅需执行7 次浮点运算(如加减乘除等…...

Java 日期时间类全面解析
Java 日期时间类全面解析:从传统到现代的演进 一、发展历程概览 二、传统日期类(Java 8前) 1. java.util.Date - 日期表示类 Date now new Date(); // 当前日期时间 System.out.println(now); // Wed May 15 09:30:45 CST 2023// 特定时间…...

【工具-Wireshark 抓包工具】
工具-Wireshark 抓包工具 ■ Wireshark 抓包工具■ 通过IP指定查看■■ ■ Wireshark 抓包工具 抓包工具】win 10 / win 11:WireShark 下载、安装、使用 Wireshark下载 阿里云镜像 ■ 通过IP指定查看 ■ ■...

Linux安全机制:从SELinux到Intel SGX的堡垒
Linux安全机制:从SELinux到Intel SGX的堡垒 数字世界的钢铁长城 引言:操作系统的"防御工事" 当服务器每天承受数百万次攻击尝试时,Linux内核的安全机制如同精密的防御系统,在纳秒级时间内做出响应。现代Linux安全架构已…...

设备驱动与文件系统:06 目录与文件
磁盘使用的最后一层抽象:文件系统 今天我们讲第31讲,这一讲将完成磁盘对磁盘使用的最后一层抽象。对此板使用最后一层抽象,抽象出来的是什么呢? 实际上我们使用过磁盘,大家应该有这样的认识,最后不管这个磁…...
算法的锁无实现及应用)
C++11 Token Bucket (令牌桶)算法的锁无实现及应用
Token Bucket(令牌桶)算法是一种在流量控制和资源分配领域被广泛应用的技术。它通过约束数据传输速率或任务执行频率,确保系统在资源有限的情况下,能够稳定、高效地运行,避免因突发流量或任务积压而导致的性能下降甚至…...

详细介绍uni-app中Composition API和Options API的使用方法
uni-app 中 Composition API 和 Options API 的使用方法详解 一、Options API(Vue 2.x 传统方式) 1. 基本结构 Options API 通过配置对象的不同选项(如 data、methods、computed 等)组织代码: <template><…...
