2025年ESWA SCI1区TOP,自适应学习粒子群算法AEPSO+动态周期调节灰色模型,深度解析+性能实测
目录
- 1.摘要
- 2.粒子群算法PSO原理
- 3.改进策略
- 4.结果展示
- 5.参考文献
- 6.代码获取
- 7.算法辅导·应用定制·读者交流

1.摘要
能源数据的科学预测对于能源行业决策和国家经济发展具有重要意义,尤其是短期能源预测,其精度直接影响经济运行效率。为了更好地提高预测模型的精度,本文提出了一种自适应学习粒子群算法(AEPSO)用于优化灰色预测模型的参数,并通过引入正弦混沌机制、自适应引导觅食策略、随机维度学习策略以及自适应均值优化策略来提升原始算法的性能。
2.粒子群算法PSO原理
【智能算法】粒子群算法(PSO)原理及实现
3.改进策略
自适应导引觅食策略
自适应引导觅食策略通过引入方向切换向量,构建了三种飞行方式:全方向飞行、对角飞行和轴向飞行。
-
轴向飞行表示个体可以沿任意坐标轴方向飞行;
-
对角飞行表示个体可以从一个矩形角落飞到另一个角落;
-
全方向飞行表示个体的飞行方向可以映射到所有坐标轴方向。

轴向飞行:
D i = { 1 , i = r a n d i ( [ 1 , d ] ) , i = 1 , 2 , ⋯ , d 0 , e l s e \boldsymbol{D}_i=\left\{ \begin{array} {cc}1, & i=randi([1,d]),i=1,2,\cdots,d \\ 0, & else \end{array}\right. Di={1,0,i=randi([1,d]),i=1,2,⋯,delse
对角飞行:
D i = { 1 , i = P ( i ) , j ∈ [ 1 , k ] , P = r a n d p e r m ( k ) , k ∈ [ 2 , [ r 1 ∙ ( d − 2 ) ] + 1 ] 0 , e l s e \boldsymbol{D}_i=\left\{ \begin{array} {cc}1, & i=P(i),j\in[1,k],P=randperm(k),k\in[2,[r_1\bullet(d-2)]+1] \\ 0, & else \end{array}\right. Di={1,0,i=P(i),j∈[1,k],P=randperm(k),k∈[2,[r1∙(d−2)]+1]else
全方向飞行:
D i = 1 i = 1 , 2 , ⋯ , d D_i=1i=1,2,\cdots,d Di=1i=1,2,⋯,d
个体判断方向信息后更新速度:
V i ( t + 1 ) = w ∙ x i , t a r ( t ) + c 1 a 1 ∙ D ∙ ( x i ( t ) − x i , t a r ( t ) ) + c 2 a 2 ∙ ( x i ( t ) − x i n d e x ( t ) ) \begin{aligned} V_{i}(t+1) & =w\bullet x_{i,tar}(t)+c_{1}a_{1}\bullet D\bullet\left(x_{i}(t)-x_{i,tar}(t)\right)+c_{2}a_{2} \\ & \bullet\left(x_{i}(t)-x_{index}(t)\right) \end{aligned} Vi(t+1)=w∙xi,tar(t)+c1a1∙D∙(xi(t)−xi,tar(t))+c2a2∙(xi(t)−xindex(t))
随机维度学习策略
随机维度学习策略,使PSO不仅可以向全局最优个体学习,还可以从随机个体的部分维度中进行学习,从而增强搜索能力:
{ V i , p 1 ( t + 1 ) = x index , p 1 ( t ) + ( V i , p 1 ( t ) − x index , p 1 ( t ) ) ⋅ ( r 1 + 1 ) ⋅ sin ( r 2 ⋅ 360 ) V i , p 2 ( t + 1 ) = x index , p 2 ( t ) + ( V i , p 2 ( t ) − x index , p 2 ( t ) ) ⋅ ( r 1 + 1 ) ⋅ cos ( r 2 ⋅ 360 ) \begin{cases} V_{i,p_1}(t+1) = x_{\text{index},p_1}(t) + \left(V_{i,p_1}(t) - x_{\text{index},p_1}(t)\right) \cdot (r_1 + 1) \cdot \sin(r_2 \cdot 360) \\ V_{i,p_2}(t+1) = x_{\text{index},p_2}(t) + \left(V_{i,p_2}(t) - x_{\text{index},p_2}(t)\right) \cdot (r_1 + 1) \cdot \cos(r_2 \cdot 360) \end{cases} {Vi,p1(t+1)=xindex,p1(t)+(Vi,p1(t)−xindex,p1(t))⋅(r1+1)⋅sin(r2⋅360)Vi,p2(t+1)=xindex,p2(t)+(Vi,p2(t)−xindex,p2(t))⋅(r1+1)⋅cos(r2⋅360)
在更新位置信息之前先更新飞行方向,以帮助个体能够在最有效的路径上找到食物,并更新方向信息:
D i ( t + 1 ) = D i ( t ) + ( − P + 2 ∙ P ∙ r a n d ( 1 , D i m ) ) ∙ D i ( t ) \boldsymbol{D}_i(t+1)=\boldsymbol{D}_i(t)+(-P+2\bullet P\bullet rand(1,Dim))\bullet\boldsymbol{D}_i(t) Di(t+1)=Di(t)+(−P+2∙P∙rand(1,Dim))∙Di(t)
更新方向信息后,粒子的位置信息更新:
x i ( t + 1 ) = x i ( t ) + r a n d n ∙ x i ( t ) ∙ D i ( t ) x_i(t+1)=x_i(t)+randn\bullet x_i(t)\bullet D_i(t) xi(t+1)=xi(t)+randn∙xi(t)∙Di(t)
自适应均值优化策略
均值优化策略目标是缩小均值解与全局最优解之间的距离,使均值解在优化过程中持续向全局最优解靠近。
x i ( t + 1 ) = B i ( t ) + ( c ∙ z 1 + ( 1 − c ) ∙ z 2 ) − M ( t ) x_i(t+1)=B_i(t)+(c\bullet z_1+(1-c)\bullet z_2)-M(t) xi(t+1)=Bi(t)+(c∙z1+(1−c)∙z2)−M(t)



4.结果展示



PS:效果不好🤣🤣🤣
5.参考文献
[1] Hu G, Wang S, Shu B, et al. AEPSO: An adaptive learning particle swarm optimization for solving the hyperparameters of dynamic periodic regulation grey model[J]. Expert Systems with Applications, 2025: 127578.
6.代码获取
xx
7.算法辅导·应用定制·读者交流
相关文章:

2025年ESWA SCI1区TOP,自适应学习粒子群算法AEPSO+动态周期调节灰色模型,深度解析+性能实测
目录 1.摘要2.粒子群算法PSO原理3.改进策略4.结果展示5.参考文献6.代码获取7.算法辅导应用定制读者交流 1.摘要 能源数据的科学预测对于能源行业决策和国家经济发展具有重要意义,尤其是短期能源预测,其精度直接影响经济运行效率。为了更好地提高预测模型…...

LeetCode - 53. 最大子数组和
目录 题目 Kadane 算法核心思想 Kadane 算法的步骤分析 读者可能的错误写法 正确的写法 题目 53. 最大子数组和 - 力扣(LeetCode) Kadane 算法核心思想 定义状态变量: currentSum: 表示以当前元素为结束的子数组的最大和。 maxSum: 记录全局最大…...
)
稻米分类和病害检测数据集(猫脸码客第237期)
稻米分类图像数据集:驱动农业智能化发展的核心资源 引言 在全球农业体系中,稻米作为最关键的粮食作物之一,其品种多样性为人类饮食提供了丰富选择。然而,传统稻米分类方法高度依赖人工经验,存在效率低、主观性强等缺…...
深度解析)
DOM(文档对象模型)深度解析
DOM(文档对象模型)深度解析 DOM 是 HTML/XML 文档的树形结构表示,提供了一套让 JavaScript 动态操作网页内容、结构和样式的接口。 一、DOM 核心概念 1. 节点(Node)类型 类型值说明示例ELEMENT_NODE1元素节点<div>, <p>TEXT_NODE3文本节点元素内的文字COMMEN…...

四、Sqoop 导入表数据子集
作者:IvanCodes 日期:2025年6月4日 专栏:Sqoop教程 当不需要将关系型数据库中的整个表一次性导入,而是只需要表中的一部分数据时,Sqoop 提供了多种方式来实现数据子集的导入。这通常通过过滤条件或选择特定列来完成。 …...

【读代码】从预训练到后训练:解锁语言模型推理潜能——Xiaomi MiMo项目深度解析
项目开源地址:https://github.com/XiaomiMiMo/MiMo 一、基本介绍 Xiaomi MiMo是小米公司开源的7B参数规模语言模型系列,专为复杂推理任务设计。项目包含基础模型(MiMo-7B-Base)、监督微调模型(MiMo-7B-SFT)和强化学习模型(MiMo-7B-RL)等多个版本。其核心创新在于通过…...

DROPP算法详解:专为时间序列和空间数据优化的PCA降维方案
DROPP (Dimensionality Reduction for Ordered Points via PCA) 是一种专门针对有序数据的降维方法。本文将详细介绍该算法的理论基础、实现步骤以及在降维任务中的具体应用。 在现代数据分析中,高维数据集普遍存在特征数量庞大的问题。这种高维特性不仅增加了计算…...

DeepSeek11-Ollama + Open WebUI 搭建本地 RAG 知识库全流程指南
🛠️ Ollama Open WebUI 搭建本地 RAG 知识库全流程指南 💻 一、环境准备 # 1. 安装 Docker 和 Docker Compose sudo apt update && sudo apt install docker.io docker-compose -y# 2. 添加用户到 docker 组(避免 sudo 权限&…...

【AI大模型】Transformer架构到底是什么?
引言 —— 想象一台能瞬间读懂整本《战争与和平》、精准翻译俳句中的禅意、甚至为你的设计草图生成前端代码的机器——这一切并非科幻,而是过去七年AI领域最震撼的技术革命:Transformer架构创造的奇迹。 当谷歌在2017年揭开Transformer的神秘面纱时&…...

code-server安装使用,并配置frp反射域名访问
为什么使用 code-server是VSCode网页版开发软件,可以在浏览器访问编程,可以使用vscode中的插件。如果有自己的服务器,使用frp透传后,域名访问在线编程,使用方便,打开的服务端口不需要单独配置,可…...

MTK-Android12-13 Camera2 设置默认视频画质功能实现
MTK-Android12-13 Camera2 设置默认视频画质功能实现 场景:部分客户使用自己的mipi相机安装到我们主板上,最大分辨率为1280720,但是视频画质默认的是640480。实际场景中,在默认视频分辨率情况下拍出来的视频比较模糊、预览也不清晰…...
)
Kafka 消息模式实战:从简单队列到流处理(一)
一、Kafka 简介 ** Kafka 是一种分布式的、基于发布 / 订阅的消息系统,由 LinkedIn 公司开发,并于 2011 年开源,后来成为 Apache 基金会的顶级项目。它最初的设计目标是处理 LinkedIn 公司的海量数据,如用户活动跟踪、消息传递和…...
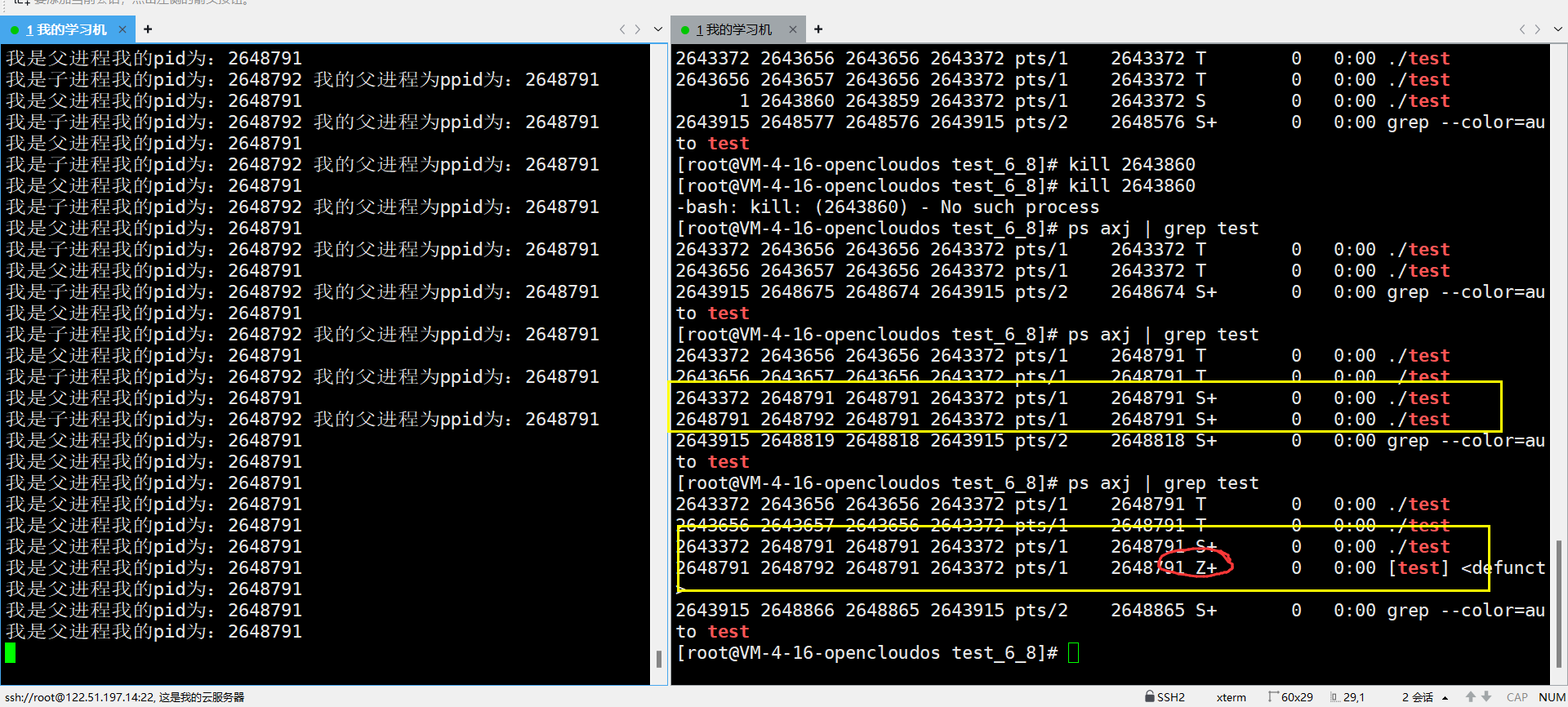
Linux知识回顾总结----进程状态
本章将会介绍进程的一些概念:冯诺伊曼体系结构、进程是什么,怎么用、怎么表现得、进程空间地址、物理地址、虚拟地址、为什么存在进程空间地址、如何感性得去理解进程空间地址、环境变量是如何使用的。 目录 1. 冯诺伊曼体系结构 1.1 是什么 1.2 结论 …...

Linux 进程管理学习指南:架构、计划与关键问题全解
Linux 进程管理学习指南:架构、计划与关键问题全解 本文面向初学者,旨在帮助你从架构视角理解 Linux 进程管理子系统,构建系统化学习路径,并通过结构化笔记方法与典型问题总结,夯实基础、明确方向,逐步掌握…...
)
【异常】极端事件的概率衰减方式(指数幂律衰减)
在日常事件中,极端事件的概率衰减方式并非单一模式,而是取决于具体情境和数据生成机制。以下是科学依据和不同衰减形式的分析: 1. 指数衰减(Exponential Decay) 典型场景:当事件服从高斯分布(正态分布)或指数分布时,极端事件的概率呈指数衰减。 数学形式:概率密度函数…...

Git 使用大全:从入门到精通
Git 是目前最流行的分布式版本控制系统,被广泛应用于软件开发中。本文将全面介绍 Git 的各种功能和使用方法,包含大量代码示例和实践建议。 文章目录 Git 基础概念版本控制系统Git 的特点Git 的三个区域Git 文件状态 Git 安装与配置安装 GitLinuxmacOSWi…...

奈飞工厂官网,国内Netflix影视在线看|中文网页电脑版入口
奈飞工厂是一个专注于提供免费Netflix影视资源的在线播放平台,致力于为国内用户提供的Netflix热门影视内容。该平台的资源与Netflix官网基本同步,涵盖电影、电视剧、动漫和综艺等多个领域。奈飞工厂的界面简洁流畅,资源分类清晰,方…...

Python基于蒙特卡罗方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融投资中,风险管理是确保资产安全和实现稳健收益的关键环节。随着市场波动性的增加,传统…...

【bat win系统自动运行脚本-双击启动docker及其它】
win系统自动化运行脚本 创建一个 startup.bat右键编辑,输入以下示例 echo off start "" "C:\Program Files\Docker\Docker\Docker Desktop.exe"timeout /t 5docker start your_container_namestart cmd /k "conda activate your_conda_e…...

SpringBoot离线应用的5种实现方式
在当今高度依赖网络的环境中,离线应用的价值日益凸显。无论是在网络不稳定的区域运行的现场系统,还是需要在断网环境下使用的企业内部应用,具备离线工作能力已成为许多应用的必备特性。 本文将介绍基于SpringBoot实现离线应用的5种不同方式。…...

js 比较两个对象的值,不相等就push对象的key
在JavaScript中,比较两个对象(object)的值并找出不相等的key,可以通过多种方法实现。下面是一些常用的方法: 方法1:使用JSON.stringify 这种方法适用于简单的对象,其中对象的值是基本类型或可…...

SQL 注入开放与修复
开发: SQL 注入是一种数据库攻击手段。攻击者通过向应用程序提交恶意代码来改变原 SQL 语句的含义, 进而执行任意 SQL 命令,达到入侵数据库乃至操作系统的目的。 例如:下面代码片段中,动态构造并执行了一个 SQ…...

【学习记录】Office 和 WPS 文档密码破解实战
文章目录 📌 引言📁 Office 与 WPS 支持的常见文件格式Microsoft Office 格式WPS Office 格式 🛠 所需工具下载地址(Windows 官方编译版)🔐 破解流程详解步骤 1:提取文档的加密哈希值步骤 2&…...

AGV|无人叉车工业语音播报器|预警提示器LBE-LEX系列性能与接线说明
LBE-LEX系列AGV|无人叉车工业语音播报器|预警提示器,涵盖LBE-LEI-M-00、LBE-LESM-00、LBE-LES-M-01、LBE-LEC-M-00、LBE-KEI-M-00、LBE-KES-M-00、LBE-KES-M-01、LBE-KEC-M-00等型号,适用于各种需要语音提示的场景,主要有AGV、AMR机器人、无人…...

【电路笔记】-变压器电压调节
变压器电压调节 文章目录 变压器电压调节1、概述2、变压器电压调节3、变压器电压调节示例14、变压器电压调节示例25、变压器电压调节示例36、总结变压器电压调节是变压器输出端电压因连接负载电流的变化而从其空载值向上或向下变化的比率或百分比值。 1、概述 电压调节是衡量变…...

多层PCB技术解析:从材料选型到制造工艺的深度实践
在电子设备集成度与信号传输要求不断提升的背景下,多层PCB凭借分层布局优势,成为高速通信、汽车电子、工业控制等领域的核心载体。其通过导电层、绝缘层的交替堆叠,实现复杂电路的立体化设计,显著提升空间利用率与信号完整性。 一…...

(33)课54:3 张表的 join-on 连接举例,多表查询总结。数据库编程补述及游标综合例题。静态 sqL与动态sqL(可带参数)
(112)3 张表的 join-on 连接举例 : (113) 多表查询总结 : (114)数据库编程补述 : 综合例题 : 以上没有动手练习,不知道这样的语法是否…...

Vue3 hooks
export default function(){ let name; function getName(){ return name; } return {name,getName} } use it ----------------------------------------------- import useName from hooks/useName const {name,getName} useName(); 这段代码展示了一个自定义 Vue3钩…...
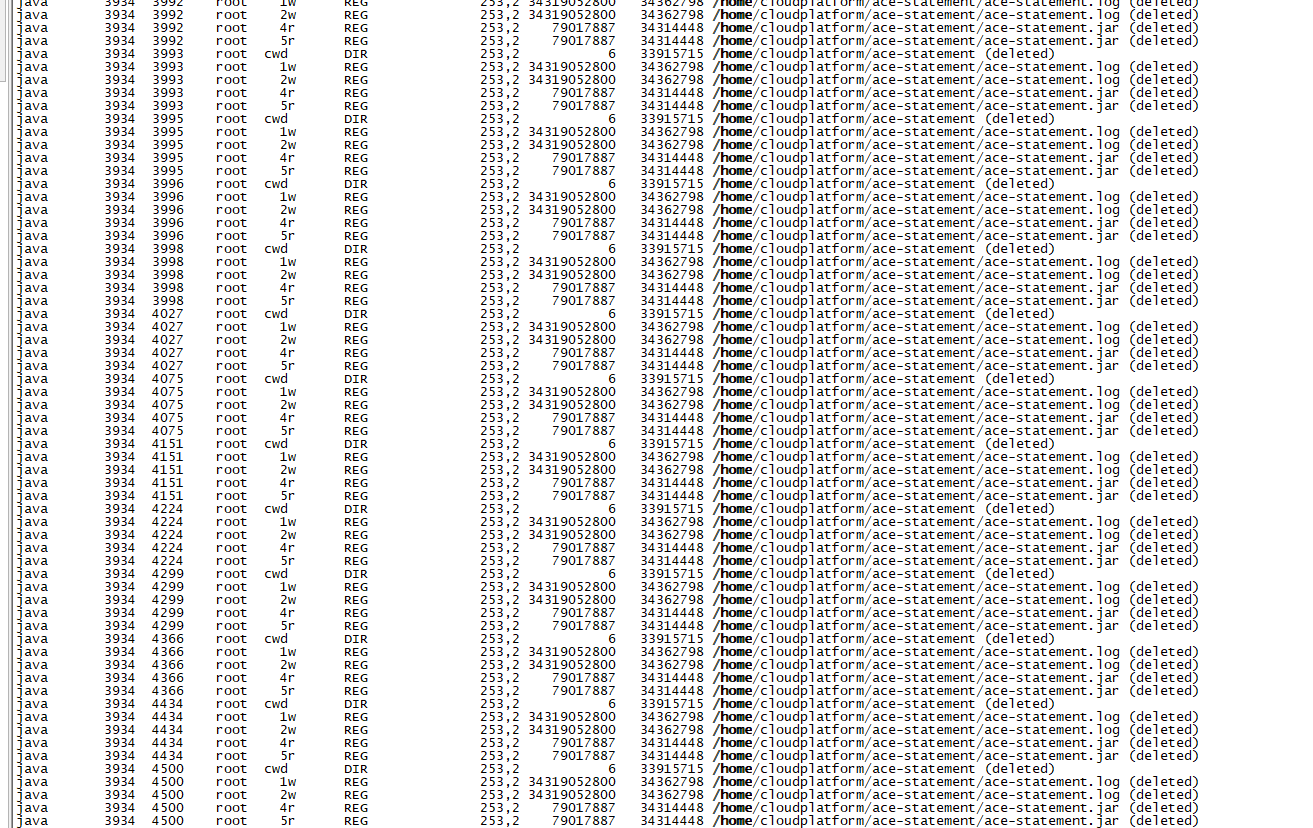
centos挂载目录满但实际未满引发系统宕机
测试服务器应用系统突然挂了,经过排查发现是因为磁盘“满了”导致的,使用df -h查看磁盘使用情况/home目录使用率已经到了100%,但使用du -sh /home查看发现实际磁盘使用还不到1G,推测有进程正在写入或占用已删除的大文件(Linux 系统…...

KKCMS部署
目录 账号 网站目录 快看CMS使用手册 http://10.141.19.241/kkcms/install/ 常规思路:页面点点观察url变化,参数 常规思路:点一个功能模块抓包看什么东西,正确是什么样,错误的是什么样,构造参数。 账号…...
