MeanFlow:何凯明新作,单步去噪图像生成新SOTA
1.简介
这篇文章介绍了一种名为MeanFlow的新型生成模型框架,旨在通过单步生成过程高效地将先验分布转换为数据分布。文章的核心创新在于引入了平均速度的概念,这一概念的引入使得模型能够通过单次函数评估完成从先验分布到数据分布的转换,显著提高了生成效率。
文章通过一系列实验验证了MeanFlow模型的性能,展示了其在单步生成任务中的强大能力,特别是在ImageNet 256×256数据集上的表现,显著优于以往的单步扩散/流模型。此外,文章还探讨了MeanFlow模型在分类器自由引导(CFG)方面的应用,通过自然地整合CFG,进一步提升了生成质量,同时保持了单步生成的高效性。这些创新不仅为生成模型的研究提供了新的视角,也为实际应用中的高效数据生成提供了有力的支持。

效果图

github地址:GitHub - haidog-yaqub/MeanFlow: Pytorch Implementation (unofficial) of the paper "Mean Flows for One-step Generative Modeling" by Geng et al.
论文地址:https://arxiv.org/pdf/2505.13447
-
-
2.论文详解
Flow Matching
Flow Matching是一类生成模型,旨在学习匹配两个概率分布之间的流,这些流由速度场表示。具体来说:
- 给定数据
和先验
,可以构造一个随时间 t 变化的流路径
,其中
和
是预先定义的时间表。
- 速度
定义为
,其中 ' 表示时间导数。这种速度在作者的研究中被称为条件速度,记作
。通常使用的时间表是
和
,带入上式后
。
这里的 ϵ 通常表示噪声。在生成模型的上下文中,噪声 ϵ 是一个随机变量,用于引入随机性,从而生成多样化的样本。具体来说,ϵ 通常是从某个预定义的概率分布(如标准正态分布)中采样得到的,这个分布被称为先验分布
。

-
左图(Conditional flows):展示了条件流。给定一个中间状态 zt,它可以由不同的原始数据 x 和噪声 ϵ 对产生,这导致不同的条件速度 vt。图中用不同颜色的箭头表示不同的速度向量。
-
右图(Marginal flows):展示了边际流,这是通过对所有可能的条件速度进行边缘化(即对所有可能的 x 和 ϵ 进行平均)得到的。边际速度场作为网络训练的基础真实场。图中展示了这个速度场,它是由所有条件流的平均速度构成的。
这张图实际上在说明这样一件事:
- 左图表示所有
和x的匹配结果(多个流匹配路径),可见同一个
可以和多个x进行匹配,这又将导致不同的
,即条件速度。左图的箭头实际上表示一个
可能有多个流匹配的移动方向
。
- 而右图表示的是:Flow Matching本质上建模的是所有可能性的期望(也就是将所有可能的条件速度
求平均),作者称之为边际速度:
。而流匹配其实是多个流匹配路径的平均值。

-
接下来作者使用一个由参数 参数化的神经网络
来拟合边际速度场,其损失函数定义为
。尽管由于上式中的边际化操作,直接计算这个损失函数是不可行的,但作者提出可以转而评估条件Flow Matching损失:
,其中目标
是条件速度。最小化
等价于最小化
。详细解释如下:
LFM(θ) 是通过计算神经网络预测的速度场 vθ(zt,t) 与真实的边际速度场 v(zt,t) 之间的差异来定义的。
LCFM(θ) 是通过计算神经网络预测的速度场 vθ(zt,t) 与给定条件下的真实速度场 vt(zt∣x) 之间的差异来定义的。
由于边际速度场是所有条件速度的平均值,最小化 LCFM 实际上是在最小化所有条件速度的平均误差。这意味着,如果我们能够准确地拟合每个条件下的速度场,那么边际速度场也会被准确地拟合。
给定一个边际速度场,可以通过解
的常微分方程(ODE)来生成样本:
从
开始。这个解可以写成:
,其中作者用 r 表示另一个时间步。在实践中,这个积分是在离散的时间步上通过数值方法来近似的。例如欧拉方法(一种一阶ODE求解器),也可以应用更高阶的求解器。
值得注意的是,尽管每个单独的条件流(条件速度)可能是直线,但因为边际速度是多个速度的平均值,即当考虑所有可能的条件流时,平均下来后的整体轨迹可能会变得弯曲。
-
MeanFlow模型
(本章数学公式过于硬核,请做好准备)
作者的方法的核心思想是引入一个新的场来表示平均速度,而在Flow Matching中建模的速度表示瞬时速度。
平均速度:作者将平均速度定义为两个时间步长 t 和 r 之间的位移(通过积分获得)除以时间间隔。形式上,平均速度 u 定义为:

-
瞬时速度 v:决定了路径的切线方向,即数据点在某一时刻的瞬时运动方向。
-
平均速度 u(z,r,t):与位移对齐,反映了数据点在一段时间内的平均运动趋势,通常与瞬时速度不一致。
-
位移:定义为 (t−r)u(z,r,t),表示数据点在一段时间内的平均位移。

为了强调概念上的区别,作者在整篇论文中使用符号 u 来表示平均速度,使用 v 来表示瞬时速度。 是一个同时依赖于 (r, t) 的场。 u 的场在图3中进行了说明。需要注意的是,通常情况下,平均速度 u 是瞬时速度 v 的一个泛函的结果:即
。平均速度 u 是由瞬时速度 v 诱导的场,不依赖于任何神经网络。这意味着 u 是一个客观存在的场,与模型的实现无关。
作者的MeanFlow模型的最终目标是使用神经网络 来近似平均速度。这有一个显著的优势,即假设我们能够准确近似这个量,我们可以通过
的单次评估来近似整个流路径。换句话说,这种方法更适合单步或少步生成。
然而,直接使用定义的平均速度作为训练网络的真实值是不可行的,因为这需要在训练期间评估一个积分。作者的关键洞见是,平均速度的定义方程可以被操作以构建一个最终适合训练的优化目标,即使只有瞬时速度是可访问的。
MeanFlow恒等式
为了得到一个适合训练的公式,作者将方程重写为:
现在作者对两边关于 t 求导,将 r 视为与 t 独立的变量。这导致:
其中左边的操作使用了乘积法则,而右边使用了微积分的基本定理。重新排列项,作者得到了恒等式:

作者将这个方程称为“MeanFlow恒等式”,它描述了 v 和 u 之间的关系。方程的右边为 提供了一个“目标”形式,作者将利用它来构建一个损失函数以训练神经网络。为了作为一个合适的目标,我们还必须进一步分解时间导数项,作者接下来将讨论这一点。
计算时间导数
为了计算方程中的 项,注意
表示一个全导数,它可以在偏导数的条件下展开:
由于,
,和
,作者得到了 u 和 v 之间的另一个关系:
这个方程表明,总导数是由函数 u 的雅可比矩阵 和切向量
之间的雅可比向量积(JVP)给出的。在现代库中,这可以通过 jvp 接口高效计算,例如 PyTorch 中的 torch.func.jvp 或 JAX 中的 jax.jvp。
使用平均速度进行训练
到目前为止,公式不依赖于任何网络参数化。现在作者引入一个模型来学习 u。形式上,作者参数化一个网络 并鼓励它满足MeanFlow恒等式。具体来说,作者最小化以下目标:
,其中
该目标使用瞬时速度 v 作为唯一的真实信号;不需要积分计算。虽然目标应该涉及 u 的导数(即 ),但它们被其参数化对应物(即
)替换。在损失函数中,应用了停止梯度(sg)操作到目标
。

这个算法1实际上是:使用模型预测u,而真实值u_tgt不好算,然后进行了一系列的转换,转换为v和dudt的表达式,然后计算得到u_tgt,然后利用预测值u和真实值u_tgt计算损失。
相应的,推理过程如下:

-
有CFG的MeanFlow
作者的方法自然支持无分类器引导(CFG)。
真实场
作者构建了一个新的真实场 :
(13)
这是一个类别条件场和类别无条件场的线性组合:
其中 是条件速度(更准确地说,是样本条件速度)。遵循MeanFlow的精神,作者引入了与
对应的平均速度
。根据MeanFlow恒等式,
满足:
(15)
再次, 和
是不依赖于神经网络的底层真实场。这里,如方程(13)中定义的
,可以重写为:
(16)
其中作者利用了关系:,以及
。
使用引导进行训练
通过方程(15)和方程(16),作者构建了一个网络及其学习目标。作者直接通过函数 参数化
。
基于方程(15),作者得到目标:(17),其中
这个公式类似于方程(9),唯一的区别是它有一个修改后的 :
(19)
这是由方程(16)驱动的:方程(16)中的 项,即边际速度,被(样本条件)速度
替换,如果
,这个损失函数退化为方程(9)中的无CFG情况。
为了使方程(17)中的网络 暴露于类别无条件输入,作者以10%的概率丢弃类别条件。出于类似的动机,作者也可以在方程(19)中将
暴露于类别无条件和类别条件版本。
带有CFG的单步NFE采样
在作者的公式中, 直接模拟
,这是由CFG速度
(方程(13))引起的平均速度。因此,在采样过程中不需要线性组合:作者直接使用
进行单步采样(见算法2),仅需要一次NFE。这种公式保留了理想的单步NFE行为。
-
其他
损失
作者考虑损失函数的形式为 ,其中
表示回归误差。可以证明,最小化
等价于最小化平方L2损失
并使用“自适应损失权重”。详细信息见附录。在实践中,作者设置权重为
,其中
且 c > 0(例如,
)。自适应加权损失是
,其中
。如果 p = 0.5,这类似于Pseudo-Huber损失。
采样时间步 (r, t)
作者从预定分布中采样两个时间步 (r, t)。作者研究了两种类型的分布:(i)均匀分布,,和(ii)对数正态(lognorm)分布,其中样本首先从正态分布
中抽取,然后使用逻辑函数映射到 (0, 1)。给定一个采样对,作者将较大的值分配给 t,较小的值分配给 r。作者设置一定比例的随机样本,使得 r = t。
在 (r, t) 上的条件化
作者使用位置嵌入来编码时间变量,然后将它们组合并提供给神经网络作为条件。作者注意到,尽管场由 参数化,但网络不必直接条件化 (r, t)。例如,作者可以让网络直接条件化
,其中
。在这种情况下,作者有
,其中 net 是网络。JVP计算总是相对于函数
。作者在实验中比较不同的条件形式。
-
实验
表1展示了作者在ImageNet 256×256数据集上进行的消融研究结果,主要关注单步生成(1-NFE)的性能,使用Fréchet Inception Distance(FID)作为评估指标。表1中的消融研究验证了MeanFlow模型中各个组件的有效性,并展示了如何通过调整不同的参数来优化模型性能。

图4展示了MeanFlow模型在ImageNet 256×256数据集上的可扩展性研究结果。具体来说,图中展示了不同模型大小(从B/2到XL/2)和不同训练周期下,使用1-NFE(单步函数评估)生成的Fréchet Inception Distance(FID)分数。

表2比较了在ImageNet 256×256数据集上不同生成模型的性能,主要使用Fréchet Inception Distance(FID)作为评估指标。 表2展示了MeanFlow模型在单步和少步生成任务中的竞争力,特别是在1-NFE生成上取得了最先进的性能。

3.代码详解
train.py
这段代码实现了一个训练循环,主要功能如下:
- 使用 `tqdm` 显示训练进度条;
- 从数据加载器中获取图像和类别标签,送入指定设备(如GPU);
- 前向传播计算损失(重要),进行反向传播和优化;
- 每隔一定步骤记录损失值、学习率等到日志文件;
- 每隔一定步骤生成样本图像并保存。
这段代码我们不多介绍
with tqdm(range(n_steps), dynamic_ncols=True) as pbar:pbar.set_description("Training")model.train()for step in pbar:data = next(train_dataloader)x = data[0].to(accelerator.device) # 图像 [b,c,h,w]=[48,1,32,32](mnist)c = data[1].to(accelerator.device) # 类别 bloss, mse_val = meanflow.loss(model, x, c) # 计算损失accelerator.backward(loss) # 反向传播optimizer.step() # 更新参数optimizer.zero_grad() # 梯度清零global_step += 1 # 记录训练状态losses += loss.item()mse_losses += mse_val.item()if accelerator.is_main_process:if global_step % log_step == 0: # 每隔一定步骤(log_step)在主进程中记录训练日志信息到文件。current_time = time.asctime(time.localtime(time.time()))batch_info = f'Global Step: {global_step}'loss_info = f'Loss: {losses / log_step:.6f} MSE_Loss: {mse_losses / log_step:.6f}'# Extract the learning rate from the optimizerlr = optimizer.param_groups[0]['lr']lr_info = f'Learning Rate: {lr:.6f}'log_message = f'{current_time}\n{batch_info} {loss_info} {lr_info}\n'with open('log.txt', mode='a') as n:n.write(log_message)losses = 0.0mse_losses = 0.0if global_step % sample_step == 0:if accelerator.is_main_process:model_module = model.module if hasattr(model, 'module') else modelz = meanflow.sample_each_class(model_module, 1)log_img = make_grid(z, nrow=10)img_save_path = f"images/step_{global_step}.png"save_image(log_img, img_save_path)accelerator.wait_for_everyone()model.train()其中最重要的部分是loss, mse_val = meanflow.loss(model, x, c),我们接下来进行介绍
-
meanflow.py
代码的核心部分位于meanflow.py下
MeanFlow.loss()函数实现了一个基于扩散模型的训练损失计算,主要包括以下步骤:
- 时间采样:生成时间对 `(t, r)` 用于控制扩散过程;
- 噪声与归一化:加入随机噪声 `e` 并对输入 `x` 归一化;
- 插值与速度构造:构建中间状态 `z` 和目标方向 `v`;
- CFG增强:使用无条件模型输出进行分类器无关引导(Classifier-Free Guidance);
- JVP计算:通过雅可比向量积计算模型输出及其时间导数;
- 目标构建与误差计算:构建目标 `u_tgt` 并计算误差;
- 损失计算:使用自适应 L2 损失函数 [adaptive_l2_loss]
class MeanFlow:def __init__():...self.normer = Normalizer.from_list(normalizer)if jvp_api == 'funtorch':self.jvp_fn = torch.func.jvpself.create_graph = Falseelif jvp_api == 'autograd':self.jvp_fn = torch.autograd.functional.jvpself.create_graph = Truedef loss(self, model, x, c=None):batch_size = x.shape[0]device = x.devicet, r = self.sample_t_r(batch_size, device) # 该函数用于生成时间对 (t, r),其中 t 表示较大的时间值,r 表示较小的时间值,并以一定比例让 r 等于 t。t_ = rearrange(t, "b -> b 1 1 1") # [b,1,1,1]r_ = rearrange(r, "b -> b 1 1 1")e = torch.randn_like(x) # 生成噪声 e [b,c,h,w]=[48,1,32,32]x = self.normer.norm(x) # 对输入 x 进行归一化z = (1 - t_) * x + t_ * e # 插值变量 z [b,c,h,w]=[48,1,32,32]v = e - x # 条件速度v_t [b,c,h,w]=[48,1,32,32]if self.w is not None: # 使用无条件分支进行 CFG(Classifier-Free Guidance)增强uncond = torch.ones_like(c) * self.num_classes # [b],内部全是10with torch.no_grad():u_t = model(z, t, t, uncond)v_hat = self.w * v + (1 - self.w) * u_t # 构造 v_hat 作为目标方向。else:v_hat = v# 以一定概率self.cfg_ratio将输入c中的元素替换为无条件输入uncondcfg_mask = torch.rand_like(c.float()) < self.cfg_ratioc = torch.where(cfg_mask, uncond, c)if self.cfg_uncond == 'v':# as v = wv - (1-w)v = wv - (1-w)u in the unconditional case, should we directly use v instead?cfg_mask = rearrange(r, "b -> b 1 1 1").bool()v_hat = torch.where(cfg_mask, v, v_hat)# forward pass# u = model(z, t, r, y=c)model_partial = partial(model, y=c) # model_partial 是固定了部分参数(y=c)后的模型函数jvp_args = ( # 雅可比矩阵向量积(JVP)的参数元组 jvp_argslambda z, t, r: model_partial(z, t, r),(z, t, r),(v_hat, torch.ones_like(t), torch.zeros_like(r)),)if self.create_graph:u, dudt = self.jvp_fn(*jvp_args, create_graph=True) # 调用jvp_fn得到输出u和其时间导数dudtelse:u, dudt = self.jvp_fn(*jvp_args)u_tgt = v_hat - (t_ - r_) * dudt # 目标值u_tgterror = u - stopgrad(u_tgt) # 计算当前输出 u 与目标输出 u_tgt 的误差loss = adaptive_l2_loss(error) # 对误差使用自适应 L2 损失函数计算最终损失。# loss = F.mse_loss(u, stopgrad(u_tgt))mse_val = (stopgrad(error) ** 2).mean()return loss, mse_val其中sample_t_r()如下,用于生成满足特定分布的时间对 (t, r),其中 t >= r。
- 根据设定的分布类型(uniform 或 lognorm)生成两列随机数;
- 将每行较大的值作为 t,较小的作为 r;
- 按照一定比例(flow_ratio)将部分样本的 r 设为等于 t;
def sample_t_r(self, batch_size, device):if self.time_dist[0] == 'uniform': # 根据分布类型(uniform)生成两列随机数samples = np.random.rand(batch_size, 2).astype(np.float32)elif self.time_dist[0] == 'lognorm': # 根据分布类型(lognorm)生成两列随机数mu, sigma = self.time_dist[-2], self.time_dist[-1]normal_samples = np.random.randn(batch_size, 2).astype(np.float32) * sigma + mu # [b,2]samples = 1 / (1 + np.exp(-normal_samples)) # 应用 sigmoid# 每行的两个数中较大者为 t,较小者为 r Assign t = max, r = min, for each pairt_np = np.maximum(samples[:, 0], samples[:, 1]) #r_np = np.minimum(samples[:, 0], samples[:, 1])# 按照 flow_ratio 概率随机选取部分样本,使这些样本的 r = t;num_selected = int(self.flow_ratio * batch_size)indices = np.random.permutation(batch_size)[:num_selected]r_np[indices] = t_np[indices]t = torch.tensor(t_np, device=device)r = torch.tensor(r_np, device=device)return t, r其中对输入 `x` 归一化是使用Normalizer.norm()
class Normalizer:def __init__(self, mode='minmax', mean=None, std=None):...self.mode = modeif mode == 'mean_std':if mean is None or std is None:raise ValueError("mean and std must be provided for 'mean_std' mode")self.mean = torch.tensor(mean).view(-1, 1, 1)self.std = torch.tensor(std).view(-1, 1, 1)def norm(self, x):if self.mode == 'minmax':return x * 2 - 1elif self.mode == 'mean_std':return (x - self.mean.to(x.device)) / self.std.to(x.device)其中loss如下:
传统的 L2 损失(MSE)对于大误差非常敏感,容易被 outliers 影响。而这个损失函数通过引入一个基于误差大小的动态权重来降低大误差的影响,从而达到以下效果:
- 对小误差保持近似 L2 特性(平滑、易优化)
- 对大误差自动降低权重,防止其主导训练过程
,其中
stopgrad() 是为了防止权重
w在反向传播中影响梯度计算。换句话说,w是根据当前误差计算出来的,但它本身不参与梯度更新,只是作为加权系数使用。这样可以保证训练稳定性。
def adaptive_l2_loss(error, gamma=0.5, c=1e-3):"""Adaptive L2 loss: sg(w) * ||Δ||_2^2, where w = 1 / (||Δ||^2 + c)^p, p = 1 - γArgs:error: Tensor of shape (B, C, W, H)gamma: Power used in original ||Δ||^{2γ} lossc: Small constant for stabilityReturns:Scalar loss"""delta_sq = torch.mean(error ** 2, dim=(1, 2, 3), keepdim=False) # 计算每个样本的均方误差[b]p = 1.0 - gamma # p = 1 - γw = 1.0 / (delta_sq + c).pow(p) # w = 1 / (||Δ||^2 + c)^p, p = 1 - γloss = delta_sq # ||Δ||^2 return (stopgrad(w) * loss).mean() # 使用 stopgrad(w) 阻止权重梯度传播 sg(w) * ||Δ||_2^2该函数用于在给定模型和类别条件下,为每个类别生成指定数量的图像样本。
class MeanFlow:@torch.no_grad() # 禁用梯度计算def sample_each_class(self, model, n_per_class,sample_steps=1, device='cuda'):model.eval()c = torch.arange(self.num_classes, device=device).repeat(n_per_class) # [c] 创建类别标签张量,每个类重复n_per_class次z = torch.randn(self.num_classes * n_per_class, self.channels,self.image_size, self.image_size, device=device) # 初始化随机噪声图像。[c,channel,h,w]=[10,1,32,32]t = torch.ones((c.shape[0],), device=c.device) # 定义固定的时间步t和参考步rr = torch.zeros((c.shape[0],), device=c.device)z = z - model(z, t, r, c) # 使用模型对噪声进行一次去噪操作 [c,channel,h,w]=[10,1,32,32]z = self.normer.unnorm(z.clip(-1, 1)) # 将图像从归一化空间还原到原始像素空间。 [c,channel,h,w]=[10,1,32,32]return z其中unnorm()如下:用于将图像从归一化空间还原到原始像素空间。
class Normalizer:def unnorm(self, x):if self.mode == 'minmax':return (x + 1) * 0.5elif self.mode == 'mean_std':return x * self.std.to(x.device) + self.mean.to(x.device)-
模型架构
模型架构就是基本的dit架构,即是一个条件扩散模型的时间感知 Transformer 主干网络(Conditional Diffusion Transformer),其主要作用是:在给定噪声图像 x、扩散时间步 t、参考信息 r 和可选类别标签 y 的情况下,预测去噪后的图像残差。
class MFDiT(nn.Module):def __init__():...self.x_embedder = PatchEmbed(input_size, patch_size, in_channels, dim)self.t_embedder = TimestepEmbedder(dim)self.r_embedder = TimestepEmbedder(dim)self.y_embedder = LabelEmbedder(num_classes, dim) if self.use_cond else Noneself.pos_embed = nn.Parameter(torch.zeros(1, num_patches, dim), requires_grad=True)self.blocks = nn.ModuleList([DiTBlock(dim, num_heads, mlp_ratio) for _ in range(depth)])self.final_layer = FinalLayer(dim, patch_size, self.out_channels)self.initialize_weights()def initialize_weights(self):# Initialize transformer layers:def _basic_init(module):if isinstance(module, nn.Linear):torch.nn.init.xavier_uniform_(module.weight)if module.bias is not None:nn.init.constant_(module.bias, 0)self.apply(_basic_init)# Initialize (and freeze) pos_embed by sin-cos embedding:pos_embed = get_2d_sincos_pos_embed(self.pos_embed.shape[-1], int(self.x_embedder.num_patches ** 0.5))self.pos_embed.data.copy_(torch.from_numpy(pos_embed).float().unsqueeze(0))# Initialize patch_embed like nn.Linear (instead of nn.Conv2d):w = self.x_embedder.proj.weight.datann.init.xavier_uniform_(w.view([w.shape[0], -1]))nn.init.constant_(self.x_embedder.proj.bias, 0)# Initialize label embedding table:if self.y_embedder is not None:nn.init.normal_(self.y_embedder.embedding.weight, std=0.02)# Initialize timestep embedding MLP:nn.init.normal_(self.t_embedder.mlp[0].weight, std=0.02)nn.init.normal_(self.t_embedder.mlp[2].weight, std=0.02)# Zero-out adaLN modulation layers in DiT blocks:for block in self.blocks:nn.init.constant_(block.adaLN_modulation[-1].weight, 0)nn.init.constant_(block.adaLN_modulation[-1].bias, 0)# Zero-out output layers:nn.init.constant_(self.final_layer.adaLN_modulation[-1].weight, 0)nn.init.constant_(self.final_layer.adaLN_modulation[-1].bias, 0)nn.init.constant_(self.final_layer.linear.weight, 0)nn.init.constant_(self.final_layer.linear.bias, 0)def unpatchify(self, x):"""x: (N, T, patch_size**2 * C)imgs: (N, H, W, C)"""c = self.out_channelsp = self.x_embedder.patch_size[0] # 2h = w = int(x.shape[1] ** 0.5) # 16assert h * w == x.shape[1]x = x.reshape(shape=(x.shape[0], h, w, p, p, c)) # [b,16,16,2,2,1]x = torch.einsum('nhwpqc->nchpwq', x)imgs = x.reshape(shape=(x.shape[0], c, h * p, h * p)) # [b,1,32,32]return imgsdef forward(self, x, t, r, y=None):"""Forward pass of DiT.x: (N, C, H, W) tensor of spatial inputs (images or latent representations of images)t: (N,) tensor of diffusion timestepsy: (N,) tensor of class labels"""H, W = x.shape[-2:]x = self.x_embedder(x) + self.pos_embed # 将输入图像 x 通过 x_embedder 转换为嵌入表示,并加上位置编码 [b,t,d]=[48,256,384] (N, T, D), where T = H * W / patch_size ** 2t = self.t_embedder(t) # (N, D)=[48,384]r = self.r_embedder(r)# t = torch.cat([t, r], dim=-1)t = t + r # 时间与参考嵌入:分别对 t 和 r 进行嵌入后相加# condition 得到条件向量 cc = tif self.use_cond: # 类别条件融合y = self.y_embedder(y) # (N, D)c = c + y # (N, D)for i, block in enumerate(self.blocks):x = block(x, c) # (N, T, D)x = self.final_layer(x, c) # (N, T, patch_size ** 2 * out_channels)=[48,256,4]x = self.unpatchify(x) # 还原为图像格式 (N, out_channels, H, W)return xclass DiTBlock(nn.Module):def __init__(self, dim, num_heads, mlp_ratio=4.0):super().__init__()self.norm1 = RMSNorm(dim)self.attn = Attention(dim, num_heads=num_heads, qkv_bias=True, qk_norm=True, norm_layer=RMSNorm)self.attn.fused_attn = Falseself.norm2 = RMSNorm(dim)mlp_dim = int(dim * mlp_ratio)approx_gelu = lambda: nn.GELU(approximate="tanh")self.mlp = Mlp(in_features=dim, hidden_features=mlp_dim, act_layer=approx_gelu, drop=0)self.adaLN_modulation = nn.Sequential(nn.SiLU(), nn.Linear(dim, 6 * dim))def forward(self, x, c):shift_msa, scale_msa, gate_msa, shift_mlp, scale_mlp, gate_mlp = (self.adaLN_modulation(c).chunk(6, dim=-1) # [b,d]=[48,384] 通过 adaLN_modulation 从条件输入 c 中生成六个仿射变换参数(平移和缩放)及门控系数)x = x + gate_msa.unsqueeze(1) * self.attn( # [b,t,d]=[48,256,384] 进行仿射变换,再通过注意力机制,并乘以门控系数后残差连接modulate(self.norm1(x), scale_msa, shift_msa))x = x + gate_mlp.unsqueeze(1) * self.mlp( # [b,t,d]=[48,256,384]modulate(self.norm2(x), scale_mlp, shift_mlp) # 进行仿射变换后通过 MLP,并乘以门控系数后残差连接)return x其中
def modulate(x, scale, shift):return x * (1 + scale.unsqueeze(1)) + shift.unsqueeze(1)-
-
4.总结
这篇文章介绍了MeanFlow,这是一种新型的一步生成模型框架,用于生成建模。与传统的流匹配方法不同,MeanFlow通过引入平均速度的概念来表征流场,而不是使用瞬时速度。平均速度定义为两个时间步长之间的位移与时间间隔的比值,这一定义使得模型能够在单次函数评估中完成从先验分布到数据分布的转换,显著提高了生成效率。文章详细阐述了MeanFlow模型的理论基础,包括平均速度与瞬时速度之间的关系,以及如何通过神经网络训练来近似平均速度场。此外,文章还探讨了如何将分类器自由引导(CFG)整合到MeanFlow模型中,以进一步提升生成样本的质量,同时保持单步生成的高效性。通过在ImageNet 256×256数据集上的实验,作者展示了MeanFlow模型在一步生成任务中的优越性能,其生成的图像质量显著优于现有的一步扩散/流模型。文章的研究表明,MeanFlow模型不仅在理论上具有创新性,而且在实际应用中也展现出了巨大的潜力,为生成模型的研究和应用提供了新的方向。
亲爱的读者朋友们,
在这个信息爆炸的时代,您的每一次点赞、收藏和关注都是对我们最大的支持和鼓励。我们致力于分享最有价值的内容,希望能够在您的日常生活中带来一点点启发和帮助。
👍 点赞 —— 您的点赞是我们前进的动力,它告诉我们,我们的内容是有价值的,是能够触动您的心弦的。
💼 收藏 —— 您的收藏是对我们内容的认可,它意味着这些信息对您来说是有用的,是值得您在未来回顾和参考的。
👀 关注 —— 您的关注是对我们最大的信任,它让我们有机会持续为您提供更多高质量的内容,一起探索更多的可能性。
我们承诺,将继续努力,不断优化和创新,为您带来更多有趣、有深度、有价值的内容。同时,我们也非常期待听到您的声音,无论是建议、反馈还是简单的交流,我们都将视为宝贵的财富。
让我们携手并进,共同成长。再次感谢您的支持,期待在未来的日子里,继续与您同行!
相关文章:
MeanFlow:何凯明新作,单步去噪图像生成新SOTA
1.简介 这篇文章介绍了一种名为MeanFlow的新型生成模型框架,旨在通过单步生成过程高效地将先验分布转换为数据分布。文章的核心创新在于引入了平均速度的概念,这一概念的引入使得模型能够通过单次函数评估完成从先验分布到数据分布的转换,显…...

【2D与3D SLAM中的扫描匹配算法全面解析】
引言 扫描匹配(Scan Matching)是同步定位与地图构建(SLAM)系统中的核心组件,它通过对齐连续的传感器观测数据来估计机器人的运动。本文将深入探讨2D和3D SLAM中的各种扫描匹配算法,包括数学原理、实现细节以及实际应用中的性能对比,特别关注…...

【Vue】scoped+组件通信+props校验
【scoped作用及原理】 【作用】 默认写在组件中style的样式会全局生效, 因此很容易造成多个组件之间的样式冲突问题 故而可以给组件加上scoped 属性, 令样式只作用于当前组件的标签 作用:防止不同vue组件样式污染 【原理】 给组件加上scoped 属性后…...
)
Docker环境下安装 Elasticsearch + IK 分词器 + Pinyin插件 + Kibana(适配7.10.1)
做RAG自己打算使用esmilvus自己开发一个,安装时好像网上没有比较新的安装方法,然后找了个旧的方法对应试试: 🚀 本文将手把手教你在 Docker 环境中部署 Elasticsearch 7.10.1 IK分词器 拼音插件 Kibana,适配中文搜索…...

第14节 Node.js 全局对象
JavaScript 中有一个特殊的对象,称为全局对象(Global Object),它及其所有属性都可以在程序的任何地方访问,即全局变量。 在浏览器 JavaScript 中,通常 window 是全局对象, 而 Node.js 中的全局…...

构建Docker镜像的Dockerfile文件详解
文章目录 前言Dockerfile 案例docker build1. 基本构建2. 指定 Dockerfile 路径3. 设置构建时变量4. 不使用缓存5. 删除中间容器6. 拉取最新基础镜像7. 静默输出完整示例 docker runDockerFile 入门syntax指定构造器FROM基础镜像RUN命令注释COPY复制ENV设置环境变量EXPOSE暴露端…...

Shell 解释器 bash 和 dash 区别
bash 和 dash 都是 Unix/Linux 系统中的 Shell 解释器,但它们在功能、语法和性能上有显著区别。以下是它们的详细对比: 1. 基本区别 特性bash (Bourne-Again SHell)dash (Debian Almquist SHell)来源G…...

从0开始学习R语言--Day17--Cox回归
Cox回归 在用医疗数据作分析时,最常见的是去预测某类病的患者的死亡率或预测他们的结局。但是我们得到的病人数据,往往会有很多的协变量,即使我们通过计算来减少指标对结果的影响,我们的数据中依然会有很多的协变量,且…...
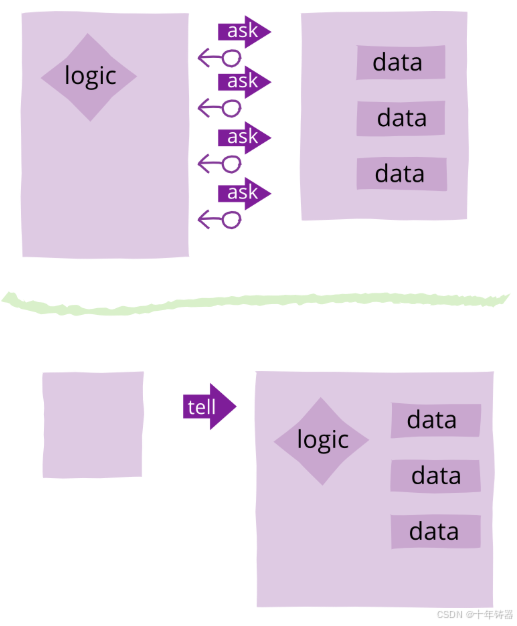
ABAP设计模式之---“Tell, Don’t Ask原则”
“Tell, Don’t Ask”是一种重要的面向对象编程设计原则,它强调的是对象之间如何有效地交流和协作。 1. 什么是 Tell, Don’t Ask 原则? 这个原则的核心思想是: “告诉一个对象该做什么,而不是询问一个对象的状态再对它作出决策。…...
——Oracle for Linux物理DG环境搭建(2))
Oracle实用参考(13)——Oracle for Linux物理DG环境搭建(2)
13.2. Oracle for Linux物理DG环境搭建 Oracle 数据库的DataGuard技术方案,业界也称为DG,其在数据库高可用、容灾及负载分离等方面,都有着非常广泛的应用,对此,前面相关章节已做过较为详尽的讲解,此处不再赘述。 需要说明的是, DG方案又分为物理DG和逻辑DG,两者的搭建…...

CentOS 7.9安装Nginx1.24.0时报 checking for LuaJIT 2.x ... not found
Nginx1.24编译时,报LuaJIT2.x错误, configuring additional modules adding module in /www/server/nginx/src/ngx_devel_kit ngx_devel_kit was configured adding module in /www/server/nginx/src/lua_nginx_module checking for LuaJIT 2.x ... not…...

IP选择注意事项
IP选择注意事项 MTP、FTP、EFUSE、EMEMORY选择时,需要考虑以下参数,然后确定后选择IP。 容量工作电压范围温度范围擦除、烧写速度/耗时读取所有bit的时间待机功耗擦写、烧写功耗面积所需要的mask layer...
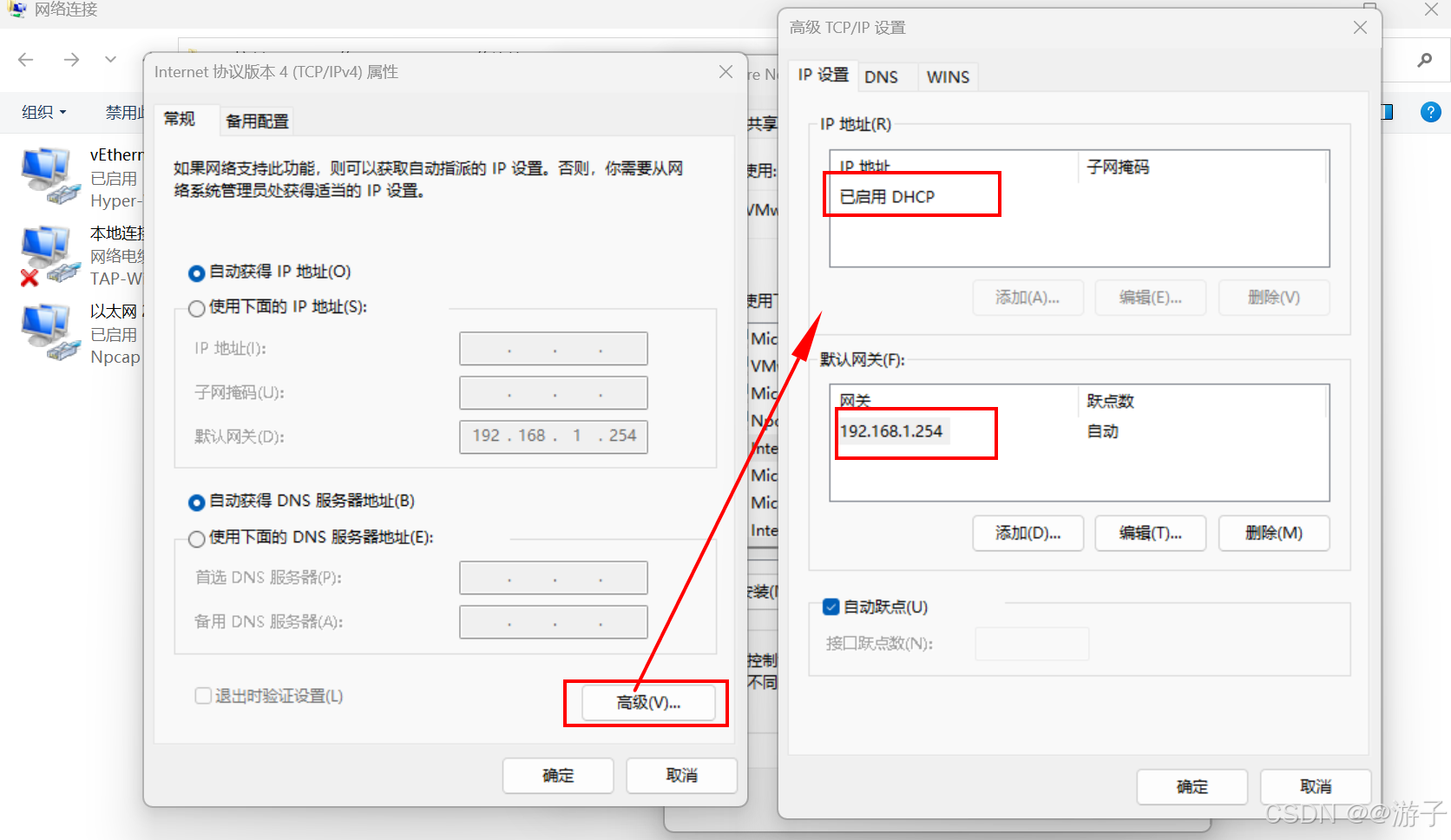
虚拟机网络不通的问题(这里以win10的问题为主,模式NAT)
当我们网关配置好了,DNS也配置好了,最后在虚拟机里还是无法访问百度的网址。 第一种情况: 我们先考虑一下,网关的IP是否和虚拟机编辑器里的IP一样不,如果不一样需要更改一下,因为我们访问百度需要从物理机…...

SOC-ESP32S3部分:30-I2S音频-麦克风扬声器驱动
飞书文档https://x509p6c8to.feishu.cn/wiki/SKZzwIRH3i7lsckUOlzcuJsdnVf I2S简介 I2S(Inter-Integrated Circuit Sound)是一种用于传输数字音频数据的通信协议,广泛应用于音频设备中。 ESP32-S3 包含 2 个 I2S 外设,通过配置…...

比较数据迁移后MySQL数据库和ClickHouse数据仓库中的表
设计一个MySQL数据库和Clickhouse数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

break 语句和 continue 语句
break语句和continue语句都具有跳转作用,可以让代码不按既有的顺序执行 break break语句用于跳出代码块或循环 1 2 3 4 5 6 for (var i 0; i < 5; i) { if (i 3){ break; } console.log(i); } continue continue语句用于立即终…...

使用 uv 工具快速部署并管理 vLLM 推理环境
uv:现代 Python 项目管理的高效助手 uv:Rust 驱动的 Python 包管理新时代 在部署大语言模型(LLM)推理服务时,vLLM 是一个备受关注的方案,具备高吞吐、低延迟和对 OpenAI API 的良好兼容性。为了提高部署效…...

更新 Docker 容器中的某一个文件
🔄 如何更新 Docker 容器中的某一个文件 以下是几种在 Docker 中更新单个文件的常用方法,适用于不同场景。 ✅ 方法一:使用 docker cp 拷贝文件到容器中(最简单) 🧰 命令格式: docker cp <…...
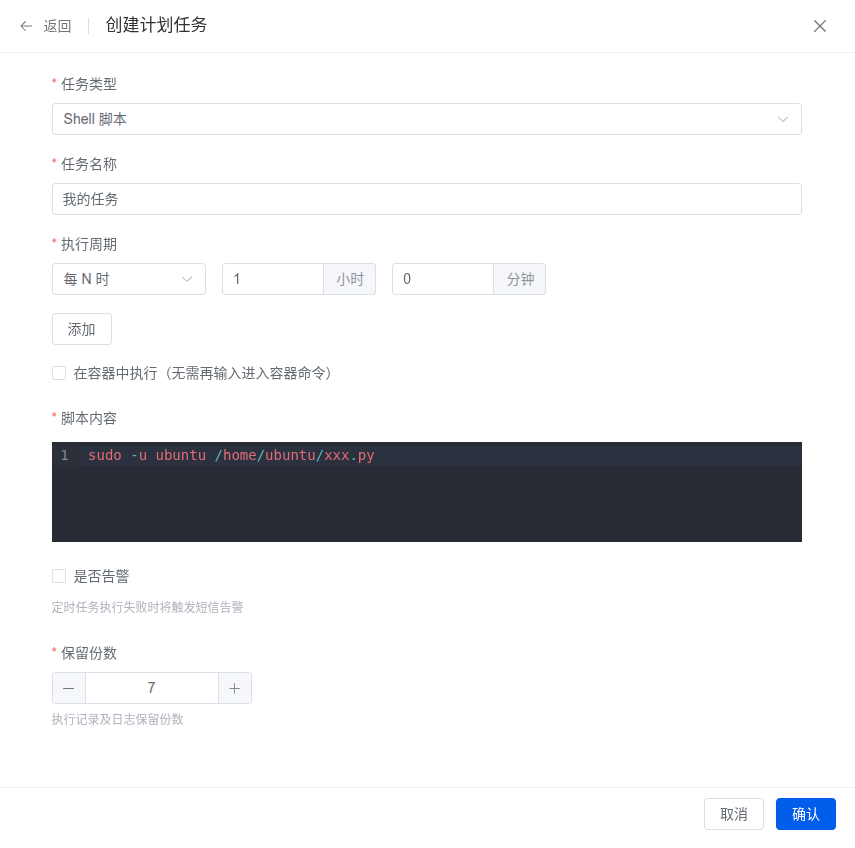
【Linux】使用1Panel 面板让服务器定时自动执行任务
服务器就是一台24小时开机的主机,相比自己家中不定时开关机的主机更适合完成定时任务,例如下载资源、备份上传,或者登录某个网站执行一些操作,只需要编写 脚本,然后让服务器定时来执行这个脚本就可以。 有很多方法实现…...
:PyQuery 框架)
Python爬虫(四):PyQuery 框架
PyQuery 框架详解与对比 BeautifulSoup 第一部分:PyQuery 框架介绍 1. PyQuery 是什么? PyQuery 是一个 Python 的 HTML/XML 解析库,它采用了 jQuery 的语法风格,让开发者能够用类似前端 jQuery 的方式处理文档解析。它的核心特…...

Excel 怎么让透视表以正常Excel表格形式显示
目录 1、创建数据透视表 2、设计 》报表布局 》以表格形式显示 3、设计 》分类汇总 》不显示分类汇总 1、创建数据透视表 2、设计 》报表布局 》以表格形式显示 3、设计 》分类汇总 》不显示分类汇总...
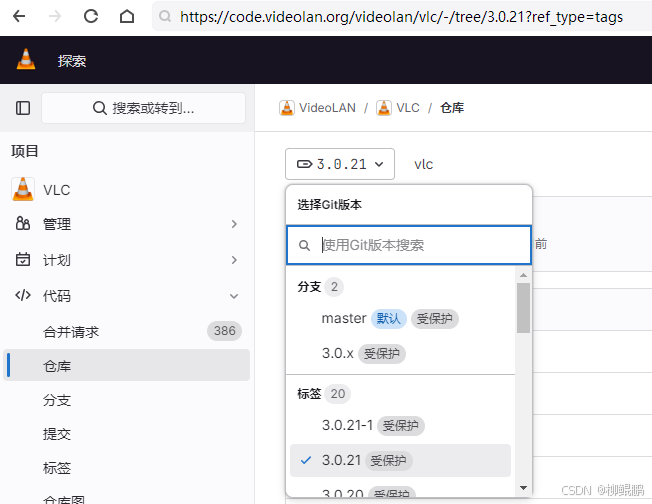
LINUX编译vlc
下载 VideoLAN / VLC GitLab 选择最新的发布版本 准备 sudo apt install -y xcb bison sudo apt install -y autopoint sudo apt install -y autoconf automake libtool编译ffmpeg LINUX FFMPEG编译汇总(最简化)_底部的附件列表中】: ffmpeg - lzip…...

初级程序员入门指南
初级程序员入门指南 在数字化浪潮中,编程已然成为极具价值的技能。对于渴望踏入程序员行列的新手而言,明晰入门路径与必备知识是开启征程的关键。本文将为初级程序员提供全面的入门指引。 一、明确学习方向 (一)编程语言抉择 编…...

WinUI3开发_使用mica效果
简介 Mica(云母)是Windows10/11上的一种现代化效果,是Windows10/11上所使用的Fluent Design(设计语言)里的一个效果,Windows10/11上所使用的Fluent Design皆旨在于打造一个人类、通用和真正感觉与 Windows 一样的设计。 WinUI3就是Windows10/11上的一个…...

Python爬虫(52)Scrapy-Redis分布式爬虫架构实战:IP代理池深度集成与跨地域数据采集
目录 一、引言:当爬虫遭遇"地域封锁"二、背景解析:分布式爬虫的两大技术挑战1. 传统Scrapy架构的局限性2. 地域限制的三种典型表现 三、架构设计:Scrapy-Redis 代理池的协同机制1. 分布式架构拓扑图2. 核心组件协同流程 四、技术实…...

MyBatis-Plus 常用条件构造方法
1.常用条件方法 方法 说明eq等于 ne不等于 <>gt大于 >ge大于等于 >lt小于 <le小于等于 <betweenBETWEEN 值1 AND 值2notBetweenNOT BETWEEN 值1 AND 值2likeLIKE %值%notLikeNOT LIKE %值%likeLeftLIKE %值likeRightLIKE 值%isNull字段 IS NULLisNotNull字段…...
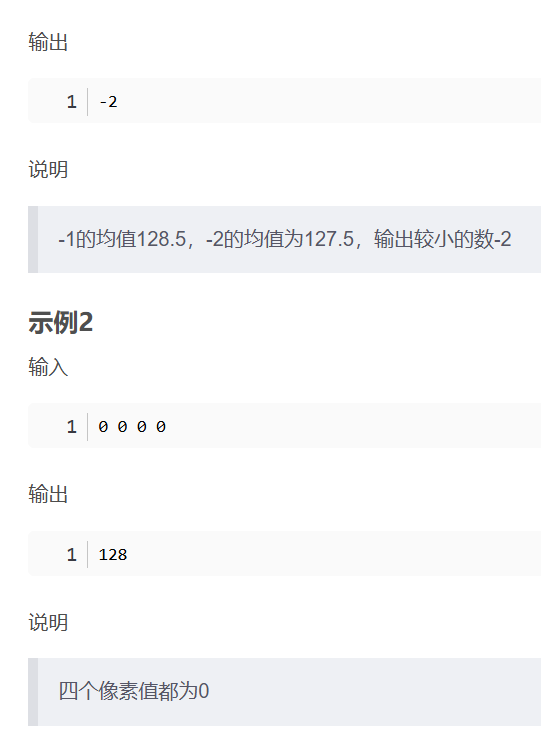
华为OD机考- 简单的自动曝光/平均像素
import java.util.Arrays; import java.util.Scanner;public class DemoTest4 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint[] arr Array…...

C/Python/Go示例 | Socket Programing与RPC
Socket Programming介绍 Computer networking这个领域围绕着两台电脑或者同一台电脑内的不同进程之间的数据传输和信息交流,会涉及到许多有意思的话题,诸如怎么确保对方能收到信息,怎么应对数据丢失、被污染或者顺序混乱,怎么提高…...

Spring是如何实现无代理对象的循环依赖
无代理对象的循环依赖 什么是循环依赖解决方案实现方式测试验证 引入代理对象的影响创建代理对象问题分析 源码见:mini-spring 什么是循环依赖 循环依赖是指在对象创建过程中,两个或多个对象相互依赖,导致创建过程陷入死循环。以下通过一个简…...

C++ Saucer 编写Windows桌面应用
文章目录 一、背景二、Saucer 简介核心特性典型应用场景 三、生成自己的项目四、以Win32项目方式构建Win32项目禁用最大化按钮 五、总结 一、背景 使用Saucer框架,开发Windows桌面应用,把一个html页面作为GUI设计放到Saucer里,隐藏掉运行时弹…...
