用js实现常见排序算法
以下是几种常见排序算法的 JS实现,包括选择排序、冒泡排序、插入排序、快速排序和归并排序,以及每种算法的特点和复杂度分析
1. 选择排序(Selection Sort)
核心思想:每次从未排序部分选择最小元素,与未排序部分的第一个元素交换。
function selectionSort(arr) {const n = arr.length;for (let i = 0; i < n - 1; i++) {let minIndex = i;// 找到未排序部分的最小元素索引for (let j = i + 1; j < n; j++) {if (arr[j] < arr[minIndex]) {minIndex = j;}}// 交换最小元素到当前位置if (minIndex !== i) {[arr[i], arr[minIndex]] = [arr[minIndex], arr[i]];}}return arr;
}
特点:
- 时间复杂度:O(n²),无论数据分布如何。
- 空间复杂度:O(1),原地排序。
- 稳定性:不稳定(例如
[5, 5, 2]排序后第一个 5 可能被交换到第二个 5 之后)。
2. 冒泡排序(Bubble Sort)
核心思想:多次遍历数组,比较相邻元素并交换,将最大元素“冒泡”到末尾。
function bubbleSort(arr) {const n = arr.length;for (let i = 0; i < n - 1; i++) {let swapped = false;for (let j = 0; j < n - i - 1; j++) {if (arr[j] > arr[j + 1]) {[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];swapped = true;}}// 如果没有交换,说明数组已排序,提前退出if (!swapped) break;}return arr;
}
特点:
- 时间复杂度:O(n²),优化后最好情况为 O(n)(数据已排序)。
- 空间复杂度:O(1),原地排序。
- 稳定性:稳定(相同元素的相对顺序不变)。
3. 插入排序(Insertion Sort)
核心思想:将未排序数据插入已排序序列的合适位置。
function insertionSort(arr) {const n = arr.length;for (let i = 1; i < n; i++) {const current = arr[i];let j = i - 1;// 将大于current的元素后移while (j >= 0 && arr[j] > current) {arr[j + 1] = arr[j];j--;}// 插入currentarr[j + 1] = current;}return arr;
}
特点:
- 时间复杂度:O(n²),最好情况为 O(n)(数据接近有序)。
- 空间复杂度:O(1),原地排序。
- 稳定性:稳定。
- 适用场景:小规模数据或部分有序数据。
4. 快速排序(Quick Sort)
核心思想:分治法,选择基准值,将数组分为两部分,递归排序。
function quickSort(arr) {if (arr.length <= 1) return arr;const pivot = arr[0]; // 选择第一个元素为基准const left = [];const right = [];for (let i = 1; i < arr.length; i++) {if (arr[i] <= pivot) {left.push(arr[i]);} else {right.push(arr[i]);}}return [...quickSort(left), pivot, ...quickSort(right)];
}
特点:
- 时间复杂度:平均 O(n log n),最坏 O(n²)(如基准选择不当)。
- 空间复杂度:O(log n)(递归栈),非原地版本为 O(n)。
- 稳定性:不稳定。
- 优化:随机选择基准、三路快排(处理重复元素)。
5. 归并排序(Merge Sort)
核心思想:分治法,将数组分成两半,分别排序后合并。
function mergeSort(arr) {if (arr.length <= 1) return arr;const mid = Math.floor(arr.length / 2);const left = mergeSort(arr.slice(0, mid));const right = mergeSort(arr.slice(mid));return merge(left, right);
}function merge(left, right) {const result = [];let i = 0, j = 0;while (i < left.length && j < right.length) {if (left[i] <= right[j]) {result.push(left[i]);i++;} else {result.push(right[j]);j++;}}return [...result, ...left.slice(i), ...right.slice(j)];
}
特点:
- 时间复杂度:O(n log n),稳定且不受数据分布影响。
- 空间复杂度:O(n)(辅助数组)。
- 稳定性:稳定。
- 适用场景:大规模数据、外部排序。
复杂度对比表
| 算法 | 平均时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|
| 选择排序 | O(n²) | O(n²) | O(1) | 不稳定 |
| 冒泡排序 | O(n²) | O(n²) | O(1) | 稳定 |
| 插入排序 | O(n²) | O(n²) | O(1) | 稳定 |
| 快速排序 | O(n log n) | O(n²) | O(log n) | 不稳定 |
| 归并排序 | O(n log n) | O(n log n) | O(n) | 稳定 |
使用示例
const arr = [5, 3, 8, 4, 2];
console.log(selectionSort([...arr])); // [2, 3, 4, 5, 8]
console.log(bubbleSort([...arr])); // [2, 3, 4, 5, 8]
console.log(insertionSort([...arr])); // [2, 3, 4, 5, 8]
console.log(quickSort([...arr])); // [2, 3, 4, 5, 8]
console.log(mergeSort([...arr])); // [2, 3, 4, 5, 8]
注意:为避免修改原数组,传入排序函数前使用 [...arr] 复制数组。实际开发中推荐使用 JavaScript 内置的 Array.prototype.sort(),其底层基于优化的快速排序或归并排序,时间复杂度为 O(n log n)。
相关文章:

用js实现常见排序算法
以下是几种常见排序算法的 JS实现,包括选择排序、冒泡排序、插入排序、快速排序和归并排序,以及每种算法的特点和复杂度分析 1. 选择排序(Selection Sort) 核心思想:每次从未排序部分选择最小元素,与未排…...

python读取SQLite表个并生成pdf文件
代码用于创建含50列的SQLite数据库并插入500行随机浮点数据,随后读取数据,通过ReportLab生成横向PDF表格,包含格式化(两位小数)及表头、网格线等美观样式。 # 导入所需库 import sqlite3 # 用于操作…...

当下AI智能硬件方案浅谈
背景: 现在大模型出来以后,打破了常规的机械式的对话,人机对话变得更聪明一点。 对话用到的技术主要是实时音视频,简称为RTC。下游硬件厂商一般都不会去自己开发音视频技术,开发自己的大模型。商用方案多见为字节、百…...

大模型真的像人一样“思考”和“理解”吗?
Yann LeCun 新研究的核心探讨:大语言模型(LLM)的“理解”和“思考”方式与人类认知的根本差异。 核心问题:大模型真的像人一样“思考”和“理解”吗? 人类的思考方式: 你的大脑是个超级整理师。面对海量信…...

【题解-洛谷】P10480 可达性统计
题目:P10480 可达性统计 题目描述 给定一张 N N N 个点 M M M 条边的有向无环图,分别统计从每个点出发能够到达的点的数量。 输入格式 第一行两个整数 N , M N,M N,M,接下来 M M M 行每行两个整数 x , y x,y x,y,表示从 …...

在Spring Boot中集成RabbitMQ的完整指南
前言 在现代微服务架构中,消息队列(Message Queue)是实现异步通信、解耦系统组件的重要工具。RabbitMQ 是一个流行的消息中间件,支持多种消息协议,具有高可靠性和可扩展性。 本博客将详细介绍如何在 Spring Boot 项目…...
Element-Plus:popconfirm与tooltip一起使用不生效?
你们好,我是金金金。 场景 我正在使用Element-plus组件库当中的el-popconfirm和el-tooltip,产品要求是两个需要结合一起使用,也就是鼠标悬浮上去有提示文字,并且点击之后需要出现气泡确认框 代码 <el-popconfirm title"是…...

Selenium 查找页面元素的方式
Selenium 查找页面元素的方式 Selenium 提供了多种方法来查找网页中的元素,以下是主要的定位方式: 基本定位方式 通过ID定位 driver.find_element(By.ID, "element_id")通过Name定位 driver.find_element(By.NAME, "element_name"…...
OPENCV图形计算面积、弧长API讲解(1)
一.OPENCV图形面积、弧长计算的API介绍 之前我们已经把图形轮廓的检测、画框等功能讲解了一遍。那今天我们主要结合轮廓检测的API去计算图形的面积,这些面积可以是矩形、圆形等等。图形面积计算和弧长计算常用于车辆识别、桥梁识别等重要功能,常用的API…...

【Java】Ajax 技术详解
文章目录 1. Filter 过滤器1.1 Filter 概述1.2 Filter 快速入门开发步骤:1.3 Filter 执行流程1.4 Filter 拦截路径配置1.5 过滤器链2. Listener 监听器2.1 Listener 概述2.2 ServletContextListener3. Ajax 技术3.1 Ajax 概述3.2 Ajax 快速入门服务端实现:客户端实现:4. Axi…...

spring boot使用HttpServletResponse实现sse后端流式输出消息
1.以前只是看过SSE的相关文章,没有具体实践,这次接入AI大模型使用到了流式输出,涉及到给前端流式返回,所以记录一下。 2.resp要设置为text/event-stream resp.setContentType("text/event-stream"); resp.setCharacter…...

二叉树-144.二叉树的前序遍历-力扣(LeetCode)
一、题目解析 对于递归方法的前序遍历十分简单,但对于一位合格的程序猿而言,需要掌握将递归转化为非递归的能力,毕竟递归调用的时候会调用大量的栈帧,存在栈溢出风险。 二、算法原理 递归调用本质是系统建立栈帧,而非…...

无需布线的革命:电力载波技术赋能楼宇自控系统-亚川科技
无需布线的革命:电力载波技术赋能楼宇自控系统 在楼宇自动化领域,传统控制系统依赖复杂的专用通信线路,不仅施工成本高昂,后期维护和扩展也极为不便。电力载波技术(PLC)的突破性应用,彻底改变了…...

Netty自定义协议解析
目录 自定义协议设计 实现消息解码器 实现消息编码器 自定义消息对象 配置ChannelPipeline Netty提供了强大的编解码器抽象基类,这些基类能够帮助开发者快速实现自定义协议的解析。 自定义协议设计 在实现自定义协议解析之前,需要明确协议的具体格式。例如,一个简单的…...

__VUE_PROD_HYDRATION_MISMATCH_DETAILS__ is not explicitly defined.
这个警告表明您在使用Vue的esm-bundler构建版本时,未明确定义编译时特性标志。以下是详细解释和解决方案: 问题原因: 该标志是Vue 3.4引入的编译时特性标志,用于控制生产环境下SSR水合不匹配错误的详细报告1使用esm-bundler…...
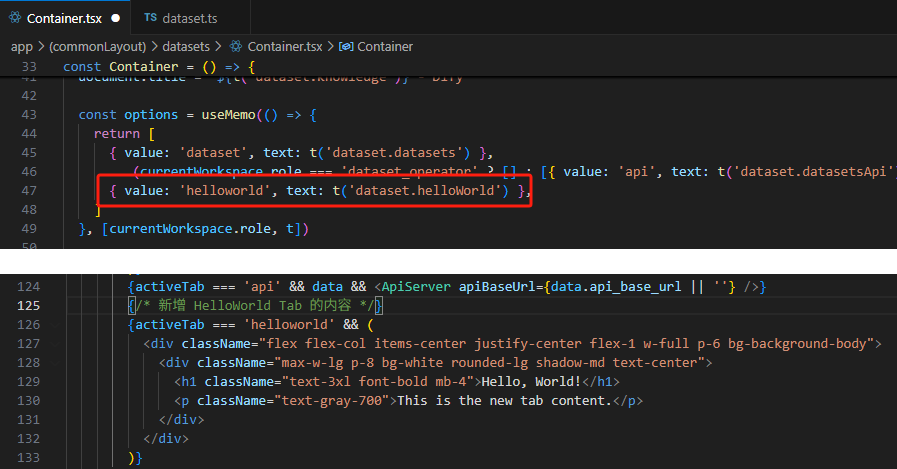
【技巧】dify前端源代码修改第一弹-增加tab页
回到目录 【技巧】dify前端源代码修改第一弹-增加tab页 尝试修改dify的前端源代码,在知识库增加一个tab页"HELLO WORLD",完成后的效果如下 [gif01] 1. 前端代码进入调试模式 参考 【部署】win10的wsl环境下启动dify的web前端服务 启动调试…...

Java设计模式:责任链模式
一、什么是责任链模式? 责任链模式(Chain of Responsibility Pattern) 是一种 行为型设计模式,它通过将请求沿着一条处理链传递,直到某个对象处理它为止。这种模式的核心思想是 解耦请求的发送者和接收者,…...

比特币:固若金汤的数字堡垒与它的四道防线
第一道防线:机密信函——无法破解的哈希加密 将每一笔比特币交易比作一封在堡垒内部传递的机密信函。 解释“哈希”(Hashing)就是一种军事级的加密术(SHA-256),能将信函内容(交易细节…...

基于 HTTP 的单向流式通信协议SSE详解
SSE(Server-Sent Events)详解 🧠 什么是 SSE? SSE(Server-Sent Events) 是 HTML5 标准中定义的一种通信机制,它允许服务器主动将事件推送给客户端(浏览器)。与传统的 H…...

初探用uniapp写微信小程序遇到的问题及解决(vue3+ts)
零、关于开发思路 (一)拿到工作任务,先理清楚需求 1.逻辑部分 不放过原型里说的每一句话,有疑惑的部分该问产品/测试/之前的开发就问 2.页面部分(含国际化) 整体看过需要开发页面的原型后,分类一下哪些组件/样式可以复用,直接提取出来使用 (时间充分的前提下,不…...

接口 RESTful 中的超媒体:REST 架构的灵魂驱动
在 RESTful 架构中,** 超媒体(Hypermedia)** 是一个核心概念,它体现了 REST 的 “表述性状态转移(Representational State Transfer)” 的本质,也是区分 “真 RESTful API” 与 “伪 RESTful AP…...

第22节 Node.js JXcore 打包
Node.js是一个开放源代码、跨平台的、用于服务器端和网络应用的运行环境。 JXcore是一个支持多线程的 Node.js 发行版本,基本不需要对你现有的代码做任何改动就可以直接线程安全地以多线程运行。 本文主要介绍JXcore的打包功能。 JXcore 安装 下载JXcore安装包&a…...

云原生时代的系统设计:架构转型的战略支点
📝个人主页🌹:一ge科研小菜鸡-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、云原生的崛起:技术趋势与现实需求的交汇 随着企业业务的互联网化、全球化、智能化持续加深,传统的 I…...

Git 命令全流程总结
以下是从初始化到版本控制、查看记录、撤回操作的 Git 命令全流程总结,按操作场景分类整理: 一、初始化与基础操作 操作命令初始化仓库git init添加所有文件到暂存区git add .提交到本地仓库git commit -m "提交描述"首次提交需配置身份git c…...
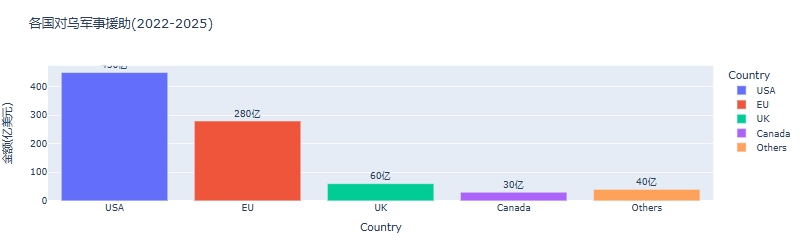
python可视化:俄乌战争时间线关键节点与深层原因
俄乌战争时间线可视化分析:关键节点与深层原因 俄乌战争是21世纪欧洲最具影响力的地缘政治冲突之一,自2022年2月爆发以来已持续超过3年。 本文将通过Python可视化工具,系统分析这场战争的时间线、关键节点及其背后的深层原因,全面…...

C# WPF 左右布局实现学习笔记(1)
开发流程视频: https://www.youtube.com/watch?vCkHyDYeImjY&ab_channelC%23DesignPro Git源码: GitHub - CSharpDesignPro/Page-Navigation-using-MVVM: WPF - Page Navigation using MVVM 1. 新建工程 新建WPF应用(.NET Framework) 2.…...

Linux入门(十五)安装java安装tomcat安装dotnet安装mysql
安装java yum install java-17-openjdk-devel查找安装地址 update-alternatives --config java设置环境变量 vi /etc/profile #在文档后面追加 JAVA_HOME"通过查找安装地址命令显示的路径" #注意一定要加$PATH不然路径就只剩下新加的路径了,系统很多命…...
【QT控件】显示类控件
目录 一、Label 二、LCD Number 三、ProgressBar 四、Calendar Widget QT专栏:QT_uyeonashi的博客-CSDN博客 一、Label QLabel 可以用来显示文本和图片. 核心属性如下 代码示例: 显示不同格式的文本 1) 在界面上创建三个 QLabel 尺寸放大一些. objectName 分别…...
)
使用python进行图像处理—图像滤波(5)
图像滤波是图像处理中最基本和最重要的操作之一。它的目的是在空间域上修改图像的像素值,以达到平滑(去噪)、锐化、边缘检测等效果。滤波通常通过卷积操作实现。 5.1卷积(Convolution)原理 卷积是滤波的核心。它是一种数学运算,…...

npm安装electron下载太慢,导致报错
npm安装electron下载太慢,导致报错 背景 想学习electron框架做个桌面应用,卡在了安装依赖(无语了)。。。一开始以为node版本或者npm版本太低问题,调整版本后还是报错。偶尔执行install命令后,可以开始下载…...
