使用python进行图像处理—图像滤波(5)
图像滤波是图像处理中最基本和最重要的操作之一。它的目的是在空间域上修改图像的像素值,以达到平滑(去噪)、锐化、边缘检测等效果。滤波通常通过卷积操作实现。
5.1卷积(Convolution)原理
卷积是滤波的核心。它是一种数学运算,将一个图像(输入信号)与一个核(Kernel或 滤波器,一个小的二维数组)进行运算,产生一个新的图像(输出信号)。
想象一个核在图像上滑动,在每一个位置,核的每个元素与图像对应位置的像素值相乘,然后将所有乘积相加,得到的和就是输出图像在该位置的像素值。
数学上,二维离散卷积可以表示为:
[
G[i, j] = \sum_m \sum_n I[i-m, j-n] K[m, n]
]
其中:
(G[i, j])是输出图像在( (i, j) )位置的像素值。
(I)是输入图像。
(K)是核(滤波器)。
(m, n)是核的索引。
在实际应用中,为了计算方便,通常使用相关的形式,但效果类似。OpenCV和scikit-image等库提供了高效的卷积实现。
5.2常见的空间滤波器
空间滤波器可以分为线性滤波器和非线性滤波器。
线性滤波器:输出像素值是输入像素值的线性组合,例如均值滤波、高斯滤波。它们可以通过卷积实现。
非线性滤波器:输出像素值不是输入像素值的线性组合,例如中值滤波。它们通常不能直接通过简单的卷积实现,但同样涉及在像素邻域内的操作。
5.2.1平滑滤波器(Smoothing Filters)
平滑滤波器用于去除图像中的噪声,模糊图像细节。它们通常是低通滤波器,衰减图像中的高频成分(如噪声和边缘)。
均值滤波器(Mean Filter):用像素邻域内的平均值替换当前像素值。
import numpy as np
from PIL import Image
# PIL 不直接提供卷积核应用函数,但我们可以用 NumPy 实现或使用其他库
# 这里我们使用 scikit-image,它提供了更方便的滤波器函数from skimage import io, filters
import matplotlib.pyplot as plt # 用于显示图像# 加载一个示例图像 (如果不存在,创建一个模拟图像)
try:img_sk = io.imread('example.jpg') # skimage io.imread 可以读取多种格式print("成功加载图像使用 skimage.io.imread")
except FileNotFoundError:print("示例图像 example.jpg 未找到,请确保文件存在。")# 如果找不到,我们创建一个模拟图像from PIL import Imageimg = Image.new('RGB', (300, 200), color = 'gray')img_sk = np.array(img) # 转换为 NumPy 数组供 skimage 使用print("已创建模拟图像数组。")# 确保图像是灰度或彩色,这里示例以灰度进行,如果加载的是彩色,先转换
if img_sk.ndim == 3:print("图像是彩色,转换为灰度进行滤波示例。")# skimage.color.rgb2gray 可以方便转换from skimage.color import rgb2grayimg_sk_gray = rgb2gray(img_sk)# rgb2gray 返回的是浮点数类型 (0.0 到 1.0),需要缩放到 0-255 并转换为 uint8 显示img_sk_gray_uint8 = (img_sk_gray * 255).astype(np.uint8)
else:img_sk_gray_uint8 = img_sk # 如果已经是灰度,直接使用# 应用均值滤波器
# 使用 skimage.filters.rank.mean
# size 参数指定邻域大小,例如 3 表示 3x3 邻域
# 这个函数需要输入是 uint8 类型
try:mean_filtered_img = filters.rank.mean(img_sk_gray_uint8, selem=np.ones((5, 5))) # 使用 5x5 的方形结构元素# 显示原始图像和均值滤波后的图像plt.figure(figsize=(10, 5))plt.subplot(1, 2, 1)plt.imshow(img_sk_gray_uint8, cmap='gray') # cmap='gray' 用于灰度图像显示plt.title('原始灰度图像')plt.axis('off') # 不显示坐标轴plt.subplot(1, 2, 2)plt.imshow(mean_filtered_img, cmap='gray')plt.title('均值滤波 (5x5)')plt.axis('off')plt.tight_layout() # 调整子图布局plt.show()# 保存结果 (使用Pillow或skimage.io.imsave)# Image.fromarray(mean_filtered_img).save('output_mean_filtered.jpg')io.imsave('output_mean_filtered_skimage.jpg', mean_filtered_img)print("均值滤波已完成并保存为: output_mean_filtered_skimage.jpg")except Exception as e:print(f"均值滤波示例执行失败: {e}")print("请检查scikit-image版本是否支持 filters.rank.mean,或尝试不同的结构元素 (selem)。")print("或者使用 scipy.ndimage.uniform_filter 进行均值滤波")# 替代方法:使用 scipy.ndimage 进行均值滤波
try:from scipy import ndimageuniform_filtered_img = ndimage.uniform_filter(img_sk_gray_uint8, size=5) # size=5 表示一个边长为5的方形核# 显示原始图像和均匀滤波后的图像plt.figure(figsize=(10, 5))plt.subplot(1, 2, 1)plt.imshow(img_sk_gray_uint8, cmap='gray')plt.title('原始灰度图像')plt.axis('off')plt.subplot(1, 2, 2)plt.imshow(uniform_filtered_img, cmap='gray')plt.title('均匀滤波 (scipy, size=5)')plt.axis('off')plt.tight_layout()plt.show()io.imsave('output_uniform_filtered_scipy.jpg', uniform_filtered_img)print("均匀滤波 (scipy) 已完成并保存为: output_uniform_filtered_scipy.jpg")except ImportError:print("未安装 scipy 库,跳过均匀滤波示例。请使用 pip install scipy 进行安装。")
except Exception as e:print(f"均匀滤波示例执行失败: {e}")代码解释:
- from skimage import io, filters:导入scikit-image库的io模块(用于读写图像)和filters模块(包含各种滤波器)。
- import matplotlib.pyplot as plt:导入Matplotlib库用于显示图像。
- img_sk = io.imread('example.jpg'):使用skimage.io.imread加载图像。scikit-image加载的图像默认是NumPy数组。
- 检查图像维度并转换为灰度:因为一些滤波函数期望灰度图像。skimage.color.rgb2gray()可以方便地将彩色图像转换为灰度图像。注意rgb2gray返回浮点数组,需要转换回uint8进行显示和一些滤波函数。
- mean_filtered_img = filters.rank.mean(img_sk_gray_uint8, selem=np.ones((5, 5))):使用skimage.filters.rank.mean()函数进行均值滤波。
- 第一个参数是输入的图像数组(需要是uint8类型)。
- selem:结构元素(structuring element),定义了邻域的形状和大小。np.ones((5, 5))创建一个5x5的全部为1的NumPy数组,表示一个5x5的方形邻域。
- plt.figure(), plt.subplot(), plt.imshow(), plt.title(), plt.axis('off'), plt.tight_layout(), plt.show():这些是Matplotlib用于创建图窗、子图,在子图中显示图像,设置标题,关闭坐标轴,调整布局并显示图像的函数。
- io.imsave('output_mean_filtered_skimage.jpg', mean_filtered_img):使用skimage.io.imsave保存滤波后的图像。
- from scipy import ndimage:导入SciPy库的ndimage模块,它也提供了图像处理函数。
- uniform_filtered_img = ndimage.uniform_filter(img_sk_gray_uint8, size=5):使用scipy.ndimage.uniform_filter()进行均匀滤波,效果等同于均值滤波。size参数指定滤波核的边长。
高斯滤波器(Gaussian Filter):使用一个高斯函数作为权重对像素邻域进行加权平均。高斯滤波器比均值滤波器引起的模糊更少,并且对抑制高斯噪声特别有效。
import numpy as np
from PIL import Image
from skimage import io, filters
import matplotlib.pyplot as plt
from scipy import ndimage # SciPy 也有高斯滤波器# 假设 img_sk_gray_uint8 是上面准备好的灰度图像 uint8 数组# 应用高斯滤波器 (使用 skimage)
# sigma 参数是高斯核的标准差,控制平滑程度,值越大越模糊
# truncate 参数控制高斯核的大小,核窗口大小通常是 (2*truncate*sigma + 1) x (2*truncate*sigma + 1)
gaussian_filtered_img_sk = filters.gaussian(img_sk_gray_uint8, sigma=2, truncate=3.5)# skimage 的 gaussian 滤波器返回浮点数数组 (0.0-1.0),需要转换回 uint8 显示和保存
gaussian_filtered_img_sk_uint8 = (gaussian_filtered_img_sk * 255).astype(np.uint8)# 应用高斯滤波器 (使用 scipy)
# sigma 参数同样是标准差
gaussian_filtered_img_sp = ndimage.gaussian_filter(img_sk_gray_uint8, sigma=2)
# scipy 的 gaussian_filter 通常返回与输入相同的 dtype,这里是 uint8# 显示原始图像和高斯滤波后的图像
plt.figure(figsize=(15, 5))plt.subplot(1, 3, 1)
plt.imshow(img_sk_gray_uint8, cmap='gray')
plt.title('原始灰度图像')
plt.axis('off')plt.subplot(1, 3, 2)
plt.imshow(gaussian_filtered_img_sk_uint8, cmap='gray')
plt.title('高斯滤波 (skimage, sigma=2)')
plt.axis('off')plt.subplot(1, 3, 3)
plt.imshow(gaussian_filtered_img_sp, cmap='gray')
plt.title('高斯滤波 (scipy, sigma=2)')
plt.axis('off')plt.tight_layout()
plt.show()# 保存结果
io.imsave('output_gaussian_filtered_skimage.jpg', gaussian_filtered_img_sk_uint8)
io.imsave('output_gaussian_filtered_scipy.jpg', gaussian_filtered_img_sp)
print("高斯滤波已完成并保存结果。")代码解释:
- gaussian_filtered_img_sk = filters.gaussian(img_sk_gray_uint8, sigma=2, truncate=3.5):使用skimage.filters.gaussian()进行高斯滤波。
- 第一个参数是输入的图像数组。
- sigma=2:设置高斯核的标准差为2。标准差越大,核越大,平滑效果越强。
- truncate=3.5:这个参数决定了高斯核的截断半径,表示高斯核将延伸到距离中心多少个标准差的位置。通常取3到4,因为高斯函数在这个范围之外的值非常小,可以忽略。
- gaussian_filtered_img_sk_uint8 = (gaussian_filtered_img_sk * 255).astype(np.uint8): skimage.filters.gaussian返回的是浮点数数组(0.0到1.0),为了显示和保存为常见的图像格式(如JPEG),需要将其乘以255并转换为uint8类型。
- gaussian_filtered_img_sp = ndimage.gaussian_filter(img_sk_gray_uint8, sigma=2):使用scipy.ndimage.gaussian_filter()进行高斯滤波。接口稍有不同,但sigma参数的含义是相同的。SciPy的函数通常会尽量保持输入的数据类型。
中值滤波器(Median Filter):用像素邻域内的中值替换当前像素值。中值滤波器是非线性滤波器,对椒盐噪声(Salt-and-pepper noise)特别有效,因为它不会引入新的极端值。
import numpy as np
from PIL import Image
from skimage import io, filters
import matplotlib.pyplot as plt
from scipy import ndimage# 假设 img_sk_gray_uint8 是上面准备好的灰度图像 uint8 数组# 为了更好地演示中值滤波,我们在图像中添加一些椒盐噪声
def add_salt_and_pepper_noise(image_array, amount=0.05):"""在图像数组中添加椒盐噪声"""img_noisy = image_array.copy()# 添加盐噪声 (白色像素)num_salt = np.ceil(amount * image_array.size * 0.5).astype(int)coords_salt = [np.random.randint(0, i - 1, num_salt) for i in image_array.shape]img_noisy[tuple(coords_salt)] = 255# 添加椒噪声 (黑色像素)num_pepper = np.ceil(amount * image_array.size * 0.5).astype(int)coords_pepper = [np.random.randint(0, i - 1, num_pepper) for i in image_array.shape]img_noisy[tuple(coords_pepper)] = 0return img_noisy# 添加噪声
img_noisy_uint8 = add_salt_and_pepper_noise(img_sk_gray_uint8, amount=0.03) # 添加3%的椒盐噪声# 应用中值滤波器 (使用 skimage)
# size 参数指定邻域大小,例如 3 表示 3x3 邻域
# skimage.filters.median 同样需要 uint8 输入
median_filtered_img_sk = filters.median(img_noisy_uint8, selem=np.ones((3, 3))) # 使用 3x3 的方形结构元素# 应用中值滤波器 (使用 scipy)
# size 参数指定邻域大小
median_filtered_img_sp = ndimage.median_filter(img_noisy_uint8, size=3)# 显示原始噪声图像和中值滤波后的图像
plt.figure(figsize=(15, 5))plt.subplot(1, 3, 1)
plt.imshow(img_noisy_uint8, cmap='gray')
plt.title('原始噪声图像')
plt.axis('off')plt.subplot(1, 3, 2)
plt.imshow(median_filtered_img_sk, cmap='gray')
plt.title('中值滤波 (skimage, size=3)')
plt.axis('off')plt.subplot(1, 3, 3)
plt.imshow(median_filtered_img_sp, cmap='gray')
plt.title('中值滤波 (scipy, size=3)')
plt.axis('off')plt.tight_layout()
plt.show()# 保存结果
io.imsave('output_median_filtered_skimage.jpg', median_filtered_img_sk)
io.imsave('output_median_filtered_scipy.jpg', median_filtered_img_sp)
print("中值滤波已完成并保存结果。")代码解释:
- def add_salt_and_pepper_noise(image_array, amount=0.05)::定义一个函数用于向图像中添加椒盐噪声,以便更好地展示中值滤波的效果。
- amount:噪声的比例,0.05表示图像总像素数的5%会变成噪声点。
- np.ceil(amount * image_array.size * 0.5).astype(int):计算需要添加的盐点和椒点的数量,假设盐点和椒点各占一半。image_array.size是图像的总像素数。
- coords_salt = [np.random.randint(0, i - 1, num_salt) for i in image_array.shape]:为盐点生成随机的行和列坐标。对于二维图像,image_array.shape是(height, width),循环会为高度和宽度生成对应的坐标数组。np.random.randint(0, i - 1, num_salt)在指定范围内生成num_salt个随机整数。
- img_noisy[tuple(coords_salt)] = 255:使用生成的随机坐标作为索引,将这些位置的像素值设置为255(白色,盐噪声)。tuple(coords_salt)是为了正确地使用NumPy的多维索引。
- 添加椒噪声的过程类似,只是像素值设置为0(黑色)。
- img_noisy_uint8 = add_salt_and_pepper_noise(img_sk_gray_uint8, amount=0.03):调用函数为灰度图像添加3%的椒盐噪声。
- median_filtered_img_sk = filters.median(img_noisy_uint8, selem=np.ones((3, 3))):使用skimage.filters.median()进行中值滤波。selem参数同样指定邻域。
- median_filtered_img_sp = ndimage.median_filter(img_noisy_uint8, size=3):使用scipy.ndimage.median_filter()进行中值滤波。size参数指定邻域大小。
5.2.2锐化滤波器(Sharpening Filters)
锐化滤波器用于增强图像的边缘和细节。它们通常是高通滤波器,增强图像中的高频成分。
拉普拉斯算子(Laplacian Operator):是一种二阶微分算子,用于检测图像中的边缘。它对噪声非常敏感。
import numpy as np
from PIL import Image
from skimage import io, filters
import matplotlib.pyplot as plt
from scipy import ndimage# 假设 img_sk_gray_uint8 是上面准备好的灰度图像 uint8 数组# 应用拉普拉斯滤波器 (使用 skimage)
# skimage.filters.laplace 返回浮点数
laplacian_filtered_img_sk = filters.laplace(img_sk_gray_uint8)# 拉普拉斯滤波器的结果通常是正负值,表示梯度的二阶变化
# 为了显示,通常取绝对值并缩放到 0-255 范围
laplacian_filtered_img_sk_abs = np.abs(laplacian_filtered_img_sk)
# 缩放到 0-255
# 找到最大值 (非零)
max_val = np.max(laplacian_filtered_img_sk_abs)
if max_val > 0:laplacian_filtered_img_sk_scaled = (laplacian_filtered_img_sk_abs / max_val * 255).astype(np.uint8)
else:laplacian_filtered_img_sk_scaled = np.zeros_like(img_sk_gray_uint8) # 如果都是零,就创建一个全黑图像# 应用拉普拉斯滤波器 (使用 scipy)
# scipy.ndimage.laplace 返回浮点数
laplacian_filtered_img_sp = ndimage.laplace(img_sk_gray_uint8)
# 同样处理结果以便显示
laplacian_filtered_img_sp_abs = np.abs(laplacian_filtered_img_sp)
max_val_sp = np.max(laplacian_filtered_img_sp_abs)
if max_val_sp > 0:laplacian_filtered_img_sp_scaled = (laplacian_filtered_img_sp_abs / max_val_sp * 255).astype(np.uint8)
else:laplacian_filtered_img_sp_scaled = np.zeros_like(img_sk_gray_uint8)# 显示原始图像和拉普拉斯滤波后的图像
plt.figure(figsize=(15, 5))plt.subplot(1, 3, 1)
plt.imshow(img_sk_gray_uint8, cmap='gray')
plt.title('原始灰度图像')
plt.axis('off')plt.subplot(1, 3, 2)
plt.imshow(laplacian_filtered_img_sk_scaled, cmap='gray')
plt.title('拉普拉斯滤波 (skimage, 缩放显示)')
plt.axis('off')plt.subplot(1, 3, 3)
plt.imshow(laplacian_filtered_img_sp_scaled, cmap='gray')
plt.title('拉普拉斯滤波 (scipy, 缩放显示)')
plt.axis('off')plt.tight_layout()
plt.show()# 保存结果
io.imsave('output_laplacian_filtered_skimage.jpg', laplacian_filtered_img_sk_scaled)
io.imsave('output_laplacian_filtered_scipy.jpg', laplacian_filtered_img_sp_scaled)
print("拉普拉斯滤波已完成并保存结果。")代码解释:
- laplacian_filtered_img_sk = filters.laplace(img_sk_gray_uint8):使用skimage.filters.laplace()应用拉普拉斯滤波器。
- laplacian_filtered_img_sk_abs = np.abs(laplacian_filtered_img_sk):计算滤波结果的绝对值。拉普拉斯算子会产生正负值,表示边缘的方向信息,但为了显示边缘强度,通常取绝对值。
- max_val = np.max(laplacian_filtered_img_sk_abs)和随后的缩放:将绝对值结果缩放到0-255范围以便以图像形式显示。这是通过将所有值除以最大值,然后乘以255实现简单的线性缩放。
- laplacian_filtered_img_sk_scaled.astype(np.uint8):将缩放后的结果转换为uint8类型。
- SciPy的ndimage.laplace()函数用法类似。
Sobel算子(Sobel Operator):是一种一阶微分算子,用于检测图像的边缘强度和方向。它包含两个卷积核,一个用于检测水平边缘(Gx),一个用于检测垂直边缘(Gy)。
- 边缘强度(Magnitude)通常计算为 ( \sqrt{G_x^2 + G_y^2} ) 或 ( |G_x| + |G_y| )。
- 边缘方向(Direction)通常计算为 ( \arctan(G_y / G_x) )。
import numpy as np
from PIL import Image
from skimage import io, filters
import matplotlib.pyplot as plt
from scipy import ndimage# 假设 img_sk_gray_uint8 是上面准备好的灰度图像 uint8 数组# 应用 Sobel 滤波器 (使用 skimage)
# filters.sobel 返回边缘强度图像 (浮点数)
sobel_filtered_img_sk = filters.sobel(img_sk_gray_uint8)# skimage.filters 还提供了单独的水平和垂直 Sobel 核应用
# sobel_horizontal = filters.sobel_h(img_sk_gray_uint8)
# sobel_vertical = filters.sobel_v(img_sk_gray_uint8)
# sobel_magnitude = np.sqrt(sobel_horizontal**2 + sobel_vertical**2) # 边缘强度# 缩放结果以便显示
# sobel 结果通常是正值,最大值可能远超255,需要缩放
sobel_filtered_img_sk_scaled = (sobel_filtered_img_sk / np.max(sobel_filtered_img_sk) * 255).astype(np.uint8)# 应用 Sobel 滤波器 (使用 scipy)
# scipy.ndimage.sobel 返回水平和垂直梯度的数组 (浮点数)
sobel_horizontal_sp = ndimage.sobel(img_sk_gray_uint8, axis=1) # axis=1 对应 x 方向 (水平边缘)
sobel_vertical_sp = ndimage.sobel(img_sk_gray_uint8, axis=0) # axis=0 对应 y 方向 (垂直边缘)# 计算边缘强度 (使用勾股定理)
sobel_magnitude_sp = np.sqrt(sobel_horizontal_sp**2 + sobel_vertical_sp**2)# 缩放结果以便显示
sobel_magnitude_sp_scaled = (sobel_magnitude_sp / np.max(sobel_magnitude_sp) * 255).astype(np.uint8)# 显示原始图像和 Sobel 滤波后的图像
plt.figure(figsize=(15, 5))plt.subplot(1, 3, 1)
plt.imshow(img_sk_gray_uint8, cmap='gray')
plt.title('原始灰度图像')
plt.axis('off')plt.subplot(1, 3, 2)
plt.imshow(sobel_filtered_img_sk_scaled, cmap='gray')
plt.title('Sobel 滤波 (skimage, 强度, 缩放显示)')
plt.axis('off')plt.subplot(1, 3, 3)
plt.imshow(sobel_magnitude_sp_scaled, cmap='gray')
plt.title('Sobel 滤波 (scipy, 强度, 缩放显示)')
plt.axis('off')plt.tight_layout()
plt.show()# 保存结果
io.imsave('output_sobel_filtered_skimage.jpg', sobel_filtered_img_sk_scaled)
io.imsave('output_sobel_filtered_scipy.jpg', sobel_magnitude_sp_scaled)
print("Sobel 滤波已完成并保存结果。")代码解释:
- sobel_filtered_img_sk = filters.sobel(img_sk_gray_uint8):使用skimage.filters.sobel()计算图像的Sobel边缘强度。它内部计算了水平和垂直梯度,然后结合起来得到边缘强度。返回浮点数数组。
- sobel_filtered_img_sk_scaled = (sobel_filtered_img_sk / np.max(sobel_filtered_img_sk) * 255).astype(np.uint8):对Sobel结果进行缩放以便显示。Sobel结果通常是正值,最大值可能很大,需要除以最大值进行归一化(缩放到0-1范围),然后乘以255转换为0-255范围的uint8。
- sobel_horizontal_sp = ndimage.sobel(img_sk_gray_uint8, axis=1)和sobel_vertical_sp = ndimage.sobel(img_sk_gray_uint8, axis=0):使用scipy.ndimage.sobel()分别计算水平(axis=1)和垂直(axis=0)方向的Sobel梯度。返回浮点数数组,可能包含负值。
- sobel_magnitude_sp = np.sqrt(sobel_horizontal_sp2 + sobel_vertical_sp2):根据水平和垂直梯度计算边缘强度,这里使用了欧几里得距离(勾股定理)。
- sobel_magnitude_sp_scaled = (sobel_magnitude_sp / np.max(sobel_magnitude_sp) * 255).astype(np.uint8):对SciPy计算的边缘强度进行缩放以便显示。
还有许多其他的滤波器,例如Prewitt算子、Roberts算子、Canny边缘检测器(通常认为是边缘检测算法而不是简单的滤波器,但涉及滤波步骤)。
5.3卷积核的创建与应用(手动)
虽然库函数很方便,但理解如何手动应用卷积核有助于深入理解滤波原理。我们可以创建一个自定义的卷积核,然后使用SciPy的convolve或convolve2d函数应用它。
import numpy as np
from PIL import Image
from skimage import io
from scipy.ndimage import convolve, convolve1d # convolve for multi-dim, convolve1d for 1D
import matplotlib.pyplot as plt# 假设 img_sk_gray_uint8 是上面准备好的灰度图像 uint8 数组
# 转换为浮点数进行卷积,因为卷积结果可能有小数或超出 0-255 范围
img_float = img_sk_gray_uint8.astype(np.float64) # 使用 float64 确保精度# 创建一个 3x3 的均值滤波核
mean_kernel = np.ones((3, 3)) / 9.0
print("3x3 均值滤波核:\n", mean_kernel)# 创建一个 3x3 的高斯近似核 (简单的示例,不是精确的高斯核)
# weights = [1, 2, 1] for 1D, [1, 2, 1]x[1, 2, 1] for 2D (Outer product)
gaussian_approx_kernel = np.array([[1, 2, 1],[2, 4, 2],[1, 2, 1]], dtype=np.float64) / 16.0
print("3x3 高斯近似核:\n", gaussian_approx_kernel)# 创建一个 3x3 的锐化核 (中心增强,周围抑制)
# 这是一个简单的锐化核,可以增强边缘
sharpen_kernel = np.array([[ 0, -1, 0],[-1, 5, -1],[ 0, -1, 0]], dtype=np.float64)
print("3x3 锐化核:\n", sharpen_kernel)# 创建一个 3x3 的边缘检测核 (示例:简单的差分核)
edge_kernel = np.array([[ 0, -1, 0],[-1, 4, -1],[ 0, -1, 0]], dtype=np.float64) # 类似于拉普拉斯核
print("3x3 边缘检测核 (拉普拉斯近似):\n", edge_kernel)# 应用卷积核
# SciPy 的 convolve 函数
# input: 输入数组
# weights: 卷积核
# mode: 边界处理方式 ('constant', 'nearest', 'reflect', 'wrap')
# 'constant': 填充常数 (cval 参数指定),默认0
# 'nearest': 边界像素值延伸
# 'reflect': 反射边界
# 'wrap': 环绕边界
# cval: constant 模式下的填充值
# origin: 核的中心点偏移 (通常为 0 表示中心)# 应用均值滤波核
mean_convolved_img = convolve(img_float, mean_kernel, mode='nearest')# 应用高斯近似核
gaussian_convolved_img = convolve(img_float, gaussian_approx_kernel, mode='nearest')# 应用锐化核
sharpen_convolved_img = convolve(img_float, sharpen_kernel, mode='nearest')# 应用边缘检测核
edge_convolved_img = convolve(img_float, edge_kernel, mode='nearest')# 将结果转换回 uint8 进行显示和保存
# 卷积结果可能超出 0-255 范围,需要裁剪和转换
mean_convolved_img_uint8 = np.clip(mean_convolved_img, 0, 255).astype(np.uint8)
gaussian_convolved_img_uint8 = np.clip(gaussian_convolved_img, 0, 255).astype(np.uint8)
sharpen_convolved_img_uint8 = np.clip(sharpen_convolved_img, 0, 255).astype(np.uint8)
edge_convolved_img_uint8 = np.clip(edge_convolved_img, 0, 255).astype(np.uint8)# 显示结果
plt.figure(figsize=(20, 10))plt.subplot(2, 3, 1)
plt.imshow(img_sk_gray_uint8, cmap='gray')
plt.title('原始灰度图像')
plt.axis('off')plt.subplot(2, 3, 2)
plt.imshow(mean_convolved_img_uint8, cmap='gray')
plt.title('均值卷积 (3x3)')
plt.axis('off')plt.subplot(2, 3, 3)
plt.imshow(gaussian_convolved_img_uint8, cmap='gray')
plt.title('高斯近似卷积 (3x3)')
plt.axis('off')plt.subplot(2, 3, 4)
plt.imshow(sharpen_convolved_img_uint8, cmap='gray')
plt.title('锐化卷积 (3x3)')
plt.axis('off')plt.subplot(2, 3, 5)
plt.imshow(edge_convolved_img_uint8, cmap='gray')
plt.title('边缘检测卷积 (3x3)')
plt.axis('off')plt.tight_layout()
plt.show()# 保存结果
io.imsave('output_mean_convolved.jpg', mean_convolved_img_uint8)
io.imsave('output_gaussian_convolved.jpg', gaussian_convolved_img_uint8)
io.imsave('output_sharpen_convolved.jpg', sharpen_convolved_img_uint8)
io.imsave('output_edge_convolved.jpg', edge_convolved_img_uint8)
print("手动卷积已完成并保存结果。")代码解释:
- from scipy.ndimage import convolve:导入SciPy的convolve函数,用于多维卷积。
- img_float = img_sk_gray_uint8.astype(np.float64):将图像数据转换为浮点数类型。这是进行卷积的标准做法,因为卷积涉及乘积求和,结果可能有小数或超出uint8的范围。使用float64提供更高的精度。
- mean_kernel = np.ones((3, 3)) / 9.0:创建一个3x3的均值滤波核。所有元素都是1,然后除以总元素个数(9),使核的总和为1,这样在平坦区域卷积后亮度不会改变。
- gaussian_approx_kernel = np.array([...]) / 16.0:创建一个3x3的高斯近似核。这个核的权重是根据二维离散高斯函数的形状设计的,中心权重最高,向外递减。核的总和为16,除以16进行归一化。
- sharpen_kernel = np.array([...]):创建一个锐化核。这个核的设计原理是:中心像素减去其邻域像素的加权和(例如,中心权重为5,四个邻居权重为-1)。这会突出中心像素相对于其周围的变化,从而增强边缘。
- edge_kernel = np.array([...]):创建一个边缘检测核,这里是一个简单的拉普拉斯核近似。中心权重为正,周围权重为负,总和为0。它检测像素值变化的“凸起”或“凹陷”,对应于边缘。
- convolve(img_float, mean_kernel, mode='nearest'):使用scipy.ndimage.convolve()函数应用卷积核。
- 第一个参数是输入图像数组(浮点数类型)。
- 第二个参数是卷积核数组。
- mode='nearest':指定边界处理方式。'nearest'模式表示在图像边界之外的区域,用最近的边界像素值进行填充。其他模式如'constant' (用常数填充,默认0)、'reflect' (反射边界)和'wrap' (环绕边界)适用于不同场景。边界处理会影响滤波结果在图像边缘的表现。
- np.clip(..., 0, 255).astype(np.uint8):将卷积结果裁剪到0-255范围并转换回uint8类型,以便显示和保存为标准图像格式。锐化和边缘检测的结果可能包含负值或超出255的值,裁剪是必须的。
手动创建和应用卷积核,可以帮助我们理解各种滤波效果是如何通过不同的权重组合实现的。
5.4频域滤波简介(使用傅里叶变换)
除了在空间域进行滤波,图像处理也可以在频域进行。通过傅里叶变换,可以将图像从空间域转换到频域,表示图像中不同频率成分的强度。在频域中,高频成分对应于图像的细节、噪声和边缘,低频成分对应于图像的平滑区域和整体结构。
频域滤波的步骤:
- 对图像进行傅里叶变换。
- 在频域中设计一个滤波器(一个与频域图像相同大小的掩模),根据需要抑制或增强特定频率成分。
- 将频域图像与滤波器相乘(逐元素相乘)。
- 对结果进行逆傅里叶变换,将图像转换回空间域。
import numpy as np
from PIL import Image
from skimage import io, color
from scipy.fft import fft2, ifft2, fftshift, ifftshift # 导入二维傅里叶变换相关函数
import matplotlib.pyplot as plt# 假设 img_sk_gray_uint8 是上面准备好的灰度图像 uint8 数组# 转换为浮点数类型进行傅里叶变换
img_float = img_sk_gray_uint8.astype(np.float64)# 1. 进行二维傅里叶变换 (FFT)
# fft2() 计算二维快速傅里叶变换
# 结果是复数数组
f_transform = fft2(img_float)# 2. 将零频率成分(直流成分)移到频谱中心
# fftshift() 将零频率分量移动到频谱中心,便于可视化和频域滤波核的设计
f_transform_shifted = fftshift(f_transform)# 可视化频谱 (幅度谱)
# 幅度谱表示不同频率成分的强度
# np.abs() 计算复数的幅度
# np.log() 用于压缩幅度范围,因为直流成分的幅度通常远大于其他频率成分
magnitude_spectrum = np.log(np.abs(f_transform_shifted) + 1) # 加1避免log(0)# 显示原始图像和幅度谱
plt.figure(figsize=(12, 6))plt.subplot(1, 2, 1)
plt.imshow(img_sk_gray_uint8, cmap='gray')
plt.title('原始灰度图像')
plt.axis('off')plt.subplot(1, 2, 2)
plt.imshow(magnitude_spectrum, cmap='gray')
plt.title('幅度谱 (对数缩放)')
plt.axis('off')plt.tight_layout()
plt.show()# 3. 设计频域滤波器 (例如,一个简单的低通滤波器)
# 低通滤波器保留低频成分,抑制高频成分,用于平滑图像
# 我们创建一个中心是1(保留低频),边缘是0(抑制高频)的掩模rows, cols = img_float.shape
center_row, center_col = rows // 2, cols // 2# 创建一个与频域图像相同尺寸的掩模
low_pass_filter = np.zeros((rows, cols), dtype=np.float64)# 定义截止频率 (距离中心多远算低频)
cutoff_radius = 30 # 像素单位的距离# 在掩模中,距离中心小于截止频率的区域设置为1
# 使用 NumPy 的广播和距离计算
y, x = np.ogrid[:rows, :cols]
distance_from_center = np.sqrt((x - center_col)**2 + (y - center_row)**2)
low_pass_filter[distance_from_center <= cutoff_radius] = 1.0# 注意:这个简单的低通滤波器是一个理想低通滤波器,在截止频率处突变,可能会引入振铃效应
# 实际应用中常使用 Butterworth 或 Gaussian 低通滤波器,它们过渡更平滑# 4. 在频域中应用滤波器 (逐元素相乘)
# 将移频后的频谱与滤波器掩模相乘
filtered_f_transform_shifted = f_transform_shifted * low_pass_filter# 5. 将零频率成分移回左上角
# ifftshift() 将零频率分量移回原始位置
filtered_f_transform = ifftshift(filtered_f_transform_shifted)# 6. 进行二维逆傅里叶变换 (IFFT)
# ifft2() 计算二维逆快速傅里叶变换
# 结果是复数,但对于实数图像,其逆变换的实部就是滤波后的图像
filtered_img_float = ifft2(filtered_f_transform).real# 裁剪并转换回 uint8 进行显示和保存
filtered_img_uint8 = np.clip(filtered_img_float, 0, 255).astype(np.uint8)# 显示原始图像和频域低通滤波后的图像
plt.figure(figsize=(12, 6))plt.subplot(1, 2, 1)
plt.imshow(img_sk_gray_uint8, cmap='gray')
plt.title('原始灰度图像')
plt.axis('off')plt.subplot(1, 2, 2)
plt.imshow(filtered_img_uint8, cmap='gray')
plt.title('频域低通滤波 (截止频率=30)')
plt.axis('off')plt.tight_layout()
plt.show()# 保存结果
io.imsave('output_frequency_lowpass_filtered.jpg', filtered_img_uint8)
print("频域低通滤波已完成并保存结果。")# 设计一个高通滤波器
# 高通滤波器保留高频成分,抑制低频成分,用于边缘检测或锐化
# 高通滤波器 = 1 - 低通滤波器 (对于理想滤波器)
high_pass_filter = 1.0 - low_pass_filter# 在频域中应用高通滤波器
filtered_f_transform_shifted_hp = f_transform_shifted * high_pass_filter# 逆移频
filtered_f_transform_hp = ifftshift(filtered_f_transform_shifted_hp)# 逆傅里叶变换
filtered_img_float_hp = ifft2(filtered_f_transform_hp).real# 裁剪并转换回 uint8
filtered_img_uint8_hp = np.clip(filtered_img_float_hp, 0, 255).astype(np.uint8)# 显示原始图像和频域高通滤波后的图像
plt.figure(figsize=(12, 6))plt.subplot(1, 2, 1)
plt.imshow(img_sk_gray_uint8, cmap='gray')
plt.title('原始灰度图像')
plt.axis('off')plt.subplot(1, 2, 2)
plt.imshow(filtered_img_uint8_hp, cmap='gray')
plt.title('频域高通滤波 (截止频率=30)')
plt.axis('off')plt.tight_layout()
plt.show()# 保存结果
io.imsave('output_frequency_highpass_filtered.jpg', filtered_img_uint8_hp)
print("频域高通滤波已完成并保存结果。")代码解释:
- from scipy.fft import fft2, ifft2, fftshift, ifftshift:导入SciPy库中用于二维傅里叶变换和逆变换以及频谱移位的函数。
- img_float = img_sk_gray_uint8.astype(np.float64):将图像数据转换为浮点数类型。进行傅里叶变换通常需要浮点数输入,因为结果是复数。
- f_transform = fft2(img_float):对图像数组进行二维快速傅里叶变换。结果f_transform是一个与输入图像同尺寸的复数NumPy数组。
- f_transform_shifted = fftshift(f_transform):使用fftshift()将频谱的零频率成分(DC分量,代表图像的平均亮度)从左上角移动到频谱的中心。这使得低频成分集中在中心,高频成分分布在边缘,更便于设计频域滤波器和可视化频谱。
- magnitude_spectrum = np.log(np.abs(f_transform_shifted) + 1):计算并可视化幅度谱。np.abs()计算复数数组的幅度(强度)。np.log(... + 1)用于对幅度进行对数缩放,因为直流成分的幅度通常比其他频率成分大很多,对数缩放可以使其他部分的细节更清晰可见。加1是为了避免log(0)。
- low_pass_filter = np.zeros((rows, cols), dtype=np.float64):创建一个与频域图像(频谱)同尺寸的NumPy数组,用于作为频域低通滤波器掩模。初始化为零。
- center_row, center_col = rows // 2, cols // 2:计算频谱的中心坐标。
- y, x = np.ogrid[:rows, :cols]:创建网格坐标数组,用于计算每个点到中心的距离。
- distance_from_center = np.sqrt((x - center_col)**2 + (y - center_row)**2):计算每个频域点到中心的欧几里得距离。在频域中,距离中心越近代表频率越低,距离越远代表频率越高。
- low_pass_filter[distance_from_center <= cutoff_radius] = 1.0:设计一个理想低通滤波器。在距离中心小于等于cutoff_radius的区域,将掩模值设置为1.0(允许这些频率通过);在其他区域(高频),掩模值保持为0(阻止这些频率通过)。
- filtered_f_transform_shifted = f_transform_shifted * low_pass_filter:在频域中应用滤波器。将移频后的频谱与滤波器掩模进行逐元素乘法。
- filtered_f_transform = ifftshift(filtered_f_transform_shifted):使用ifftshift()将零频率成分移回原始位置(左上角),为逆傅里叶变换做准备。
- filtered_img_float = ifft2(filtered_f_transform).real:对滤波后的频域图像进行二维逆快速傅里叶变换。结果ifft2()返回复数,但对于从实数图像变换来的频谱,其逆变换的虚部理论上应该非常接近于零(由于浮点误差可能有微小非零值),因此取实部.real就是滤波后的空间域图像。
- filtered_img_uint8 = np.clip(filtered_img_float, 0, 255).astype(np.uint8):将逆变换结果裁剪到0-255范围并转换为uint8类型,以便显示和保存。
- high_pass_filter = 1.0 - low_pass_filter:设计一个理想高通滤波器。对于理想滤波器,高通滤波器掩模可以通过将低通滤波器掩模的值取反(1减去原值)得到。高通滤波器保留高频成分,抑制低频成分。
- 频域高通滤波的过程与低通滤波类似,只是使用了不同的滤波器掩模。
频域滤波提供了另一种强大的视角来理解和操作图像。通过在频域中选择性地处理不同频率成分,我们可以实现空间域中难以或效率低下的滤波效果。
相关文章:
)
使用python进行图像处理—图像滤波(5)
图像滤波是图像处理中最基本和最重要的操作之一。它的目的是在空间域上修改图像的像素值,以达到平滑(去噪)、锐化、边缘检测等效果。滤波通常通过卷积操作实现。 5.1卷积(Convolution)原理 卷积是滤波的核心。它是一种数学运算,…...

npm安装electron下载太慢,导致报错
npm安装electron下载太慢,导致报错 背景 想学习electron框架做个桌面应用,卡在了安装依赖(无语了)。。。一开始以为node版本或者npm版本太低问题,调整版本后还是报错。偶尔执行install命令后,可以开始下载…...

职坐标物联网全栈开发全流程解析
物联网全栈开发涵盖从物理设备到上层应用的完整技术链路,其核心流程可归纳为四大模块:感知层数据采集、网络层协议交互、平台层资源管理及应用层功能实现。每个模块的技术选型与实现方式直接影响系统性能与扩展性,例如传感器选型需平衡精度与…...

6.9本日总结
一、英语 复习默写list11list18,订正07年第3篇阅读 二、数学 学习线代第一讲,写15讲课后题 三、408 学习计组第二章,写计组习题 四、总结 明天结束线代第一章和计组第二章 五、明日计划 英语:复习l默写sit12list17&#…...

RLHF vs RLVR:对齐学习中的两种强化方式详解
在语言模型对齐(alignment)中,强化学习(RL)是一种重要的策略。而其中两种典型形式——RLHF(Reinforcement Learning with Human Feedback) 与 RLVR(Reinforcement Learning with Ver…...

OpenGL-什么是软OpenGL/软渲染/软光栅?
软OpenGL(Software OpenGL)或者软渲染指完全通过CPU模拟实现的OpenGL渲染方式(包括几何处理、光栅化、着色等),不依赖GPU硬件加速。这种模式通常性能较低,但兼容性极强,常用于不支持硬件加速…...
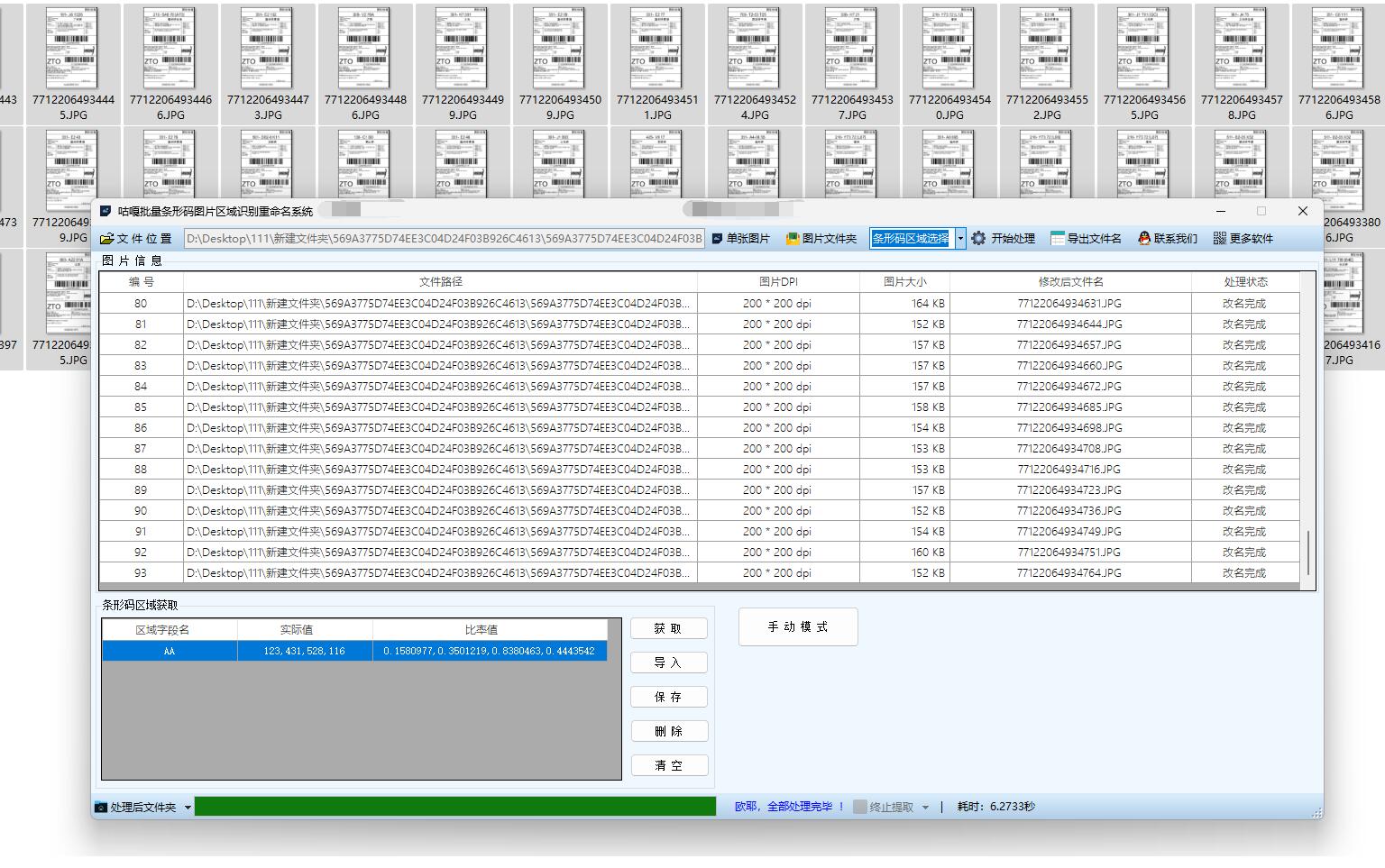
【工具教程】多个条形码识别用条码内容对图片重命名,批量PDF条形码识别后用条码内容批量改名,使用教程及注意事项
一、条形码识别改名使用教程 打开软件并选择处理模式:打开软件后,根据要处理的文件类型,选择 “图片识别模式” 或 “PDF 识别模式”。如果是处理包含条形码的 PDF 文件,就选择 “PDF 识别模式”;若是处理图片文件&…...

英国云服务器上安装宝塔面板(BT Panel)
在英国云服务器上安装宝塔面板(BT Panel) 是完全可行的,尤其适合需要远程管理Linux服务器、快速部署网站、数据库、FTP、SSL证书等服务的用户。宝塔面板以其可视化操作界面和强大的功能广受国内用户欢迎,虽然官方主要面向中国大陆…...
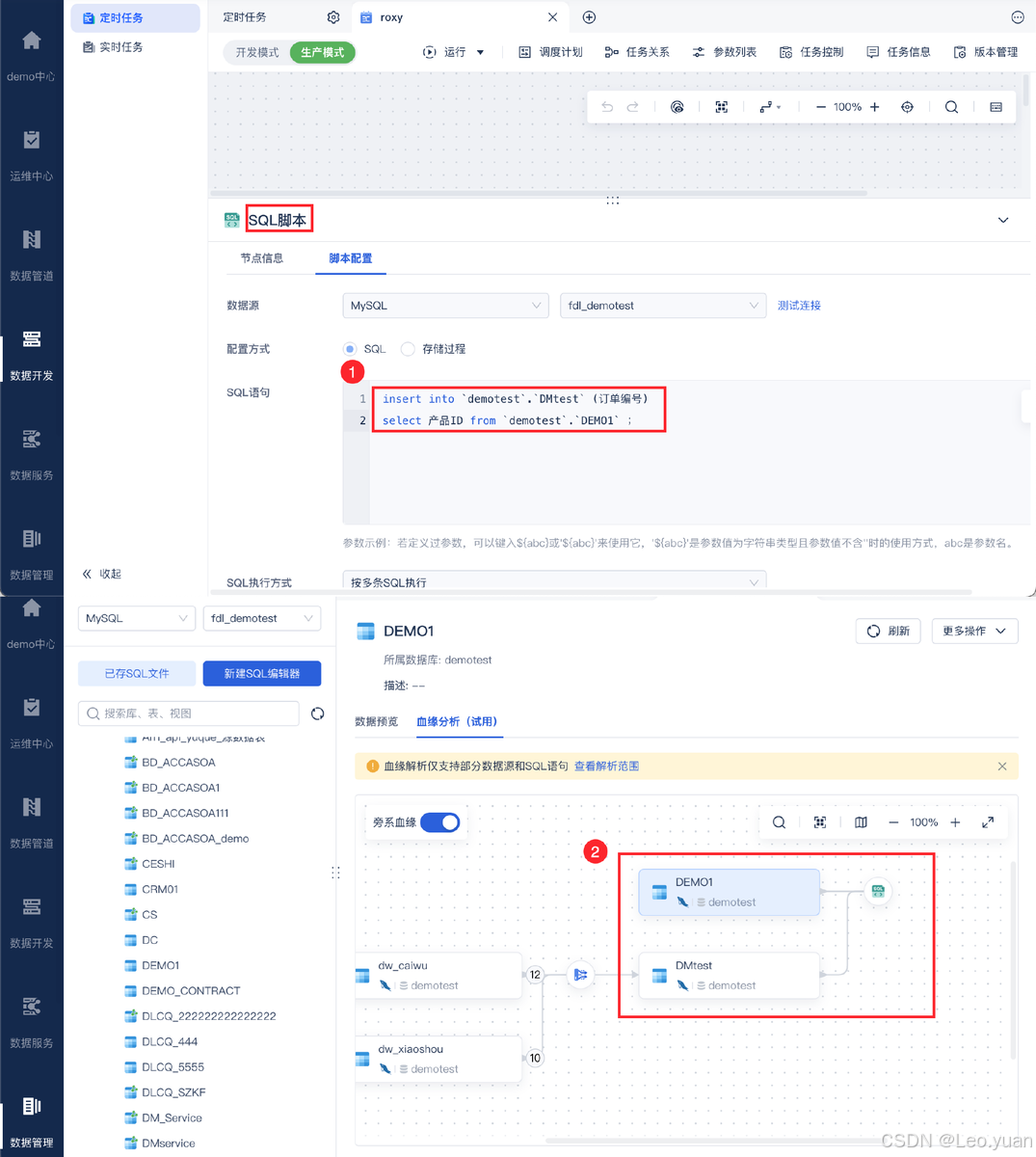
数据挖掘是什么?数据挖掘技术有哪些?
目录 一、数据挖掘是什么 二、常见的数据挖掘技术 1. 关联规则挖掘 2. 分类算法 3. 聚类分析 4. 回归分析 三、数据挖掘的应用领域 1. 商业领域 2. 医疗领域 3. 金融领域 4. 其他领域 四、数据挖掘面临的挑战和未来趋势 1. 面临的挑战 2. 未来趋势 五、总结 数据…...

Cursor AI 账号纯净度维护与高效注册指南
Cursor AI 账号纯净度维护与高效注册指南:解决限制问题的实战方案 风车无限免费邮箱系统网页端使用说明|快速获取邮箱|cursor|windsurf|augment 问题背景 在成功解决 Cursor 环境配置问题后,许多开发者仍面临账号纯净度不足导致的限制问题。无论使用 16…...

用 FFmpeg 实现 RTMP 推流直播
RTMP(Real-Time Messaging Protocol) 是直播行业中常用的传输协议。 一般来说,直播服务商会给你: ✅ 一个 RTMP 推流地址(你推视频上去) ✅ 一个 HLS 或 FLV 拉流地址(观众观看用)…...

简约商务通用宣传年终总结12套PPT模版分享
IOS风格企业宣传PPT模版,年终工作总结PPT模版,简约精致扁平化商务通用动画PPT模版,素雅商务PPT模版 简约商务通用宣传年终总结12套PPT模版分享:商务通用年终总结类PPT模版https://pan.quark.cn/s/ece1e252d7df...

P10909 [蓝桥杯 2024 国 B] 立定跳远
# P10909 [蓝桥杯 2024 国 B] 立定跳远 ## 题目描述 在运动会上,小明从数轴的原点开始向正方向立定跳远。项目设置了 $n$ 个检查点 $a_1, a_2, \cdots , a_n$ 且 $a_i \ge a_{i−1} > 0$。小明必须先后跳跃到每个检查点上且只能跳跃到检查点上。同时࿰…...

【Qt】控件 QWidget
控件 QWidget 一. 控件概述二. QWidget 的核心属性可用状态:enabled几何:geometrywindows frame 窗口框架的影响 窗口标题:windowTitle窗口图标:windowIconqrc 机制 窗口不透明度:windowOpacity光标:cursor…...
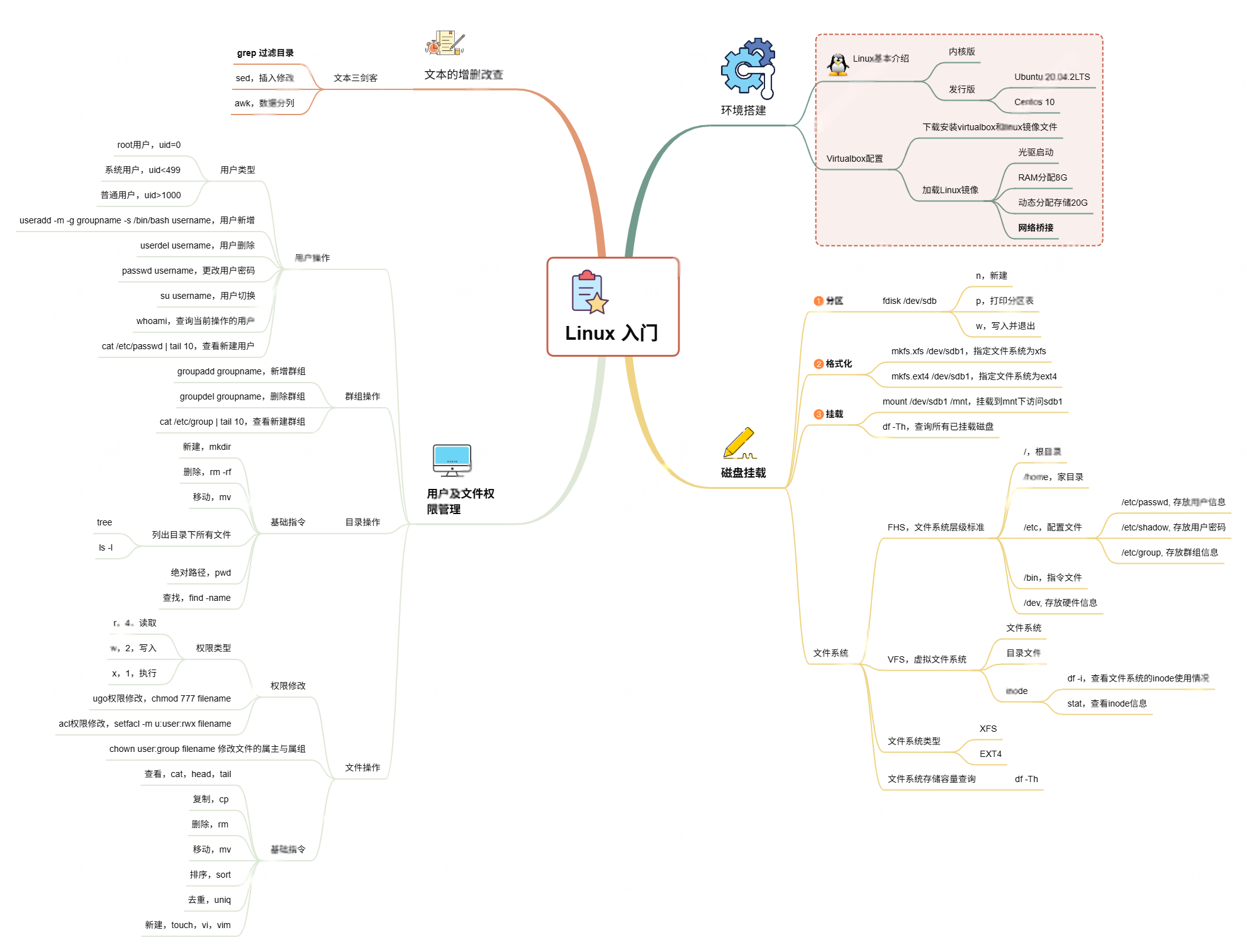
Linux入门课的思维导图
耗时两周,终于把慕课网上的Linux的基础入门课实操、总结完了! 第一次以Blog的形式做学习记录,过程很有意思,但也很耗时。 课程时长5h,涉及到很多专有名词,要去逐个查找,以前接触过的概念因为时…...

aurora与pcie的数据高速传输
设备:zynq7100; 开发环境:window; vivado版本:2021.1; 引言 之前在前面两章已经介绍了aurora读写DDR,xdma读写ddr实验。这次我们做一个大工程,pc通过pcie传输给fpga,fpga再通过aur…...

Springboot 高校报修与互助平台小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,高校报修与互助平台小程序被用户普遍使用,为…...

Linux 内存管理调试分析:ftrace、perf、crash 的系统化使用
Linux 内存管理调试分析:ftrace、perf、crash 的系统化使用 Linux 内核内存管理是构成整个内核性能和系统稳定性的基础,但这一子系统结构复杂,常常有设置失败、性能展示不良、OOM 杀进程等问题。要分析这些问题,需要一套工具化、…...

MLP实战二:MLP 实现图像数字多分类
任务 实战(二):MLP 实现图像多分类 基于 mnist 数据集,建立 mlp 模型,实现 0-9 数字的十分类 task: 1、实现 mnist 数据载入,可视化图形数字; 2、完成数据预处理:图像数据维度转换与…...

【汇编逆向系列】六、函数调用包含多个参数之多个整型-参数压栈顺序,rcx,rdx,r8,r9寄存器
从本章节开始,进入到函数有多个参数的情况,前面几个章节中介绍了整型和浮点型使用了不同的寄存器在进行函数传参,ECX是整型的第一个参数的寄存器,那么多个参数的情况下函数如何传参,下面展开介绍参数为整型时候的几种情…...

C#最佳实践:为何优先使用as或is而非强制转换
C#最佳实践:为何优先使用as或is而非强制转换 在 C# 的编程世界里,类型转换是我们经常会遇到的操作。就像在现实生活中,我们可能需要把不同形状的物品重新整理归类一样,在代码里,我们也常常需要将一个数据类型转换为另…...
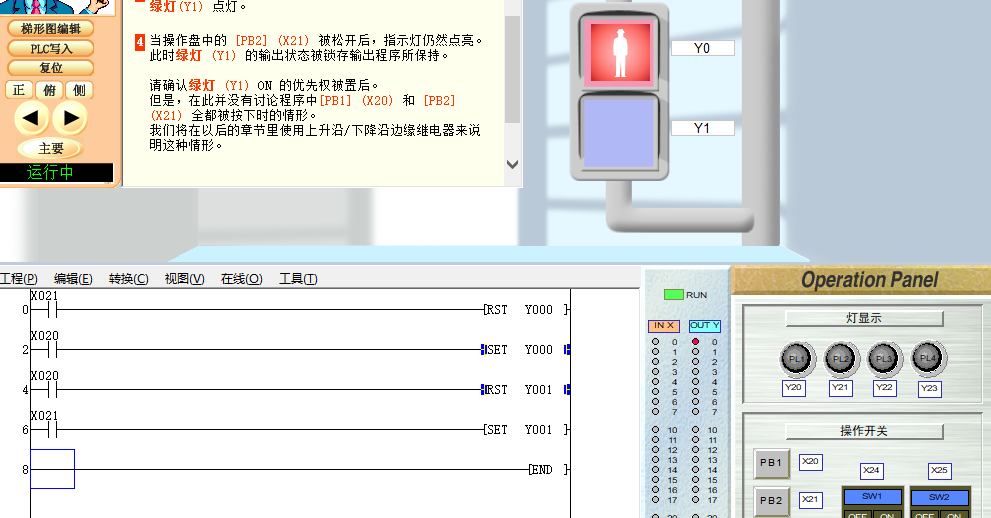
PLC入门【4】基本指令2(SET RST)
04 基本指令2 PLC编程第四课基本指令(2) 1、运用上接课所学的基本指令完成个简单的实例编程。 2、学习SET--置位指令 3、RST--复位指令 打开软件(FX-TRN-BEG-C),从 文件 - 主画面,“B: 让我们学习基本的”- “B-3.控制优先程序”。 点击“梯形图编辑”…...
react更新页面数据,操作页面,双向数据绑定
// 路由不是组件的直接跳转use client,useEffect,useRouter,需3个结合, use client表示客户端 use client; import { Button,Card, Space,Tag,Table,message,Input } from antd; import { useEffect,useState } from react; impor…...

PostgreSQL 与 SQL 基础:为 Fast API 打下数据基础
在构建任何动态、数据驱动的Web API时,一个稳定高效的数据存储方案是不可或缺的。对于使用Python FastAPI的开发者来说,深入理解关系型数据库的工作原理、掌握SQL这门与数据库“对话”的语言,以及学会如何在Python中操作数据库,是…...

Python异步编程:深入理解协程的原理与实践指南
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 持续学习,不断…...

Ray框架:分布式AI训练与调参实践
Ray框架:分布式AI训练与调参实践 系统化学习人工智能网站(收藏):https://www.captainbed.cn/flu 文章目录 Ray框架:分布式AI训练与调参实践摘要引言框架架构解析1. 核心组件设计2. 关键技术实现2.1 动态资源调度2.2 …...

基于小程序老人监护管理系统源码数据库文档
摘 要 近年来,随着我国人口老龄化问题日益严重,独居和居住养老机构的的老年人数量越来越多。而随着老年人数量的逐步增长,随之而来的是日益突出的老年人问题,尤其是老年人的健康问题,尤其是老年人产生健康问题后&…...

el-amap-bezier-curve运用及线弧度设置
文章目录 简介示例线弧度属性主要弧度相关属性其他相关样式属性完整示例链接简介 el-amap-bezier-curve 是 Vue-Amap 组件库中的一个组件,用于在 高德地图 上绘制贝塞尔曲线。 基本用法属性path定义曲线的路径,可以是多个弧线段的组合。stroke-weight线条的宽度。stroke…...

深入浅出JavaScript中的ArrayBuffer:二进制数据的“瑞士军刀”
深入浅出JavaScript中的ArrayBuffer:二进制数据的“瑞士军刀” 在JavaScript中,我们经常需要处理文本、数组、对象等数据类型。但当我们需要处理文件上传、图像处理、网络通信等场景时,单纯依赖字符串或数组就显得力不从心了。这时ÿ…...
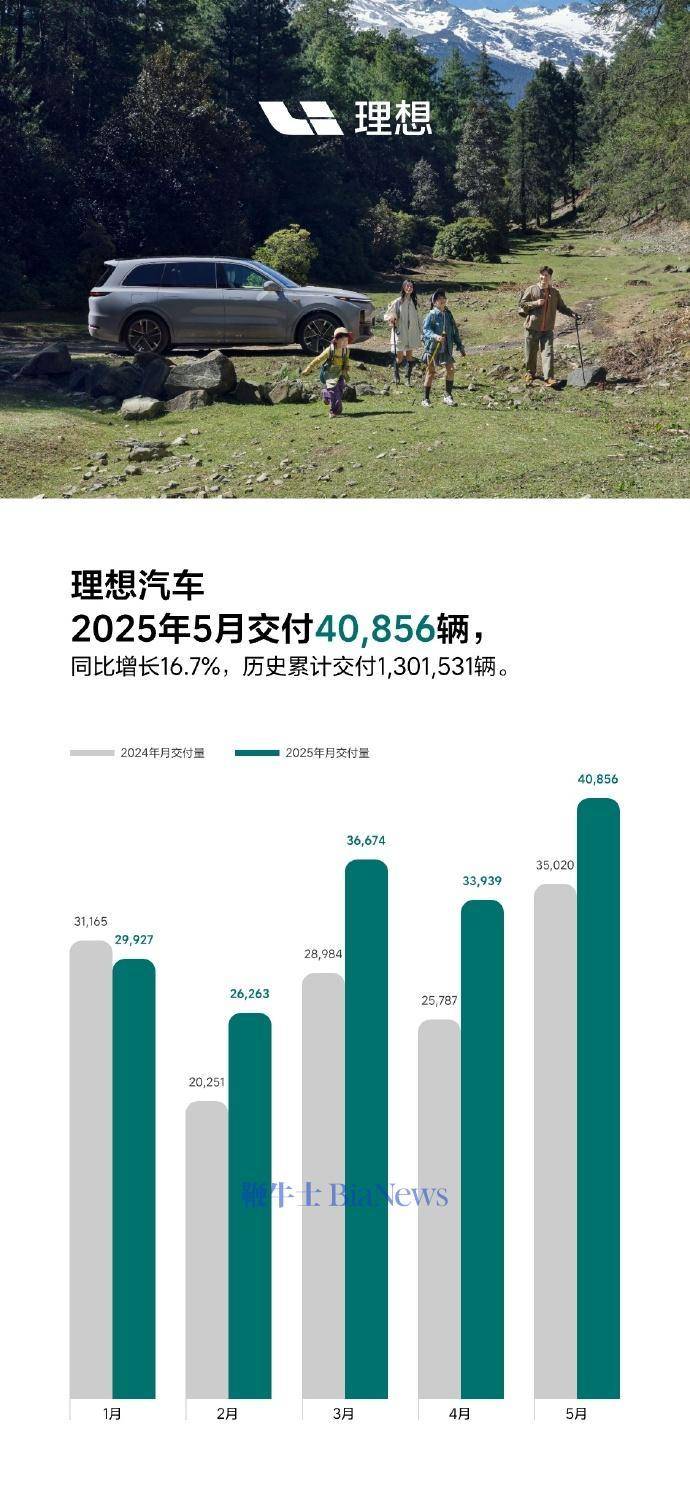
理想汽车5月交付40856辆,同比增长16.7%
6月1日,理想汽车官方宣布,5月交付新车40856辆,同比增长16.7%。截至2025年5月31日,理想汽车历史累计交付量为1301531辆。 官方表示,理想L系列智能焕新版在5月正式发布,全系产品力有显著的提升,每…...
