统计学(第8版)——统计抽样学习笔记(考试用)
一、统计抽样的核心内容与问题
研究内容
- 从总体中科学抽取样本的方法
- 利用样本数据推断总体特征(均值、比率、总量)
- 控制抽样误差与非抽样误差
解决的核心问题
- 在成本约束下,用少量样本准确推断总体特征
- 量化估计结果的可靠性(置信区间)
二、基本概念(7.1节)
| 术语 | 定义 |
|---|---|
| 总体 | 研究对象的全体 |
| 样本 | 从总体中抽取的部分元素集合 |
| 目标总体 | 待推断的总体(理论范围) |
| 抽样总体 | 实际抽取样本的总体(操作范围) |
| 抽样单位 | 抽样的基本单元(个体或一组个体) |
| 抽样框 | 抽样单位的名册清单 |
关键提示:抽样框必须完整覆盖抽样总体,否则会引入覆盖误差
三、抽样调查方法与误差(7.2-7.3节)
调查方法
- 邮寄调查
- 电话调查
- 个人采访调查
误差分类
- 非抽样误差
- 测量误差
- 采访者误差
- 数据处理误差
- 抽样误差
- 因未调查全部单位产生的误差
控制策略
- 非抽样误差:问卷预测试、调查员培训、自动化数据处理
- 抽样误差:增加样本量或改进抽样设计
四、抽样方法详解
1. 简单随机抽样(SRS)(7.4节)
定义
每个容量为 n n n的样本被抽中的概率相同,样本独立无关联
抽样步骤
- 建立抽样框(总体所有个体名册)
- 使用随机数表抽取样本
参数估计公式
-
总体均值 μ \mu μ
x ˉ ± z α / 2 ⋅ s n 1 − n N \bar{x} \pm z_{\alpha/2} \cdot \frac{s}{\sqrt{n}} \sqrt{1 - \frac{n}{N}} xˉ±zα/2⋅ns1−Nn
使用条件:- n ≥ 30 n \geq 30 n≥30(中心极限定理)
- n / N > 5 % n/N > 5\% n/N>5%时必须使用有限总体修正系数
-
总体比率 p p p
p ^ ± z α / 2 ⋅ p ^ ( 1 − p ^ ) n 1 − n N \hat{p} \pm z_{\alpha/2} \cdot \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \sqrt{1 - \frac{n}{N}} p^±zα/2⋅np^(1−p^)1−Nn
使用条件: n p ^ ≥ 5 n\hat{p} \geq 5 np^≥5 且 n ( 1 − p ^ ) ≥ 5 n(1-\hat{p}) \geq 5 n(1−p^)≥5
样本容量确定
- 估计均值:
n = N ⋅ z α / 2 2 ⋅ s 2 ( N − 1 ) B 2 + z α / 2 2 s 2 n = \frac{N \cdot z_{\alpha/2}^2 \cdot s^2}{(N-1)B^2 + z_{\alpha/2}^2 s^2} n=(N−1)B2+zα/22s2N⋅zα/22⋅s2 - 估计比率:
n = N ⋅ z α / 2 2 ⋅ p ( 1 − p ) ( N − 1 ) B 2 + z α / 2 2 p ( 1 − p ) n = \frac{N \cdot z_{\alpha/2}^2 \cdot p(1-p)}{(N-1)B^2 + z_{\alpha/2}^2 p(1-p)} n=(N−1)B2+zα/22p(1−p)N⋅zα/22⋅p(1−p)
关键参数:- B B B:允许误差(置信区间半宽)
- s 2 s^2 s2或 p p p:需预先估计(历史数据/预抽样)
- p p p未知时用 p = 0.5 p=0.5 p=0.5保守估计
案例示范
-
例7.1(杂志订户收入估计):
N = 8000 , n = 484 , x ˉ = 30500 , s = 7040 N=8000,\ n=484,\ \bar{x}=30500,\ s=7040 N=8000, n=484, xˉ=30500, s=7040
95 % C I : 30500 ± 1.96 × 7040 484 × 1 − 484 8000 → [ 29880 , 31120 ] 95\%\ CI:\ 30500 \pm 1.96 \times \frac{7040}{\sqrt{484}} \times \sqrt{1-\frac{484}{8000}} \rightarrow [29880,\ 31120] 95% CI: 30500±1.96×4847040×1−8000484→[29880, 31120] -
例7.3(毕业生收入调查样本量):
要求: B = 500 , N = 5000 , s = 3000 B=500,\ N=5000,\ s=3000 B=500, N=5000, s=3000
n = 5000 × 1.96 2 × 3000 2 4999 × 500 2 + 1.96 2 × 3000 2 ≈ 139 n = \frac{5000 \times 1.96^2 \times 3000^2}{4999 \times 500^2 + 1.96^2 \times 3000^2} \approx 139 n=4999×5002+1.962×300025000×1.962×30002≈139
2. 分层简单随机抽样(7.5节)
适用场景
总体存在异质子群(如不同专业、地区),层内差异小、层间差异大
抽样步骤
- 将总体划分为 H H H层
- 每层独立抽取简单随机样本
- 按层权加权合并结果
参数估计
-
总体均值:
x ˉ s t r = ∑ h = 1 H ( N h N ) x ˉ h \bar{x}_{str} = \sum_{h=1}^{H} \left( \frac{N_h}{N} \right) \bar{x}_h xˉstr=∑h=1H(NNh)xˉh
标准误:
s x ˉ s t r = ∑ h = 1 H ( N h N ) 2 s h 2 n h ( 1 − n h N h ) s_{\bar{x}_{str}} = \sqrt{ \sum_{h=1}^{H} \left( \frac{N_h}{N} \right)^2 \frac{s_h^2}{n_h} \left(1 - \frac{n_h}{N_h}\right) } sxˉstr=∑h=1H(NNh)2nhsh2(1−Nhnh)
置信区间: x ˉ s t r ± 1.96 s x ˉ s t r \bar{x}_{str} \pm 1.96 s_{\bar{x}_{str}} xˉstr±1.96sxˉstr -
总体比率:
p ^ s t r = ∑ h = 1 H ( N h N ) p ^ h \hat{p}_{str} = \sum_{h=1}^{H} \left( \frac{N_h}{N} \right) \hat{p}_h p^str=∑h=1H(NNh)p^h
标准误:
s p ^ s t r = ∑ h = 1 H ( N h N ) 2 p ^ h ( 1 − p ^ h ) n h ( 1 − n h N h ) s_{\hat{p}_{str}} = \sqrt{ \sum_{h=1}^{H} \left( \frac{N_h}{N} \right)^2 \frac{\hat{p}_h(1-\hat{p}_h)}{n_h} \left(1 - \frac{n_h}{N_h}\right) } sp^str=∑h=1H(NNh)2nhp^h(1−p^h)(1−Nhnh)
样本分配
- 比例分配: n h = n × N h N n_h = n \times \frac{N_h}{N} nh=n×NNh
- 最优分配(Neyman)(各层成本相同时):
n h = n ⋅ N h s h ∑ h = 1 H N h s h n_h = n \cdot \frac{N_h s_h}{\sum_{h=1}^H N_h s_h} nh=n⋅∑h=1HNhshNhsh
案例示范
- 例7.4(管理学院毕业生收入分层估计):
结果: x ˉ s t r = 29350 , s x ˉ s t r = 281.6 → 95 % C I [ 29074 , 29626 ] \bar{x}_{str} = 29350,\ s_{\bar{x}_{str}} = 281.6 \rightarrow 95\%\ CI[29074,\ 29626] xˉstr=29350, sxˉstr=281.6→95% CI[29074, 29626] - 例7.5(年薪≥36000元比率估计):
p ^ s t r = 0.0981 → 95 % C I [ 0.0575 , 0.1387 ] \hat{p}_{str} = 0.0981 \rightarrow 95\%\ CI[0.0575,\ 0.1387] p^str=0.0981→95% CI[0.0575, 0.1387]
3. 整群抽样(7.6节)
适用场景
总体天然分群(如学校、村庄),群内差异大、群间差异小
参数估计
-
总体均值:
x ˉ c l s = ∑ i = 1 n x i ∑ i = 1 n M i \bar{x}_{cls} = \frac{\sum_{i=1}^{n} x_i}{\sum_{i=1}^{n} M_i} xˉcls=∑i=1nMi∑i=1nxi( x i x_i xi:第 i i i群观测值总和)
标准误:
s x ˉ c l s = 1 M ˉ 2 ⋅ s r 2 n ( 1 − n N ) s_{\bar{x}_{cls}} = \sqrt{ \frac{1}{\bar{M}^2} \cdot \frac{s_r^2}{n} \left(1 - \frac{n}{N}\right) } sxˉcls=Mˉ21⋅nsr2(1−Nn)
其中:
s r 2 = ∑ i = 1 n ( x i − x ˉ c l s M i ) 2 n − 1 , M ˉ = ∑ M i n s_r^2 = \frac{\sum_{i=1}^{n} (x_i - \bar{x}_{cls} M_i)^2}{n-1},\quad \bar{M} = \frac{\sum M_i}{n} sr2=n−1∑i=1n(xi−xˉclsMi)2,Mˉ=n∑Mi -
总体比率:
p ^ c l s = ∑ i = 1 n a i ∑ i = 1 n M i \hat{p}_{cls} = \frac{\sum_{i=1}^{n} a_i}{\sum_{i=1}^{n} M_i} p^cls=∑i=1nMi∑i=1nai( a i a_i ai:第 i i i群具有特征的数量)
案例示范(例7.6)
- 注册会计师年薪估计:
x ˉ c l s = 42531 元 , s x ˉ c l s = 1.730 → 95 % C I [ 39071 , 45991 ] \bar{x}_{cls} = 42531\text{元},\ s_{\bar{x}_{cls}} = 1.730 \rightarrow 95\%\ CI[39071,\ 45991] xˉcls=42531元, sxˉcls=1.730→95% CI[39071, 45991] - 女性比率估计:
p ^ c l s = 0.2734 → 95 % C I [ 0.2052 , 0.3416 ] \hat{p}_{cls} = 0.2734 \rightarrow 95\%\ CI[0.2052,\ 0.3416] p^cls=0.2734→95% CI[0.2052, 0.3416]
4. 系统抽样(7.7节)
方法
固定间隔 k k k抽样(首个单位随机起点)
使用条件
抽样框随机排列(否则有周期性偏差风险)
优缺点
| 优点 | 缺点 |
|---|---|
| 操作简便 | 若抽样框存在隐周期性,样本可能有偏 |
| 成本低 |
五、样本容量确定通法
- 规定精度 B B B和置信水平
- 选择抽样方法
- 若有历史数据,用其估计方差 s 2 s^2 s2或 p p p
- 若无历史数据,进行预抽样估计方差
- 代入公式计算 n n n
- 验证实际精度
特殊情形处理:
- 分层抽样:先分配样本再计算总样本量
- 整群抽样:需预先估计群间方差 s r 2 s_r^2 sr2
六、解题步骤模板
1. 简单随机抽样(均值估计)
- 确认抽样框和 N N N
- 抽取 n ≥ 30 n \geq 30 n≥30的样本
- 计算 x ˉ \bar{x} xˉ和 s s s
- 计算标准误: s e = s n × 1 − n N se = \frac{s}{\sqrt{n}} \times \sqrt{1-\frac{n}{N}} se=ns×1−Nn
- 确定 z z z值(95%CI取1.96)
- 计算CI: x ˉ ± z ⋅ s e \bar{x} \pm z \cdot se xˉ±z⋅se
2. 分层抽样(比率估计)
- 按特征分层
- 确定各层权 W h = N h / N W_h = N_h/N Wh=Nh/N
- 按比例分配样本 n h n_h nh
- 各层计算 p ^ h \hat{p}_h p^h
- 计算加权估计 p ^ s t r = ∑ W h p ^ h \hat{p}_{str} = \sum W_h \hat{p}_h p^str=∑Whp^h
- 计算标准误 s p ^ s t r s_{\hat{p}_{str}} sp^str
- 构造CI: p ^ s t r ± 1.96 ⋅ s p ^ s t r \hat{p}_{str} \pm 1.96 \cdot s_{\hat{p}_{str}} p^str±1.96⋅sp^str
3. 样本量计算题
- 读取 N , B , N, B, N,B,置信水平
- 选择参数类型(均值/比率)
- 若估计均值,查找 s 2 s^2 s2历史值
- 若估计比率,采用 p = 0.5 p=0.5 p=0.5或历史值
- 代入公式求解 n n n
- 若 n / N > 5 % n/N > 5\% n/N>5%,使用有限总体修正
七、易错点警示
-
抽样框陷阱
- 目标总体 ≠ 抽样总体 → 推断结论有偏差
- 例:用电话簿抽样框调查网民会遗漏无固话群体
-
中心极限定理误用
- n < 30 n<30 n<30时不可直接使用 z z z值(需查 t t t分布表)
- 偏态总体需 n ≥ 50 n \geq 50 n≥50才近似正态
-
有限总体修正遗漏
- 当 n / N > 5 % n/N>5\% n/N>5%时未使用修正系数 → 标准误高估
-
整群抽样加权缺失
- 群大小不等时未用加权均值 → 估计有偏
- 例7.6必须用总年薪/总人数而非群均值的平均
-
分层抽样分配误区
- 最优分配需已知层标准差 s h s_h sh → 若无数据应先比例分配
相关文章:
——统计抽样学习笔记(考试用))
统计学(第8版)——统计抽样学习笔记(考试用)
一、统计抽样的核心内容与问题 研究内容 从总体中科学抽取样本的方法利用样本数据推断总体特征(均值、比率、总量)控制抽样误差与非抽样误差 解决的核心问题 在成本约束下,用少量样本准确推断总体特征量化估计结果的可靠性(置…...
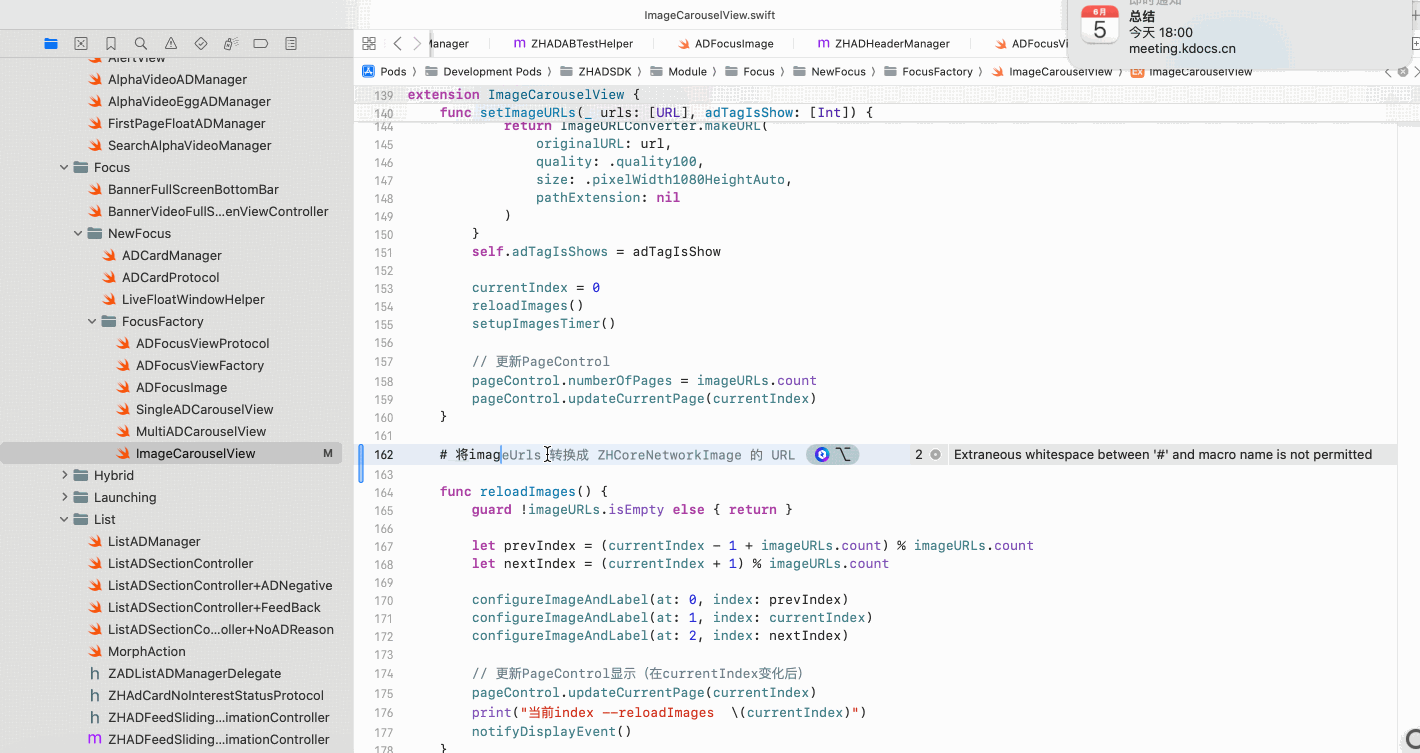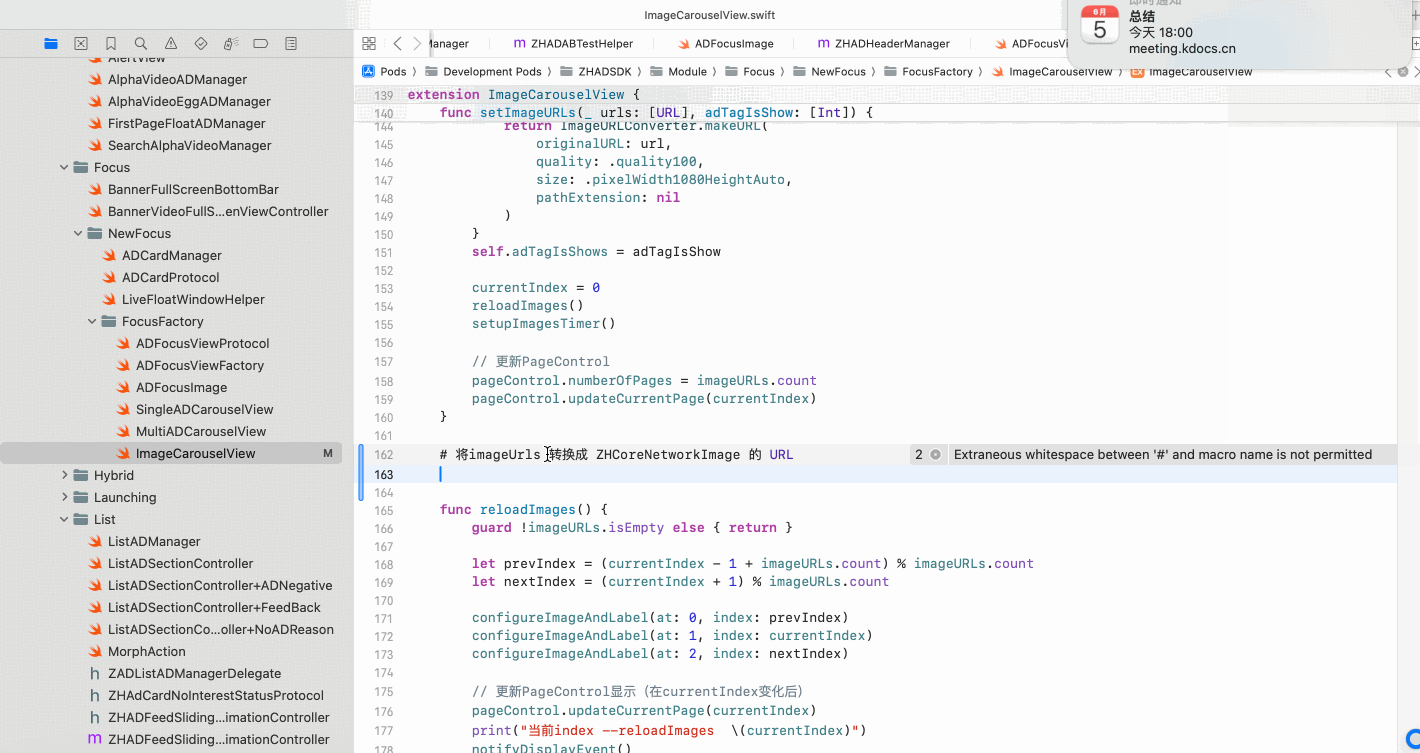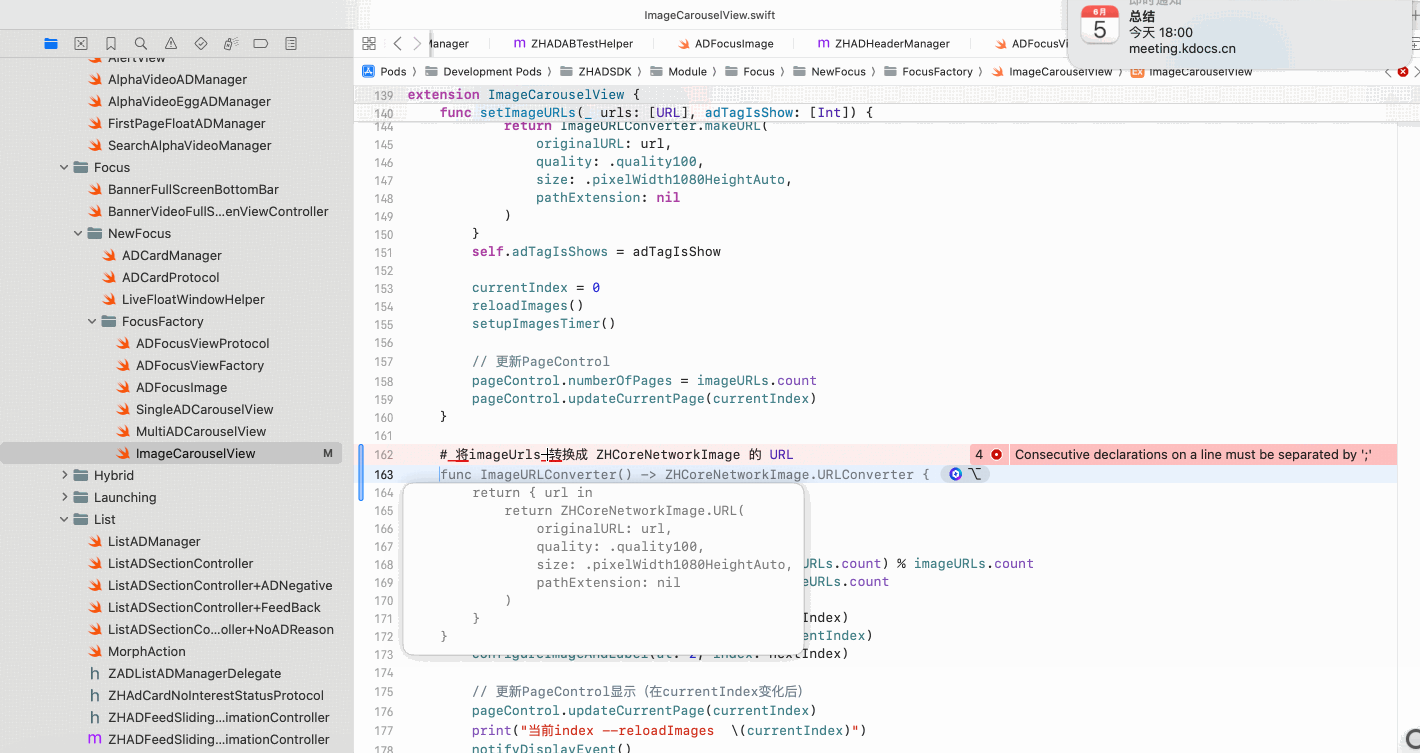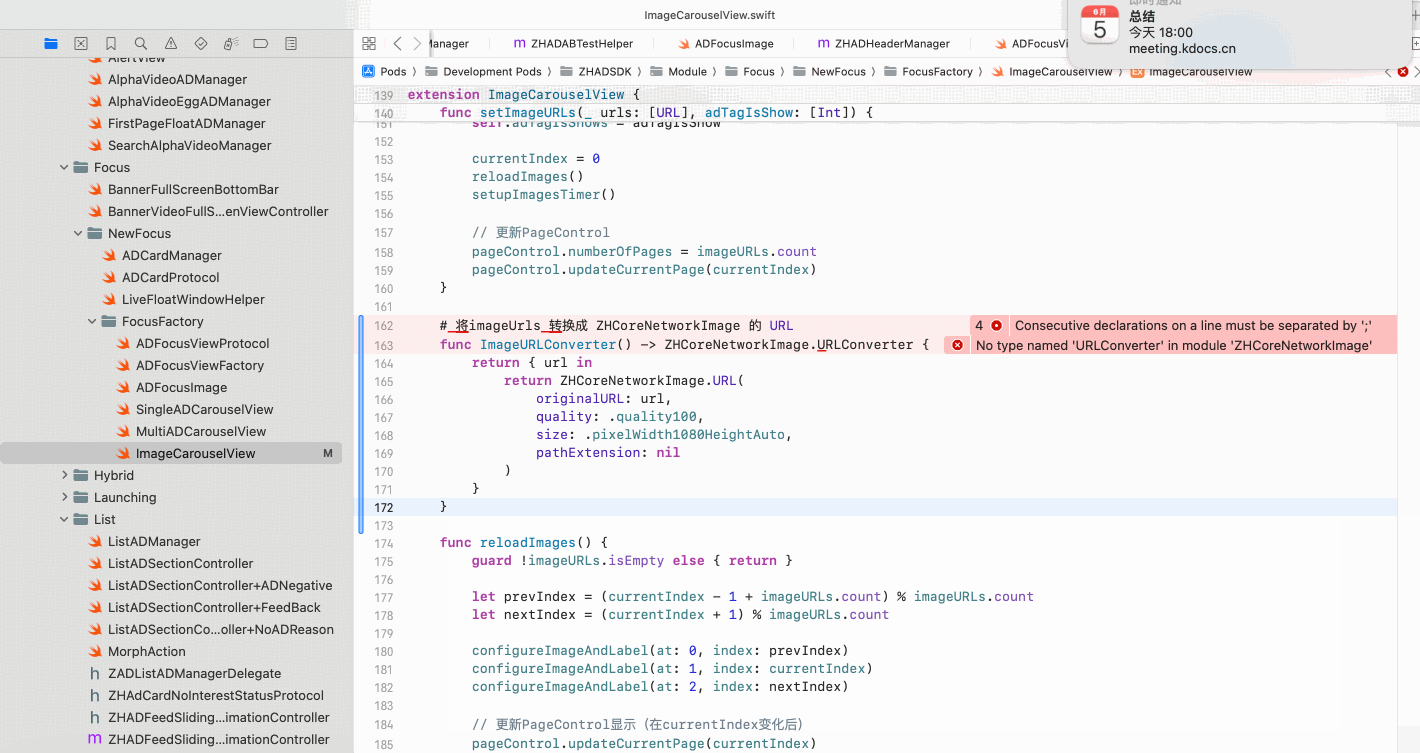
Copilot for Xcode (iOS的 AI辅助编程)
Copilot for Xcode 简介Copilot下载与安装 体验环境要求下载最新的安装包安装登录系统权限设置 AI辅助编程生成注释代码补全简单需求代码生成辅助编程行间代码生成注释联想 代码生成 总结 简介 尝试使用了Copilot,它能根据上下文补全代码,快速生成常用…...
Axure零基础跟我学:展开与收回
亲爱的小伙伴,如有帮助请订阅专栏!跟着老师每课一练,系统学习Axure交互设计课程! Axure产品经理精品视频课https://edu.csdn.net/course/detail/40420 课程主题:Axure菜单展开与收回 课程视频:...

Docker、Wsl 打包迁移环境
电脑需要开启wsl2 可以使用wsl -v 查看当前的版本 wsl -v WSL 版本: 2.2.4.0 内核版本: 5.15.153.1-2 WSLg 版本: 1.0.61 MSRDC 版本: 1.2.5326 Direct3D 版本: 1.611.1-81528511 DXCore 版本: 10.0.2609…...

RabbitMQ 各类交换机
为什么要用交换机? 交换机用来路由消息。如果直发队列,这个消息就被处理消失了,那别的队列也需要这个消息怎么办?那就要用到交换机 交换机类型 1,fanout:广播 特点 广播所有消息:将消息…...

高保真组件库:开关
一:制作关状态 拖入一个矩形作为关闭的底色:44 x 22,填充灰色CCCCCC,圆角23,边框宽度0,文本为”关“,右对齐,边距2,2,6,2,文本颜色白色FFFFFF。 拖拽一个椭圆,尺寸18 x 18,边框为0。3. 全选转为动态面板状态1命名为”关“。 二:制作开状态 复制关状态并命名为”开…...
未授权访问事件频发,我们应当如何应对?
在当下,数据已成为企业和组织的核心资产,是推动业务发展、决策制定以及创新的关键驱动力。然而,未授权访问这一隐匿的安全威胁,正如同高悬的达摩克利斯之剑,时刻威胁着数据的安全,一旦触发,便可…...

Easy Excel
Easy Excel 一、依赖引入二、基本使用1. 定义实体类(导入/导出共用)2. 写 Excel3. 读 Excel 三、常用注解说明(完整列表)四、进阶:自定义转换器(Converter) 其它自定义转换器没生效 Easy Excel在…...

欢乐熊大话蓝牙知识17:多连接 BLE 怎么设计服务不会乱?分层思维来救场!
多连接 BLE 怎么设计服务不会乱?分层思维来救场! 作者按: 你是不是也遇到过 BLE 多连接时,调试现场像网吧“掉线风暴”? 温度传感器连上了,心率带丢了;一边 OTA 更新,一边通知卡壳。…...

AWS vs 阿里云:功能、服务与性能对比指南
在云计算领域,Amazon Web Services (AWS) 和阿里云 (Alibaba Cloud) 是全球领先的提供商,各自在功能范围、服务生态系统、性能表现和适用场景上具有独特优势。基于提供的引用[1]-[5],我将从功能、服务和性能三个方面进行结构化对比分析&#…...

用js实现常见排序算法
以下是几种常见排序算法的 JS实现,包括选择排序、冒泡排序、插入排序、快速排序和归并排序,以及每种算法的特点和复杂度分析 1. 选择排序(Selection Sort) 核心思想:每次从未排序部分选择最小元素,与未排…...

python读取SQLite表个并生成pdf文件
代码用于创建含50列的SQLite数据库并插入500行随机浮点数据,随后读取数据,通过ReportLab生成横向PDF表格,包含格式化(两位小数)及表头、网格线等美观样式。 # 导入所需库 import sqlite3 # 用于操作…...

当下AI智能硬件方案浅谈
背景: 现在大模型出来以后,打破了常规的机械式的对话,人机对话变得更聪明一点。 对话用到的技术主要是实时音视频,简称为RTC。下游硬件厂商一般都不会去自己开发音视频技术,开发自己的大模型。商用方案多见为字节、百…...

大模型真的像人一样“思考”和“理解”吗?
Yann LeCun 新研究的核心探讨:大语言模型(LLM)的“理解”和“思考”方式与人类认知的根本差异。 核心问题:大模型真的像人一样“思考”和“理解”吗? 人类的思考方式: 你的大脑是个超级整理师。面对海量信…...

【题解-洛谷】P10480 可达性统计
题目:P10480 可达性统计 题目描述 给定一张 N N N 个点 M M M 条边的有向无环图,分别统计从每个点出发能够到达的点的数量。 输入格式 第一行两个整数 N , M N,M N,M,接下来 M M M 行每行两个整数 x , y x,y x,y,表示从 …...

在Spring Boot中集成RabbitMQ的完整指南
前言 在现代微服务架构中,消息队列(Message Queue)是实现异步通信、解耦系统组件的重要工具。RabbitMQ 是一个流行的消息中间件,支持多种消息协议,具有高可靠性和可扩展性。 本博客将详细介绍如何在 Spring Boot 项目…...
Element-Plus:popconfirm与tooltip一起使用不生效?
你们好,我是金金金。 场景 我正在使用Element-plus组件库当中的el-popconfirm和el-tooltip,产品要求是两个需要结合一起使用,也就是鼠标悬浮上去有提示文字,并且点击之后需要出现气泡确认框 代码 <el-popconfirm title"是…...

Selenium 查找页面元素的方式
Selenium 查找页面元素的方式 Selenium 提供了多种方法来查找网页中的元素,以下是主要的定位方式: 基本定位方式 通过ID定位 driver.find_element(By.ID, "element_id")通过Name定位 driver.find_element(By.NAME, "element_name"…...
OPENCV图形计算面积、弧长API讲解(1)
一.OPENCV图形面积、弧长计算的API介绍 之前我们已经把图形轮廓的检测、画框等功能讲解了一遍。那今天我们主要结合轮廓检测的API去计算图形的面积,这些面积可以是矩形、圆形等等。图形面积计算和弧长计算常用于车辆识别、桥梁识别等重要功能,常用的API…...

【Java】Ajax 技术详解
文章目录 1. Filter 过滤器1.1 Filter 概述1.2 Filter 快速入门开发步骤:1.3 Filter 执行流程1.4 Filter 拦截路径配置1.5 过滤器链2. Listener 监听器2.1 Listener 概述2.2 ServletContextListener3. Ajax 技术3.1 Ajax 概述3.2 Ajax 快速入门服务端实现:客户端实现:4. Axi…...

spring boot使用HttpServletResponse实现sse后端流式输出消息
1.以前只是看过SSE的相关文章,没有具体实践,这次接入AI大模型使用到了流式输出,涉及到给前端流式返回,所以记录一下。 2.resp要设置为text/event-stream resp.setContentType("text/event-stream"); resp.setCharacter…...

二叉树-144.二叉树的前序遍历-力扣(LeetCode)
一、题目解析 对于递归方法的前序遍历十分简单,但对于一位合格的程序猿而言,需要掌握将递归转化为非递归的能力,毕竟递归调用的时候会调用大量的栈帧,存在栈溢出风险。 二、算法原理 递归调用本质是系统建立栈帧,而非…...

无需布线的革命:电力载波技术赋能楼宇自控系统-亚川科技
无需布线的革命:电力载波技术赋能楼宇自控系统 在楼宇自动化领域,传统控制系统依赖复杂的专用通信线路,不仅施工成本高昂,后期维护和扩展也极为不便。电力载波技术(PLC)的突破性应用,彻底改变了…...

Netty自定义协议解析
目录 自定义协议设计 实现消息解码器 实现消息编码器 自定义消息对象 配置ChannelPipeline Netty提供了强大的编解码器抽象基类,这些基类能够帮助开发者快速实现自定义协议的解析。 自定义协议设计 在实现自定义协议解析之前,需要明确协议的具体格式。例如,一个简单的…...

__VUE_PROD_HYDRATION_MISMATCH_DETAILS__ is not explicitly defined.
这个警告表明您在使用Vue的esm-bundler构建版本时,未明确定义编译时特性标志。以下是详细解释和解决方案: 问题原因: 该标志是Vue 3.4引入的编译时特性标志,用于控制生产环境下SSR水合不匹配错误的详细报告1使用esm-bundler…...
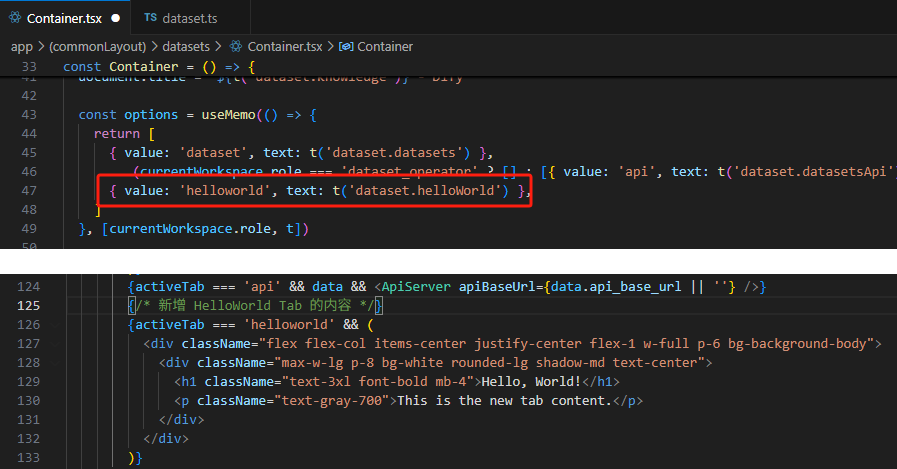
【技巧】dify前端源代码修改第一弹-增加tab页
回到目录 【技巧】dify前端源代码修改第一弹-增加tab页 尝试修改dify的前端源代码,在知识库增加一个tab页"HELLO WORLD",完成后的效果如下 [gif01] 1. 前端代码进入调试模式 参考 【部署】win10的wsl环境下启动dify的web前端服务 启动调试…...

Java设计模式:责任链模式
一、什么是责任链模式? 责任链模式(Chain of Responsibility Pattern) 是一种 行为型设计模式,它通过将请求沿着一条处理链传递,直到某个对象处理它为止。这种模式的核心思想是 解耦请求的发送者和接收者,…...

比特币:固若金汤的数字堡垒与它的四道防线
第一道防线:机密信函——无法破解的哈希加密 将每一笔比特币交易比作一封在堡垒内部传递的机密信函。 解释“哈希”(Hashing)就是一种军事级的加密术(SHA-256),能将信函内容(交易细节…...

基于 HTTP 的单向流式通信协议SSE详解
SSE(Server-Sent Events)详解 🧠 什么是 SSE? SSE(Server-Sent Events) 是 HTML5 标准中定义的一种通信机制,它允许服务器主动将事件推送给客户端(浏览器)。与传统的 H…...

初探用uniapp写微信小程序遇到的问题及解决(vue3+ts)
零、关于开发思路 (一)拿到工作任务,先理清楚需求 1.逻辑部分 不放过原型里说的每一句话,有疑惑的部分该问产品/测试/之前的开发就问 2.页面部分(含国际化) 整体看过需要开发页面的原型后,分类一下哪些组件/样式可以复用,直接提取出来使用 (时间充分的前提下,不…...
